基于贝叶斯信念网络的新生高考成绩分析

朱贺

摘要： 学生最关心的问题莫过于考试成绩和名次，但面对纷繁的科目和有限时间的矛盾，学生很难在短时间内将各个成绩都有一个明显的提高。选择哪一门努力突击，提高单门成绩，就成为困扰学生的难题。贝叶斯信念网络在复杂的存在不确定性和关联性的问题上有着很好适应性，适用于此问题的探索。通过某校2014年理科录取新生高考各门成绩的分析，以贝叶斯信念网络为模型基础，旨在为高考学生提供科目选择的参考。

关键词：贝叶斯信念网络；成绩分析；高考

中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2015）08-0261-02

现代社会是一个讲求效率的社会，在学习上同样也是这样。学生试图以最小的时间耗费获得最大的效益，也就是成绩的提高。但面对纷繁的科目和有限时间的矛盾，想要在短时间内获得各科成绩的提高又似乎是一件不可能完成的任务。由此，产生了一个历年来困扰学生的问题，在有限的时间内学习哪一门才能获得最大的名次提升，提高在录取时的竞争力。本文借助贝叶斯网络模型，通过对某高校2014年理科录取新生成绩的研究，得到了一些启示。

1贝叶斯信念网络概述

贝叶斯信念网络，是Pearl在1988年提出的，是贝叶斯方法的推进，能有效的处理多源信息的表达，在知识的分析及推理领域有着广泛的应用。贝叶斯网络模型是一种概率网络模型，其使用图形化网格来做概率推理，以获得概率信息，适合应用在复杂的存在不确定性和关联性的问题上。

贝叶斯网络可由两种元素解释：有向无环图和条件概率表（CPT）。通过有向边链接各种变量节点，构成有向无环图。在有向无环图中，每个节点为一种随机变量，而每条有向边体现出节点间的依赖关系，有向边的箭头指向子节点。而这种依赖关系的强弱的具体体现就通过条件概率表显示出来。

贝叶斯网络构造可按以下方法进行。

（1） 收集相关变量，明确其意义：确定目标变量，寻找和目标变量相关的其观测变量，并穷尽变量值以构造模型。

（2） 建立有向无环图：

（3） 确定局部概率[pxipai]，为每一个变量[xi]的父节点集合确定所有分布。

2构建以高考成绩为数据集的贝叶斯信念网络

2.1 模型构建

选取某高校2014年理科录取学生成绩，保留录取志愿及高考分数字段，删除其他字段。以学生填报的志愿为目标变量，并将该校的18个理科录取专业数据映射为“0-17”18个数字字段，理科综合、英语、数学、语文四门高考科目为预测变量，通过IBM SPSS Modeler15.0软件建立贝叶斯网络。贝叶斯网络的结构类型使用TAN算法，参数学习方法使用最大似然法。数据甄别使用数据审核模块，模型构建评价使用ROC評估模块，最终构建模型如图1所示。

2.2 实验结果及分析

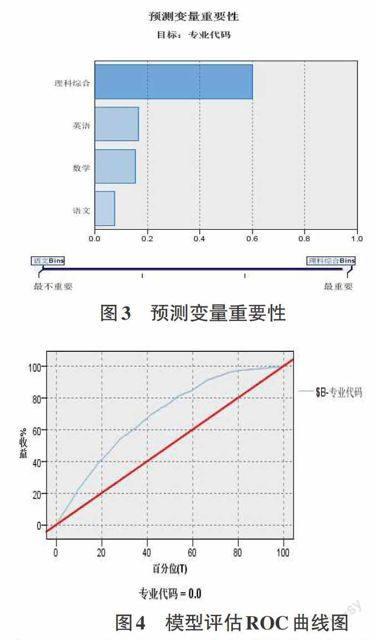
通过贝叶斯信念网络模型，使用高考各科成绩数据，最终构造出的有向无环图如图2所示。各变量重要性经过标准化处理后，理科综合、英语、数学、语文四个变量重要性分别为0.6、017、0.16、0.08，如图3所示，成绩数据分类录取志愿的收益ROC图，如图4所示。

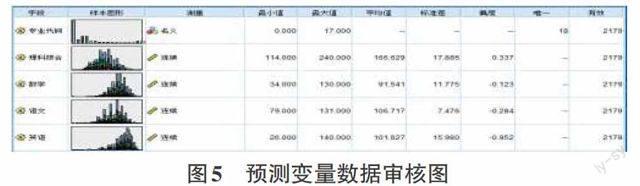
通过收益ROC图，可以看出专业代码为“0”的收益曲线比收益基准线有了明显的提高，其下方面积也较收益基准线下方的面积有了明显的增大，代表此分类模型的准确率是可观的并可以作为参考的。在此基础上，透过变量重要性图，得出理科综合变量的重要性显著的高于其他三个变量，即意味着该变量在决定最终目标变量的分类中具有最大的权重。同时，如图5所示，理科综合标准差是最大的，代表其数据分布距均值的距离较大；而且数据分布较其他变量而言，范围较广，具有相同值的数据较少，数据体现出分类的区别度更高。

3总结

以贝叶斯信念网络为模型，拟合某高校2014级新生高考成绩数据，得到的结果显示出理科综合在录取专业的分类中具有最重要的地位，决定着专业录取类别。虽然各单科成绩的提高都会在最终总分上得以体现，但是从以上分析可以看出，不同于理科综合科目，其他三门科目的考生成绩分布较集中，体现出题目的难易度在考生上有了较为相似的反应，在分数上就是考生分数较为集中，高低分差距不大。反观理科综合科目，考生分数分布较为分散，题目难易度体现在考生上有了较大的反差，分数有较大的区分度，高低分差距明显。这样，我们得到结论：以此高校新生高考数据而言，如果考生将精力多用于理科综合的学习，提高该门科目的成绩，其在专业选择上就会有较大的优势。

参考文献：

[1] 谢斌，刘长建.基于贝叶斯网络构建的学生成绩评价系统及影响分析[J].中国科教创新导刊，2011（31）：34-35.

[1] 姜红艳.数据挖掘在学生成绩分析中的应用[D].吉林大学，2006.

[2] 丁知斌，袁方.基于数据仓库的数据挖掘技术在高校学生成绩分析中的应用[J].河北大学成人教育学院学报，2004（4）：19-21.

[3] 黄羿，马新强，武彤，等.基于数据仓库的学生成绩分析模型设计[J].信息技术，2007（2）：18-20.

[4] 周建方，唐椿炎，许智勇.事件树、故障树、决策树与贝叶斯网络[J].河海大学学报：自然科学版，2009（3）：351-355.

[5] 张少中.基于贝叶斯网络的知识发现与决策应用研究[D].大连理工大学，2003.

[6] 姚武军，魏彬.基于贝叶斯树和集成学习的异常检测[J].武汉大学学报：理学版，2014（6）：497-499.

[7] 慕春棣，戴剑彬，叶俊.用于数据挖掘的贝叶斯网络[J].软件学报，2000（5）：660-666.

[8] 胡春玲.贝叶斯网络研究综述[J].合肥学院学报：自然科学版，2013（1）：33-39.

[9] 王国平，郭伟宸，汪若君.IBM SPSS Modeler数据与文本挖掘实战[M].清华大学出版社，2014.

[10] 范明，孟小峰（译）.数据挖掘概念与技术（原书第三版）[M].机械工业出版社，2012.