微压痕仪的刚度标定

官春平

（广东轻工职业技术学院，广东广州 510300）

目前，测试纳米材料、薄膜及表面涂层等微小体积材料的弹性模量和硬度等力学性能参数的方法主要是纳米压痕法。其原理是通过采集压头压入材料的过程中，连续记录试验中的载荷—位移曲线，然后通过该曲线来计算材料的弹性模量和硬度等参数。为了获得准确的载荷—位移曲线，一方面采用高精度的载荷、位移传感器，另一方面必须对压痕仪的加载系统的刚度进行标定，并将其产生的位移分量从测得的总位移中去除掉，从而获得高精度的压头位移量。因此压痕仪的刚度标定是压痕法测试的一项重要工作，是保证仪器测试精度的必要手段[1]。本文在对广泛使用于纳米压痕法的Oliver-Pharr[2]模型进行分析的基础上，通过压痕试验，完成压痕仪的刚度标定。

1 Oliver-Pharr压痕测试原理

20世纪90年代发展起来的压痕技术，现已广泛应用于微纳材料及涂层材料的弹性模量、硬度、硬化指数、残余应力和断裂强度等力学性能的测量。压痕仪的工作原理简图如图1所示。

外部载荷F通过加载机构将力施加于压头上，经过压头与被测材料的接触，实现被测材料的局部弹塑性变形。图1中的K1代表加载机构的刚度，K2代表压头与被测材料的刚度，h为压头的位移量。

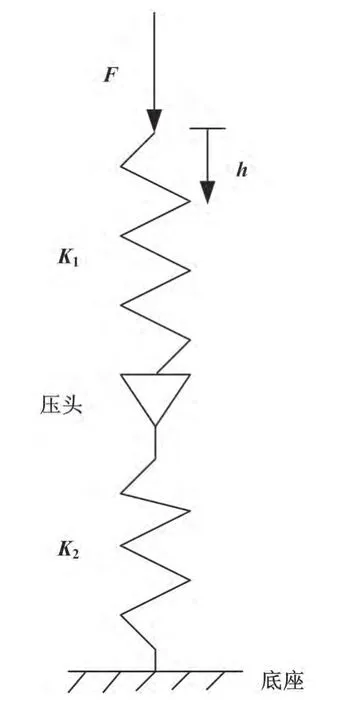
图1 压痕仪的工作原理简图

目 前 ， Oli⁃ver-Pharr压痕测试方法在商用的纳米压痕仪上得到广泛应用。其通过精确测量压头在加载、卸载过程中的载荷—位移曲线，计算其接触深度hc、初始卸载斜率S、最大载荷Fm、最大加载深度hm等来计算被测材料的弹性模量E和硬度H。其计算公式为：

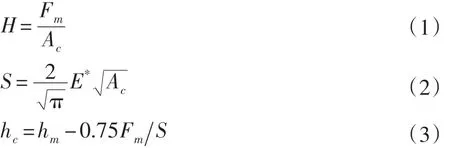
其中：Ac为接触面积，对于洛氏尖压头：

E*是等效弹性模量，其计算公式为：

其中：Ei、vi为压头材料的弹性模量和泊松比，E、v为被压材料的弹性模量和泊松比。

从式（1）～（4）中可以看出，压痕深度的测量精度对于压痕仪的测量结果有着至关重要的影响。而压痕深度的精度除了与位移传感器的精度有关外，还受到加载机构刚度的影响。

2 刚度测试方法

从图1中可以看出，由于加载机构在试验过程中会发生弹性变形，导致实际测量的位移值中增加了加载机构的变形。图2反映了加载机构的刚度对压痕过程中的载荷—位移曲线的影响示意图。随着加载载荷的增加，实际测量的位移值逐渐大于实际材料的压痕深度，在最大载荷Fm时，其实际测量的位移值比材料的实际压痕深度增大了△h，可见系统的总刚度降低了。

假定系统的总刚度为K，则：

为了方便计算，定义系统的柔度为C，且C=1/K。则系统总的柔度为：C=C1+C2，其中C1为加载机构的柔度，C1=1/K1，C2为压头与试样的接触柔度，C2=1/S。

根据式（2）可知：

因此，系统的总柔度C为：

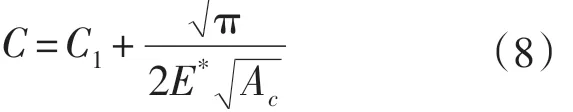
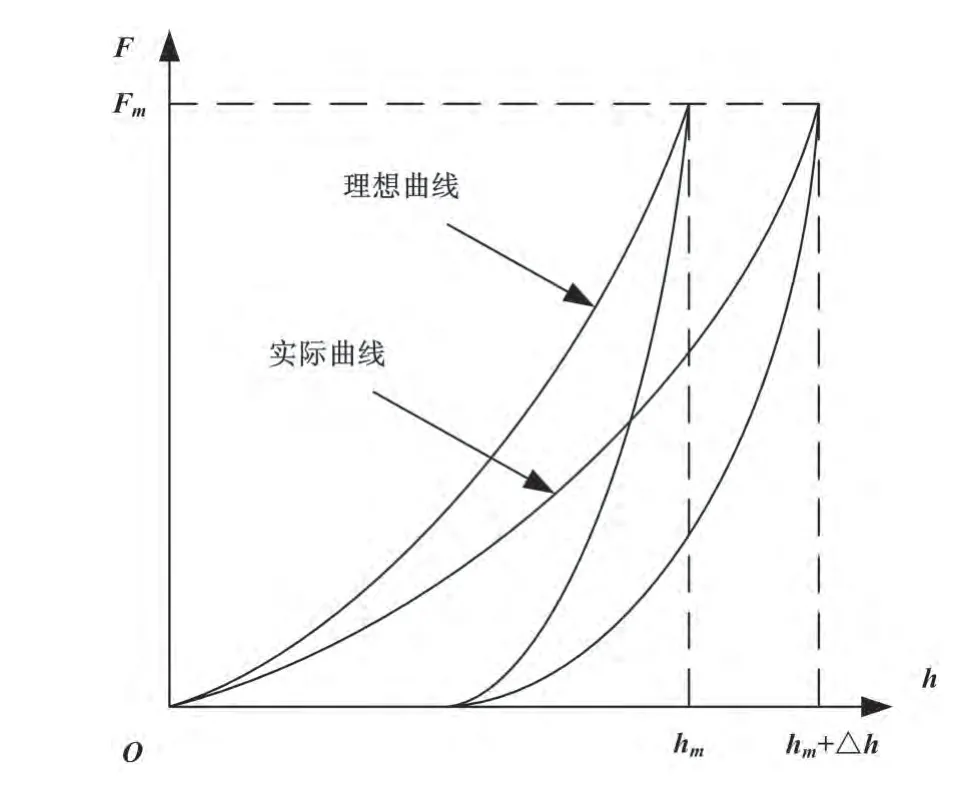
图2 加载机构的刚度对载荷—位移的影响

根据式（1）可知，Ac=Fm/H，将该式带入到式（8）中，有：

对于给定的某种被压材料，其硬度值和减缩模量为一定值。而加载系统的变形处于弹性变形，即其柔度为一定值。因此，从式（9）中可以看出，系统的总柔度成线性关系。如果对某一种材料进行不同载荷下的压痕试验，测量试验过程中的载荷—位移曲线，即可获得系统的总柔度的关系曲线，通过对该曲线进行线性拟合，即可得到加载机构的刚度。

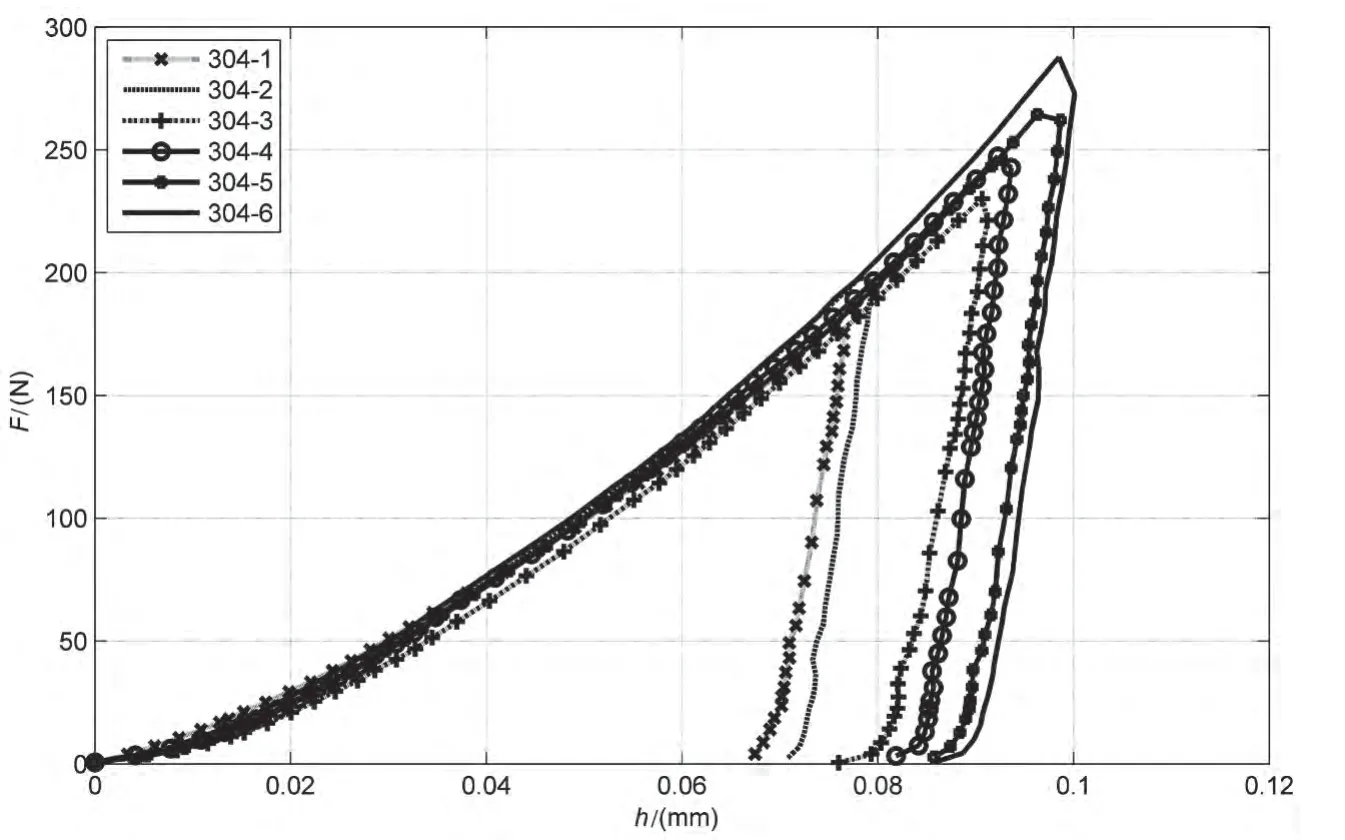
图3 压痕试验的载荷—位移曲线

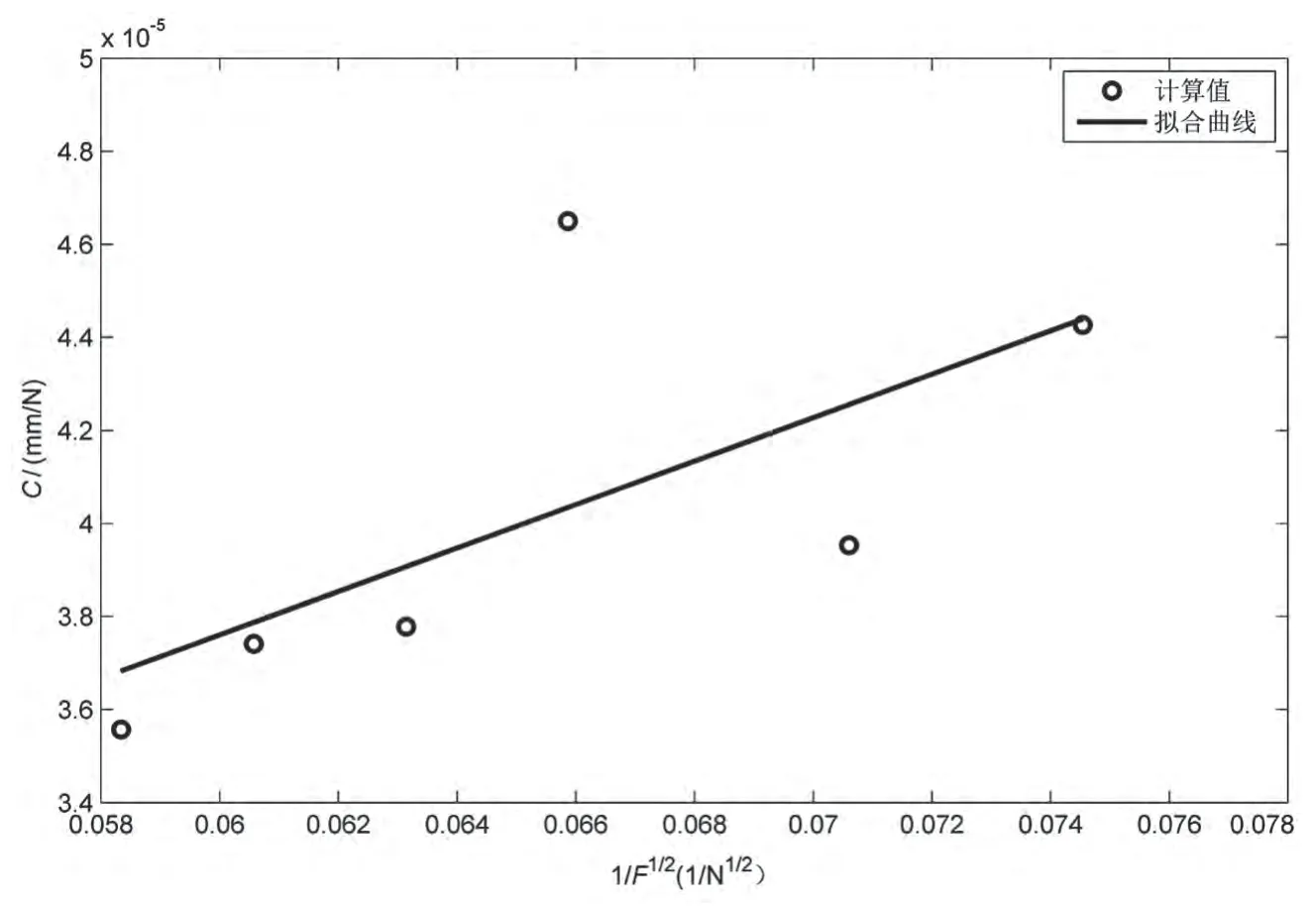
图4 系统总柔度C与1的关系曲线

3 压痕实验及刚度计算

压痕试验所采用的测试材料为304不锈钢，在自制的微压痕仪上，利用洛氏尖压头进行了6种不同载荷下的压痕试验，每种载荷下压入3次，取均值。典型的载荷—位移曲线如图3所示。

利用最小二乘法，对6种不同载荷下的系统总柔度C与1 Fm数据进行线性回归，其曲线如图4所示。计算得到的加载机构的柔度C1为9.594×10-6mm/N，即加载机构的刚度为1.04×105N/mm。

4 结论

利用压痕法测试材料的力学性能时，位移的精度受到加载机构的刚度影响。本文根据Oli⁃ver-Pharr模型，建立了系统的总柔度与最大压痕载荷的关系，通过实验，可以快速地测量加载机构的刚度，从而为获得高精度的压痕载荷—位移曲线提供帮助。

［1］周向阳，蒋庄德，王海容.仪器柔度对压入法测试结果的误差影响与校准［J］.计量学报，2007（04）：339-343.

［2］W.C.Oliver，G.M.Pharr.Measurement of hardness and elastic modulus by instrumented indentation：Advances in understanding and refinements to methodology［J］.J.Mater.Res，2004（19）：3-20.