含度量误差的毛竹相容性生物量模型

郭孝玉，孙玉军，刘 俊

(1.江西农业大学 林学院，江西 南昌 330045;2.北京林业大学 林学院，北京 100083;3.华东林业调查规划设计院，浙江 杭州 310019)

森林生物量作为森林生态系统最基础的数量特征，是评价森林生产力、森林碳储量等最重要的指标，它既能表明森林经营的状况和开发利用的潜力，又能反映森林与其环境间物质、能量间的复杂关系［1-2］。林木生物量模型是森林生物量监测与评估的基础，也是编制林业经营决策数表的依据。

生物量建模是一项基础研究，国内外已取得很多研究成果，涉及线性和非线性模型［3-14］。由于林木生物量涉及树干、树枝、树叶、树根等各个分量，但许多研究对生物量模型的兼容性缺乏考虑［6，15-17］，导致模型各分量估计值相加与总量估计值不相等。近年来许多学者对相容性生物量模型进行研究;唐守正等［1］设计了5种解决生物量相容性问题的方案，提出的最优方案是以树干生物量为控制量，采用2级代数和拟合分配联合估计法;Parresol［3］提出采用非线性似然无关回归方法来解决非线性生物量方程的可加性问题;曾伟生和唐守正［18］利用度量误差模型方法并考虑比值函数分级联合控制和比例函数总量直接控制2种方案构建了以地上总生物量为基础的相容性方程系统，表明分级联合控制方案和总量直接控制方案效果一致［19］，Zeng等［20］提出采用哑变量模型构建相容性生物量模型。联立方程组是解决相容性生物量模型最常见的方法，其最重要的因素是控制生物量分配比例函数，使各分量之和等于总量［21］，但目前采用的比例函数一般是以生物量方程为基础。报道中未见以生物量比值因子作为比例函数进行研究［22］。为此，本文以毛竹生物量数据为例，利用度量误差模型方法，比较2种不同构建相容性生物量模型系统方法，以期对生物量建模提供一些参考。

1 研究材料与方法

1.1研究数据

本文所用生物量数据为我国武夷山脉南麓(福建省三明市将乐县)山地毛竹的立木单株生物量实测数据。样本采集考虑本地区毛竹胸径及竹度，通过样地设置与调查，按2年为1竹度将竹龄划分为Ⅰ、Ⅱ、Ⅲ以上3个龄级，径级划分为4、6、8、10、12、14 cm及以上，共收集25株样木。实测样木胸径、冠幅，将样木伐倒后测量树高(竹杆长度)和冠长(树高减去活枝下高)。地上部分严格按1 m分层，分竹杆、枝、叶称总鲜质量，并分段分别采集各器官样品带回实验室;地下生物量由竹蔸及其2 m长竹鞭根系，分级称重并按比例采集样品带回实验室，在105℃恒温下烘干至恒质量，根据样品干物质率分别计算样木各器官干物质重量，并汇总得到地上、地下部分及单株总生物量。

表1 毛竹单株生物量实测数据的基本信息Tab.1 The basic information of the single-tree biomass data for modeling

1.2 研究方法

当自变量和因变量的观测值中都含有度量误差时，通常的回归模型估计方法就不再适用，而必需采用度量误差模型方法［18，22］。非线性度量误差联立方程组估计方法可解决林木各器官 (杆、枝、叶、根和总量)生物量不相容的问题，非线性度量误差模型的一般形式如下:

f为m维向量函数，yi是p维误差变量 (error-in-variable)的观测数据，yi是Yi的未知真值，Yi是1×p维向量真值yi的观测值，ei为Fi与yi间的误差值;xi为1×q维向量无误差变量(error-out-variable)的观测值;误差的协方差矩阵记为Φ =，ψ是ei的误差结构矩阵，σ2为估计误差，该方程组被称为非线性度量误差联立方程组。c是k×1维参数向量;一般满足p＞m;当f是(xi，yi)和c的双线性函数时，就是线性度量误差模型，否则称为非线性度量误差模型。

1.2.1 独立生物量模型 (1)生物量方程。通过3种独立生物量模型(线形方程(y=ax1+bx2+c)、异速生长方程(y=ax1bx2c)和改进型异速生长方程(y=axbexp(cx2))的比较研究。模型中备选自变量为胸径(D)、树高(H)、冠幅(CW)、活枝下高(h)冠长(CL)和竹度(A)及其内生二元变量DH、D2H、DA、CW2CL。按照模型中自变量个数分为一元和二元生物量模型，拟合过程先确定方程的最佳自变量(x1)，再确定拟合方程的次优自变量(x2)，模型拟合采用Spss19.0统计软件中的非线性回归程序(NLR)，采用最小二乘法收敛模型参数。模型评价采用决定系数(R2)、平均相对绝对残差(MRAE)、均方误差(SEE)、模型参数变动系数(CV)等4个指标［11，23］筛选独立基础模型的自变量，确定总量及分量的最佳模型。

3种独立生物量模型比较研究表明，不同模型结构的二元生物量模型精度均高于一元最优生物量模型，其中均以改进型异速生长方程的模拟精度最优。因此，毛竹总量及各分量的独立生物量方程的模型结构形式见(2)，令 f(i)=f(x)，(i=1、2、3、4、5、6 和 7 分别代表单株总生物量、地上、地下、竹杆、树冠、枝和叶生物量)。

式(2)中由异速生长模型和指数模型构成，x1、x2为模型中自变量，a、b和c为模型参数。

(2)生物量比值模型。生物量比值因子(BRF)为单株组分生物量与其竹杆生物量的比值，各组分生物量比值因子可能为一常数值，生物量比值模型基于改进异速生长方程拟合(3)，令g(i)=g(x)，(i=1、2、3、4、5、6 和7 分别代表单株总生物量、地上、地下、竹杆、树冠、枝和叶生物量)。

式(3)中，x1、x2为模型自变量，a、b、c为模型参数。模型自变量筛选、模型拟合及模型平均均与生物量方程拟合一致。

1.2.2 相容性生物量模型系统 (1)以生物量方程为基础总量分级控制法。本文中总量分级控制相容性联合估计方法参照曾伟生和唐守正(2010)提出的研究思路，以总生物量为基础，采用3级控制的方法对生物量进行相容性模型的建立，1级控制变量为单株总生物量，将毛竹单株总生物量的独立模型进行回归估计，通过一级控制按比例分配使地上部分生物量和地下生物量之和等于总生物量;2级控制变量为地上部分生物量，通过二级控制按比例分配使地上部分生物量等于竹杆生物量和树冠生物量之和;3级控制变量为树冠生物量，使树冠生物量等于树枝生物量和树叶生物量之和，具体方案如下:

1级控制:

式中 f2(x)、f3(x)、f4(x)、f5(x)、f6(x)、f7(x)分别为各毛竹地上部分、地下部分(竹蔸 +竹鞭)、竹杆、树冠、枝、叶生物量的最优独立模型;为总生物量的估计值，为最优总生物量独立模型，为联合估计后的估计值。

以总生物量为基础，运用非线性度量误差联立方程组的联合估计方法进行逐级联合估计，具体步骤如下:

1级控制:首先对单株总生物量进行独立模型回归，得到总生物量模型参数和估计值，将f2(x)和f3(x)的独立模型代入式(4)和(5)简化为如下联立方程组:

(2)以生物量比值模型为基础的总量直接控制法。以总量为控制，直接按生物量比值的比例关系将竹杆、枝、叶、根联立方程组，竹杆生物量比值因子为1，模型结构形式如下:

将生物量比值因子BRF3、BRF4、BRF6、BRF7的独立模型(表3)代入式(17)中，并对公式进行简化得到如下联立方程组为:

式(18)中，为了简化方程，令a3/a6=k1、b3/b6=k2，则式中D和A为不含度量误差变量，和为含度量误差变量，a6、b6、a3、b3、c3为联立方程的待估参数，其初始值一般为独立模型参数。

1.2.3 模型模拟及评价 采用Forstat2.1软件对上述非线性度量误差联立方程组的参数进行估计。模型参数估计方法选择牛顿-唐算法、单纯形法，误差变量的估计方法采用“唐_法”(TSEM)。模拟目标指定的允许误差=0.000 001。模型评价采用决定系数(R2)、均方误差(MSE)、平均误差(ME)、平均相对误差绝对值(MRAE)4个指标［24］评价模型的预测能力。为检验所拟合的生物量模型是否存在系统偏差，对其进行精度验证。设y为实际观察值，yi为模型预估值，建立直线方程y=a+byi，采用F检验检查a是否近似为0，b是否近似1。

2 结果与分析

2.1 独立生物量模型

2.1.1 生物量方程 毛竹最佳生物量方程拟合结果见表2，由表可知，改进异速生长方程拟型的拟合效果好，模型的决定系数达0.83以上，竹杆生物量和地上总生物量模型最佳R2达0.92;毛竹生物量的最佳预测变量是胸径，其次是竹度或冠长因子，竹度对竹杆生物量、地上总生物量、地下根系生物量和单株总生物量影响较大，而冠长对树冠生物量模型(包括枝、叶)影响较大;树冠生物量模型预测精度相对较低，这可能也与树冠容易受多种外界环境的影响有关，如林木之间的竞争导致树冠偏冠、人为或大风摇晃导致毛竹断了梢头、病虫害等导致树叶受损。

2.1.2 生物量比值方程 毛竹最佳生物量比值模型拟合结果见表3。研究发现毛竹叶生物量比值因子很稳定，其平均值为0.089 9，其它生物量比值方程随着胸径、活枝下高或竹度的变化而呈显著变化(p＜0.001)，R2达0.30～0.49，地下根生物量、单株生物量、树冠生物量和枝生物量最佳估测BEF的预测因子为胸径，其次是活枝下高或竹度，地下生物量比值因子随胸径、年龄的影响较大，毛竹是禾本科植物，第一年出笋发竹后竹杆的形态结构基本不变，而生产力更多分配于地下根系生物量，而且随年龄增加毛竹根系生物量也增加。

表2 毛竹各组分生物量方程Tab.2 The biomass equations of components for Moso bamboo

表3 毛竹生物量比值模型Tab.3 The biomass ratio factor equations of components for Moso bamboo

2.2 以总量为基础相容性模型

2.2.1 总量以生物量方程为基础的分级控制模型系统 总量以生物量方程为基础的分级控制方程系统结果见表4∶1级控制:地上与地下相容性生物量模型。以整株总生物量为基础，通过1级控制，模拟结果见表4。模型拟合的决定系数高，均达到0.96以上，地上、地下生物量联立估测模型的平均残差ME分别为0.011 1和－0.006 1。2级控制:`相容性竹杆与树冠生物量模型结果表明，模型拟合的决定系数较高，均达到0.94及以上，竹杆和树冠生物量联立估测模型的平均残差ME分别为－0.108 4和－0.069 9，平均决定残差分别为1.454 kg和0.551 kg。3级控制:枝与叶相容性生物量模型结果。以树冠生物量为基础，通过3级控制，按联立枝、叶生物量方程组拟合的决定系数高，均达到0.93以上，枝、叶生物量联立估测模型的平均残差ME分别为－0.018 5和－0.029 7。

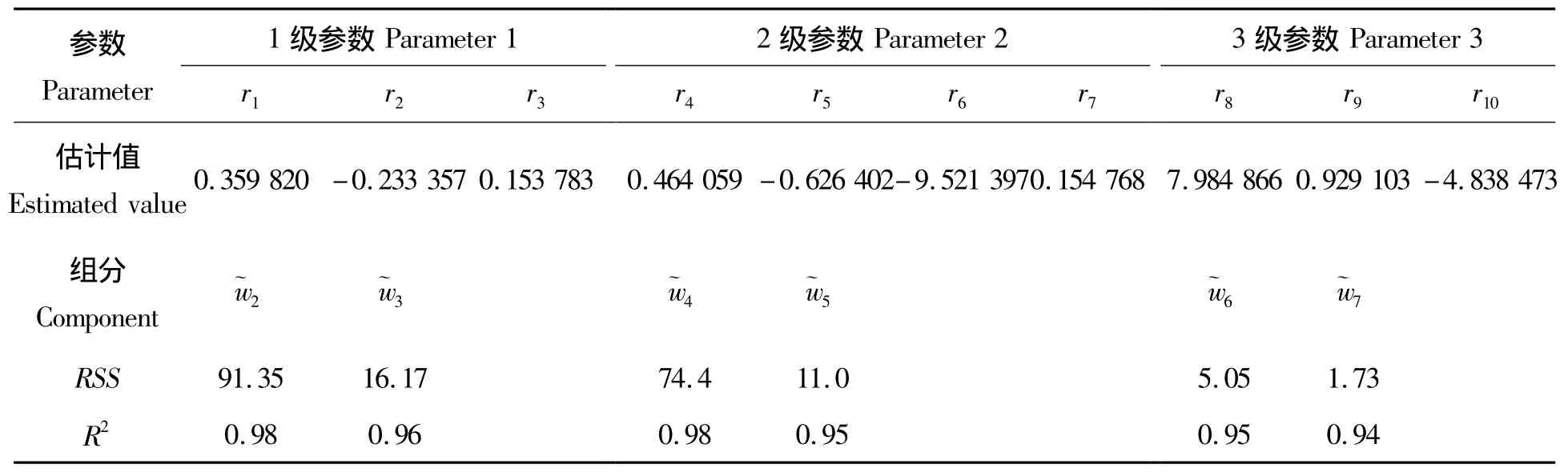
表4 分级控制法相容性生物量模型系统拟合结果Tab.4 The compatible biomass model by hierarchical control method based on independence biomass equations

2.2.2 总量以生物量比值模型为基础的直接控制模型系统 以单株总生物量估测模型为基础，采用生物量比值因子直接控制联立方程组法，参数联合估计结果见表5。各分项联合估计的决定系数R2在0.88～0.97，拟合效果均较好，竹杆生物量拟合效果最佳，其平均误差为0.071，平均相对绝对误差为21.8%。竹杆生物量是毛竹单株生物量的主要组成部分，约占毛竹生物量的62%，而叶生物量分配最少。随着生物量分配比例的减少，其平均相对绝对误差在增大。

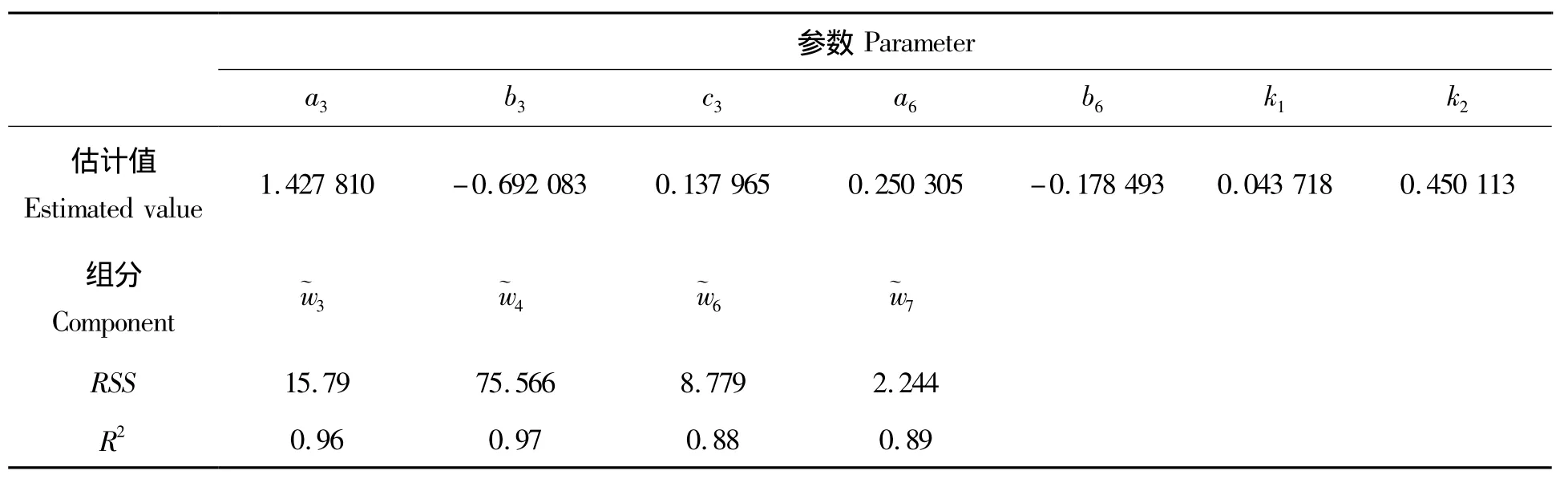
表5 直接控制法相容性生物量模型系统拟合结果Tab.5 The compatible biomass model by controlling directly method

2.3 模型比较

2.3.1 模型评价 利用总量以生物量方程为基础的分级控制模型系统［方程(10)—方程(16)］和总量以生物量比值因子方程为基础的直接控制模型系统［方程组(17)—方程(18)］对建模数据进行预测，得到模型评价指标见表6。

表6 总量分级控制法和直接控制法的评价指标比较Tab.6 The comparisons of compatible biomass equations between hierarchical control method and directly control

2种方法预测精度都较高，总体而言，直接控制法拟合的平均预测误差要优于分级控制法。分级控制法的根系、竹杆、枝、叶生物量预测结果均呈低估，直接控制法的枝、叶也呈低估现象;分级控制的地上总生物量估测结果呈高估，而直接控制法的地上、竹杆和根系生物量呈高估，相比而言，直接控制法比分级控制法的预测误差较小。从平均相对绝对误差(MRAE)比较，除了树冠生物量和枝生物量，直接控制法的RMAE均小于分级控制法。随着分级数增加，传递误差也增加，如总量分级控制法从1级控制平均绝对误差25.5%到2级的26.1%、3级的37.0%，特别是叶的平均相对误差达43%左右，这可能与叶占总生物量的比例较小，而且易受外界环境的影响而产生较大变动，如病虫害、大风、雨雪冰冻灾害等;综合而言，直接控制法优于分级控制法。竹杆生物量估测效果优于树冠生物量模型估测，竹杆生物量具有较高稳定性，主要受竹子胸径、树高大小以及竹子密度影响，而树冠受影响的因素较多，如林分密度、立地条件、树冠长度等。

2.3.2 模型检验 模型检验采用线性检验，分析模型估计值与实测值之间的线性关系，分析检验结果见图1和表7。线性回归参数检验表明:秆、枝、叶和根的一元线性模型的斜率参数b值均达显著水平，并在0.95～1.05，近似等于1;模型截距项a值未达显著性。从图1可知，2种相容性生物量模拟方法比较显示，不同组分生物量值的模型估计值与实测值的回归关系均在对角线附近，回归系数也接近等于1。从拟合精度R2来看，以生物量比值因子方程为比例函数的相容性上生物量的模型系统中，杆和根系生物量拟合精度较高。枝和叶生物量回归检验模型决定系数R2达0.84和0.85～0.94，枝生物量估测效果优于叶生物量模型估测。

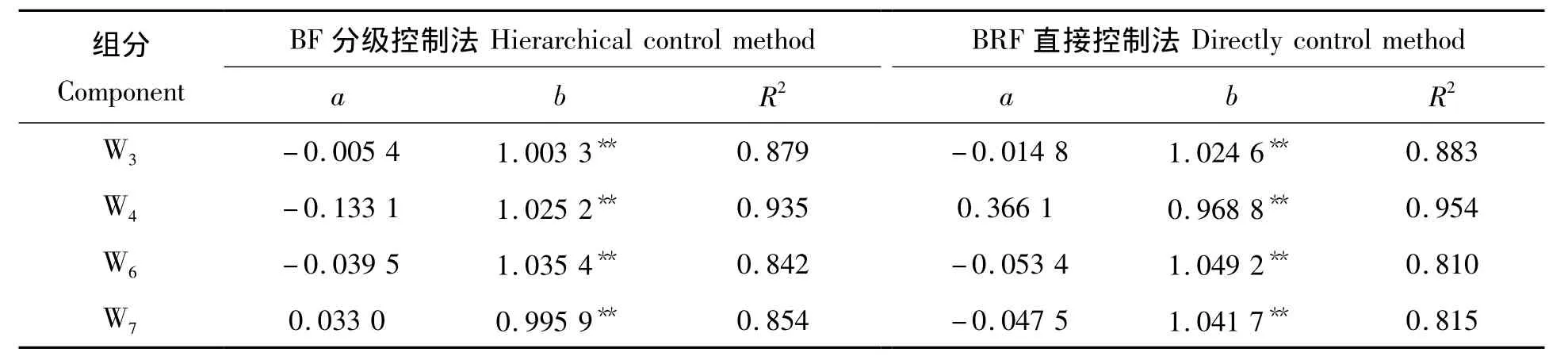
表7 相容性模型估计值与实测值回归模型参数检验Tab.7 The F test for parameters of linear regression of compatibility model against measured values

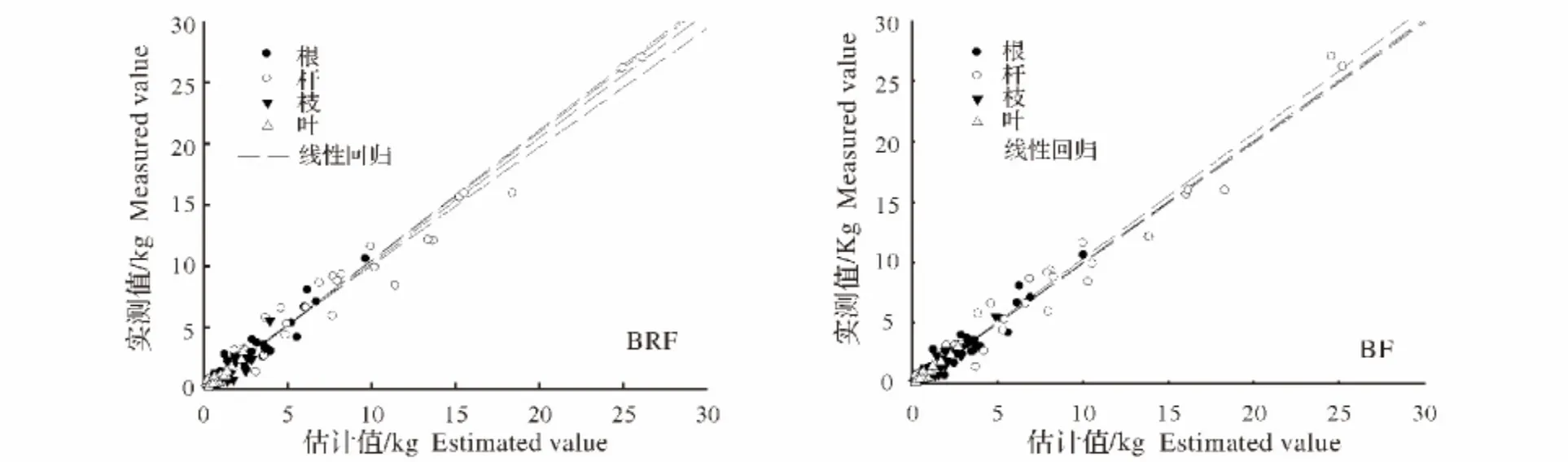
图1 2种相容性生物量模型估计值与实测值回归关系(BRF为直接控制法、BF为分级控制法)Fig.1 The relationship of the compatibility biomass estimate values with the measured values(BRF for direct control and BF for hierarchical control，respectively)

3 结论与讨论

本文以毛竹生物量为例，利用度量误差模型方法，建立了毛竹总生物量与地上部分、地下根系部分、竹杆、树冠、树枝、树叶生物量以及各分项生物量间的相容性模型。通过方程组联合估计方法能解决各分项生物量相容性问题，拟合精度及预测精度均较高，R2达0.84～0.94，但模型系统误差随着分级级数的增加，传递误差也增大。文章对2种方案进行详细比较分析表明2种方法拟合效果比较接近，总体而言直接控制法优于分级控制法，这与曾伟生和唐守正(2010)［18］、符利勇等(2014)［19］研究结果较一致。直接控制法优于分级控制法的可能原因:依据误差传播定律［25］，模型在拟合过程中级数越多导致误差累计越大，分级越低级的生物量模型估测值就越不稳定。

本文以生物量比值方程作为基础模型的直接控制法，通过方程组联合估计相容性生物量模型系统参数，可采用代数加和法，通过模拟得到的竹杆、枝、叶相容性生物量方程，地下根系等于总量减去杆、枝、叶生物估计值。通过研究区样地调查数据的实证分析，发现总量以生物量比值方程为基础的直接控制法更符合生物量分配规律，而总量以生物量方程为基础的分级控制法可能导致部分样地枝、叶生物量被严重低估现象。解决总量与分项相容性的方法有比例平差法、方程组联合估计法，有研究表明2种方法的比较差异不是特别明显，联合估计法略优于比例平差法［19］，比例平差法是最简单直接的方法，在实践中不要求高精度时，可以直接采用。所谓相容性就是指生物量中各分项(杆、枝、叶和根)之和等于总生物量，或(杆、枝、叶)之和等于地上总生物量，本质上就是满足各分项占总量的比例之和等于1。代数和法也是解决相容性的一种方法，唐守正等［1］比较研究了5种解决相容性的方案后认为直接控制各分项之和等于总量的方法最佳;付尧等［24］采用3级代数和拟合分配长白落叶松生物量相容性模型，也得到较好的拟合效果。

综合比较，最佳的毛竹相容性生物量估测模型如下:

生物量模型应用有尺度性或地区域等问题，不同地域生长的毛竹在干形、生物量分配等往往有差异，即在小尺度或小流域上所建立的生物量模型外推到大尺度或大区域时，需要采集样本进行模型验证、调整参数。

［1］唐守正，张会儒，胥 辉.相容性生物量模型的建立及其估计方法研究［J］.林业科学，2000，36:19-27.

［2］董利虎，李凤日，贾炜玮，等.含度量误差的黑龙江省主要树种生物量相容性模型［J］.应用生态学报，2011，22(10):2653-2661.

［3］Parresol B R.Additivity of nonlinear biomass equations［J］.Can J For Res，2001，31(5):865-878.

［4］Bi H，Turner J，Lambert M J.Additive biomass equations for native eucalypt forest trees of temperate Australia［J］.Trees，2004，18(4):467-479.

［5］Zhang Y J，Borders B E.Using a system mixed-effects modeling method to estimate tree compartment biomass for intensively managed loblolly pines—an allometric approach［J］.For Ecol Manage，2004，194(1/3):145 －157.

［6］Chave J，Andalo C，Brown S，et al.Tree allometry and improved estimation of carbon stocks and balance in tropical forests［J］.Oecologia，2005，145(1):87-99.

［7］Fehrmann L，Lehtonen A，Kleinn C，et al.Comparison of linear and mixed-effect regression models and a k-nearest neighbor approach for estimation of single-tree biomass［J］.Can J For Res，2008，38:1-9.

［8］Zeng W，Tang S.Modeling compatible single-tree aboveground biomass equations for masson pine(Pinus massoniana)in southern China［J］.Journal of Forestry Research，2012，23(4):593-598.

［9］罗云建，张小全，王效科，等.森林生物量的估算方法及其研究进展［J］.林业科学，2009，45(8):2009，08:129-134.

［10］刘琪璟.嵌套式回归建立树木生物量模型［J］.植物生态学报，2009，33(2):331-337.

［11］郭孝玉，孙玉军，刘凤娇.不同估算树冠生物量方法的比较——以长白落叶松林为例［J］.林业资源管理，2010(5):41-47.

［12］符利勇，曾伟生，唐守正.利用混合模型分析地域对国内马尾松生物量的影响［J］.生态学报，2011，31(19):5797-5808.

［13］曾伟生，唐守正.立木生物量方程的优度评价和精度分析［J］.林业科学，2012，47(11):106-113.35(2):17-21.

［14］王轶夫，孙玉军，郭孝玉.基于BP神经网络的马尾松立木生物量模型研究［J］.北京林业大学学报，2013，35(2):17-21.

［15］郑容妹，郑郁善，丁闽锋，等.苦竹生物量模型的研究［J］.福建林学院学报，2003，23(1):61-64.

［16］Peichl M，Arain M A.Allometry and partitioning of above-and belowground tree biomass in an age-sequence of white pine forests［J］.For Ecol Manage，2007，253(1/3):68-80.

［17］Ketterings Q M，Coe R，van Noordwijk M，et al..Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests［J］.For Ecol Manage，2001，146(1):199-209.

［18］曾伟生，唐守正.利用度量误差模型方法建立相容性立木生物量方程系统［J］.林业科学研究，2010，23(6):797-802.

［19］符利勇，雷渊才，曾伟生.几种相容性生物量模型及估计方法的比较［J］.林业科学，2014，50(6):42-54.

［20］Zeng W S，Zhang H R，Tang S Z.Using the dummy variable model approach to construct compatible single-tree biomass equations at different scales—a case study for Masson pine(Pinus massoniana)in southern China［J］.Canadian Journal of Forest Research，2011，41(7):1547-1554.

［21］Dong L，Zhang L，Li F.A compatible system of biomass equations for three conifer species in Northeast，China［J］.Forest E-cology and Management，2014，329:306-317.

［22］唐守正，李勇.一种多元非线性度量误差模型的参数估计及算法［J］.生物数学学报，1996，11(1):23-27.

［23］李凤日.长白落叶松人工林树冠形状的模拟［J］.林业科学，2004，40(5):16-24

［24］付尧，马炜，王新杰.小兴安岭长白落叶松相容性生物量模型的构建［J］.东北林业大学学报，2011，39(7):42-45.

［25］冯仲科，刘永霞.森林生物量测定精度分析［J］.北京林业大学学报，2005，27(S2):108-111.