基于Monte Carlo-SHALSTAB模型的滑坡危险性评价——以福建省德化县为例*

陈悦丽，陈德辉，李泽椿，黄俊宝

（1.南京信息工程大学大气科学学院，江苏南京210044；2.中国气象局数值预报中心，北京100081；3.国家气象中心，北京100081；4.福建省地质环境监测中心，福建福州，350002）

基于Monte Carlo-SHALSTAB模型的滑坡危险性评价
——以福建省德化县为例*

陈悦丽1，2，陈德辉2，李泽椿1，3，黄俊宝4

（1.南京信息工程大学大气科学学院，江苏南京210044；2.中国气象局数值预报中心，北京100081；3.国家气象中心，北京100081；4.福建省地质环境监测中心，福建福州，350002）

滑坡灾害是福建省德化县最常见的地质灾害之一，特别是在雨季。研究表明岩土参数的空间分布非均匀性是滑坡危险性评价不确定性的主要来源，因此将岩土参数，特别是凝聚力和内摩擦角，看作随机变量。考虑岩土参数的空间变化以及非均匀性，提出了一种用来进行滑坡危险性评价的可能性模型。模型首先利用Monte Carlo方法随机生成参数值，然后应用SHALSTAB（SHAllow Landslide STABilitymodel）模型计算安全系数，最后统计研究单元的失稳概率。以福建省德化县的滑坡危险性为例，通过历史滑坡资料与滑坡危险区评价结果进行比较，有90%以上的历史滑坡点位于危险区域内。其中31.70%的滑坡点落在低危险区，9.83%的滑坡点落在危险区，30.96%的滑坡点落在较高危险区，17.94%的滑坡点落在高危险区内。说明该模型在滑坡危险性评价中具有较好的应用前景。

滑坡；滑坡危险性评价；Montecarlo；SHALSTAB模型

滑坡危险性是回答在某一时间段内（时间）一个地方（空间）遭受滑坡危害的概率［1］。滑坡危险性评价方法通常依据研究区域的大小及相关资料的详细程度来选择。如果研究区域较小，而且可以获得岩土工程的详细资料，可以用滑坡物理模型，也就是稳定性的各种计算模型来评价斜坡的稳定性。如果区域较大，且过去的滑坡研究较为充分，可以用统计模型开展滑坡的危险性评价研究。总体而言，滑坡危险性评价的方法可以分为统计模型和物理模型。

目前，国内外开展的滑坡危险性评价主要是基于GIS的统计模型。Ercanoglu等基于GIS采用模糊数学方法，选取了坡角、坡型、风化程度、水文条件以及地形等因子共同建立滑坡敏感性评价图［2］。Baeza等应用多元统计方法计算，确定选取的不同因子的贡献率，最后筛选得出最具有评价效用的几个因子，进行滑坡危险度区划［3］。殷坤龙等利用GIS制图的基本原理，在陕西省秦巴山区的汉江河进行了灾害危险性评价［4］。王磊等在甘肃省甘谷县开展了地质灾害危险性评价，选择历史地质灾害发育程度、地形地貌、工程地质岩组、地质构造、水文条件、植被条件、降雨量、人类工程活动等影响因素，建立了相应的地质灾害危险性评价指标体系［5］。范强等应用ArcGIS平台，利用证据权法对贵州桐梓河流域进行了滑坡易发性分区［6］。

基于GIS的统计模型大多是建立在影响因子的选择及其权重确定的基础上的，选择不同的影响因子和权重方法，评价的结果存在差异。

物理模型是以滑坡发生的物理力学为基础，需要边坡较为详细的岩土力学参数，结果会受到数据量和数据精度的影响。李秀珍等对降雨入渗诱发斜坡失稳的物理模型适用性进行了详尽的分析［7］。相对于统计模型，物理模型可以较为客观地反映边坡的物理变化，其缺点是受到人力、物力等方面的考虑，缺乏较为详细的岩土力学参数，该方法通常只能适用于单个滑坡或者小范围区域。例如王旭春等在边坡尺度上实现基于力学原理的滑坡稳定性计算［8］；陈伟等利用《滑坡防治工程设计与施工技术规范》推荐的稳定性计算公式计算单体滑坡灾害危险性评价［9］。近几年，滑坡危险性评价的物理模型已经由单一的边坡稳定性模型，逐渐发展为耦合模型，将水文模型与稳定性模型进行耦合，其中SHALSTAB模型是目前被广泛认可的降雨型滑坡预测工具之一［10］。

国内有很多学者使用SHALSTAB模型进行区域降雨诱发的滑坡预测。例如康超等利用SHALSTAB模型选择黄土高原甘肃陇东地区华池县作为研究区，选取了70多个采样点通过现场勘探和试验得到岩土参数，计算结果显示总体正确率为70.23%［11］。王佳佳等利用已有的岩土参数，基于SHALSTAB模型，对三峡库区巴东新城进行了滑坡灾害预测［12］。通常需要在野外打钻取样，通过实验分析获取水土参数值。如果研究区域面积较大，考虑人力、物力和时间等的成本，并且试验测试本身存在误差，不可能获取大范围准确的水土参数［13］。特别是坡体的性质，例如内摩擦角和凝聚力，具有内在的空间非均匀性［14-15］。前人在利用SHALSTAB模型进行滑坡预测时，没有考虑水土参数的不确定性对滑坡预测结果的影响，我们称之为“定值-SHALSTAB”模型。

岩土参数具有空间分布的非均匀性，而在计算边坡的稳定性时，凝聚力和内摩擦角参数是模型不确定性的主要来源［16-17］，因此很多学者针对土体凝聚力和内摩擦角的性质开展了大量的研究工作［18］。罗冲等通过对三峡库区万州区的滑坡综合分析，对滑带土进行了统计分析，认为凝聚力服从对数正态分布，内摩擦角服从正态分布［19］。Chowdhuny的研究表明凝聚力和内摩擦角呈正态分布［20］。有的研究者利用水土参数的分布特征，将内摩擦角和凝聚力参数看作一个随机变量，而不是单一的一个值［21-23］。在进行滑坡地质灾害预测，能获取的采样样本数有限，利用岩土参数的分布特征，为解决岩土参数空间分辨率不足的问题提供了可能的解决方法。

基于上述的思路，将获取精确水土参数的需求，转化为获取水土参数的概率密度分布曲线，从而解决难于获取水土参数的问题［24-25］。蒙特卡罗模拟法（Monte-Carlo、模拟法，或MCSM）是已知通过随机变量的概率分布函数，随机模拟和统计试验求可靠度的数值模拟方法，其理论依据是大数定律，基本思想是借助计算机手段产生足够多的模拟次数，以逼近真实状态。利用MCSM方法对凝聚力和内摩擦角参数进行多次随机抽样，将抽样结果输入SHALSTAB模型，计算滑坡可能的失稳概率，从而实现区域滑坡危险性的概率评价，我们将称之为“Monte Carlo-SHALSTAB”模型。

定值-SHALSTAB模型是将所有岩土参数看作一个单一的值。虽然岩土参数的值是客观确定的，但是由于测量设备、试验设备以及场地条件的限制，各指标难以精确测定，且在边坡的不同空间内各指标值是变异的。在考虑岩土参数的空间分布不均的基础上，判断滑坡的稳定性更加科学合理［26］。本文主要是利用Monte Carlo-SHALSTAB模型，在充分考虑输入参数不确定性基础上，对福建省德化县进行滑坡危险性的概率评价。

1 研究区域

德化县位于福建省中部，隶属泉州市管辖，东西长62.1 km，南北长60.4 km，总面积2 232.6 km2，总人口302 503人。德化县属亚热带山地气候，根据德化县气象局1990-2005年降雨量资料，全县年降雨量在1 301.5～2 343.6 mm之间，多年平均降雨量1 855.9 mm。3-6月为雨季，占全年降水的42.9%；7-9月为台风雷阵雨季，占全年降水的41.8%，表现为台风暴雨或大暴雨，雨量大而集中，是地质灾害的易发期：10月至翌年2月为少雨季［18］。由于海拔悬殊，地形复杂，降雨空间分布地域差异较大，以戴云山为界，具有从南部向北部递减的趋势。

德化县的岩土体以坚硬块状火山岩岩组为主，占全区面积的65.2%，其次还分布有坚硬块状侵入岩岩组、坚硬—较坚硬块状变质岩岩组和坚硬块状碳酸岩岩组等。土体多为砂质粘土，为德化县地质灾害的主要致灾体。据调查德化县内地质灾害主要类型有滑坡、崩塌和地面塌陷等，其中滑坡为545处，占地质灾害总数量的92.06%。滑坡类型主要为浅层小型滑坡为主，滑坡体厚度一般小于6 m，其中98.17%的滑坡属于自然滑坡。地质灾害的发生与月降雨量关系密切，每年5-8月为滑坡的高发时段，属于典型的气象—地质灾害耦合性［18］。

德化县地以低中山、中低山为主，其中低中山占全县面积的39.4%，中低山占44.8%，丘陵占12.6%，河谷盆地及河谷阶地占3.2%，零星散布于群山之中。境内坡度较大，有较大区域的坡度大于35°，易于发生滑坡灾害（图1）。根据福建省地质环境监测院的野外探测，其土壤深度分布为1.6～9.2 m，德化县北部、西部以及东南部区域，土壤厚度较大（图2）。

2 Monte Carlo-SHALSTAB模型原理

Montgomery和Dietrich于1994年开发了一种以等高线和栅格单元为基础的滑坡稳定性预测模型SHALSTAB模型。SHALSTAB模型是基于无限边坡的滑坡稳定性模型，以广义摩尔-库伦破坏准则为基本原理，安全系数（the factor of safety，FS）可以根据式（1）计算［27-28］：

式中：c为土壤凝聚力（N／m2）；γ为土壤容重（N／m）；γω为水容重（N／m）；z为地下水位高度（距离地表的高度，m）；hω为饱和土壤厚度（距离滑动面的高度，m）；α为边坡的坡度（°）；φ为摩擦角（°）。为了使得模型简化，式（1）假设地下水位高度与边坡表面、滑动面平行，并且位于高度hω。结合TOPMODEL水文模型，式（3）～（1）可转变为：

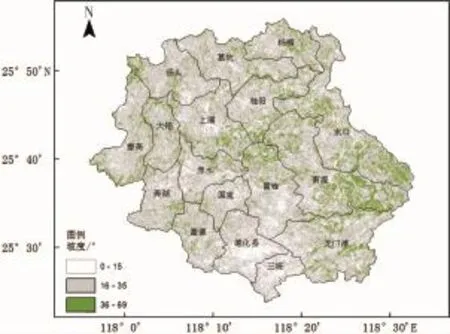
图1 德化县坡度

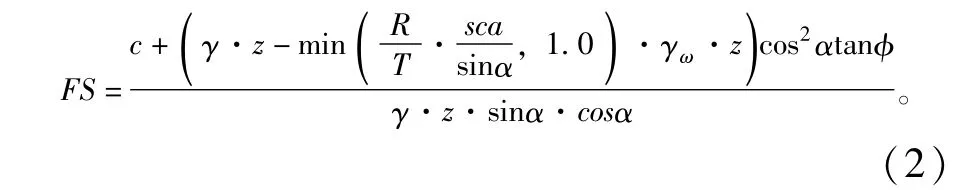
式中：R为降雨强度；T为土壤传导率，即土壤渗透系数与土壤厚度的乘积；sca为单位集水面积。被称为土壤湿度指数，当湿度项大于1时，认为土壤已经饱和，产生了饱和流。当FS小于1时，边坡有发生滑坡的可能，当FS大于1时，边坡处于安全状态。

由于受到工作时间和经费等的限制，研究区域内的取样样本数量有限。并且岩土力学参数本身具有很强的空间不一致性，也难以获得精确的土壤力学参数的空间分布。如果仅仅赋予土壤力学参数一个值，可能导致预测的结果与实际情况有较大的差异。考虑土壤力学参数的不确定性问题，在评价滑坡的稳定性上具有重要的意义。凝聚力和摩擦角是模型不确定性的主要来源，凝聚力和摩擦角通常呈正态分布，因此可以将土壤凝聚力和内摩擦角看作随机变量，服从正态分布，而不是确定的单一的值。

蒙特卡洛方法（Monte Carlo）是以概率统计理论为基础，实现从已知概率分布抽样，建立随机变量的估计值，构造符合一定规则的随机数。基于野外采样和室内试验的结果，可以获得土壤力学参数的统计特征。由于Monte Carlo方法简单易用，本研究根据土壤力学参数的统计特征，利用Monte Carlo方法随机生成土壤的力学参数，利用SHALSTAB模型进行计算，每个格点都可以获得一系列的安全系数，从而计算该格点发生滑坡的概率。

式中：P为滑坡发生的概率；n为随机抽样的次数；n′为随机试验中FS小于1的次数。

利用岩土参数的分布特征，通过Monte-carlo方法模拟参数的随机分布，建立在概率论基础上的可靠度被引入到边坡的稳定性评价中，使得滑坡的危险性评价方法由确定性评价改进为概率评价，评价结果更为科学和精确。

3 结果分析与讨论

3.1 模型参数

根据福建省地质环境监测院在德化县进行的野外调查和室内试验的数据，对样本的凝聚力和内摩擦角数据进行正态分布的拟合度测试，均通过了显著性水平为0.05的正态分布检验。根据采样实验数据，利用Matlab软件进行正态分布拟合：凝聚力的平均值为12.21 kPa，方差为6.15；内摩擦角的平均值为21.06°，方差为6.18（图3）。这样的结果，与前面的学者的研究结论相符合，说明土壤的力学参数在很多区域大致符合正态分布特征。

由于德化县的坡积土主要为砂质粘土，其导水率较低，因此只要降雨强度达到20 mm／d，德化县境内的地形湿度指数基本都可以达到1，即地下水处于饱和状态。根据对德化县多年的日降雨量进行统计分析，有雨日的降水量达到20 mm以上是一个常态，并且当地形湿度指数为1时，边坡处于最危险的状态，因此在本研究中地形湿度指数项取1。这样的结果同时也说明，只要德化县的日降水达到中雨量级，滑坡的危险性概率就会变大。因此在开展防灾减灾工作时，不仅要防范大雨和暴雨可能诱发的滑坡灾害，也要重点防御中雨诱发的滑坡灾害。

3.2 滑坡危险性评价及其结果验证

基于Monte Carlo的滑坡-水文耦合模型，根据凝聚力平均值为12.21 kPa，方差为6.15，内摩擦角的平均值为21.06°，方差为6.18的正态分布特征，随机生成1000组土壤凝聚力和内摩擦角的值，从而每个格点都可以计算获得1000个FS的计算结果，统计每个格点FS＜1的概率，即该格点可能出现滑坡灾害的概率，结果显示在图4。德化县的西部以及中北部区域，都出现了大片滑坡危险性高概率的区域。德化县的南部区域由于地势平坦，坡度较小，滑坡危险性概率较低。

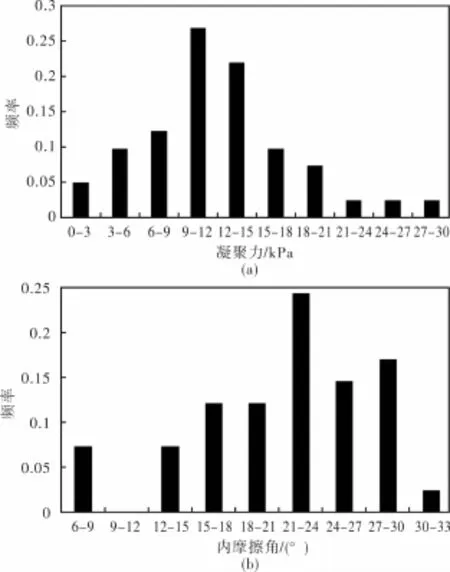
图3 土壤样品的土壤凝聚力（a）和内摩擦角（b）分布

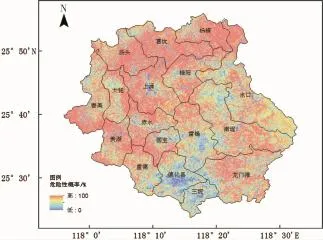
图4 德化县滑坡危险性概率图

KoKo等认为应选用边坡失稳概率20%作为阈值，当安全系数小于1的概率大于20%，就认为该格点属于危险区域［29］，Chowdhury等建议阈值取15%［16］，也有研究中阈值取10%［30］。根据表1的统计结果：阈值为10%时，90.42%的历史滑坡点在危险区域内；阈值为20%时，83.54%的滑坡点在危险区域内。为了使得更多的滑坡点在危险区域内，本文中滑坡危险性阈值取10%，即认为当边坡失稳概率大于10%时，该格点属于危险区域，若该格点的边坡失稳概率小于20%，该格点属于安全区域。将德化县滑坡灾害的危险区域，根据边坡失稳概率的不同，又分为四个级别。当该格点的失稳概率大于10%，小于60%时，处于低危险区；当失稳概率大于60%，小于80%，为危险区；当失稳概率大于80%，小于99%，则该格点处于较高危险区；如果该格点的滑坡发生概率大于99%，则该格点为高危险区。

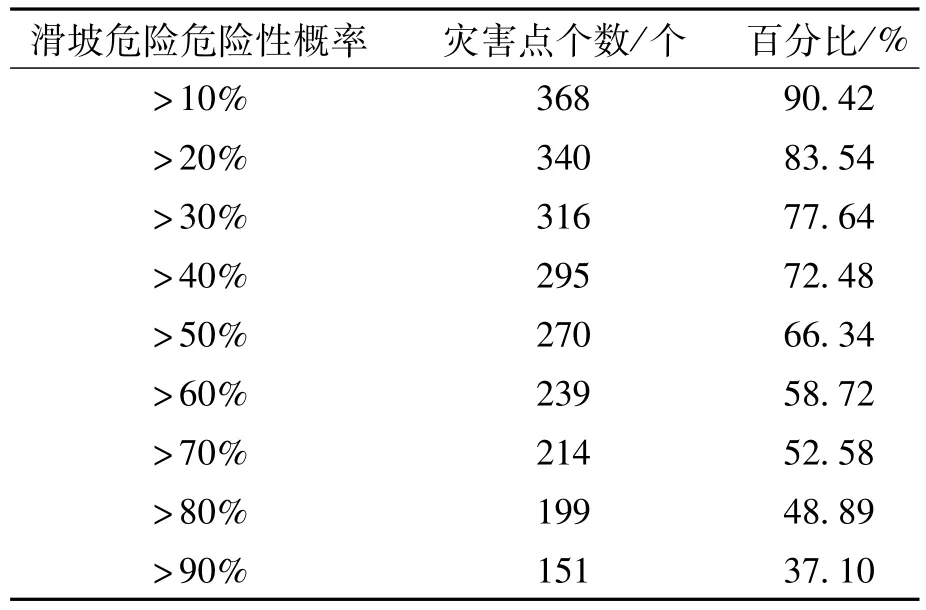
表1 研究区滑坡分布结果

“路无三尺宽，地无三分平”恰当地描述了德化县山高坡陡的地形特征，因此德化县也是滑坡灾害多发频发之地，是地质灾害多、危险等级高的地灾县。德化县滑坡灾害具有“点多、面广、危害大”的特点。图5中显示德化县北部、西部和东南部，都有大片的滑坡高危险区，其中的黑点代表407个历史降雨诱发型滑坡灾害点。图5所示的德化县滑坡危险性评价结果与《区域降雨型地质灾害气象预警技术研究》（“十一五”国家科技支撑计划重点项目课题成果之一）的评价结果接近［31］。《区域降雨型地质灾害气象预警技术研究》中采用不确定系数计算模型进行因子分析，选用Logistic回归模型对德化县的滑坡灾害进行了预警区划分。与之相较而言，Monte Carlo-SHALSTAB模型的评价结果精确到了每个格点，并且不需要历史滑坡资料作为先验知识，能更为便捷的开展滑坡危险性评价。

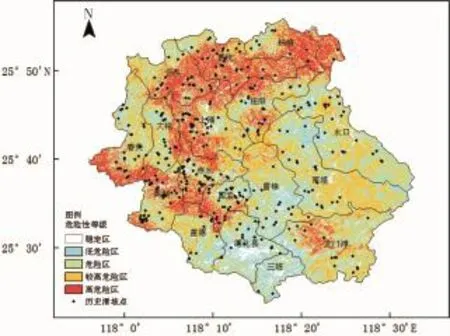
图5 德化县滑坡危险性等级图

根据记录的历史滑坡资料，对Monte Carlo-SHALSTAB模型的滑坡危险性评价效果进行进一步的检验。有90%以上的滑坡灾害点落在危险区域内，其中31.70%的滑坡点落在低危险区，9.83%的滑坡点落在危险区，30.96%的滑坡点落在较高危险区，17.94%的滑坡点落在高危险区内（表2）。可见Monte Carlo-SHALSTAB模型有较大的应用潜力。

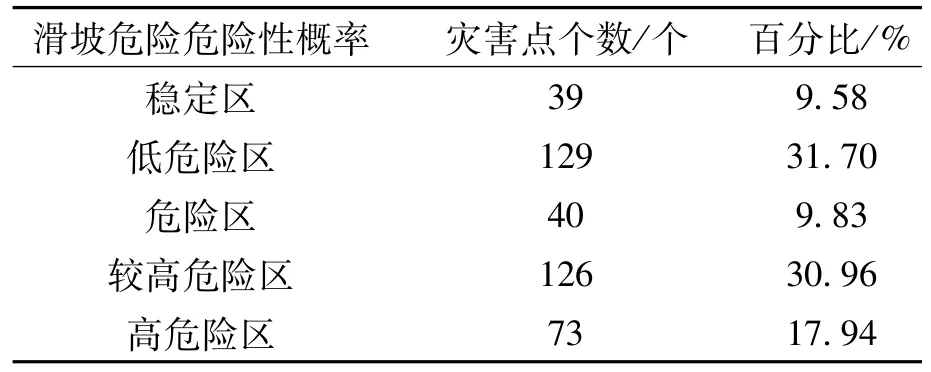
表2 不同危险性等级区域内的历史滑坡数量

4 结语

由于受到工作时间和经费等的限制，研究区域内的取样样本数量有限。并且岩土力学参数本身具有很强的空间不一致性，也难以获得精确的土壤力学参数的空间分布。如果仅仅赋予土壤力学参数一个值，可能导致预测的结果与实际情况有较大的差异。在考虑了岩土参数具有空间分布不确定性的特点，本研究提出了Monte Carlo-SHALSTAB模型。在已经岩土参数分布特征的基础上，该模型利用蒙特卡洛方法随机生成岩土参数值，利用SHALSTAB模型进行多次重复试验，计算每一个研究单元的安全系数，然后统计其失稳概率。

统计结果显示：当滑坡危险性阈值取10%时，有90%以上的历史滑坡点落在危险区域内；阈值为20%时，83.54%的滑坡点在危险区域内。为了使得更多的滑坡点在危险区域内，建议滑坡危险性阈值取10%，即认为当边坡失稳概率大于10%时，该格点属于危险区域，若该格点的边坡失稳概率小于10%，该格点属于安全区域。根据德化县内的407个已知的历史滑坡点资料，对Monte Carlo-SHALSTAB模型的滑坡危险性评价效果进行进一步的检验。有90%以上的滑坡灾害点落在危险区域内，其中31.70%的滑坡点落在低危险区，9.83%的滑坡点落在危险区，30.96%的滑坡点落在较高危险区，17.94%的滑坡点落在高危险区内。Monte Carlo-SHALSTAB模型物理意义明确，简易可行，评价结果与实况较吻合，其在滑坡危险性评价中具有较大的应用潜力。

［1］ 石菊松，石玲，吴树仁，等.滑坡风险评估实践中的难点与对策［J］.地质通报，2009，28（8）：1020-1030.

［2］ Ercanoglu M，Gokceoglu C.Assessmentof landslide susceptibility for a landslide-prone area（north of Yenice，NW Turkey）fuzzy approach［J］.Environmental geology，2002，41：720-730.

［3］ Beaza C，Corominas J.Assessment of shallow landslide susceptibility by means of multivariate statistical techniques［J］.Earth Surface Processes and Landforms，2001，26（12）：1251 -1263.

［4］ 殷坤龙，朱良峰.滑坡灾害空间区划及GIS应用研究［J］.地学前缘，2001，8（2）：279-284.

［5］ 王磊，张春山，杨为民，等.基于GIS的甘肃省甘谷县地质灾害危险性评价［J］.地质力学学报，2011，17（4）：388 -401.

［6］ 范强，巨能攀，向喜琼，等.证据权法在滑坡易发性分区中的应用［J］.灾害学，2015，30（1）：124-129.

［7］ 李秀珍，何思明，王震宇，等.降雨入渗诱发斜坡失稳的物理模型适用性分析［J］.灾害学，2015，30（1）：34-38.

［8］ 王旭春，何满潮，蒋宇静，等.在GIS中实现基于力学原理的滑坡稳定性计算［J］.岩石力学与工程学报，2003，22（6）：977-980.

［9］ 陈伟，许强，王新平.单体滑坡灾害危险性评价方法研究［J］.地球与环境，2011，39（4）：561-566.

［10］孙金山，陈明，左昌群，等.降雨型浅层滑坡危险性预测模型［J］.地质科技情报，2012，31（2）：117-121.

［11］康超，谌文武，张帆宇，等.确定性模型在黄土沟壑区斜坡稳定性预测中的应用［J］.岩土力学，2011，32（1）：207-210.

［12］王佳佳，殷坤龙，杜娟，等.基于GIS考虑准动态湿度指数的滑坡危险性预测水文-力学耦合模型研究［J］.岩石力学与工程学报，2013，32（Supp.）：3868-3877.

［13］Van Westen C J，Asch TW J，Soeters R.Landslide hazard and risk zonation-why is it still so difficult？［J］.Bulletin of Engineering Geology and the Environment，2006，37：1015-1022.

［14］Baecher G B，Christian JT.Reliability and statistics in Geotechnical engineering［M］.Wiley，2003：605.

［15］Chowdhury R，Flentje P，Bhattacharya G.Geotechnical slope analysis［M］.CRC Press，2010：737.

［16］Chowdhury R，Flentje P.Role of slope reliability analysis in landslide risk management［J］.Bulletin of Engineering Geology and the Environment，2003（62）：41-46.

［17］Griffiths D V，Huang J，Fenton G A.Probabilistic infinite slope analysis［J］.Computers and Geotechnics，2011（38）：577 -584.

［18］杨磊.基于概率方法的滑坡稳定性分析［J］.地下水，2005，27（5）：402-404.

［19］罗冲，殷坤龙，陈丽霞，等.万州区滑坡滑带土抗剪强度参数概率分布拟合及其优化［J］.岩石力学与工程学报，2005，24（9）：1588-1593.

［20］Chowdhuny R N.Slope Analysis［M］.New York：elsevier scientific publishing company，1978.

［21］Vanmarcke E H.Probabilistic modeling of soil profiles［J］.Journal of Geotechnical Engineering Division ASCE，1977：1227-1246.

［22］Wang Y，Cao Z，Au S.Efficient Monte Carlo Simulation of parameter sensitivity in probabilistic slope stability analysis［J］. Computers and Geotechnics，2010（37）：1015-1022.

［23］Park H J，Um J，Woo I，et al.Application of fuzzy set theory to evaluate the probability of failure in rock slope［J］.Engineering Geology，2012（125）：92-101.

［24］Hyuck-Jin P，Jung H L，Ik W.Assessment of rainfall-induced shallow landslide susceptibility using a GIS-based probabilistic ap-proach［J］.Engineering Geology，2013（161）：1-15.

［25］Raia S，AlvioliM，RossiM.Improving predictive power of physically based rainfall-induced shallow landslide models：a probabilistic approach［J］.Geoscientificmodel development，2014（7）：495-514.

［26］谢桂华.岩土参数随机性分析与边坡稳定可靠度研究［D］.长沙：中南大学，2009.

［27］Montgomery D R，Dietrich W E.A physically based model for the topographic control on shallow landsliding［J］.Water resource research，1994，30（4）：1153-1171.

［28］Wilkinson O L，Anderson M G，Lloyd D M.An integrated hydrologicalmodel for rain-induced landslide prediction［J］.Earth surface processes and landforms，2002（27）：1285-1297.

［29］Ko Ko C，Flentje P，Chowdhury R.Landslide qualitative hazard and risk assessmentmethod and its reliability［J］.Bulletin of Engineering geology and the environment，2004（63）：149-165.

［30］Fell R，Corominas J，Bonnard C，et al.Guidelines for landslides susceptibility，hazard and risk zoning for land use planning［J］. Engineering geology，2008（102）：85-98.

［31］中国地质环境监测院.区域降雨型地质灾害气象预警技术研究——“十一五”国家科技支撑计划重点项目课题成果之一［Z］.2010.

Assessment of Landslide Hazard Based on M onte Carlo-SHALSTAB M odel

Chen Yueli1，2，Chen Dehui2，Li Zechun1，3and Huang Junbao4
（1.College of Atmospheric Science，Nanjing University of Information Science＆Technology，Nanjing 210044，China；2.NumericalWeather Prediction Center，China Meteorological Administration，Beijing 100081，China；3.National Meteorological Center，Beijing 100081，China；4.Fujian Monitoring Center of Geological Environment，Fuzhou 350002，China）

Landslides are a common geological hazard during the rainy season in Dehua.The parameters of soilmaterials used in themodel of the hazard assessmenthave been identified as themajor source of uncertainty because of their spatial variability，so these parameters（such as cohesion and friction）are considered as random variables.This study proposes a probabilistic analysismethod to assess shallow landslide susceptibility by integrating an infinite slopemodel-SHALSTAB（SHAllow Landslide STABilitymodel）with GIS（Geographic Information System）and Monte Carlo simulation，taking into consideration the inherent uncertainty and variability in put parameters.The proposed approach is applied to assess the landslide hazard in Dehua to evaluate its feasibility.In the comparison with the historical landslides in Dehua，the probabilistic analysis showed that 90%of the observed landslides located in the risk area.Furthermore，31.70%of the historical landslides located in the lower-risk areas；9.83%of the historical landslides located in the dangerous areas；30.96%located in themore dangerous areas；17.94%located in themost dangerous areas.Themodel results show high accuracy basing on themodel verification and validation.

landslide；assessment of landslide hazard；Montecarlo；SHALSTABmodel

P642.22；X43

A

1000-811X（2015）04-0101-06

10.3969／j.issn.1000-811X.2015.04.020

陈悦丽，陈德辉，李泽椿，等.基于Monte Carlo-SHALSTAB模型的滑坡危险性评价——以福建省德化县为例［J］.灾害学，2015，30（4）：101-106.［Chen Yueli，Chen Dehui，Li Zechun，et al.Assessment of landslide hazard based on Monte Carlo-SHALSTABmodel［J］.Journal of Catastrophology，2015，30（4）：101-106.］*

2015-03-03 修回日期：2015-05-06

国家重点基础研究发展计划（2013CB430106）；中国气象局数值预报发展专项（GRAPES）

陈悦丽（1985-），女，河北平山人，博士生，主要从事地质灾害的气象预报研究.E-mail：aslongassun＠163.com

陈德辉（1955-），男，广西玉林人，博士，主要从事数值预报理论与数值模拟研究.E-mail：chendh＠cma.gov.cn