基于模型降阶的贝叶斯方法在三维重力反演中的实践

刘彦， 吕庆田， 李晓斌， 祁光，赵金花， 严加永， 邓震

1 中国地质科学院矿产资源研究所，国土资源部成矿作用与资源评价重点实验室， 北京 1000372 中国地质科学院地球深部探测中心， 北京 1000373 中国地质科学院地球物理地球化学勘查研究所， 河北廊坊 0650004 河南理工大学， 河南焦作 454000



基于模型降阶的贝叶斯方法在三维重力反演中的实践

刘彦1，2， 吕庆田2，3*， 李晓斌4， 祁光1，2，赵金花1，2， 严加永1，2， 邓震1，2

1 中国地质科学院矿产资源研究所，国土资源部成矿作用与资源评价重点实验室， 北京 1000372 中国地质科学院地球深部探测中心， 北京 1000373 中国地质科学院地球物理地球化学勘查研究所， 河北廊坊 0650004 河南理工大学， 河南焦作 454000

三维重力反演是地质工作者了解地球深部构造，认知地下结构的重要手段.按照反演单元划分，三维重力反演有离散多面体（Discrete）反演和网格节点（Voxels）反演两种方式.离散多面体反演由于易于吸收先验地质信息得到的理论场能够很好地拟合观测场，因此，在实际重力反演中更受欢迎.目前离散多面体重力反演中初始模型的建立方法繁杂不一，实际应用受到很大的限制.本文本着充分挖掘利用先验信息和重力观测数据得到丰富可靠的反演结果这一原则，以离散多面体反演技术为基础，改进建模过程.在初始模型的建立中，吸收贝叶斯算法优势，采用隐马尔科夫链改善朴素贝叶斯方法的分类效果，通过最大似然函数算法求解，再采取模型降阶技术，固定所建模型中几何体的形态或密度，达到在几何体形态（x,y,z）、密度（σ）和重力值（g）五个参数中降低维数目的，从而减小高维不确定性和正演的计算量，由此反演计算的地质体密度和分布范围相对更准确，更利于重现重力模型结构.通过单位球体和任意形态几何体模拟实验，以及安徽省泥河矿区三维重力反演实践，得到非常接近实际的密度或重力值，大幅提高了三维重力反演的精度和效率，说明该方法是有效、实用的.

三维重力反演；离散多面体模拟；贝叶斯方法；最大似然函数；模型降阶

1 引言

矿集区深部结构、构造关系以及成矿环境是控制矿床形成的直接因素，因此，无论对于成矿学还是深部资源勘查，厘清深部三维形态和物性（包括断裂延伸、岩体的空间展布以及与地层的相互关系）都十分重要.一直以来，地质工作者试图利用各种已知信息建立地下三维结构模型创造出多种方法，其中，以重力观测数据为基础以其他先验地质信息为约束的三维（3 Dimensional，简称3D）重力反演，已经成为了解地球深部结构的一种重要手段（Oldenburg et al.，1997，2007； Fullagar et al.，2000，2007； Williams et al.，2004； Welford and Hall，2007）.

按照反演单元划分，三维重力反演通常有网格节点（Voxels）和离散多面体（Discrete）两种方式（Li and Oldenburg，1998；姚长利，2002，2007）.离散多面体反演因其既易于吸收先验地质、构造（包括地层倾向、断层和矿化体等）信息，又可使反演的理论场与观测场误差较小而受到欢迎.对于地质信息约束下的三维重力反演，不少学者做过工作（Roy and Clowes，2000；Jessell，2001；Goleby et al.，2002；Malehmir et al.，2006，2009；Martin et al.，2007；Williams，2008；Wan et al.，2011；吕庆田等，2013）.综观过程，虽细节有所差别，但基本上可归纳为以下三步：①初始模型的建立，②反演的迭代与初始模型的升级，③模型的三维显示，其中步骤①和②至关重要.对于步骤①初始模型的建立，目前方法繁杂不一，尚未形成统一完美的解决方案，事实上，合理的初始模型能够减小后续重力反演的非唯一性，加快反演的收敛速度（McGaughey，2007；McInerney et al.，2007）.步骤②则是对步骤①的进一步优化，以获得符合观测数据的物性参数空间分布.

贝叶斯方法（Bayes，1763）最初主要用于统计学领域，1987年法国Tarantola教授在其基础上创立了贝叶斯反演理论（Tarantola，1987），之后，贝叶斯反演逐步应用于地球物理领域并得到广泛深化和应用（Green，1995；Scales and Snieder，1997；Gao，1997；Gouveia et al.，1998；Grandis et al.，1999；Lasses et al.，2004；Tarantola，2005；Khodja et al.，2010；Stuart，2010；Fernández-Martínez et al.，2013）.贝叶斯反演理论框架建立在概率论的基础上，它将数据信息与模型先验信息联系起来，通过模型的先验信息来约束模型的后验参数.由于贝叶斯推理把反演问题与观测数据信息、模型信息以及先验信息联系起来，使得求解约束泛函的极小点不需要计算梯度方向，因此，对约束项没有光滑性要求；同时，贝叶斯方法不只给出单一的反演值，而是给出解的后验分布采样，在此基础上得到解的条件期望、方差、置信区间等具有统计意义的结果，这使得贝叶斯方法能够很好地应用先验信息，得到丰富可靠的输出结果.将贝叶斯算法运用到三维重力反演中，应该有助于初始模型的改进.但是，在贝叶斯理论中，测量数据和先验信息包含在后验概率密度函数（PPD）中，它可以解释成模型的单点估计和不确定度等贝叶斯推断，这些信息的获取需要对反演问题进行优化求最优模型和在高维模型空间中对PPD进行采样积分；而且，从模型的后验概率密度函数中提取模型信息，需要计算它的模型估计、参数不确定度以及参数间的相关度等属性.所有这些，无疑会使贝叶斯方法受碍于维数，并且将为解决正演问题而付出高昂的计算成本.

为此，本文将开展以贝叶斯方法为基础的离散多面体三维重力反演研究，特别是在初始模型的建立中，吸收贝叶斯反演理论精华，将反演问题同观测数据、模型以及先验信息联系起来，计算中采用模型降阶技术克服反演的高维不确定性和复杂的正演成本，快速准确计算出地质体的密度和形态重现重力模型结构，再通过单位球体和任意形态几何体反演模拟实验以及安徽省泥河矿区应用实践，验证方法的正确性和实用性.

2 方法原理及实现过程

2.1 贝叶斯方法原理

如前所述，贝叶斯反演是综合利用未知模型参数的先验信息、实测数据以及由物理规律得到的正演模型等信息来反演模型参数，最后得到未知模型参数的后验概率分布函数及其相应的特征量.设m表示未知的M维模型参数空间，d表示N维数据空间，在贝叶斯反演中都看成是随机变量.实际应用中，数据d是已知的，模型参数化θ也是确定的，为了方便省略θ，得到贝叶斯公式（Carlin and Louis，2000）

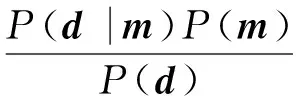
（1）

这时P（d）是常量，P（d|m）为已知数据d条件下随模型m变化的函数，称为似然函数，用L（m）表示.上式可以改写成

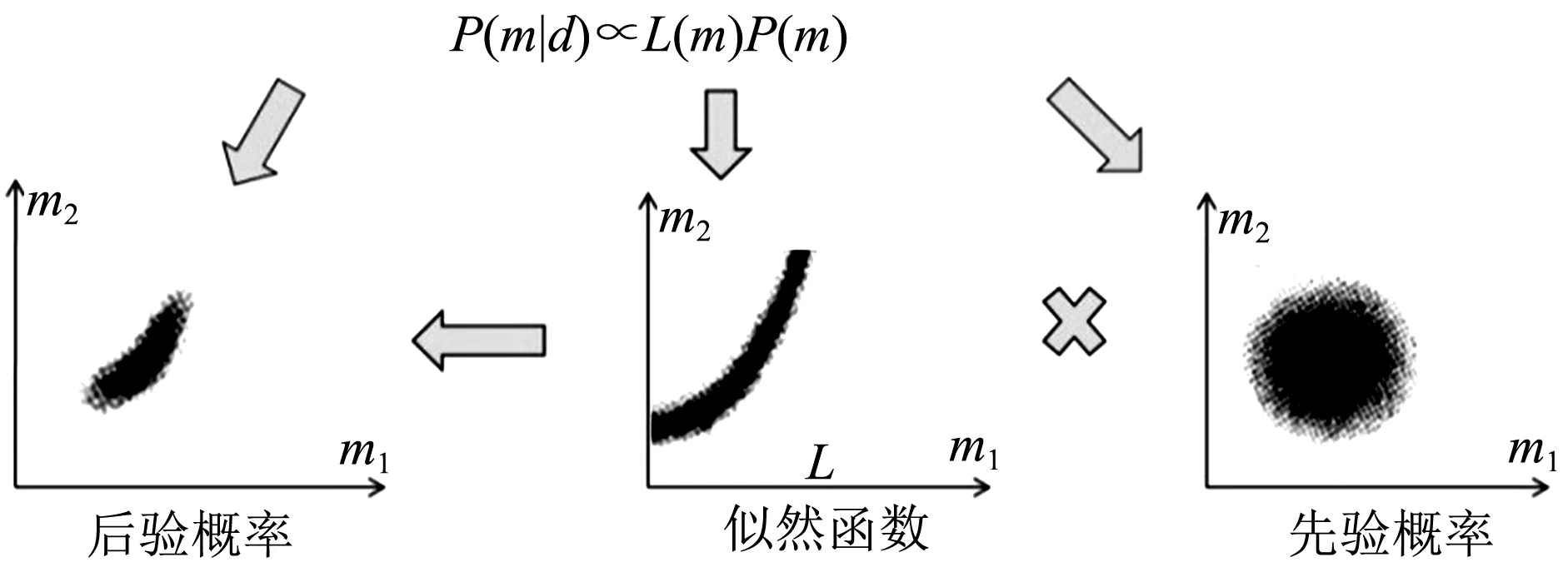
图1 贝叶斯方法原理

（2）

其中P（m|d）表示后验概率分布函数（PPD）.其原理可以简单概括如图1.

似然函数L（m）（或P（d|m））表达的是模型参数m与观测数据d之间的相对概率，在贝叶斯反演计算中，它的大小反映了模型响应与观测数据的适配程度，可见，似然函数L（m）是贝叶斯反演计算的关键参量，模型m的似然函数可以表示为（Scales and Snieder， 1997）

L（m）=

（3）

其中，g为正演算子（又称核函数），d为观测数据矢量，m为模型参数矢量，T表示转置，Cd为先验估计误差（以下公式中各参数皆如此）.

引入目标函数E（m），公式（3）似然函数L（m）可以改写为

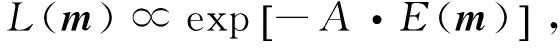
（4）

其中

（5）

A是一个比例因子.

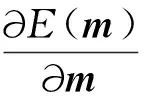
（6）

对应的协方差矩阵Cm为

（7）

可见，贝叶斯反演结果最终是由这个不确定度矩阵Cm和最大似然解mML共同定义，当数据误差服从Gaussian分布且是线性的，反演的结果也应满足Gaussian分布.实际反演通常存在欠参数化和超参数化两种情况：对于欠参数化情况，一般可采用贝叶斯信息准则（BIC）（Akaike，1980）来判断与数据信息一致的反演层数；对于超参数化情况，则采用倾向于简单结构的带先验信息反演，类似于正则化反演方法（TikhonovandArsenin，1977）.本文带先验信息的重力反演属于后者.

通常，重力观测数据或其他先验地质信息是有噪音的，反演的模型结果也会有误差，假定这些噪音和误差满足Gaussian分布，在重力反演中似然函数L（m）、模型的先验概率P（m）、目标函数E（m）可以类推表达如下：

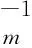
（8）

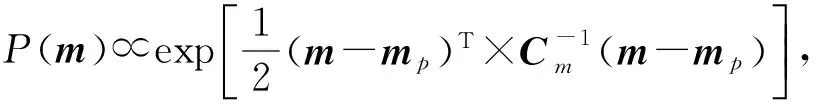
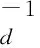
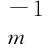
（10）

（11）其中（ξ,η,ζ）为地质体体积元的坐标，（x,y,z）为观测点的坐标，G为常数，等于6.672×10-11m3/（kg·s2）.

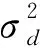
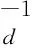
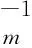
（12）

方程（12）的求解实质是加权二乘拟合，关键是在重力观测数据拟合（第一项）和先验估计（第二项）之间寻求一种折衷，其中权重系数的选取非常重要.权重系数越大，反演解越接近先验估计；反之，反演解越接近于不稳定的初始模型.常用方法有L-曲线法（Hansen，1992）和广义交叉法（Wahba，1990），详情参考文献（FarquharsonandOldenburg，2000；HaberandOldenburg，2000）.

2.2 三维重力反演过程

有了以上算法基础，以离散多面体为反演单元设计三维重力反演，包括：先验模型的确定、初始模型的建立、重力反演迭代与初始模型的升级、模型的三维显示，如图2所示.详情以下展开.

图2 三维重力反演流程图

2.2.1 准备数据、确定模型空间

收集已有信息、简化地质单元、测量岩石物性、电磁或地震剖面以及钻测井资料的综合解释等，定义建模区域.

2.2.2 根据已知先验信息采用贝叶斯算法建立初始模型，开展重力反演迭代与初始模型的升级

朴素贝叶斯分类（Naive Bayes Classifier，或NBC）是贝叶斯反演理论中的一种简单、稳定的分类算法，其思想是：对于给定的待分类项，求解在此项出现的条件下各个类别出现的概率，并按照概率最大划定待分类项的类别.建立朴素贝叶斯分类模型所需估计的参数很少，对缺失数据不太敏感，算法也比较简单，运用该方法对先验信息进行分类.考虑到通过朴素贝叶斯分类建立初始模型，无需了解模型参数之过程状态序列，只需计算模型参数最终状态的概率函数，因此，采用隐马尔可夫模型（Hidden Markov Model，或 HMM）更合适.设计如下主要流程：

第一步，确定模型参数特征属性及划分：根据先验信息p确定出模型参数矢量m.其中，模型参数矢量包括模型中各地质体的位置、埋深、厚度、密度等物理参数及其可能变化的范围.

第二步，获取所建模型体对应的观测向量数据作为训练样本：根据先验地质、地球物理信息和建模区域确定观测数据与地下物理模型参数之间的函数关系，即参入反演的核函数g.再由公式d=gm，通过核函数g（见公式11）与模型参数矢量m正演计算出所建模型体的观测向量数据d.

第三步，计算训练样本中每个类别的频率：将模型体生成的观测向量数据划分为不同的类别.

这里是根据先验信息推算模型区域每个地质体的最大似然解mML.对于重力贝叶斯反演，如公式（12）最大似然模型m的求解，涉及地质体坐标位置（ξ,η,ζ）、剩余质量（σ）和重力异常值（g）五个参数，计算维数较高，计算成本也高，而且影响反演解的收敛性增加不确定度.因此，借助模型降阶技术采用固定部分参数减小计算维数的方式，固定模型中地质体的坐标位置使得类别参数降到最少.这样，当体积确定时，根据“质量=密度×体积”，通过分段划分地质体与区域围岩的相对密度变化区间，等同于划分剩余质量的变化区间，再根据万有引力公式就可计算出模型地质体的重力异常数值范围.

第四步，计算这一位置固定的地质体的相对密度可能概率.

第五步，使用分类器鉴别所述模型地质体的最大似然解并将其分类.按照上述最大似然解算法，依据公式（12）计算模型，要求模型参数最大限度满足重力观测值与先验信息这一分类原则，确定模型中各个地质体（岩体）的坐标位置、埋深、厚度、密度等物理参数.

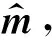
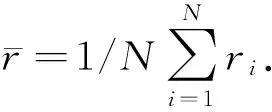
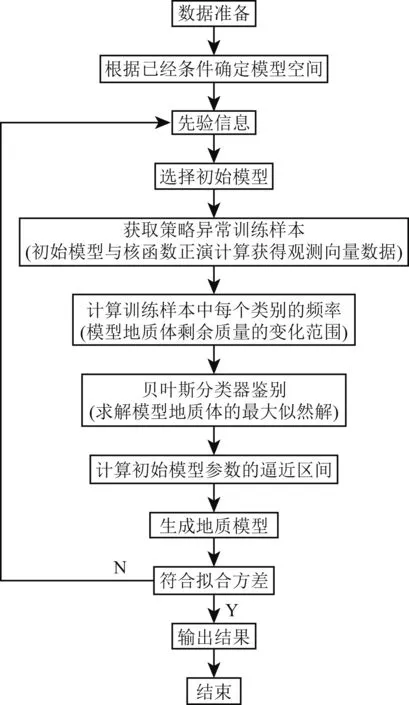
图3 贝叶斯算法程序

计算过程如图3所示，概括为：根据已知的先验信息选择初始模型；根据所选择的初始模型确定重力异常训练样本；计算训练样本中每个类别的频率（归结为计算模型中地质体剩余质量的变化区间）；通过贝叶斯分类器对观测向量数据进行分类鉴别（运用模型地质体的最大似然解），确定初始模型参数的逼近区间.若逼近区间符合模型重力与观测重力的拟合方差要求，则输出反演结果；若该逼近区间不符合拟合方差要求，则根据先验信息重新选择初始模型.通过上述六步，就可针对性地给出模型中各地质体的密度值和分布范围，得到较为准确的初始地质模型.具体程序见“基于贝叶斯反演理论的重力建模软件”（刘彦等，2015）.

2.2.3 采用离散体模拟方法将初始地质模型构建成2.5D地质模型

对每一个赋予初始密度的模型体，采用人机交互法修改建立2D剖面模型，完成建模区域内所有2D剖面的重力模拟后，将每条2D剖面的模型走向方向长度延长同剖面长度，初始模型变为2.5D地质模型.再对2.5D模型进行重力曲线拟合、模型修改处理，直到达到满意的数据拟合和获得合理的地质模型.可采用如澳大利亚EncomTechnologyPtyLtd.公司开发的专业软件EncomModelVisionProTM等重力数据处理、反演软件完成（祁光等，2012）.

2.2.4 将2.5D地质模型拼接拟合成3D地质模型

得到系列2.5D地质模型后，按照剖面的空间顺序依次将2.5D模型拼合成3D模型，计算3D模型的理论异常，并与实际异常对比，拟合误差较大的区域，需返回到2.5D剖面重新修改，如此调整得到3D地质模型.

2.2.5 对3D地质模型进行可视化和结构解译处理

采用三维可视化模拟软件（如：GOCAD或EncomPA）对3D地质模型进行可视化和结构解译处理，经过可视化及结构解译处理后的模型能够形象直观地反映地下三维密度结构.

3 模拟实验

为验证上述贝叶斯算法开展重力反演的有效性，选择单位球体和任意形态几何体两种模型体开展模拟实验.重力值可依据牛顿万有引力定律计算，球体的计算公式为（曾华霖，2005）

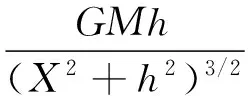
（14）

其中Δg为球体的重力异常值，其单位取μGal，1μGal=10-8m·s-2，G为万有引力常量，取值6.672×10-11m3/（kg·s2），M为场源质量，h为场源中心深度或埋深，R为球体半径，X为观测平面上测点到场源中心的水平距离，这里指测线距离，h、R、X的单位均为m，σ为模型体相对围岩的密度差或相对密度，单位为kg·m-3.对于任意形态几何体，可通过三角剖分法将其划分成若干个极小单元的四面体，根据这些最小单元四面体底面中心点的坐标（x，y，z）与三角形面积计算每个四面体的体积，再与密度乘积得到四面体的质量.为简化计算，任意形态几何体剖分至百个数量级单元体，剖分得到的小四面体近似于单位质量球体，重力异常值可采用公式（14）来计算，最后对所有剖分体的重力异常值求和，得到任意形态几何体的重力异常总值.

3.1 单位球体数值模拟

以单位球体为例，测点到场源中心的水平距离X和埋深h为固定值，采用上述贝叶斯算法，计算球体的密度范围.假设单位球体处于测点坐标X0=1000 m处，埋深h0为800 m（如图4a所示），球体与围岩的相对密度（即密度差）σ为30 kg·m-3，测线总长2000 m，测点间距为10 m，加入正态分布的观测噪声，依据公式（14）正演计算得到重力观测值，如图4b所示.

采用设计的贝叶斯算法程序经过10次迭代运算误差小于0.02，满足精度要求，得到模型的相对密度值为31.7578125±5.2734375 kg·m-3，运算过程如表1所示.再采用隐马尔科夫链分类器鉴别的反演计算，得到模型与围岩的相对密度值为30.3107438614098 kg·m-3，方差为1.87447932360261×10-5，更接近实际密度差30 kg·m-3.可见，隐马尔科夫链分类器鉴别的贝叶斯反演结果相对更准确.

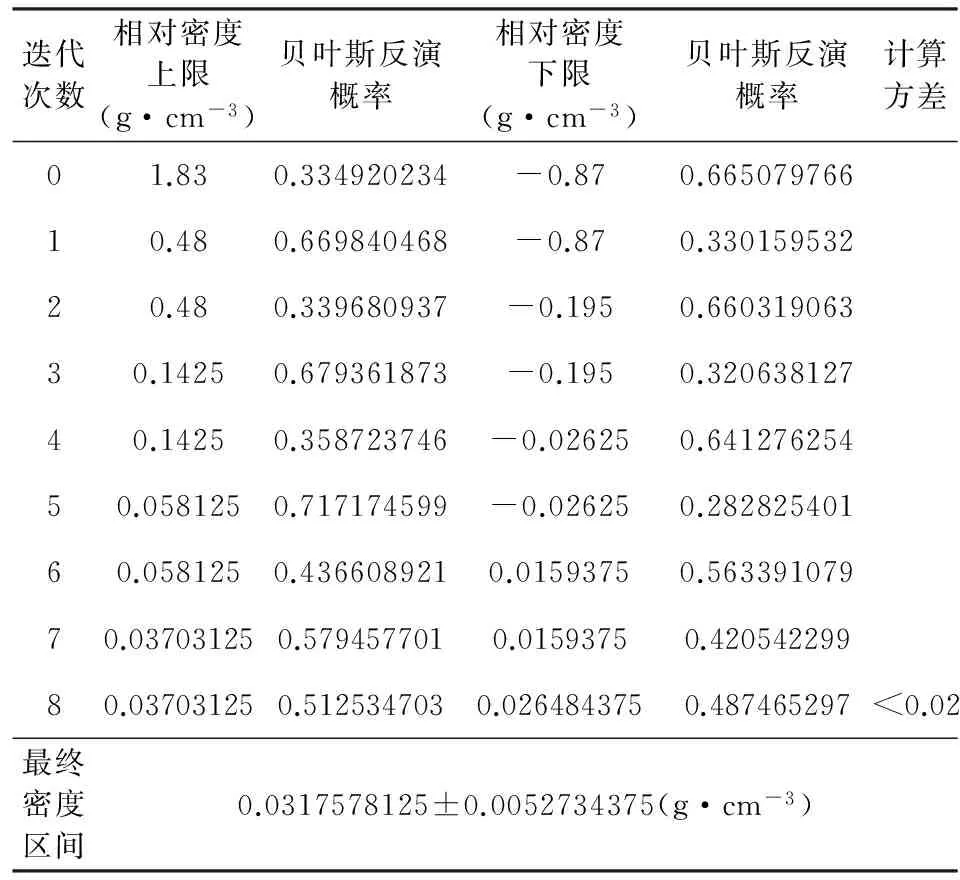
表1 单位球体模拟贝叶斯计算结果Table 1 Bayesian calculation results of unit sphere simulation

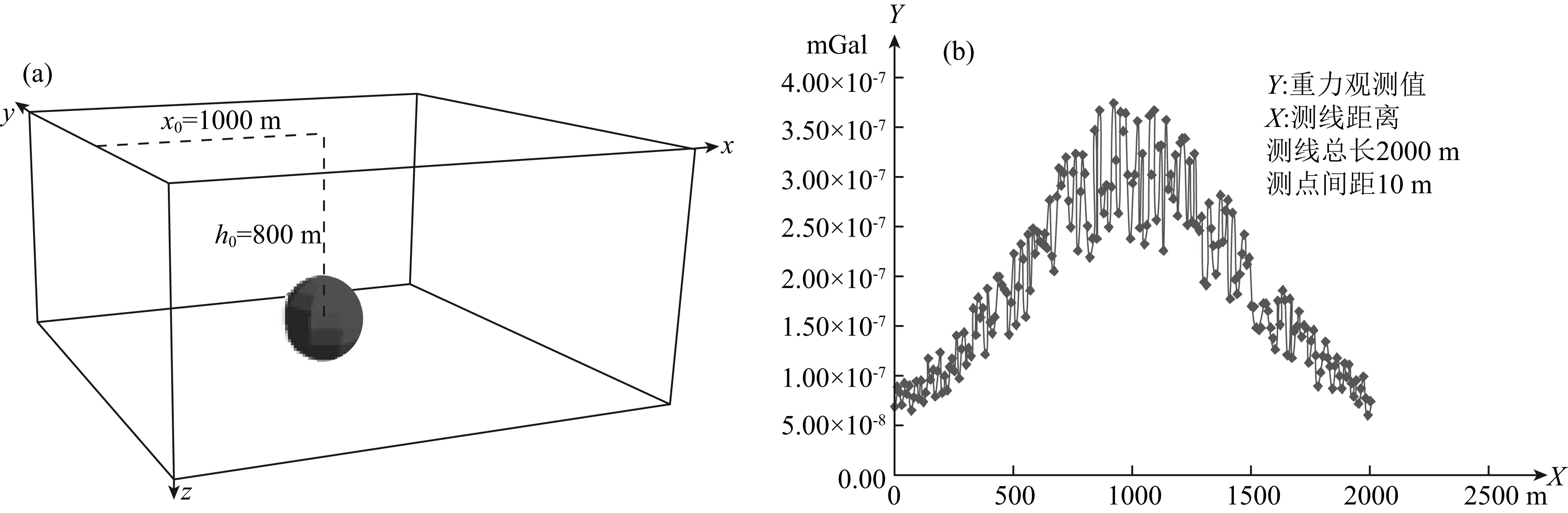
图4 单位球体数值模拟示意图

3.2 任意形态几何体数值模拟

选择与围岩的相对密度σ为30 kg·m-3的任意形态几何体正演计算重力数据.为贴近实际，几何体定义为长轴a等于300 m、短轴b等于30 m的透镜体，三角剖分后如图5a所示.透镜体位于测点坐标X0=1000 m处，埋深h0为800 m，测线总长2000 m，测点间距为10 m.加入正态分布的噪声，正演计算得到的重力值如图5b所示.

同样，采用上述贝叶斯算法程序计算，经过10次迭代运算误差小于0.02，满足精度要求，得到相对密度值为31.7578125±5.2734375 kg·m-3，计算结果与单个球体相同.可见多个球体叠加运算对于贝叶斯算法影响并不大，同时也证明贝叶斯算法具有一定的稳定性，对梯度方向没有要求.采用隐马尔科夫链分类器鉴别反演计算，得到剩余密度值为30.0626173207599 kg·m-3，方差为1.72748273715972×10-5，结果与实际给定的相对密度30 kg·m-3非常接近，说明本文设计的贝叶斯反演方法对复杂形体同样有效.

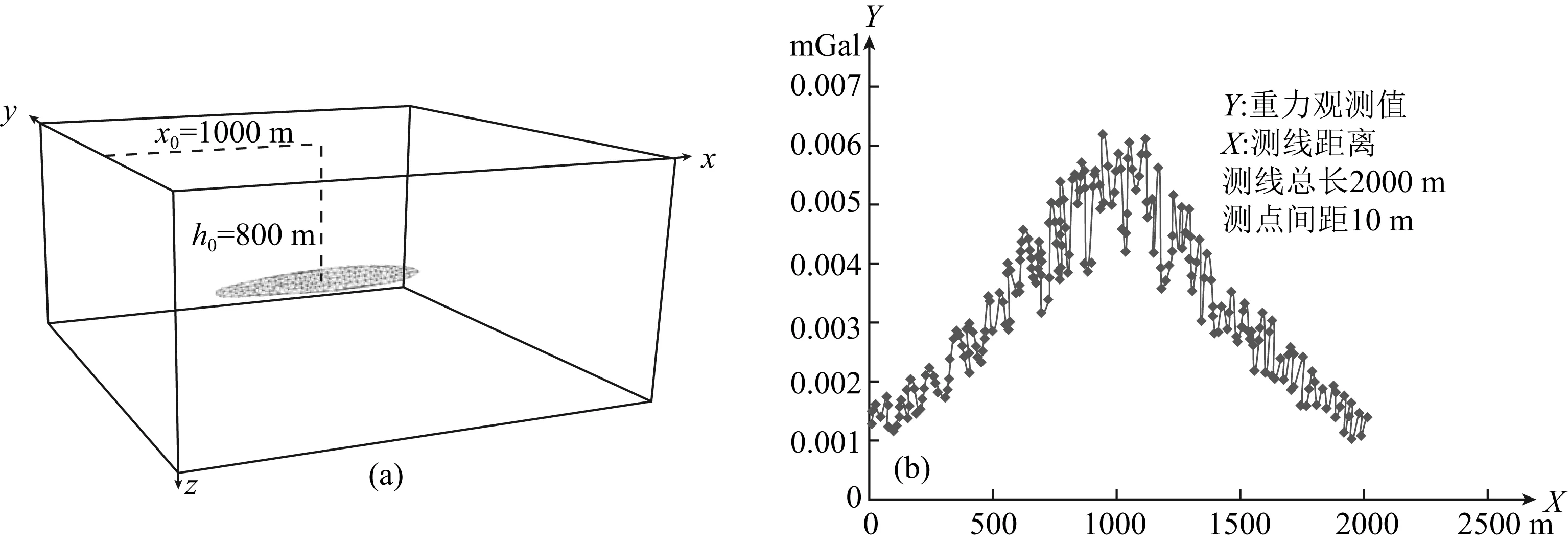
图5 任意形态几何体数值模拟示意图

4 安徽泥河矿区三维重力反演实践

泥河矿床位于安徽省庐枞火山岩盆地西北边缘，是长江中下游地区实施第二空间找矿以来在庐枞矿集区500～1500 m深度范围内最先发现的大型“玢岩型”铁矿床.矿区处于罗河—黄屯北东向成矿带上，南西距罗河铁矿床3 km，北东距龙桥铁矿床13 km（吴明安等，2011）.泥河深部矿体的发现引起众多的关注，由此产生一系列关于“玢岩型”铁矿床成矿与控矿模式以及如何区分矿体与非矿体异常的思考.欲解决这些关乎找矿成败的关键问题，需要精细解剖地球物理异常性质，深入认识矿区深部结构，明晰区域地质状况.

早在2007年初，高锐等在庐枞矿集区及外围布设两个剖面总长达153.28 km的十字形深地震反射测线（高锐等，2010），2008年吕庆田等部署两条穿过泥河、罗河、大包庄等主要矿体的10 km长的地震剖面测线（吕庆田等，2010），2009—2010年吕庆田等又在庐枞地区完成5条总长达326 km的深地震反射剖面（吕庆田等，2014，2015），这些反射地震成像很好地显现出矿区所在区域的深部构造.不仅如此，针对泥河矿床更是实施完成不少具体工作：吴明安（2011）总结了泥河铁矿的发现过程及区域找矿方向，赵文广（2011）查明矿床的地质特征并分析了成因，认为辉石闪长玢岩是泥河铁矿的成矿母岩，正长斑岩穿切火山岩地层和矿体，是成矿期后形成的脉岩；刘彦（2012）、祁光（2012）以泥河矿床为例开展了基于重力异常分离方法寻找深部隐伏铁矿的实践以及地质信息约束下的三维重磁建模工作；张昆（2014）开展了音频大地电磁、可控源音频大地电磁、瞬变电磁和复电阻率四种电磁法探测试验，获得泥河铁矿区三维电性结构模型；范裕（2014）开展了矿床成岩成矿年代学研究，认为泥河铁矿床的成岩成矿作用几乎同时发生，盆地内130 Ma左右的辉石闪长玢岩侵入体是寻找泥河式玢岩型铁矿床的勘探靶区；张舒（2015）分析测试了泥河铁矿主成矿期矿石矿物的稀土元素、硫同位素及铅同位素，认为泥河铁矿是由次火山岩体演化产生的含矿高温热液在闪长玢岩穹窿顶部，通过交代充填作用形成的玢岩型铁硫矿床；张明明（2014）以钻孔资料为依据，采用离散光滑插值法建立成矿岩体的精细三维模型，重现闪长玢岩体的形态特征；周涛发（2014）则系统总结了泥河铁矿床的地质地球化学特征，提出泥河矿床的形成除了与辉石闪长玢岩有关外，还与三叠系膏盐层有着重要的成因关系，并建立起泥河铁矿床两期成矿模式.有了以上深入细致的工作，泥河矿区结构与成矿控矿特征渐趋明朗，积累了大量宝贵的资料，这些信息资料是三维重力反演试验成功的重要保证.

利用收集到的资料和数据如上述设计程序开展矿区三维重力反演，通过试验效果检验方法的效力.资料包括：1∶10000地形地质图， 1∶50000高精度重力观测数据，74个钻孔累计8.33万米的钻井资料（含69个钻孔测井数据），882块钻孔岩芯物性测试数据，以及庐枞矿集区5条电磁剖面和9条地震剖面.

首先简化地质单元，提取重要信息.将1∶10000地形地质图简化（见图6），泥河矿区存在第四系（Q）砂砾岩、白垩统杨湾组（K1y）砂岩、白垩统双庙组（K1sh）和白垩统砖桥组（K1zh）火山岩4套地层.地层产状平缓，褶皱不发育，往深部地层产状略有起伏变化.构造简单，仅有火山岩地层的北西倾斜单斜构造和成矿期后的浅层断裂.需要重点关注的是，泥河铁矿体主要赋存在闪长玢岩体的顶部与砖桥组下段的火山碎屑岩中，闪长玢岩体的穹状隆起部位是赋矿的有利构造（吴明安等，2011；赵文广等，2011）.

接着备好数据，确定模型空间.重力资料采用1∶50000高精度观测数据（源自安徽省地质调查院），需开展位场分离工作保留剩余重力值（刘彦，2012）.反演区域是在综合矿区地层、岩体及整体结构并充分考虑到钻孔资料可明确的1200 m岩性深度这些已知信息基础上划定的.建模2D剖面部署如图6方框内线条所示，平面面积为5.6 km2（2.8 km×2.0 km），剖面垂直构造走向取北偏西40°方向，间距为100 m，共划分28条平行剖面，区域重力场的背景密度设为2.62 g·cm-3.

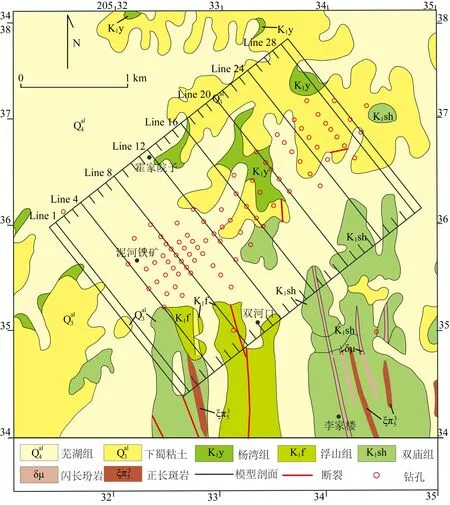
图6 泥河矿区地质简化图

运用贝叶斯反演程序建立初始模型.采用离散多面体建模需要依次对每条剖面开展重力反演工作.以矿区9线剖面为例，依据已有地质信息、钻孔资料以及电磁地震等认识，勾画出先验模型如图7a所示，该先验模型基本界定地质体的坐标位置和埋深，这等同于固定地质体的体积.再计算各地质体的密度区间，采用刘彦等（2015）设计的贝叶斯反演程序.结合测试的882块物性数据，给出各地层和岩体的密度区间范围，利用程序快速算出初始模型中各地质体的密度（见表2），省却常规离散体反演建模过程中反复调试密度的困顿，可大大提高建模效率.从地表起由上至下，第四系砂砾岩（Q）密度为2.10±0.03 g·cm-3，白垩统杨湾组（K1y）地层密度为2.30±0.05 g·cm-3，白垩统双庙组上段（K1sh2）地层密度为2.55±0.04 g·cm-3，白垩统双庙组下段（K1sh1）地层密度为2.57±0.03 g·cm-3，白垩统砖桥组（K1zh）地层密度为2.65±0.03 g·cm-3；其它岩体及矿体的密度范围：闪长玢岩（δμ）岩体密度为2.90±0.04 g·cm-3，磁铁矿（Mt）、黄铁矿（Py）以及石膏矿（Ah）密度分别是3.48±0.09 g·cm-3、3.35±0.09 g·cm-3、2.93±0.07 g·cm-3.

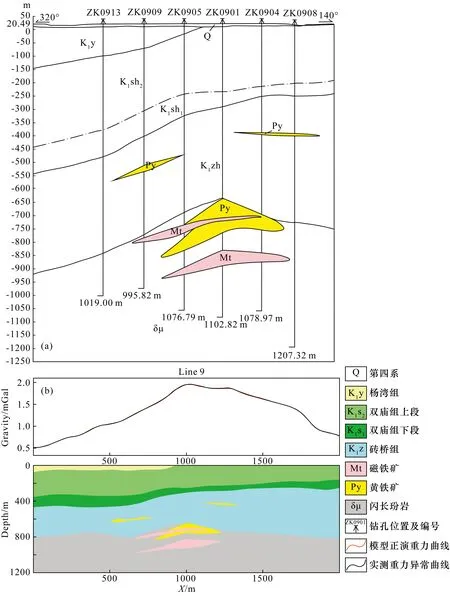
图7 泥河矿区9线剖面重力反演示意图

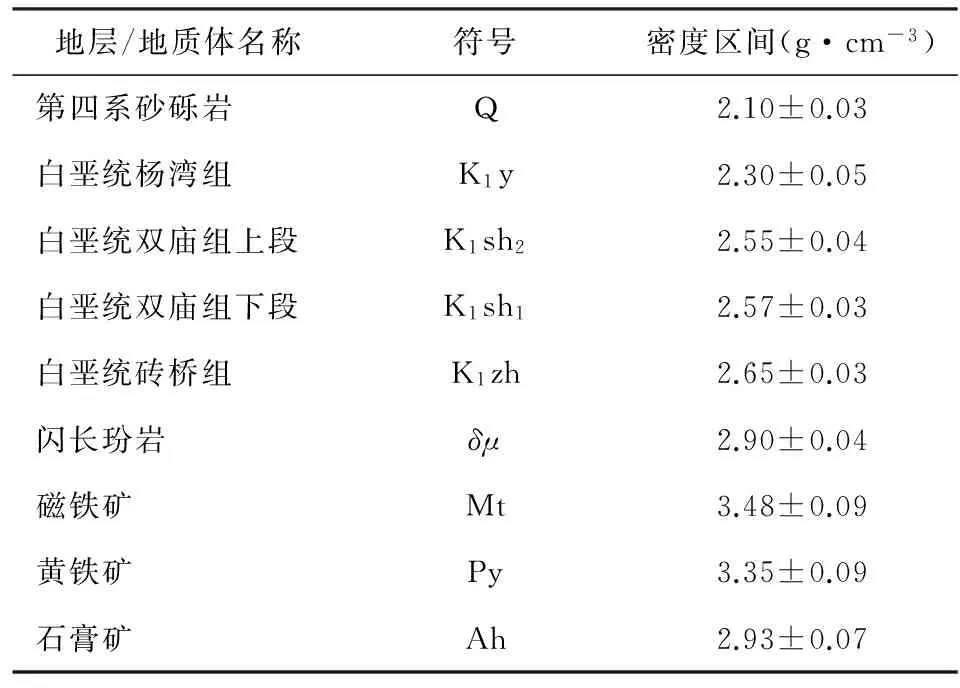
表2 采用贝叶斯计算的泥河矿区初始模型中各地质体的密度

2.5D模型的构建.有了确定的密度区间再调整修改地质体的形态，即进行重力的反演迭代与初始模型的升级，直到模型曲线和实际重力曲线拟合完好，此时模型生成的重力值与实际重力观测值方差满足允许范围，由此建立剖面的2.5D初始模型（如图7b所示）.同样方式，依次做好全部28条剖面的重力反演迭代与初始模型的升级工作.

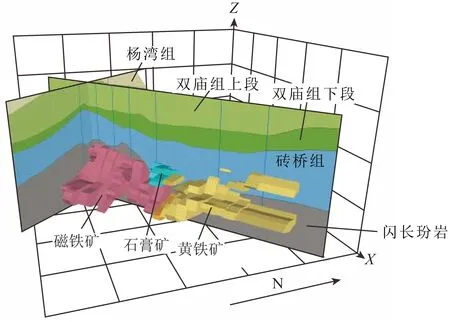
图8 安徽省泥河矿区三维重力反演模型

3D模型的生成与显示.选用离散多面体反演建模专业软件Encom ModelVision ProTM拼接拟合，完成整个泥河矿区的三维重力反演.反演最后得到的模型加载到三维可视化专业软件Encom PA，实现多方位成像和结构解译，最终模型如图8所示.

图8所示的3D模型显示：泥河矿区内的主要矿体为磁铁矿、黄铁矿以及石膏矿；矿体整体呈北东向展布，延伸至东北部时矿体稍有抬升；矿区磁铁矿、黄铁矿较多，石膏矿相对较少；磁铁矿主要位于矿区的西南部，呈透镜状；黄铁矿主要集中在矿区的东北部，中部少量的石膏矿；黄铁矿和石膏矿埋深相对于磁铁矿较浅，矿体深度大致在地下600～1100 m范围内.矿区东北部矿体主要是垂直方向上的两层黄铁矿，上层矿体体积较小，呈层状分布，矿体在西南部较小，东北部较大，平均宽度约为245 m，埋深约为600 m，厚度约40 m；下层矿体体积较大，呈透镜状，埋深在800～1050 m，最大宽度约为680 m.三维重力反演结果还揭示出泥河矿床的控矿特征：矿区内地层由浅到深主要为第四系盖层（Q）、白垩统杨湾组（K1y）、白垩统双庙组（K1sh）和白垩统砖桥组（K1zh）；较浅层的黄铁矿和石膏矿多位于砖桥组上段地层，体积较小，呈层状似层状分布；矿体主要集中在砖桥组下段侵入岩中，侵入岩主要为辉石闪长玢岩和脉岩；侵入体顶面形成隆起，矿区西南部隆起陡立，矿区东北部隆起宽缓.该模型刻画展示的矿体和岩体的空间关系，与吴明安（2011）、赵文广（2011）等运用地质学，范裕（2014）等运用成矿年代学，周涛发（2014）、张舒（2015）等运用地球化学，张明明（2014）等运用离散光滑插值法，张昆（2014）等运用电磁法等推论结果吻合一致，说明本方法开展三维重力反演是实用有效的.

5 结论与认识

（1） 本文发挥离散多面体反演技术和贝叶斯方法优势，通过理论分析、综合研究，设计程序完成模型试验和矿区实践，改进了传统的三维重力反演方式，得到如下认识：将贝叶斯方法引入重力反演初始模型的建立中，可以定量地利用已知先验信息、观测数据以及物理规律来确定模型参数具体数值，节省模型选择时间，提高反演效率；最大似然函数算法应用于分类器的鉴别中改善了传统朴素贝叶斯分类方法，采取模型降阶技术固定所建模型中几何体的形态或密度，达到在几何体形态、密度和重力值五个参数中降低维数，可以减小高维不确定性和正演的计算量，有利于降低多解性，提高反演的准确度；任意形态几何体模拟试验以及泥河矿区反演实践证明，这种基于贝叶斯算法的三维重力反演方式，能够充分吸收先验信息，改善反演精度，提高建模效率.

（2） 重点主要集中于改善反演初始模型的建立方式，三维重力反演的实现是通过本次设计的贝叶斯方法模块与其它成熟反演建模软件（如：Encom ModelVisionProTM）整合完成的.在贝叶斯反演计算中，可以通过固定密度、变化体积这种方式准确圈定出异常体的展布形态，这对于实际勘探生产将更具有应用价值.

致谢 本文得到中国地质大学（北京）薛涛老师及学生张永强的大力支持和帮助，审稿专家富有建设性的意见对于本文的完善起了很好的作用，稿件修改期间还得到中国地质科学院矿产资源研究所史大年研究员的指导以及与四川大学周永道博士的有益探讨，所有这些一并致谢！

Akaike H. 1980. Likelihood and the Bayes procedure. Bernardo J M, DeGroot M H, Lindley D V , et al eds.Bayesian Statistics. Valencia:University Press, 141-166.

Carlin B P, Louis T A. 2000.Bayes and Empirical Bayes Methods for Data Analysis.2nd ed. New York:Chapman & Hall.

Dosso S E, Wilmut MJ. 2006. Data uncertainty estimation in matched-fieldgeoacousticinversion.IEEEJournalofOceanicEngineering, 31（2）: 470-479. Farquharson CG, Oldenburg DW. 2000. Automatic estimation of the trade-off parameter in nonlinear inverse problems using the GCVand L-curve criteria. 70th SEG Program Expanded Meeting.Expanded Abstracts, 265-268.

Fernández-Martínez J L, Fernández-Muiz Z, Pallero J L G, et al. 2013.From Bayes to Tarantola: New insights to understand uncertainty in inverse problems.JournalofAppliedGeophysics, 98（11）: 62-72.

Fullagar P K, Hughes N A, Paine J. 2000. Drilling-constrained 3D gravity interpretation.ExplorationGeophysics, 31（2）: 17-23.

Fullagar P K, Pears G A. 2007. Towards geologically realistic inversion. Milkereit Bed. Proceedings of the Fifth Decennial Conference on Mineral Exploration.ExpandedAbstracts, 445-460.

Gao R, Lu Z W, Liu J K, et al. 2010. A result of interpreting from deep seismic reflection profile: Revealing fine structure of the crust and tracing deep process of the mineralization in Luzong deposit area.ActaPetrologicaSinica（in Chinese）, 26（9）: 2543-2552.

Gao S. 1997. A Bayesian nonlinear inversion of seismic body-wave attenuation factors.Bull.Seism.Soc.Am., 87（4）: 961-970.

Goleby B R, Korsch R J, FominT, et al. 2002. Preliminary 3-D geological model of the Kalgoorlie region, YilgarnCraton, Western Australia, based on deep seismic-reflection and potential-field data.AustralianJournalofEarthSciences, 49（6）: 917-933.

Gouveia W P, Scales J A. 1998. Bayesian seismic waveform inversion: Parameter estimation and uncertainty analysis.J.Geophys.Res., 103（2）: 2759-2779.

Grandis H, Menvielle M,Roussignol M. 1999. Bayesian inversion with Markov chains：The magnetotelluricone-dimensional case.GeophysicalJournalInternational, 138（3）: 757-768.

Green P J. 1995. Reversible jump Markov chain Monte Carlo computation and Bayesian model determination.Biometrika, 82（4）: 711-732.

Haber E, Oldenburg D. 2000. A GCV based method for nonlinear ill-posed problems.ComputationalGeosciences, 4（1）: 41-63.

Hansen PC. 1992.Analysis of discrete ill-posed problems by means of the L-curve.SIAMReview, 34（4）: 561-580.

Jessell M. 2001. Three-dimensional geological modelling of potential-field data.Computers&Geosciences, 27（4）: 455-465.

Khodja M R, PrangeM D, DjikpesseH A. 2010. Guided Bayesian optimal experimental design.InverseProblems, 26（5）: 055008.

Lasses M, Siltanen S. 2004. Can one use total variation prior for edge-preserving Bayesian inversion?.InverseProblems, 20（5）: 1537-1563.

Li Y G, Oldenburg D W. 1998. 3-D inversion of gravity data.Geophysics, 63（1）: 109-119.

Liu Y, Yan J Y, Wu M A, et al. 2012. Exploring deep concealed ore bodies based on gravity anomaly separation methods: A case study of the Nihe iron deposit.ChineseJ.Geophys.（in Chinese）, 55（12）: 4181-4193, doi: 10.6038/j.issn.0001-5733.2012.12.030.

Lü Q T, Han L G, Yan J Y, et al. 2010. Seismic imaging of volcanic hydrothermal iron-sulfur deposits and its hosting structure in Luzong ore district.ActaPetrologicaSinica（in Chinese）, 26（9）: 2598-2612.

Lü Q T, Qi G, Yan J Y. 2013. 3D geologic model of Shizishan ore field constrained by gravity and magnetic interactive modeling: A case history.Geophysics, 78（1）: B25-B35.

Lü Q T, Liu Z D, Tang J T, et al. 2014. Upper crustal structure and deformation of Lu-Zong ore district: Constraints from integrated geophysical data.ActaGeologicalSinica（in Chinese）, 88（4）: 447-465.

Lü Q T, Liu Z D, Yan J Y, et al. 2015.Crustal-scale structure and deformation of Lu-Zong ore district: Joint interpretation from integrated geophysical data.Interpretation, 3（2）: SL39-SL61.

Malehmir A, Tryggvason A, Juhlin C, et al. 2006. Seismic imaging and potential field modelling to delineate structures hosting VHMS deposits in the Skellefte Ore District, Northern Sweden.Tectonophysics, 426（3-4）: 319-334.

Malehmir A, ThunehedH,Tryggvason A. 2009. The paleoproterozoic Kristineberg mining area, northern Sweden: Results from integrated 3D geophysical and geologic modeling, and implications for targeting ore deposits.Geophysics, 74（1）: B9-B22.

Martin L, PerronG, MassonM. 2007. Discovery from 3D visualization and quantitative modelling. Milkereit Bed.Proceedings of the Fifth International Conference on Mineral Exploration.ExpandedAbstracts, 543-550.

McGaughey J. 2007. Geological models, rock properties, and the 3D inversion of geophysical data. MilkereitBed.Proceedings of Exploration: Fifth Decennial International Conference on Mineral Exploration. Expanded Abstracts, 473-483.

McInerney P, Goldberg A, Calcagno P, et al. 2007. Improved 3D geology modelling using an implicit function interpolator and forward modelling of potential field data. MilkereitBed.Proceedings of Exploration 2007: Fifth Decennial International Conference on Mineral Exploration. Expanded Abstracts, 919-922.

Mitsuhata Y. 2004. Adjustment of regularization in ill-posed linear inverse problems by the empirical Bayes approach.GeophysicalProspecting, 52（3）: 213-239.

Oldenburg D W, Li Y G, Ellis R G. 1997.Inversion of geophysical data over a copper gold porphyry deposit: A case history for Mt. Milligan.Geophysics, 62（5）: 1419-1431.

Oldenburg D W, Pratt D A. 2007.Geophysical inversion for mineral exploration: A decade of progress in theory and practice. MilkereitBed.Proceedings of Exploration Fifth Decennial International Conference on Mineral Exploration. Expanded Abstracts, 61-95.

Qi G, LüQT, Yan J Y, et al. 2012.Geologic constrained 3D gravity and magnetic modeling of Nihe deposit-Acasestudy.ChineseJ.Geophys. （in Chinese）, 55（12）: 4194-4206, doi: 10.6038/j.issn.0001-5733.2012.12.031.

Roy B, Clowes R M. 2000. Seismic and potential-field imaging of the Guichon Creek batholith, Brithsh Columia, Canada, to delineate structures hosting porphyry copper deposits.Geophysics, 65（5）: 1418-1434. Scales J A, Snieder R. 1997.To Bayes or not to Bayes?Geophysics, 62（4）: 1045-1046.

Stuart A M. 2010. Inverse problems: A Bayesian perspective.ActaNumerica, 19: 451-559.

Tarantola A. 2005. Inverse Problem Theoryand Methods for Model Parameter Estimation.Philadelphia, PA:SIAM. Tikhonov A N, Arsenin V Y. 1977. Solutions of Ill-posed Problems.Washington, DC: John Wiley & Sons, Inc.Wahba G. 1990. Spline Models for Observational Data.Philadelphia, PA:Society of Industrial and Applied Mathematics.Wang G W, ZhangS T, Yan C H, et al. 2011. Mineral potential targeting and resource assessment based on 3D geological modeling in Luanchuan region,China.Computers&Geosciences, 37（12）1976-1988.

Welford K J, HallJ. 2007. Crustal structure of the Newfoundland rifted continental margin from constrained 3-D gravity inversion.GeophysicalJournalInternational, 171（2）: 890-908.

Williams N C, Lane R, Lyons P. 2004.Regional constrained 3D inversion of potential field data from the Olympic Cu-Au province, South Australia.ASEGExtendedAbstracts,（1）: 1-4.

Williams N C. 2008.Geologically-constrained UBC-GIF gravity and magnetic inversions with examples from the Agnew-Wiluna greenstone belt, Western Australia[Ph. D. thesis]. Vancouver,Canada: The University of British Columbia.Wu M A, Wang Q S, Zheng G W, et al. 2011. Discovery of the Nihe iron deposit in Lujiang, Anhui, and its exploration significance.ActaGeologicaSinica（in Chinese）, 85（5）: 802-809.

Yang W C. 1997.Theory and Methods in Geophysical Inversion （in Chinese）.Beijing: Geological Publish House.

Yao C L, Hao T Y,Guan Z N. 2002.Restrictions in gravity and magnetic inversions and technical strategy of 3D properties inversion.Geophysical&GeochemicalExploration（in Chinese）, 26（4）: 253-257.

Yao C L, Zheng Y M,Zhang Y W. 2007. 3-D gravity and magnetic inversion for physical properties using stochastic subspaces.ChineseJournalofGeophysics（in Chinese）, 50（5）: 1576-1583, doi: 10.3321/j.issn:0001-5733.2007.05.035.

Zeng H L. 2005. Gravity Field and Gravity Exploration （in Chinese）.Beijing: Geological Publish House.

Zhang K, Yan J Y, Lü QT, et al.2014.The electromagnetic exploration experimentation of Nihe porphyry iron ore in anhui.ActaGeologicaSinica（in Chinese）, 88（4）:498-506.

Zhang M M, Zhou T F, Yuan F, et al. 2014.Three-dimensional morphological analysis method for mineralization related intrusion and prospecting indicators of nihe iron deposit in luzong basin.ActaGeologicaSinica（in Chinese）, 88（4）：574-583.

Zhang S, Wu M A, Zhao W G, et al. 2014.Geochemistry characteristics of Nihe iron deposit in Lujiang, Anhui Province and their constrains to ore genesis.ActaPetrologicaSinica（in Chinese）, 30（5）:1382-1396.

Zhao W G, Wu M A, Zhang Y Y, et al. 2011. Geological characteristics and genesis of the Nihe Fe-S deposit, Lujiangcountry, Anhui province.ActaGeologicaSinica（in Chinese）, 85（5）: 789-801.

Zhou T F, Fan Y, Yuan F, et al.2014.The metallogenic model of nihe iron deposit in Lu-Zong basin and genetic relationship between gypsum-salt layer and deposit.ActaGeologicaSinica（in Chinese）, 88（4）:562-573.

附中文参考文献

范裕,刘一男,周涛发等.2014.安徽庐枞盆地泥河铁矿床年代学研究及其意义.岩石学报，30（5）:1369-1381.

高锐,卢占武,刘金凯等．2010.庐枞金属矿集区深地震反射剖面解释结果-揭露地壳精细结构，追踪成矿深部过程. 岩石学报,26（9）:2543-2552.

刘彦, 严加永, 吴明安等. 2012. 基于重力异常分离方法寻找深部隐伏铁矿—以安徽泥河铁矿为例. 地球物理学报, 55（12）: 4181-4193, doi: 10.6038/j.issn.0001-5733.2012.12.030.

刘彦,张永强等．2015. 基于贝叶斯反演理论的重力建模程序软件．中华人民共和国国家版权局：软著登字第1044862号．

吕庆田,韩立国,严加永等. 2010. 庐枞矿集区火山气液型铁、硫矿床及控矿构造的反射地震成像．岩石学报，26（9）:2598-2612.

吕庆田,刘振东,汤井田等. 2014. 庐枞矿集区上地壳结构与变形：综合地球物理探测结果. 地质学报, 88（4）: 447-465.

祁光, 吕庆田, 严加永等. 2012. 先验地质信息约束下的三维重磁反演建模研究—以安徽泥河铁矿为例. 地球物理学报, 55（12）: 4194-4206, doi: 10.6038/j.issn.0001-5733.2012.12.031. 吴明安, 汪青松, 郑光文等. 2011. 安徽庐江泥河铁矿的发现及意义. 地质学报, 85（5）: 802-809.

杨文采. 1997. 地球物理反演的理论与方法. 北京: 地质出版社.

姚长利, 郝天珧, 管志宁. 2002. 重磁反演约束条件及三维物性反演技术策略. 物探与化探, 26（4）: 253-257.

姚长利, 郑元满, 张聿文. 2007. 重磁异常三维物性反演随机子域法方法技术. 地球物理学报, 50（5）: 1576-1583, doi: 10.3321/j.issn:0001-5733.2007.05.035.

曾华霖. 2005. 重力场与重力勘探. 北京: 地质出版社.

张昆,严加永,吕庆田等.2014.安徽泥河玢岩铁矿电磁法探测试验.地质学报,88（4）:498-506.

张明明,周涛发,袁锋等.2014.庐枞盆地泥河铁矿床成矿岩体三维形态学分析及找矿指标研究.地质学报,88（4）:574-583.

张舒,吴明安,赵文广等.2014.安徽庐江泥河铁矿矿床地球化学特征及其对成因的制约.岩石学报,30（5）:1382-1396.

赵文广, 吴明安, 张宜勇等. 2011. 安徽省庐江县泥河铁硫矿床地质特征及成因初步分析. 地质学报,85（5）:789-801.

周涛发,范裕,袁峰等.2014.安徽庐枞盆地泥河铁矿床与膏盐层的成因联系及矿床成矿模式.地质学报,88（4）:562-573.

（本文编辑 刘少华）

3D gravity inversion based on Bayesian method with model order reduction

LIU Yan1，2, LÜ Qing-Tian2，3*, LI Xiao-Bin4, QI Guang1，2, ZHAO Jin-Hua1，2, YAN Jia-Yong1，2, DENG Zhen1，2

1InstituteofMineralResourcesChineseAcademyofGeologicalSciences,MLRKeyLaboratoryofMetallogenyandMineralAssessment,Beijing100037，China2ChinaDeepExplorationCenter—SinoProbeCenter,ChineseAcademyofGeologicalSciences,Beijing100037,China3InstituteofGeophysicalandGeochemicalExplorationChineseAcademyofGeologicalSciences,HebeiLangfang065000，China4HenanPolytechnicUniversity,HenanJiaozuo454000，China

3D gravity inversion is an important way for geologist to understand the deep structure of earth. As the key part of 3D gravity inversion, inversion unit includes discrete simulation and voxels. In fact discrete simulation inversion method is welcome, which is easy to absorb prior geological information, and can make the theory gravity field fitting observation gravity field. This paper summarizes the problems of discrete simulation inversion method in 3D gravity inversion and improves its modeling process. In order to build an initial accurate model, we develop the feature of Bayesian inversion theory. The algorithm of maximum-likelihood function is used and hidden Markov chain is added to build a naive Bayes classifier. Based on probability theory, Bayesian method can relate measure data into the priori information, and constrain posterior parameters through the prior information model. While the priori information is fully utilized, output results is abundant and reliable. In the process of Bayesian method, model order reduction techniques are taken to reduce parameter dimension with fixing the model body geometry shape or density in the five parameters of geometry shape （x,y,z）, density （σ） and gravity （g）.Thereby high-dimensional uncertainty and the forward calculation are also decreased. As density and distribution of geological body can be accurately obtained, gravity model structure is fine also. To test the method of 3D gravity inversion based on those Bayes algorithm, simulation experiments of unit sphere and any geometry with normal distribution noise carry on, and 3D gravity inversion experiment of Nihe mining area in Anhui province have performed. The density and gravity value of inversion calculation is very close to the reality. It is proved that the Bayesian method is practical and effective.

3D gravity inversion； Discrete body simulation； Bayesian method； Maximum-likelihood function； Model order reduction

“十二五”国家科技支撑计划课题（2011BAB04B01）,国家深部探测专项（SinoProbe-03）,国家自然科学基金项目（41304100）,中国地质调查项目（12120114019401）,中央级公益性科研院所基本科研业务费专项资金项目（K1317）联合资助.

刘彦，女，1975年生，高级工程师，理学博士，主要从事地球物理勘探技术和深部探测工作.E-mail：liuy@cags.ac.cn

*通讯作者 吕庆田，男，1964年生，研究员，博士生导师.主要从事深部探测和金属矿勘查技术方法研究.E-mail：lqt@cags.ac.cn

10.6038/cjg20151233.

10.6038/cjg20151233

P631

2015-02-12，2015-10-10收修定稿

刘彦， 吕庆田， 李晓斌等. 2015. 基于模型降阶的贝叶斯方法在三维重力反演中的实践.地球物理学报，58（12）:4727-4739,

Liu Y, Lü Q T, Li X B, et al. 2015. 3D gravity inversion based on Bayesian method with model order reduction.ChineseJ.Geophys. （in Chinese）,58（12）:4727-4739,doi:10.6038/cjg20151233.