音频大地电磁法强干扰压制试验研究

2015-06-25汤井田刘子杰刘峰屹肖晓李晋张林成谢勇

地球物理学报 2015年12期

关键词：时间段电阻率波形

汤井田，刘子杰，刘峰屹，肖晓＊，李晋，3，张林成，谢勇

1中南大学有色金属成矿预测与地质环境监测教育部重点实验室，长沙 410083

2中南大学地球科学与信息物理学院，长沙 410083

3湖南师范大学物理与信息科学学院，长沙 410081

4长沙航空职业技术学院，长沙 410124

1 引言

大地电磁法（Magnetotelluric，MT）自20世纪50年代提出以来，经过几十年的发展其在理论方法、仪器设备等方面都取得了长足的进步（魏文博，2002），目前已经成为一种重要的地球物理勘探方法.音频大地电磁法（Audio Magnetotelluric，AMT）是在MT的基础上提出来的，其工作方法、观测参数与MT基本相同；AMT的场源为天然音频电磁场，频率较MT高（李金铭，2005）.由于天然场具有信号微弱、极化方向随机等特点（考夫曼和凯勒，1987），极易受到其他电磁噪声的干扰.因此在大地电磁法的发展过程中，噪声压制一直是地球物理学者所关注的问题.为此国内外研究人员提出了一系列的方法，比如互功率谱法、Robust估计、远参考方法、小波变换、经验模态分解（Empirical Mode Decomposition，EMD）等等（Goubau et al.，1978；Gamble et al.，1979；Egbert and Booker，1986；范翠松等，2008；范翠松，2009），这些方法对压制非相关噪声取得了一定的效果，但也存在一定的问题，如经过远参考处理之后的数据误差棒变大，Robust估计无法消除输入端噪声且对近源噪声去除效果不佳（汤井田等，2012b），小波变换严重依赖于其基函数的选取，EMD无法揭示每时段的频率特性和能量差异所具有的细微性变化，分解得到的固有模态函数（IMF）具有多分辨性（汤井田等，2012b）等.特别是在矿集区，噪声干扰通常为相关噪声，具有强度大、类型复杂等特点，这些方法基本上没有效果.因此目前针对矿集区强干扰噪声的压制仍然存在一定的局限性，需要进一步进行研究解决.

针对矿集区存在的强干扰，课题组进行了较深入的研究，提出了数学形态滤波的方法，并运用到实测MT数据的去噪处理中，取得了明显效果.本文在此基础上，将数学形态滤波和阈值法相结合，应用于含有强干扰噪声的AMT数据处理中，开展了实际试验.以“已知”的含噪数据和“无噪”数据为基础进行时间域去噪处理，从多方面对处理结果进行分析评价.结果表明：结构元素恰当的数学形态滤波方法可以对人工源强干扰进行识别、去除，阈值法则可以消除形态滤波后的脉冲干扰，二者结合可以有效压制AMT中的强干扰噪声，提高数据可靠性.

2 试验数据

试验地区位于四川省西昌市境内，图1为具体的野外试验布置图.图中AB为人工发射源，长度1.2km.1、2、3线为CSAMT的3条测线，ASY0002B为AMT试验点，距离发射源约1.2km.经现场踏勘和调查，AMT试验点周围无明显电磁干扰源，对该点AMT数据的分析和处理结果（图3）也表明其受到的干扰很小，可以作为试验的参考点.试验仪器为加拿大凤凰公司的MTU－5A和V8发射系统.

AMT数据采集中采用“十”字形布极方式，一组电极平行于AB，另一组与之垂直，磁棒布置在不同的象限内（图1）.在人工源发射源的工作期和间歇期，连续地采集电磁场信号，记录时间域的电磁场波形，总观测时间约2.9h，其中受发射源干扰的时间有两个时间段，共计约1.3h.发射源长度1.2km，按频率表自动地发送不同频率（8192～0.125Hz）的方波电流，共计31个频率，低频电流约20A，高频电流约7A.数据采集过程中有雷电现象发生.

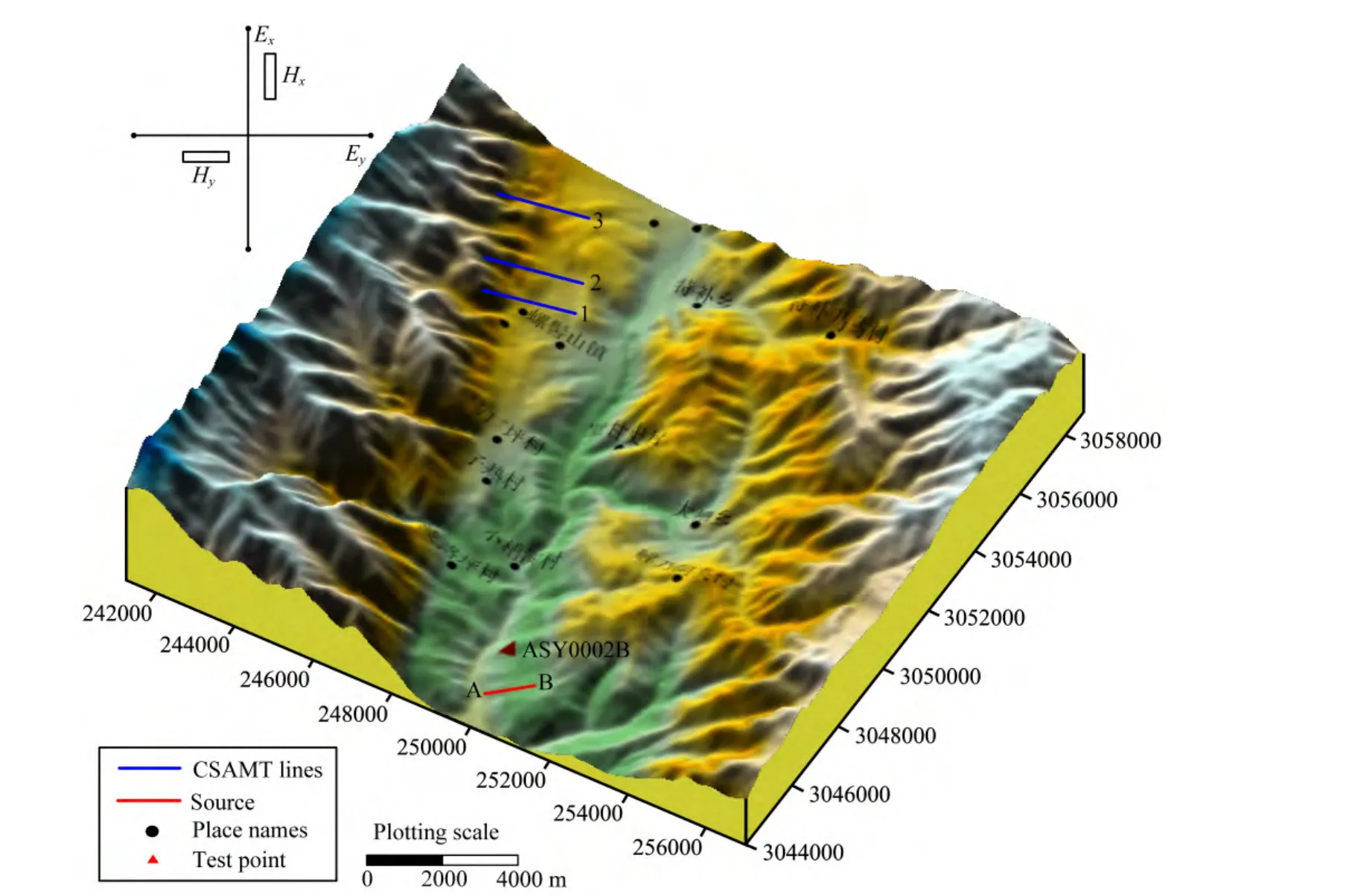
图1 测点ASY0002B野外布置图（坐标轴单位为m）Fig.1 The field layout at site ASY0002B

图2、3分别为试验点电磁场的时间域波形和估计的视电阻率－相位曲线.由图2a可以看出，在发射源的间歇期，电磁场时间域波形类似于平稳的随机信号，且振幅小、能量弱，具备天然场信号的特征.其中存在的一些脉冲干扰，其幅值小，且无规律性可言，属于随机干扰，可能是近区雷电及游散电流所致.图2b为发射源工作期的电磁场时间域波形，其中存在明显的大尺度、周期性的类阶跃波和类充放电波形，且能量强，振幅大，正常的天然场信号基本被完全淹没，极大降低了信噪比.虽然我们并不能准确地界定天然电磁场的波形及特征，但这类振幅大、波形规则、有一定周期性的电磁场显然不会是天然的电磁场信号.经与图2a及发射源记录的电流波形对比，可以确认这类电磁场应该是人工源的强电磁干扰.需要说明的是，图2a显示的虽然是TS4（采样率150Hz）中记录的低频信号，但TS3（采样率2400 Hz）和TS2（采样率24000Hz）中记录的中高频段数据中同样存在类似的干扰，只是因发射电流小，其强度较低频的弱.

图3为测点的视电阻率－相位曲线.由图3a可以看出，测点的视电阻率和相位曲线在中、低频（约200Hz以下）受到了严重的干扰，曲线存在大量“飞点”，数据离散，连续性差，形态不明确，相位受到的干扰情况较视电阻率弱；在XY方向，其视电阻率在200Hz左右出现严重脱节，在200～3Hz频段其出现整体抬升，而在3～0.35Hz其大体形态呈约45°上升趋势；相位曲线在3Hz以下呈现整体下掉趋势，多数频点趋近于0°，与CSAMT中的近区效应相同；在YX方向，自200Hz以下视电阻率和相位曲线跳变严重，无基本形态.其高频段受干扰较小，曲线比较光滑，形态明确，只是在1000Hz左右由于处于“死频带”范围之内（Garcia and Jones，2005），YX方向的视电阻率曲线连续性相对较差.图3b为无人工源干扰时间段的视电阻率－相位曲线，在该时间段内曲线比较连续、光滑，数值稳定，低频相对来说存在一些轻微跳变，这可能是由于存在的随机干扰的影响，处于“死频带”内的视电阻率出现“飞点”、连续性相对较差.

值得注意的是，图3a中高于200Hz的视电阻率及相位曲线光滑、连续、误差棒小，与图3b中相同频段的曲线特征相似，基本没有受到人工源信号的畸变.对于本次试验，收发距为1.2km，该地区的高频电阻率约120Ωm，200Hz的电磁波的趋肤深度约为360m，基本处于发射源的远区.因此，可以认为，对于处于发射源远区的高频段AMT数据，即使电磁场波形受到影响，但视电阻率和相位也基本不受影响.因此，在压制强干扰的各种处理中，可以只对中低频段的数据进行处理.

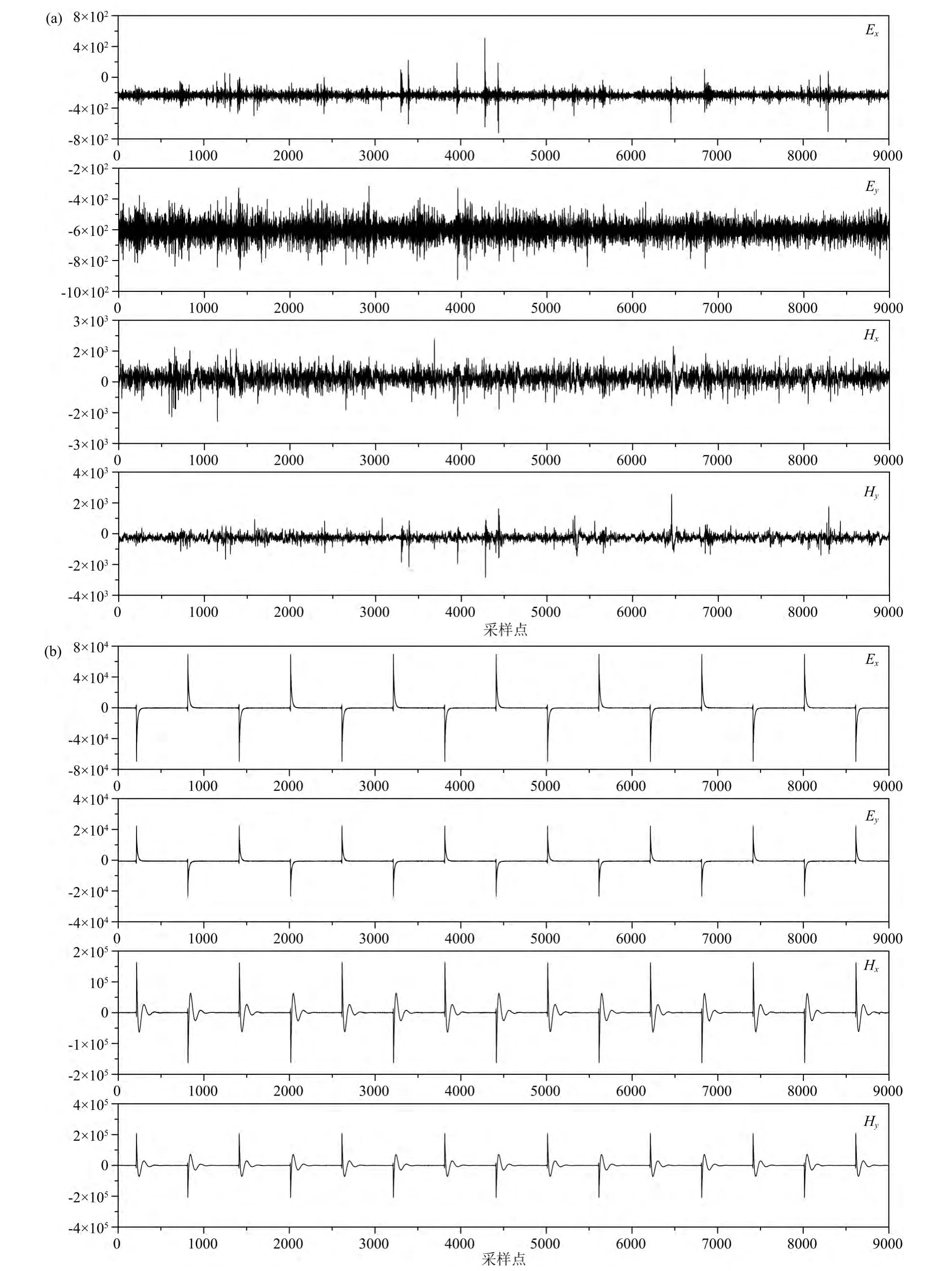
图2 测点ASY0002B时间域波形（采样率为150Hz）（a）未受人工源干扰时间段；（b）受人工源干扰时间段.纵轴为振幅，下同.Fig.2 Time series segments with a sampling rate of 150Hz at site ASY0002B（a）A segment without controlled－source noise；（b）A segment include controlled－source noise.

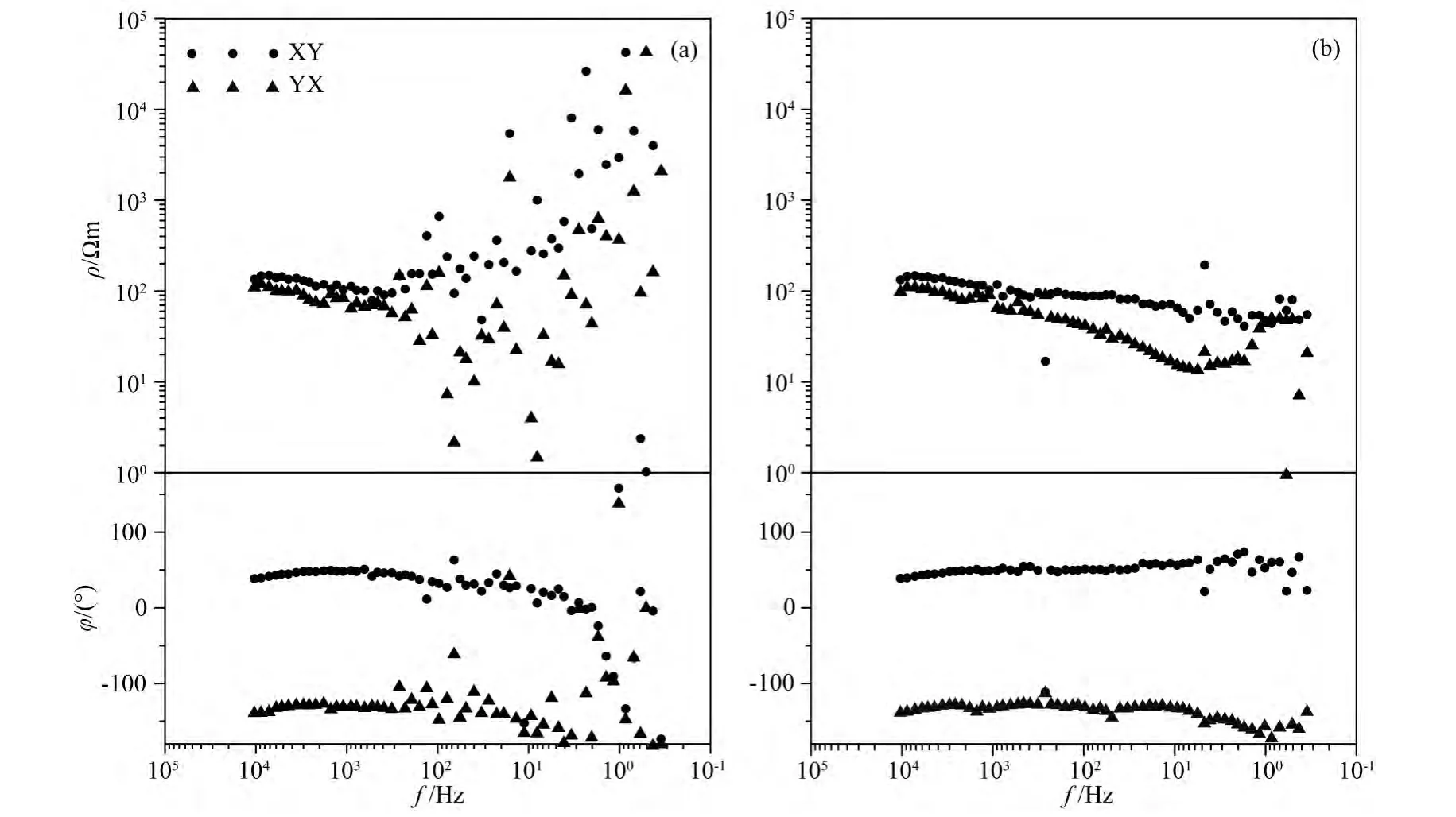
图3 测点ASY0002B视电阻率－相位曲线（a）全时段；（b）无人工源干扰时间段.Fig.3 Apparent resistivity and phase curves at site ASY0002B（a）Calculated by all collecting data；（b）Calculated by data segment without controlled－source noise.

3 人工源压制方法和效果评价

此次试验工作是在课题组对MT信号研究工作的基础上开展的，在以前的处理过程中只是利用数学形态率波进行处理，并没有与其他处理手段相结合.针对此次的AMT试验数据，由于噪声强度大，经形态滤波之后保留了大量的脉冲干扰，因此作者利用阈值法对脉冲信号进行去除，这是此次处理相对于以往MT处理中的不同之处.通过前文对人工源干扰的分析可知，AMT数据的中低频数据受到了严重的干扰，而高频数据由于位于远区，受到干扰较小，因此在时间去噪处理过程中，只处理中低频数据，高频数据仍采用原始数据，以保证数据的可靠性.针对处理效果，作者利用视电阻率－相位曲线、频谱、极化方向等多个参数进行了评价.

3.1 数学形态滤波

数学形态滤波（Mathematical Morphology Filtering）是一门综合了多种学科的交叉学科，近些年广泛应用于信号处理方面.其基本思想是通过集合来描述目标信号，通过各个部分之间的联系说明目标信号的结构特点，从而设计合适的结构元素来提取有效信息，利用其对信号几何特征的匹配或修正，同时保留目标信号的主要形状，以达到抑制去除干扰噪声的目的.通过课题组和前人的研究结果表明，数学形态滤波针对典型大尺度强干扰有较好的抑制能力，其方法运算简单、快速，可并行计算（汤井田等，2012a，b；李晋，2012；汤磊等，2013）.有关该方法的详细原理和处理步骤可参阅李晋博士论文（2012），在此不再赘述.

由于形态滤波是基于信号的形状对信号进行处理的，每个采样点的结果取决于相应信号的采样点及其临界值，因此在进行去噪处理过程中，结构元素的选取是十分关键的一步.选择合适的结构元素的类型和尺寸能较好地获取噪声信号的轮廓，还原天然场信号的原始特征.在课题组以往对MT信号的研究中发现（汤井田等，2012a，b，c；李晋，2012），抛物线型的结构元素对充放电型的强干扰有较好的识别效果，重构的MT信号较平稳，且保留了丰富的细节成分.针对此次实验数据的信号特征，由于其强干扰类型主要为充放电干扰，不存在其他类型的强干扰，且相对于 MT信号，AMT信号的频率较高，所以在结构元素宽度的选择上较MT的小，因此在结构元素的选取方面作者采用宽度合适的抛物线型结构元素.在进行处理的过程中，由于在可控源发送机未工作的时间段内其时间域信号平稳，除了受到少量脉冲干扰之外，并未受到其他强干扰，因此作者只针对受人工源干扰时间段进行处理，未受人工源干扰的时间段仍采用原始数据，以进一步提高数据的可靠性.图4与图5分别为测点受人工源干扰时间段经三点和五点抛物线型结构元素数学形态滤波处理之后的时间域信号，选取的时间段与图2b相同.对比三点和五点抛物线型滤波结果可以看出：相对于原始信号，二者都对大尺度的噪声干扰进行了有效压制，都可基本消除干扰波形的形态，但三点抛物线型的处理效果相比于五点抛物线型较好，干扰噪声幅值降低为原始信号的1／3，这是由于五点抛物线型结构元素宽度较大，对干扰波形的轮廓不能有效识别，造成信号失真度增大，所以在此作者采用三点抛物线型滤波结果.需要说明的是，由于目前形态滤波的处理方法还没有实现结构元素的自适应选取，因此在处理过程中采用统一的三点抛物线型结构元素进行处理.因为时间域的干扰为不同频率的充放电噪声干扰，其在时间域信号中的宽度也不相同，这就导致部分噪声经过处理之后在其边缘保留了脉冲干扰，且幅值相对于正常信号较大.

此外，由于数学形态滤波的滤波效果主要取决于结构元素的类型和长度，而在实测AMT数据中往往会存在多种类型的噪声干扰，不会如试验数据一样干扰单一、明确，因此需要根据具体的干扰类型和强度进行分析.针对不同类型的干扰需要选取合适的结构元素类型，其应与干扰波形存在一定的相似性，比如矩形元素对类方波干扰有较好的识别效果，而三角波干扰则可选取三角形结构元素进行压制等；对于结构元素的长度则需根据干扰波形宽度进行选取，其长度应小于或等于干扰波形长度，而其长度过大时有可能无法获得干扰波形的轮廓，致使信号失真.

3.2 阈值法

针对经过形态滤波之后部分信号存在的脉冲干扰，需要利用阈值法去除，进一步降低噪声干扰的强度，提高信噪比.在阈值的选取方面，需要经过反复试验以获得更为理想的效果.图6和图7分别为选取不同阈值处理之后的时间域波形，阈值处理前的数据采用三点抛物线型结构元素滤波结果，与图4、图2b的选取时间段相同.对比二者可以看出，选取全时段的时间域信号绝对值的算数平均值作为阈值对脉冲信号的压制效果较好，由于干扰波形的幅值与天然场相距非常大，若采用干扰时间段的均值作为阈值则其保留的脉冲干扰仍得不到有效压制.因此作者最后采用全时段信号绝对值的算术平均值作为阈值，针对大于阈值的信号采用阈值代替，其他仍保留原值.可以看出，此时对于图4中存在的脉冲信号得到了很好地压制，从中提取到了正常稳定的天然场信号.

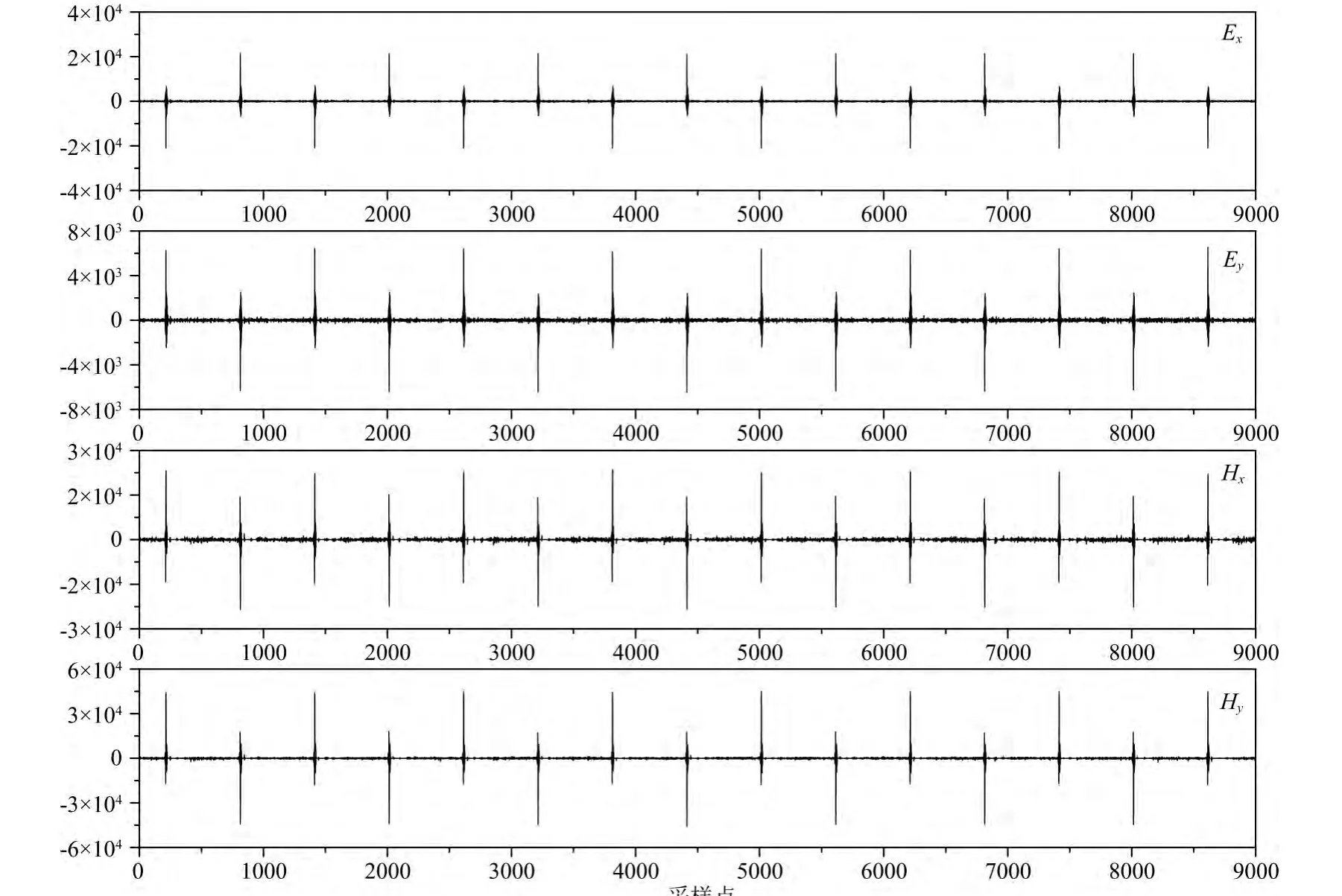
图4 测点ASY0002B受人工源干扰时间段经三点抛物线型结构元素形态滤波后的时间域波形（采样率为150Hz）Fig.4 Mathematical morphology with 3points parabola processing result of time series segments including controlled－source noise with a sampling rate of 150Hz at site ASY0002B

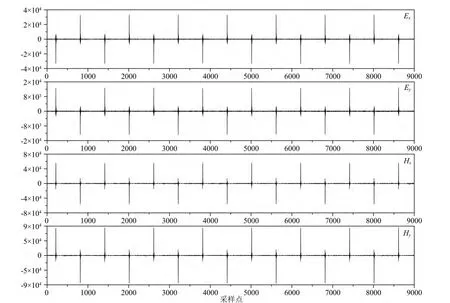
图5 测点ASY0002B受人工源干扰时间段经五点抛物线型结构元素形态滤波后的时间域波形（采样率为150Hz）Fig.5 Mathematical morphology with 5points parabola processing result of time series segments including controlled－source noise with a sampling rate of 150Hz at site ASY0002B

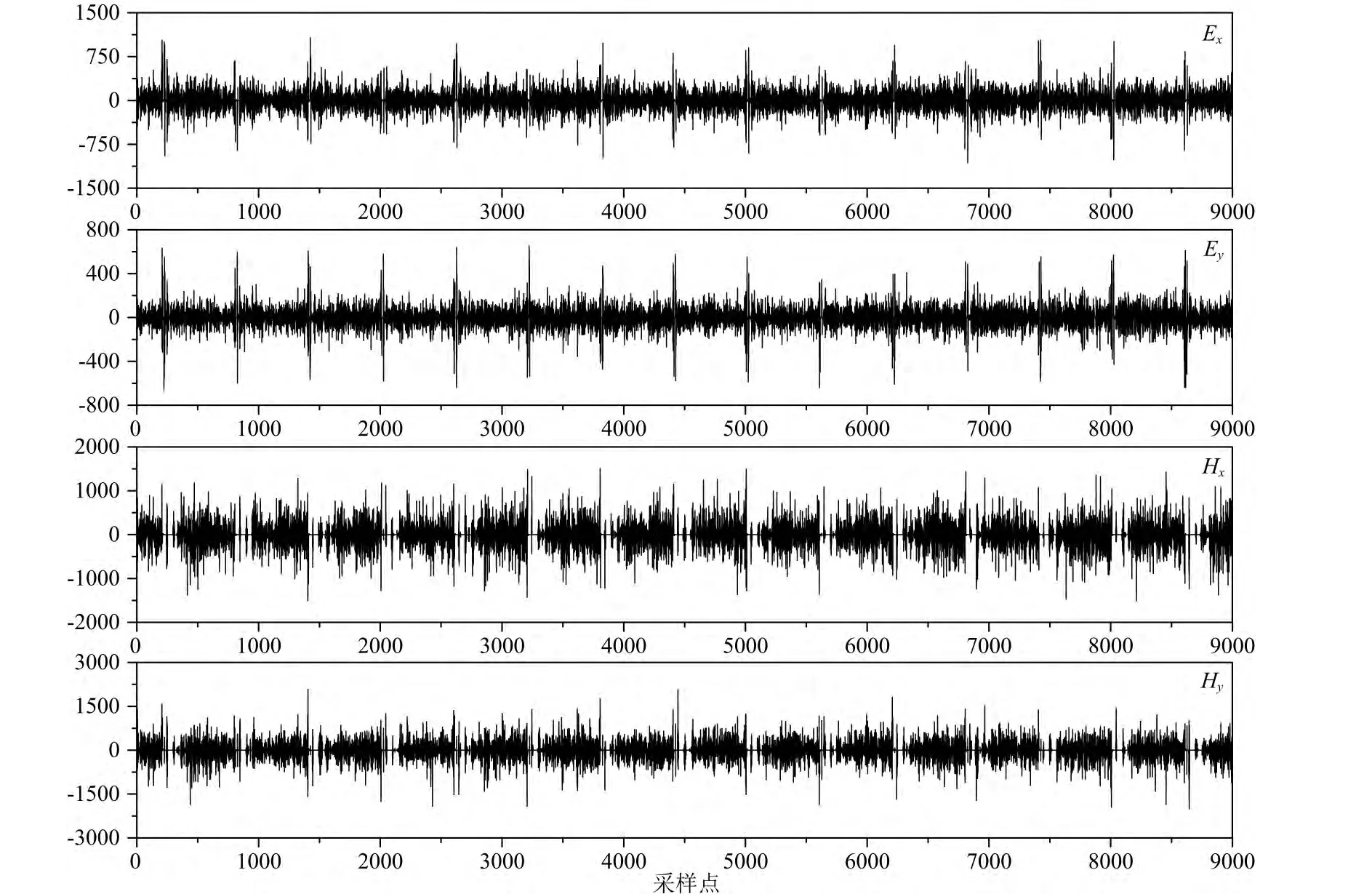
图6 测点ASY0002B受人工源干扰时间段形态滤波和阈值处理后的时间域波形（采样率为150Hz，形态滤波取3点抛物线，阈值取全时段算术平均值）Fig.6 Mathematical morphology and threshold processing result of time series segments including controlled－source noise with a sampling rate of 150Hz at site ASY0002B（The structural element of mathematical morphology is 3 points parabola，the threshold is arithmetic mean value of all time）

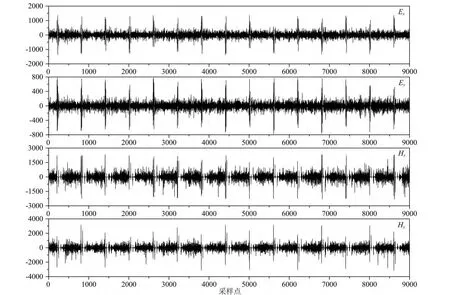
图7 测点ASY0002B受人工源干扰时间段形态滤波和阈值处理后的时间域波形（采样率为150Hz，形态滤波取3点抛物线，阈值取干扰时段算术平均值）Fig.7 Mathematical morphology and threshold processing result of time series segments including controlled－source noise with a sampling rate of 150Hz at site ASY0002B（The structural element of mathematical morphology is 3 points parabola，the threshold is arithmetic mean value of time with controlled－source noise）

经过上述处理分析可知，对于AMT数据而言，运用数学形态滤波进行强干扰压制是合理的、有效的；在结构元素的选择方面要根据干扰的类型和尺度进行试验，选取合适的结构元素；在阈值的选取方面要根据干扰信号的强度、干扰信号所占的比例等各项条件进行综合考虑.此次针对受到强干扰的原始时间域信号在经过数学形态滤波和阈值处理之后，有效地去除了其中存在的大尺度的干扰噪声，从中提取出了稳定的天然场信号，提高了数据的信噪比，这就为后续的阻抗估计和视电阻率－相位的计算提供一个可靠的保障.

3.3 处理效果评价

在本文中作者利用视电阻率－相位曲线、频谱以及极化方向等多个参数对处理效果进行了分析评价.

3.3.1 视电阻率－相位曲线

图8a为处理之后的视电阻率－相位曲线，对比图3可以看出，处理后的曲线在没有经过功率谱挑选的情况下，相对于图3a来说已经基本消除了其存在的问题，中低频数据质量得到了明显的提高，曲线比较光滑、连续，近源效应也得到了有效压制，处理后的曲线与无干扰时间段的曲线相比十分接近；图9给出了处理前后的视电阻率－相位相对误差曲线，对处理结果进行定量分析，由图可以看出在高中频（除“死频带”数据之外）二者相对误差基本上小于10%，而低频数据中个别频点由于受到的干扰比较严重，相对误差较大，说明此次的处理效果明显，大幅提高了数据质量.此外，在XY方向1000Hz左右存在的脱节现象，经过简单的功率谱挑选之后可以得到恢复.这也说明通过形态滤波和阈值处理，有效地去除了人工源强干扰，恢复了原有的曲线形态，可以提供真实的地下介质构造信息.

3.3.2 频谱

频谱分析是一种有效地判别噪声干扰的方法.傅里叶变换是最基本的时频分析方法，但它存在一定的局限性，即不能同时提供时频信息；而小波变换能将交织在一起的不同频率组成的混合信号分解成不同频率的信号块，通过伸缩和平移运算对信号进行多尺度分析，具有较高的分辨率，因而能有效地应用于信噪分离（范翠松等，2008；汤井田和何继善，2005）.本文即采用小波变换对信号进行频谱分析.图10为测点TS4文件（采样率150Hz）未受干扰时间段、受干扰时间段以及处理之后的Ex、Hy的频谱对比结果，由图可以看出在未受干扰时间段，频谱光滑，无毛刺，符合天然场的基本特性；在受到干扰时间段的频谱其幅值有了明显的增大，在舒曼谐振等频点存在的局部极值被干扰信号淹没，高频段更加光滑，特别是在中低频其受干扰的程度更加明显，其频谱出现多个极值，跳变严重；在经过处理之后，有效地降低了频谱的幅值，其舒曼谐振等局部极值也有所呈现，由于干扰所导致的严重跳变在经过处理之后也得到了明显的压制，频谱幅值更加合理；但二者之间仍存在一定差异，这是由于处理之后的时间域信号仍保留了一些小尺度的干扰，其中50Hz处出现的极大值可能是由于引入了人工虚假噪声导致的，但对整体效果影响不大.

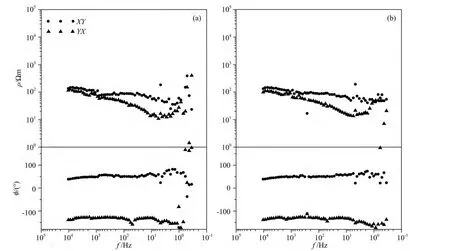
图8 测点ASY0002B视电阻率－相位曲线（a）处理后；（b）无人工源干扰时间段.Fig.8 Apparent resistivity and phase curves at site ASY0002B（a）After processing；（b）Calculated by data segment without controlled－source noise.

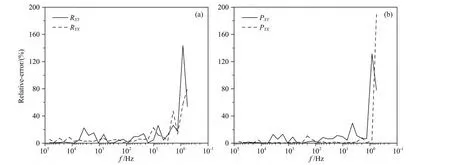
图9 测点ASY0002B处理前后视电阻率（a）、相位（b）相对误差曲线Fig.9 The relative error curves of apparent resistivity（a）and phase（b）at site ASY0002Bbefore and after processing

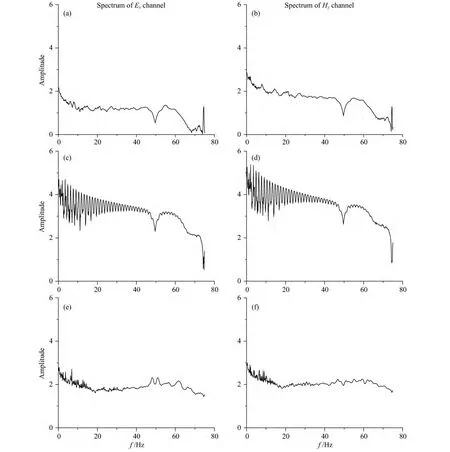
图10 处理前后频谱对比图（a、b）未受人工源干扰时间段的频谱；（c、d）受人工源干扰时间段频谱；（e、f）受人工源干扰时间段处理后的频谱.Fig.10 The comparison chart of spectrum in before and after processing（a，b）With no controlled－source noise；（c，d）With controlled－source noise；（e，f）After processing.

3.3.2 极化方向

电磁场极化方向也是评价电磁场受干扰程度的一个重要指标（Weckmann U.et al.，2005；张弛，2013），由于天然场由不同的源激励生成，因此其电磁场的极化方向也是随机的，随着时间的变化表现出无规律性，无序性；而受到噪声干扰时，其极化方向角度应比较集中.图11是处理前后电磁场的极化方向图，由图11（a、b）可知：在未受到干扰的时间段内，电磁场的极化角度是随机的、无序的，符合天然场极化方向的基本特征；而在干扰时间段内其极化角度比较集中，可以近似为一条直线，电磁场极化角度在8Hz时主要集中在－35°和－80°左右，同时也说明在该时间段存在一个比较稳定的人工源干扰.图11（c、d）是经过处理之后的结果，可以看出此时在受干扰时间段电磁场的极化角度相对于处理之前得到了明显的改善，角度比较随机无序，这也说明在一定程度上去除了噪声干扰，提高了数据质量.

针对本文所述处理方法进行梳理，给出了处理流程图，如图12所示.对于受到人工源干扰的数据，首先根据时间域数据的特征对其进行合理的时间段挑选，利用数学形态滤波对受干扰的时间域数据进行处理；然后以全时段的算术平均值为阈值进一步去除经过数学形态滤波后保留的幅值较大的脉冲干扰；最后是将处理后的时间域数据和无干扰时间域数据进行拼接，得到全时段数据以进行后续的阻抗估计和视电阻率计算.

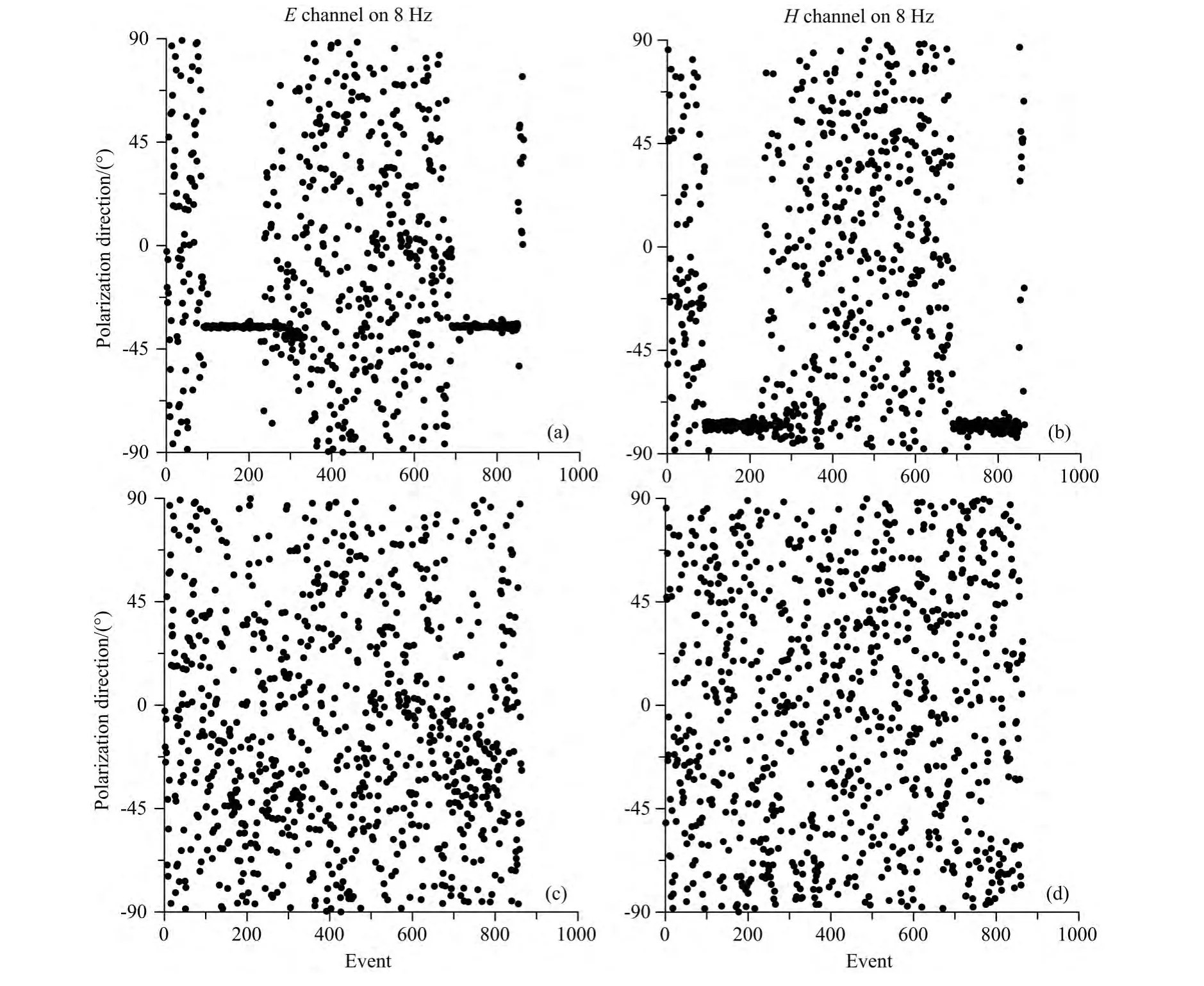
图11 测点处理前后8Hz时电磁场极化方向对比图（a、b）处理前；（c、d）处理后.Fig.11 The comparison chart of polarization direction at 8Hz（a，b）Before processing；（c，d）After processing.

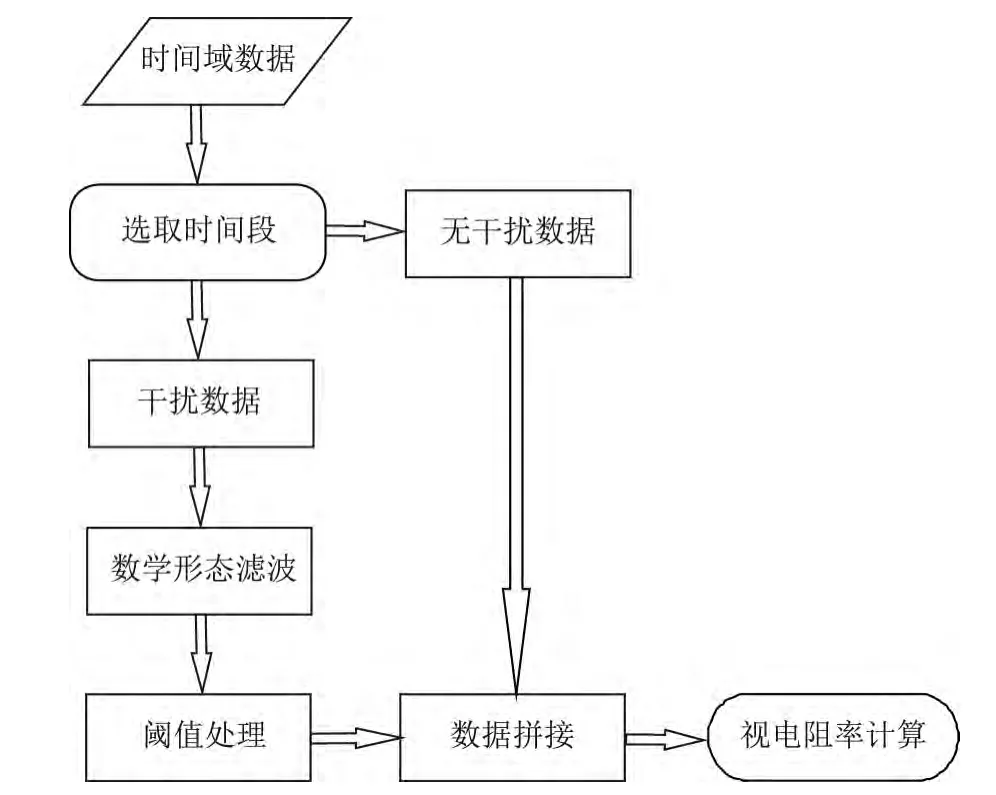
图12 数据处理流程图Fig.12 The flow chart of the data processing

综上所述，数学形态滤波可以有效地压制时间域信号中存在的人工源强干扰噪声，阈值法可以去除经过形态滤波处理之后保留的脉冲信号，可以有效地恢复天然场信号，提高信噪比.通过对视电阻率－相位曲线、频谱以及极化方向的对比分析也验证了方法的有效性.

4 结论

本文针对AMT信号中存在的强干扰噪声，通过时间域数学形态滤波与阈值法相结合的手段对数据进行去噪处理，取得了较好的效果.得出以下几点结论.

（1）在本次试验中，人工源强干扰噪声主要影响AMT的中低频数据（200Hz以下），导致视电阻率在200Hz处出现脱节；XY方向3Hz以下呈近源效应，YX 方向在200Hz以下跳变严重，基本无形态；高频数据由于位于源的远区受干扰程度较小，可以不做处理.

（2）在结构元素合理的前提下，数学形态滤波可以实现对强干扰噪声识别和去除；阈值法可以有效地压制脉冲干扰，二者相互结合处理可以实现对相关强干扰噪声的有效压制.其视电阻率－相位曲线、频谱和极化方向等参数都有明显的改善；

（3）数学形态滤波运用到AMT数据的强干扰压制中是有效的、合理的，可以运用到矿集区AMT数据的强干扰压制中；在结构元素的选取上要根据干扰类型和尺度等多方面因素进行综合考虑，进而选取合适的结构元素；同时如何实现结构元素类型和尺寸的自适应选取，是有待进一步解决的关键问题.致谢感谢所有参与野外数据采集的人员及张弛在本文撰写过程中给予的宝贵意见和建议；感谢审稿人提出的建设性意见.

Egbert G D，Booker J R.1986.Robust estimation of geomagnetic transfer functions.Geophysical Journal of the Royal Astronomical Society，87（1）：173－194.

Fan C S，Li T L，Wang D Y.2008.Treatment of watelet transform for square wave noise in MT data.Journal of Jilin University（Earth Science Edition）（in Chinese），38（Suppl.）：61－63.

Fan C S.2009.The strong noises characteristics of MT in ore concentration area and research of denoise method（in Chinese）［Ph.M.thesis］.Changchun：Jilin University.

Gamble T D，Goubau W M，Clarke J.1979.Magnetotellurics with a remote magnetic reference.Geophysics，44（1）：53－68.

Garcia X，Jones A G.2005.A new methodology for the acquisition and processing of audio－magnetotelluric （AMT）data in the AMT dead band.Geophysics，70（5）：G119－G126.

Goubau W M，Gamble T D，Clarke J.1978.Magnetotelluric data analysis：Removal of bias.Geophysics，43（6）：1157－1166.

Kaufman A A，Keller G V.1987.The Magnetotelluric Sounding Method（in Chinese）.Liu G D Trans.Beijing：Seismological Press.

Li J.2012.Magnetotelluric strong interference separation and application based on mathematical morphology （in Chinese）［Ph.D.thesis］.Changsha：Central South University.

Li J M.2005.Geoelectric Field and Electrical exploration（in Chinese）.Beijing：Geological Publishing House.

Tang J T，He J S.2005.Controlled Source Audio Magnetotelluric Method and Its Application（in Chinese）.Changsha：Central South University Press.

Tang J T，Li J，Xiao X，et al.2012a.Magnetotelluric sounding data strong interference separation method based on mathematical morphology filtering.Journal of Central South University（Science and Technology）（in Chinese），43（6）：2215－2221.

Tang J T，Li J，Xiao X，et al.2012b.Mathematical morphology filtering an noise suppression of magnetotelluric sounding data.Chinese J.Geophys.（in Chinese），55（5）：1784－1793，doi：10.6038／j.issn.0001－5733.2012.05.036.

Tang J T，Xu Z M，Xiao X，et al.2012c.Effect rules of strong noise on Magnetotelluric（MT）sounding in the Luzong ore cluster area.Chinese J.Geophys.（in Chinese），55（12）：4147－4159，doi：10.6038／j.issn.0001－5733.2012.12.027.

Tang L，Tang H Z，Han X P，et al.2013.The application of mathematical morphological filtering to the noise suppression of Audio Magnetotelluric Sounding data.Chinese Journal of Engineering Geophysics （in Chinese），10（4）：533－538.

Weckmann U，Magunia A，Ritter O.2005.Effective noise separation for magnetotelluric single site data processing using a frequency domain selection scheme.Geophysical Journal International，161（3）：635－652.

Wei W B.2002.New advance and prospect of magnetotelluric sounding（MT）in China.Progress in Geophysics（in Chinese），17（2）：245－254，doi：10.3969／j.issn.1004－2903.2002.02.009.

Zhang C.2013.Research on some techniques for magnetotelluric data processing（in Chinese）［Master thesis］.Changsha：Central South University.

附中文参考文献

范翠松，李桐林，王大勇.2008.小波变换对MT数据中方波噪声的处理.吉林大学学报（地球科学版），38（增刊）：61－63.

范翠松.2009.矿集区强干扰大地电磁噪声特点及去噪方法研究［硕士论文］.长春：吉林大学.

考夫曼，凯勒.1987.大地电磁测深法.刘国栋译.北京：地震出版社.

李晋.2012.基于数学形态学的大地电磁强干扰分离及应用［博士论文］.长沙：中南大学.

李金铭.2005.地电场与电法勘探.北京：地质出版社.

汤井田，何继善.2005.可控源音频大地电磁法及其应用.长沙：中南大学出版社.

汤井田，李晋，肖晓等.2012a.基于数学形态滤波的大地电磁强干扰分离方法.中南大学学报（自然科学版），43（6）：2215－2221.

汤井田，李晋，肖晓等.2012b.数学形态滤波与大地电磁噪声压制.地球物理学报，55（5）：1784－1793，doi：10.6038／j.issn.0001－5733.2012.05.036.

汤井田，徐志敏，肖晓等.2012c.庐枞矿集区大地电磁测深强噪声的影响规律.地球物理学报，55（12）：4147－4159，doi：10.6038／j.issn.0001－5733.2012.12.027.

汤磊，汤洪志，韩雪平等.2013.数学形态滤波在音频大地电磁去噪中的应用.工程地球物理学报，10（4）：533－538.