基于非线性规划全局优化问题的两种优化算法
2015-05-12王萍
王 萍
(铁岭师范高等专科学校,辽宁 铁岭 112000)
基于非线性规划全局优化问题的两种优化算法
王 萍
(铁岭师范高等专科学校,辽宁 铁岭 112000)
提出针对全局优化问题的非线性规划的随机算法进行探讨,给出适用于全局优化问题中的带有非线性约束的两种算法——模拟退火算法和进化规划算法。算法通过构造子问题来寻找优于当前局部最优解的可行解。该子问题可通过给出的两种随机算法——模拟退火算法和进化规划算法求解。求解子问题后,当前最优解被不断地更新,最终求得全局最优解。本算法应用于几个典型例题,并与基于模拟退火的罚函数法相比较,数值结果表明该算法是可行的、有效的。
非线性规划;模拟退火算法;进化规划算法
0 引言
模拟退火思想最早在1953年时由Metropolis[1]提出,之后Kirkpatrick和Aart等分别于1983年[2]和1987年提出将模拟退火算法应用于组合优化问题和模拟退火算法的理论和应用。王卓鹏等[3]研究出一种快速模拟退火算法,用来加快模拟退火算法的速度:先对样本点进行局部搜索之后再随机搜索。在关于退火策略研究方面,部分专家提出了对数下降、快速下降、直线下降和指数退温策略[4],例如顾基发、杨若黎,给出了与迭代次数有关的退火策略,同时给出一个退火准则[5]。
Fogel在20世纪60年代提出进化规划。他给出的方法和遗传算法有不少共同之处,但又不同于遗传算法,他强调父代与子代的表现行为联系上[6]。Fogel在1966年编著了《基于模拟进化的人工智能》,详细叙述了进化规划思想。到了90年代,学术界开始对进化规划加以重视。
1 目标函数是线性的非线性规划问题
本文给出了带有线性目标函数的非线性规划问题的模拟退火和进化规划算法,该方法将带有约束问题转变为无约束,数值结果证实方法计算精度高,显示了很好的收敛效果,考虑如下优化问题(其中c是向量):
mincTx
s.t.gi(x)≤0i=1,…,r
(1)
Ax≤b
为了寻找到满足约束的可行解,我们首先来解决子问题:
minf=max{0,gi(x)i=1,…,r}
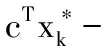
(2)
Ax≤b
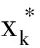
Bx≤d可写成:
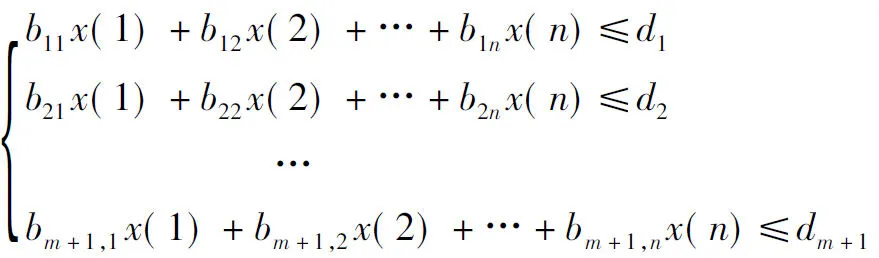
(3)
2 非线性规划全局优化问题的模拟退火算法
基于分量x(li)的上下界我们提出了一类求解子问题(3)的模拟退火算法,算法的具体步骤如下:
算法1:Step 0:初始化:给定最高和最低温度分别为Tmax,Tmin,迭代次数Lmax以及参数ε>0。
Step1:利用随机过程,得到可行解的初始值x0=(x0(1),…,x0(n)),设T=Tmax,t=0,I=0。若f(x0)≤0,则I=1,y*=x0。否则转step2。
Step2: While (T>Tmin) do
(a) whilet≤Lmaxdo
(1)随机地选取lt∈{1,2,…,n},给出均匀分布的随机数λ∈[-1,1]。Forj=1,…,n,ifλ>0,
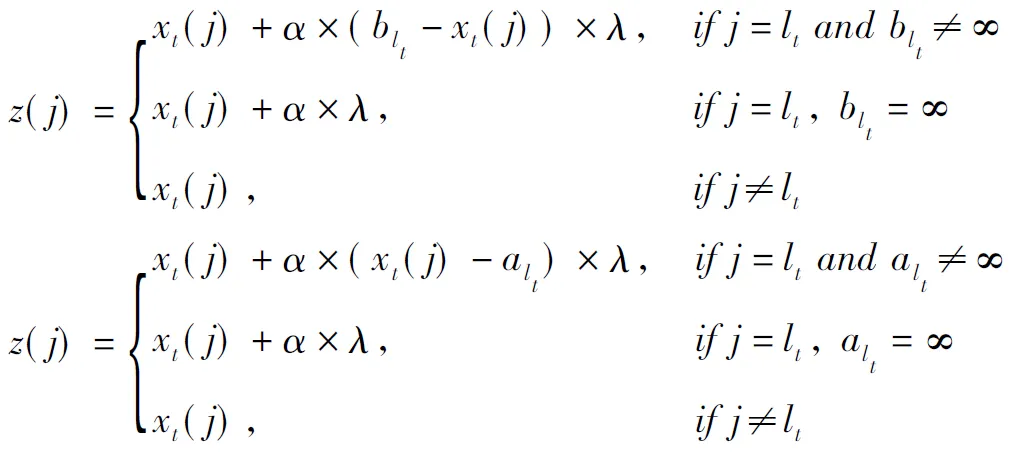
其中alt和blt为下界和上界xt(lt)来自于不等式(3),α的初值为1,若α<10-4,则α=1。
(2)令z=(z(1),…,z(n)),如果f(z)≤0,则I=1,y*=z。算法1则停。否则转(3)。
(3)取η∈[0,1],如果η≤min{1,exp{[f(xt)-f(z)]/T}},设xt+1=z,否则xt+1=xt。t=t+1。
(b)Lmax=Lmax+d,t=0.
(c)由T=δ×T降低温度T。其中,参数d,β和δ为事先输入的已知常数。
在算法1的基础上,给出随机的可行解初始值x0,令k=0。如果I=1,令xk+1*=y*,Tmax=T,Lmax=Lmax,k=k+1。如果I=0,则xk*就是问题(1)的全局最优解。
3 非线性规划全局优化问题的进化规划算法
本节针对问题(2)给出一个改进的进化规划算法,适应值即取目标函数值,具体步骤如下:
算法2:Step1:给出μ个初始值,设k=1,I=0。设个体为实值向量对(xi,ηi),∀i∈{1,…,μ}。
Step2:计算个体适应值。如果∃i∈{i,…,μ},f(xi)≤0,则I=1,y*=xi′否则转Step3。
Step3:每个父代(xi,ηi),∀i=1,…,μ,根据如下步骤产生一个子代(xi′,ηi′):从集合{1,2,…,n}中随机的选取li,产生介于[-1,1]区间的均匀分布随机参数λ。对于j=1,…,n,如果λ>0
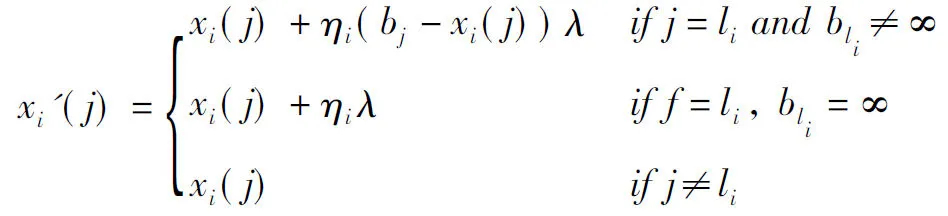
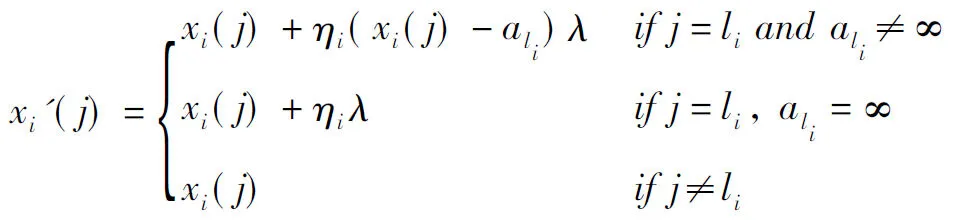
η的初始值为1,如果ηi<10-4,那么ηi=1。
Step4:若适应值≤0个数为0,令k=k+1,转Step3。若适应值≤0的个数>0,算法2则停。
基于算法2,我们提出求解问题(1)的算法,给出随机的μ个可行解初始值xi,∀i∈{1,…,μ},令t=1。如果I=1,令xi′*=y*,t=t+1。如果I=0,则xi*就是问题(1)的全局最优解。
4 数值结果
下面我们给出求解的数值例子:
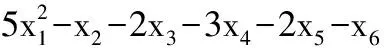
s.t.x1+2x2+8x3+x4+3x5+5x6≤16 and -8x1-4x2-2x3+2x4+4x5-x6≤-1,
2x1+0.5x2+0.2x3-3x4-x5-4x6≤24 and 0.2x1+2x2+0.1x3-4x4+2x5+2x6≤12,
-0.1x1-0.5x2+2x3+5x4-5x5+3x6≤3 andx4≤1,x5≤1 andx6≤2 andxi≥0,(i=1,…,6)
该函数的全局最优解为(0,6,0,1,1,0),最优值为-11。
表1示出了进行数值计算的参数设定值,表2和表3是数值计算结果。
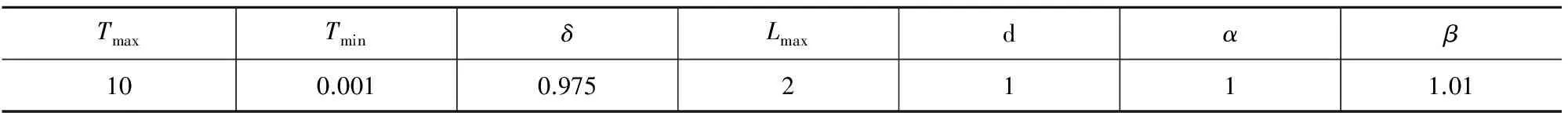
表1 模拟退火算法的参数设定值

表2 基于文中提出的模拟退火算法和罚函数法计算结果

表3 基于本文进化规划算法和罚函数法计算结果
[1]Metropolis N, Rosenbluth A. Rosenbluth M. et al.. Equation of State Calculations by Fast Computing Machines[J].Journal of Chemical Physics,1953,(21):1 087—1 092.
[2]Kirkpatrick S., Gelatt Jr C,D. and Vecchi M P.. Optimization by Simulated Annealing[J].Science,1983,(220):671—680.
[3]王卓鹏,高国成,杨卫平.一种改进的快速模拟退火组合优化法[J].系统工程理论与实践,1999,(2):73—76.
[4]高尚.模拟退火算法中的退火策略研究[J].航空计算技术,2002,32(4):20—23.
[5]杨若黎,顾其发.一种高效的退火全局优化算法[J].系统工程理论与实践,1997,(5):29—35.
[6]Heitkotter, J. and Beasley, D.. The hitch-hiker’s guide to evolutionary computation[J].FAQ in Comp Ai Genetic,1995.
责任编辑:柴造坡
10.3969/j.issn.1674-6341.2015.06.047
2015-09-11
王萍(1981—),女,辽宁铁岭人,硕士研究生,讲师。研究方向:数学教育与教学。
G642.4
A
1674-6341(2015)06-0101-02
