小调整 大提升

王立松

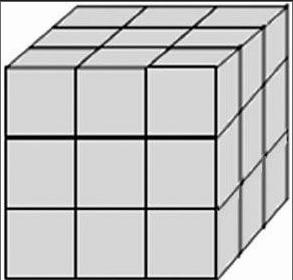
原题：下图是由27个小正方体拼成的一个大正方体，把它的表面积全部涂成绿色，请想一想：

（1）没有涂到颜色的小正方体有多少块？

（2）一面涂色的小正方体有多少块？

（3）两面涂色的小正方体有多少块？

（4）三面涂色的小正方体有多少块？

第一层次：尝试做。

目的在于让学生尝试自己独立完成。

【设计意图】实验版教材在“长方体和正方体的表面积”知识编排时有些不合理，它是按由难到易编排的。因此，学生完成这道题的结果大相径庭：对于问题（1），不少学生无法知晓结果，问题（2）、（3）、（4），学生解题正确率由少到多。

第二层次：小调整。

（1）三面涂到颜色的小正方体位于大正方体的什么位置？三面涂到颜色的小正方体的块数是多少？

（2）两面涂到颜色的小正方体位于大正方体的什么位置？两面涂到颜色的小正方体的块数是多少？

（3）一面涂到颜色的小正方体位于大正方体的什么位置？一面涂到颜色的小正方体的块数是多少？

（4）没有涂到颜色的小正方体位于大正方体的什么位置？没有涂到颜色的小正方体的块数是多少？

【设计意图】如此调整，遵循了解题的规律——由易到难。而这道题包含有“点线面体”的知识，考虑此题时不妨先求三面涂色的块数，再求两面和一面涂色的，最后求不涂色的。因为计算三面涂色的需借助正方体顶点的知识，不论怎样的正方体和长方体，如果表面涂色，三面涂色的一定是8个。而计算两面涂色的块数要借助正方体的棱的知识，计算一面涂色的借助面的知识，计算不涂色的块数则需借助里层的小正方形体。

第三层次：大提升。

根据上面的做法，如果把小方块的块数由27块改成64块和125块，三面涂色、两面涂色、一面涂色和没有涂色的各是多少块？再把这三种进行比较，你有什么发现？

【设计意图】通过研究27块小正方体组成一个大正方体，再调整到64块和125块小正方体组成的大正方体。这样，通过比较与分析，学生的思维得到了较大提升，会得出这样的规律：表面涂色的一个大正方体分割成几个小正方体后，三面涂色的一定是8个，两面涂色的有（n-2）×12，一面涂色的有（n-2）2×6，不涂色的有（n-2）3。（n为一条棱上的小正方体个数）明白了正方体的涂色规律，长方体的涂色规律的掌握也就易如反掌。

（作者单位：安徽省铜陵市金口岭小学 责任编辑：王彬）endprint