基于卡方拟合度的无线传感器网络数据复原汇聚方法

孔贵琴， 李 智

(四川大学 电子与信息学院，四川 成都 610041)

基于卡方拟合度的无线传感器网络数据复原汇聚方法

孔贵琴， 李 智

(四川大学 电子与信息学院，四川 成都 610041)

在无线传感器网络(WSNs)中，现有的数据复原汇聚算法不能准确判断节点感知数据的受攻击程度，数据复原精度偏低，故提出了一种基于卡方拟合度的分布式数据复原汇聚算法。该算法根据不同时刻节点感知数据的时间相关性特点来构造各节点信任权值计算当前时刻各簇数据样本的估计值，并利用卡方拟合度来衡量此时各个簇的受攻击程度，最后通过加权运算提高了算法的数据复原精度。另外，由于卡方拟合度能够准确感知数据的细微波动，该方法对网络噪声干扰的稳健性有很大提高。仿真结果表明:该算法的数据复原汇聚精度大幅度提高，优于现有数据复原汇聚算法。

无线传感器网络； 数据复原汇聚； 卡方拟合度； 时间相关性

0 引 言

在无线传感器网络(WSNs)中，数据汇聚是各种应用的基础，能有效减少冗余数据的传输，延长网络寿命。目前数据汇聚面临的一个难题是节点感知数据容易遭到恶意的篡改。这种攻击主要分为两类，一类是节点感知数据在传输过程中被修改，此种情况可以通过加密技术检测出来，另一类是节点感知数据在汇聚之前被篡改，这种攻击无法利用加密技术检测并阻止[1]。因此,数据汇聚算法主要用来解决这种问题，在感知数据输入到聚合函数之前对其进行检测。然而在检测到攻击时，传统的方法会直接丢弃此次采集的数据[2,3]，这种处理结果会导致大量的资源浪费，降低网络能量利用率。

针对此问题，Wagner David提出了几种简单的数据复原汇聚方法[4]，如截断法、剪切法等。在此工作基础上，数据汇聚复原方法得到很大的改进和提高。但是这些方法在实际中有很大的局限性。Buttyan L等人[1]提出了基于随机取样一致性检验法(RANSAC-based resilient aggregation，RANBRA)，该方法通过随机取样将模型与样本进行一致性检验，不断地剔除异常节点数据，重复实验后，将最终剩下的数据集合作为聚合函数的输入。但是这种方法采用的是集中式数据处理方式，节点能耗较高，而且当网络中不存在攻击时仍然有大量的数据被剔除掉，因此，汇聚精度较低。文献[5]提出一种基于灰色关联度和概率密度距离的数据复原汇聚方法[5](gray relationship degree and probability density parallel distance-based resilient data aggregation，GPDRDA)，该方法采用分布式汇聚的模型，用灰色关联度和概率密度距离共同衡量各簇节点的受攻击程度，并赋予权值，然后进行加权聚合运算，汇聚精度得到一定提升，但其抗噪声性能较差。基于此，文献[6]提出一种基于相似度的WSNs数据复原汇聚方法[6](similarity-based resilient data aggregation，SIMRDA)，该方法的复原汇聚精度较高，且对网络噪声干扰的稳健性较强，但是当敌方对俘获节点感知数据施加的攻击量较小时，此方法不能准确选取未受攻击或受攻击较弱的期望模型，致使汇聚复原精度得不到较大的提高。

本文提出一种基于卡方拟合度的WSNs数据复原算法(Chi-square goodness of fitting based resilient data aggregation,CSFRDA)。

1 数据复原汇聚模型

本文中采用分簇方式将网络均分成若干个簇，每个簇选出自己的簇头。簇内的节点将数据传给簇头，然后在簇头处进行汇聚，最后簇头将汇聚结果通过无线多跳路由传递给基站[7]。

基于实现，本文做如下假设：

2)受攻击节点比例k≤0.5:实际中由于攻击者能量有限，网络中受攻击的节点数量不会很大，本文中设最大的比例为0.5。如果攻击者攻击的范围覆盖了整个网络，那么，数据复原汇聚将失去意义。

3)受攻击节点集中于网络中的某些簇:现实中，攻击者往往是在其操作方便的范围内进行工作，因而，可合理假设受攻击的节点比较集中。

2 基于时间相关性与卡方拟合度的数据汇聚

根据数据复原汇聚模型，统一假设变量，n表示网络中节点总数；r表示分簇的数目；Ci表示第i个簇；m表示簇Ci所含节点数；Xij表示簇Ci中第j个节点的读数，假设网络中不存在攻击，则节点读数Xij服从独立同分布，且期望u未知，σ2已知；k表示受攻击节点比例。

本文中聚合函数f(·)为求均值，X为聚合函数要得到的目标变量，为X的估计量，i为簇Ci的目标变量Xi的估计值。distortion为估计值与真值之间的绝对偏差，有

distortion=|-X|.

(1)

2.1 时间相关性

Mehmet C Vuran 等人在WSNs领域明确提出了时间相关性和空间相关性的概念[8]，WSNs中传感器节点由于分布比较密集所采集到的数据具有一定的空间相关性，如果采样间隔足够小，相邻间隔之间的采样数据同时具有时间相关性。

首先利用节点存储的前t个时刻的历史数据来判断当前时刻感知数据的信任度。当攻击量较大时，采用卡方拟合检验法[9]选取一个未遭受攻击或受攻击最弱的簇作为期望模型Cz，通过比较Ci与Cz中数据的差异来判断Ci中数据的受攻击程度。

定义1Aij表示当前时刻网络受攻击后Ci中第j个节点的读数,Bij表示Ci中第j个节点的前N个时刻历史数据均值,则Ci中第j个节点的信任度为

(2)

其中

(3)

对每个节点的信任度归一化

(4)

则第i个簇的估计值

(5)

di=|i-z|.

(6)

2.2 卡方拟合度

当攻击量较小时采用卡方统计量[10]作为各个簇在汇聚时的测度。

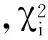
(7)

定义4 第i个簇中节点感知数据的卡方拟合度为

(8)

2.3 基于卡方拟合度的数据复原算法的基本原理

当敌方对俘获节点感知数据所施加的攻击量较大时，受攻击的簇内节点数据与未受攻击的簇内节点数据差异较为明显，因此,可选取期望簇Cz，利用各个簇与期望簇之间的重心距离来反映簇中节点数据受攻击的程度，如式(6)。

此时簇Ci数据复原汇聚权值wi，wi为Ci重心距离所对应的权值。

将wi与另外r-1个非期望簇的估计值进行如下加权运算

(9)

将由式(9)求得的值与期望模型的估计值再进行一次聚合，得到最终的聚合结果

(10)

但是当攻击量较小时，网络中节点的感知数据波动不大 ，此时,利用SIMRDA方法无法准确选取网络中未受攻击或受攻击最弱的簇为期望模型，导致汇聚复原的结果不准确(第三部分会给予证明)。因此,本文中为避免选取期望模型造成的误差，采用卡方拟合度直接判断攻击量较小时各个簇受攻击的程度。

由式(7)可知，卡方值反映了实际频数与理论频数的吻合程度，如果假设样本服从理论分布成立，则实际频数和理论频数之差一般不会很大;反之，实际频数和理论频数之差会很大。由此可知，χi越小，实际样本与理论样本越接近。

此时簇Ci数据复原汇聚权值vi,vi为Ci卡方拟合度对应的权值。

将各簇的估计值与对应的权值进行加权运算得到最终的聚合结果

(11)

式(9)和式(11)中wi和vi可根据拉格朗日极值法求得[7]

(12)

(13)

3 计算机仿真与分析

将1000个传感器节点随机部署在100 m×100 m的区域内，并将它们均匀划分10个簇，每个簇包含100个传感器节点。假设当网络中不存在攻击时，节点感知数据服从N(0,σ2)，显著性水平α=0.05。攻击方式为常量攻击，聚合函数f(·)为求均值，传感器节点可存储前100个时刻的感知数据。针对不同的k值，每次试验重复进行50次。仿真图中横坐标表示受攻击节点所占比例，纵坐标表示真值与聚合结果之间的绝对偏差。

3.1 CSFRDA与RANBRA的性能比较

图1是CSFRDA与RANBRA的性能比较，横轴表示受攻击节点比例k取不同的值，纵轴表示对每个k值汇聚算法得到的结果与真实值之间的绝对偏差。此时σ2=5,d=10，CSFRDA采用重心距离做测度。从图中可以看出，CSFRDA的性能要好于RANBRA,这是由于CSFRDA合理利用了所有节点的感知数据，而RANBRA通过样本数据与随机抽取的期望模型进行一致性检验，丢弃了一些异常数据，造成信息量的损失。另外，CSFRDA中的的分簇方法使得受攻击节点集中于某些簇内，并且受攻击节点越集中，汇聚复原误差越小。

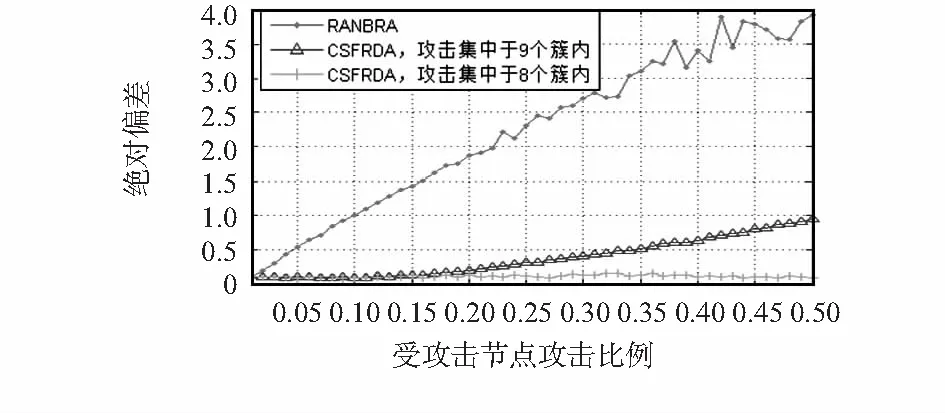
图1 CSFRDA与RANBRA的性能比较

3.2 CSFRDA和GPDRDA与SIMRDA的比较

3.2.1 复原汇聚性能比较

图2和图3分别表示当攻击量较小时，SIMRDA和CSFRDA各个簇在汇聚时所占的权重w(攻击集中在第1～8簇中)。

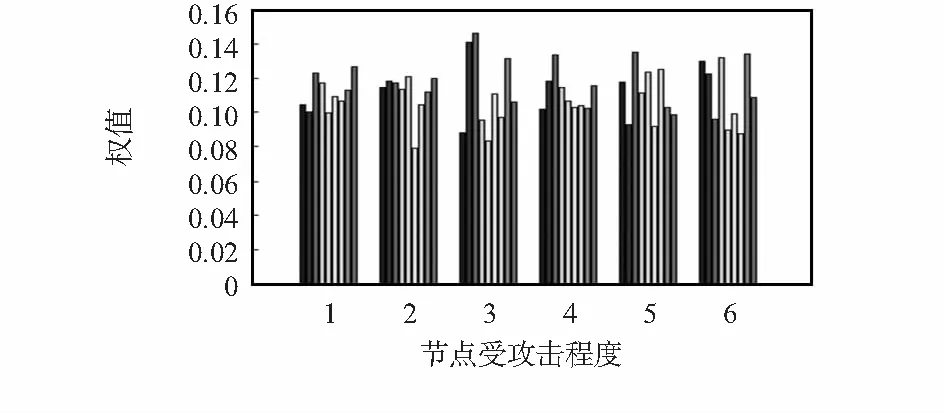
图2 SIMRDA中d=0.5时各个簇汇聚时的权值

图3 CSFRDA中d=0.5时各个簇汇聚时的权值

图2中，SIMRDA方法中选出第10个簇为期望簇，攻击集中在第1～8簇中，由图可以看出:在SIMRDA方法中,当节点受攻击程度不同时，各个簇与期望簇的相似度差异无明显区别，汇聚权值均保持在0.1～0.12，该方法无法准确判断出各个簇的受攻击程度；而图3中，CSFRDA方法不用选出期望簇，未受攻击的第9,10两个簇和受攻击的8个簇之间的权值相差很大，随着攻击节点比例k越大，这个特点越明显。这表明:CSFRDA方法可以明显判断出网络中各簇的受攻击程度，并准确地赋予其汇聚权值。

图4和图5分别表示攻击增量为0.5和10时CSFRDA,GPDRDA和SIMRDA的复原汇聚效果对比。从这两幅图中可以看出：CSFRDA的性能优于GPDRDA和SIMRDA。

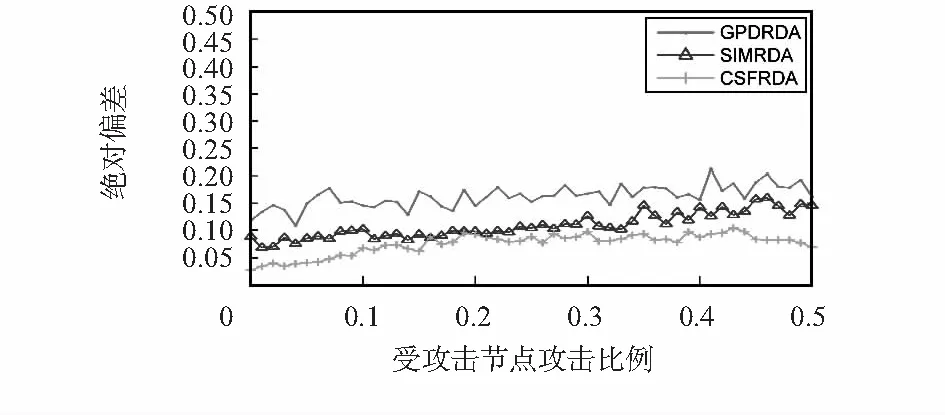
图4 d=0.5时三种方法的性能比较

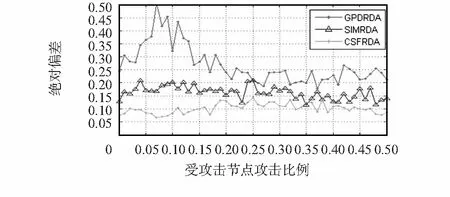
图5 d=10时三种方法的性能比较

由图4可知,当d=0.5时，SIMRDA采用相关系数作为汇聚加权系数，但是从图2中可以看出:相关系数并不能很好地表示各个簇的权重；GPDRDA采用灰色关联度做测度，同样需要选出期望簇，而当节点数据波动较小时选择期望模型会产生很大的误差。图3表明:CSFRDA利用卡方拟合度可以准确地表示各个簇在数据汇聚时所占的权重。从图4中可以看出：GPDRDA数据复原误差区间为0.1～0.2；SIMRDA保持在0.075～0.15；而CSFRDA数据复原误差为0.05～0.1,较前两种方法分别降低了50 %和33.33 %。

由图5可知，当d=10时， GPDRDA和SIMRDA采用均值表示簇的目标变量的估计值，而CSFRDA在汇聚时用到的各簇目标变量的估计值是利用节点数据时间相关性融合簇内数据得到的，精确度较高，故最终利用各个簇与期望模型之间的差异来复原的误差也较小。从图5中可以看出，GPDRDA数据复原误差开始在0.25～0.5波动，最后保持在0.2～0.25；SIMRDA的误差为0.15～0.2，最后保持在0.15不变；而CSFRDA的数据复原误差开始在0.075～0.125波动，最后保持在0.1不变,较前两种方法分别降低了63.75 %和38.54 %。

3.2.2 抗噪声性能比较

图6 SNR=-5 dB时三种方法的抗噪声性能比较

图7 SNR=0 dB时三种方法的抗噪声性能比较

从图6和图7中可以看出：当信噪比为-5,0dB时，CSFRDA的抗噪声性能约是SIMRDA的2倍、GPDRDA的3倍(k≤0.3)，当k>0.3以后随着k取值增大，CSFRDA的抗噪性能减弱，但仍优于GPDRDA和SIMRDA。这是因为在攻击量较小时，各个簇的数据之间的差异不大，无法正确的选出期望簇，而CSFRDA利用卡方拟合度可以准确地表示各个簇在汇聚中所占的权重，避免了GPDRDA和SIMRDA中由于选期望模型造成的误差，所以,CSFRDA对噪声干扰的稳健性更强。

4 结束语

基于现有的复原汇聚算法精度较低和对网络噪声干扰的稳健性较差等方面的不足，本文提出了一种基于卡方拟合度的WSNs数据复原方法，利用卡方拟合度和重心距离分别表示在攻击者施加的攻击量不同时各个簇的受攻击程度，提高了数据复原汇聚的精度，且增强了对网络噪声干扰的稳健性。理论分析和仿真结果表明:本文中提出的方法整体性能优于现有的复原汇聚方法。

[1]ButtyanL,SchafferP,VajdaI.RANBAR:RANSAC-basedresi-lientaggregationinsensornetworks[C]∥ProceedingsofthefourthACMWorkshoponSecurityofAdHocandSensorNetworks:ACM,2006:83-90.

[2]RenShuqin,ParkJS.Densityminingbasedresilientdataaggregationforwirelesssensornetworks[C]∥FourthInternationalConferenceon2008NetworkedComputingandAdvancedInformationManagement,NCM’08,IEEE,2008,1:261-266.

[3] Buttyan L,Schaffer P,Vajjda I.Resilient aggregation with attack detection in sensor networks[C]∥2006 Fourth Annual IEEE International Conference on Pervasive Computing and Communications Workshops 2006,PerCom Workshops, IEEE,2006:336.

[4] Wagfer D.Resilient aggregation in sensor networks[C]∥Proc of the 2nd ACM Workshop on Security of Ad Hoc and Sensor Networks:ACM,2004:78-87.

[5] 罗永健,丁小勇,罗相根,等.一种有效的无线传感器网络数据复原汇聚方法[J].数据采集与处理,2011(1):90-94.

[6] 罗永健,史德阳,侯银涛,等.基于相似度的无线传感器网络数据复原汇聚方法[J].计算机应用研究,2012(9):3405-3407.

[7] 杨 军,张德运,张云翼,等.基于分簇的无线传感器网络数据汇聚传送协议[J].软件学报,2010(5):1127-1137.

[8] Vuran M C,Akan Ö B,AkyildizI F.Spatio-temporal correlation:Theory and applications for wireless sensor networks[J].Compu-ter Networks,2004,45(3):245-259.

[9] 杨 鑫.无线传感器网络中的数据复原汇聚方法 [D].西安:西安通信学院,2008.

[10] 亓民勇,董金新.基于卡方拟合优度检验的序列等概性测试组[J].计算机工程与设计,2012(5):1757-1760.

Resilient data aggregation method for WSNs based on

Chi-square goodness of fitting KONG Gui-qin, LI Zhi

(College of Electronics and Information Engineering,Sichuan University,Chengdu 610041,China)

The existing resilient data aggregation algorithm doesn’t accurately judge under-attack level of each node in wireless sensor networks(WSNs),resulting in a low precision,propose a distributed resilient data aggregation algorithm based on Chi-square goodness of fitting.The algorithm firstly construct weights of trust of each node,calculates current estimation value of data sample of each cluster by exploiting time correlation of a sensor node at different time,to evaluate attack level using Chi-square goodness of fitting.Finally,through weighted arithmetic,increase precision of data recovery.In addition,Chi-square goodness of fitting can sense to slight data fluctuations,accurately thus the presented algorithm can better improve robust of network noise.Simulation result shows that data aggregation precision of the presented algorithm is greatly improved,which is better than existing data resilient aggregation algorithm.

wireless sensor networks(WSNs); data resilient aggregation; Chi-square goodness of fitting; time correlation

2014—08—01

10.13873/J.1000—9787(2015)04—0130—04

TP 274

A

1000—9787(2015)04—0130—04

孔贵琴(1988-)，女，湖北黄冈人，硕士研究生，主要研究方向为无线传感器网络技术。