基于无线传感器网络的自适应声源定位算法*
2015-05-11申晓红闫永胜王海燕
张 秀, 申晓红, 闫永胜, 王海燕
(西北工业大学 航海学院,陕西 西安 710072)
基于无线传感器网络的自适应声源定位算法*
张 秀, 申晓红, 闫永胜, 王海燕
(西北工业大学 航海学院,陕西 西安 710072)
基于声源能量的无线传感器网络(WSNs)最大似然定位算法抗噪声干扰能力强,定位精度高,同时适用于多个目标定位,但是计算量大,不适用于实时定位。针对现有算法的缺点,提出了一种基于自适应迭代的最大似然定位算法。该算法将代价函数作为目标函数,在给定的梯度误差范围内自适应地搜索目标位置。为了提高算法的收敛速度和定位精度,提出了基于Sigmoid函数的变步长的搜索算法。仿真实验结果表明:与最大似然定位算法相比,自适应迭代算法运算量小,定位精度高,能满足对目标定位精度和速度要求较高的场合,具有一定的实际应用意义。
无线传感器网络; 最大似然定位; 声源能量; 自适应; 时变步长; 高精度
0 引 言
基于声源信号的无线传感器网络具有普适性、隐蔽性和鲁棒性的特点,传感器网络根据声源信号进行目标定位的方法主要有三种:基于信号时延的测量方法TDOA[2](time delay of arrival),基于目标信号角度的测量方法DOA[3](direction of arrival)及基于目标信号强度指标的测量方法RSSI[4](received signal strength indication)。TDOA方法主要是通过信号到达两个传感器节点之间的时间差求出距离差,根据距离差实现对目标的有效定位,对节点之间时间同步精度有非常高的要求;DOA方法主要依靠在传感器节点上安装天线阵列来获得角度信息,再通过三角测量法计算出节点的位置,对节点硬件要求较高,需要大量的计算和通信开销。RSSI通过接收到的信号强弱对两个通信节点间的距离进行估算,进而根据相应的数据进行定位,定位原理简单,且无需额外的硬件开销和网络通信开销,易于工程实现,比较适合于无线传感器网络。
目前,RSSI方法主要有:CPA[6]、最大似然法[5~7]、能量比例法[8]。CPA算法简单易于实现,但只应用于单目标定位且定位精度较低;能量比例法与CPA一样,仅适用于单目标定位,其算法一般采用非线性最小二乘法或线性最小二乘法求解,定位速度快,但受噪声的影响较大;最大似然法[3]抗噪声干扰能力强,精度高,是RSSI算法中精度最高的一种方法,同时适用于多个目标定位,但由于该算法要对节点布置区域进行搜索,所以,其运算量较大,实时性较差,不利于在线对目标进行跟踪。
针对最大似然法存在的缺点,本文提出了一种基于自适应迭代的最大似然(AML)定位算法,该算法将代价函数作为目标函数,在给定的梯度误差范围内自适应地搜索目标位置。为了提高算法的收敛速度和定位精度,采用基于Sigmoid函数的时变步长进行搜索,可以通过选择不同的误差范围和迭代次数均衡计算量与定位精度,实验结果表明:该算法具有更高的定位精度和更广的适用范围。
1 最大似然定位法
在目标定位问题中,声音能量变化问题可以看作是点声源的能量变化问题。点状声源发出的声波在均匀介质中的声强与距离的平方呈反比,如球面扩展的水声信号能量衰减模型。因此,假设目标源是点状声源,以球面扩展均匀地向四周辐射声音能量,则传感器节点接收到的能量与传感器距目标之间的距离平方呈反比。由此,假设在一个由N个传感器节点组成的无线传感器网络中,测到某未知目标所发射的信号能量,则第i个传感器接收到的能量为
(1)
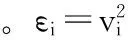
在已知能量衰落模型的基础上,可以应用最大似然估计[9,10]的方法来求解此模型。为求解简便,首先由式(1)可以得到
方案一PPS含基布滤料 (纤维长度51 mm)5块:样品1~5,方案二PPS无基布滤料A(纤维长度51 mm)5块:样品6~10,方案三PPS无基布滤料B(纤维长度76 mm)5块:样品11~15。
(2)
式(2)用矩阵形式可表示为
Z=GDS+ζ.
(3)
其中,H=GD,S=[S1S2…SN]T,
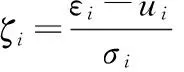
(4)
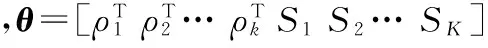
l(θ)=‖Z-GDS‖2,
(5)
达到最小值时的θ值。
最大似然定位法就是在传感器布放的区域内搜索使得L最大的θ值,则对应的θ值即为目标位置。
2 基于自适应迭代的最大似然定位算法
2.1 算法描述
由式(6)可以得到关于位置参数的梯度
(6)
具体的迭代步骤如下:
1)在搜索范围内,给出迭代初始点ρ0,终止误差ε>0,给定最大迭代次数maxiter。


2.2 时变步长的选取
在一般情况下,当用最速下降法寻找极小值点时,其搜索路径呈直角锯齿状;其次,在收敛的初始阶段,目标函数下降较快,但在接近极小点时,收敛速度就不理想了,如图1所示。为了克服这两点,本文研究了时变步长的迭代,即在初始收敛阶段或未知系统参数发生变化时,步长应比较大,以便有较快的收敛速度和对时变系统的跟踪速度;当目标函数收敛后,无论干扰信号有多大,均应保持很小的调整步长以达到很小的稳态失调噪声。本文给出了Sigmoid函数变步长算法[11]
(7)
其中,参数α 控制函数的形状,β控制函数的取值范围。根据自适应滤波算法[12]的收敛条件:0
为了进一步研究参数α,β对时变步长的影响,绘制在不同参数下步长u(k)和代价函数l(k)的关系曲线。由图3、图4可知,当l(k)较大时,u(k)也较大,但u(k)不会超出界限β/2。α选择过大时代价函数l(k)在接近0时仍有较大步长,稳态误差增大,α选择过小时步长较小且变化缓慢,收敛速度降低;β选择过大时会超出收敛条件,过小时初始阶段收敛速度较慢。通过大量仿真得到,βmax=20/S时为最佳值,即以初始步长为收敛步长的10倍开始搜索,随着代价函数的减小,步长自适应地减小,直到函数收敛;通过大量仿真得到,α的最佳值的取值范围为α∈(0,100),且α的最佳值的取值与传感器个数呈正比,传感器数量越多,α的最佳值取值越大;反之,则越小。
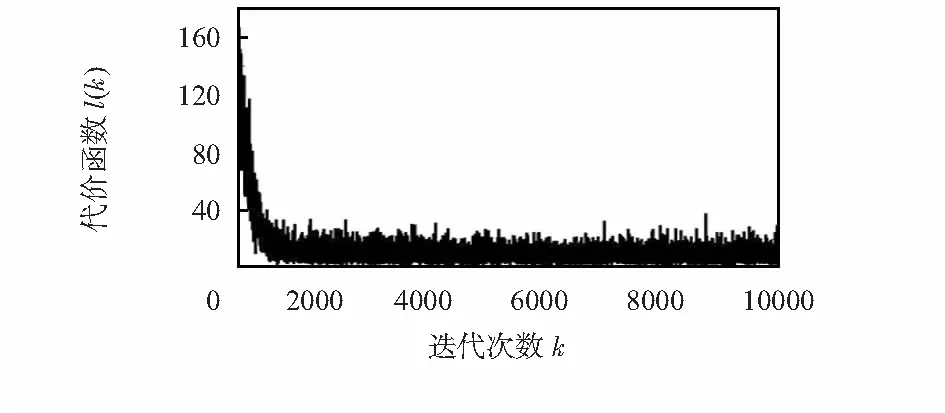
图1 固定步长的学习曲线

图2 时变步长的学习曲线
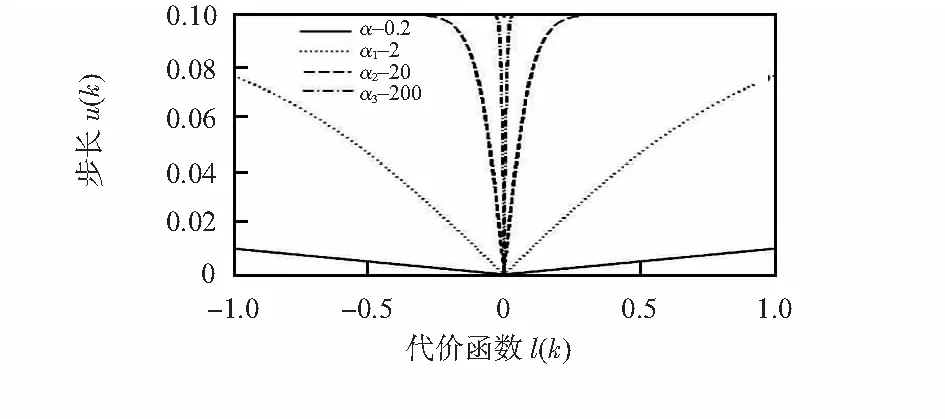
图3 α不同且β=0.2时的关系曲线
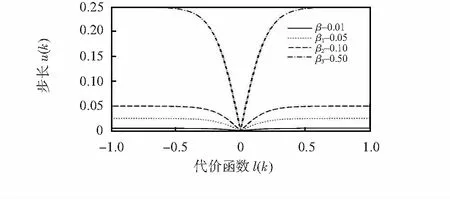
图4 α=10且β不同时的关系曲线
3 仿真实验结果

在仿真实验中,对四种目标定位方法(CPA,LS,ML,AML)的结果都进行Ns=1 000次独立仿真,每次仿真得到一个定位估计,返回一个估计误差值,然后求得误差值的均值和协方差。
表1为四种定位算法在不同传感器节点数目下的误差和协方差。从表1可以看出:随着传感器数目的增加,各算法的误差均值相应地减少。文中提出的AML算法在三种传感器节点数目不同的情况下,其误差均值都比另外三种算法小,可以达到很好的定位精度,在性能上是持续稳定的。另外,从协方差矩阵中可以看出:误差值的横纵坐标之间是不相关的。
图5为四种定位算法距离误差定位分布。将得到的关于估计位置与实际位置的距离差,以5m为一个单位递增,用柱状图表示出来。从图5的误差分布图可以看出,AML算法的误差稳定地集中在低误差范围内,证明了其在定位过程中能持续稳定地进行高精度定位,验证了其可靠性和有效性。
最大似然定位的搜索算法的运算量的复杂度为O(L2×N×Ns),基于自适应迭代算法的运算量的复杂度为O(N×iter×Ns),iter为自适应迭代时达到给定误差后自动停下来时已经迭代的次数。表2为在本文仿真条件下,两种算法的运算量的复杂度。
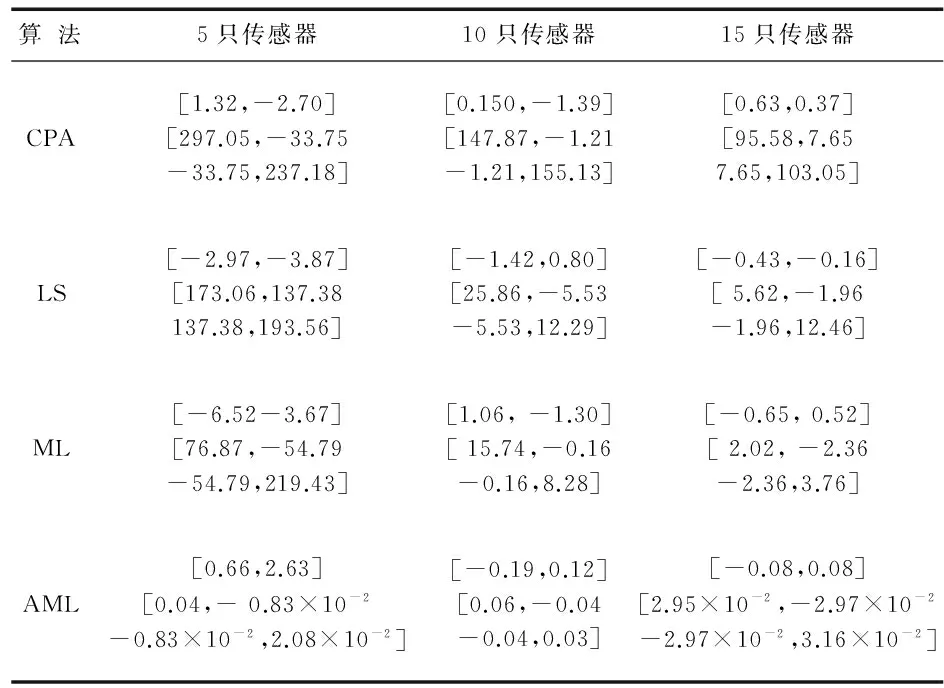
表1 四种算法的误差均值和协方差
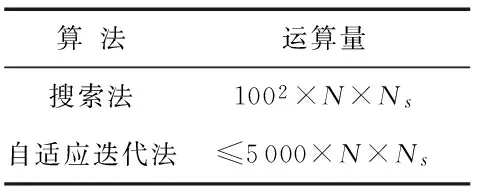
表2 最大似然法的运算量复杂度比较
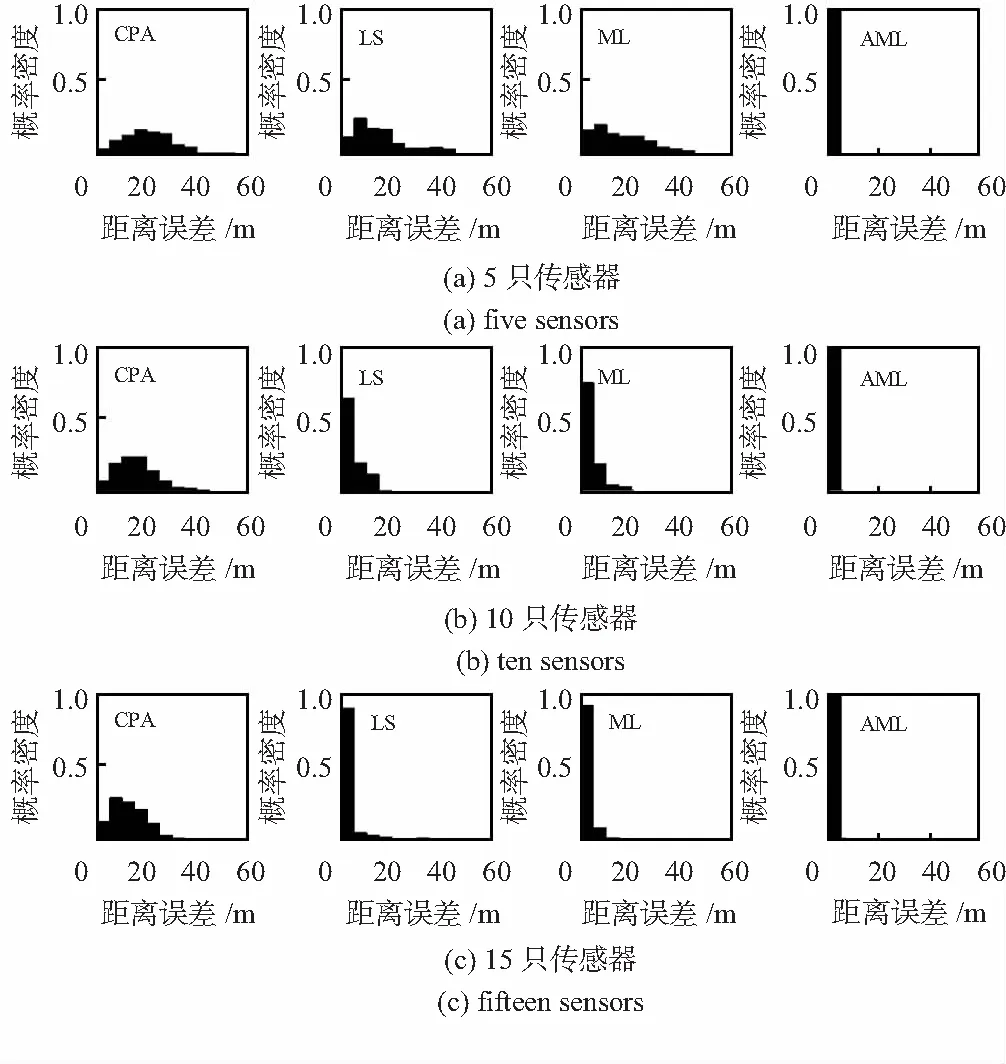
图5 四种算法的误差估计分布
4 结 论
本文提出的算法和最大似然法相较于其他两种算法(CPA算法、LS算法),定位误差明显要小,而且可以定位多个目标(今后进一步研究),而与最大似然法相比,定位误差更小,运算复杂度也更小,而且在传感器节点数目设置不同时,其表现出了定位精度的持续稳定性,不易受参数扰动的影响。因此,本文算法能满足对目标定位精度和速度要求较高的场合,具有一定的实际应用意义。
[1] 孙利民.无线传感器网络[M].北京:清华大学出版社,2005:3-25.
[2] Gillette M D,Silverman H F.A linear closed-form algorithm for source localization from time-differences of arrival[J].Signal Processing Letters,IEEE,2008,15:1-4.
[3] 张子涵.基于水下传感器网络的目标定位研究[D].镇江:江苏科技大学,2012:17-30.
[4] Wang B,Li Y,Huang H,et al.Target localization in underwater acoustic sensor networks[C]∥Congress on Image and Signal Processing,CISP’08,IEEE,2008:68-72.
[5] Ma Y,Hu Y H.ML source localization theory in an underwater wireless sensor array network[C]∥5th International Conference on Wireless Communications,Networking and Mobile Computing,WiCom’09,IEEE,2009:1-4.
[6] 刘立阳,张金成,吴中林,等.基于RSSI&DFP的无线传感器网络声源目标定位算法[J].传感技术学报,2011,24(10):1464-1468.
[7] 戎 舟.WSNs基于声音能量量化数据的目标定位研究[J].计算机应用研究,2012,29(11):4312-4314.
[8] Yan Yongsheng,Wang Haiyan,Wang Xuan.A novel least-square method of source localization based on acoustic energy measurements for UWSN[C]∥2011 IEEE International Conference on Signal Processing,Communications and Computing(ICSPCC),IEEE,2011:1-5.
[9] Haykin S S.Adaptive filter theory[M].Noida,India:Pearson Education India,2005.
[10] 魏雅川,梁 彦,陈延军,等.无线传感器网络自适应声音目标定位算法[J].传感技术学报,2010,23(3):418-422.
[11] 高 鹰,谢胜利.一种变步长LMS自适应滤波算法及分析[J].电子学报,2001,29(8):1094-1097.
[12] So H C,Ching P C.Comparative study of five LMS-based adaptive time delay estimators[J].IEE Proceedings of Radar,Sonar and Navigation,2001,148(1):9-15.
张 秀 (1990-), 女,陕西榆林人,硕士研究生,主要从事信号与信息处理、无线传感器网络的研究。
Adaptive acoustic source localization algorithm based on
wireless sensor networks*ZHANG Xiu, SHEN Xiao-hong, YAN Yong-sheng, WANG Hai-yan
(School of Marine Science and Technology,Northwestern Polytechnical University, Xi’an 710072,China)
The maximum likelihood(ML)localization algorithm for wireless sensor networks(WSNs)based on acoustic source energy has strong anti-noise ability,high precision,and it is suitable for multiple targets localization at the same time;but it needs large amount of calculation and is not suitable for real-time positioning.Aiming at shortcoming of the existing algorithm,propose a maximum likelihood localization algorithm based on adaptive iteration.The new algorithm treats the cost function as objective function and search target location adaptively in given range of gradient error.Propose variable step size searching algorithm,based on Sigmoid function,in order to improve convergence speed and positioning precision.Simulation experiment result show that compared with the maximum likelihood localization algorithm,the proposed algorithm has less amount of calculation,high positioning precision, so it can meet the requirement of higher positioning precision and speed,has certain practical significance.
wireless sensor networks(WSNs); the maximum likelihood positioning; acoustic source energy; adaptive; time variable step size; high precision
2014—08—28
国家科技重大专项项目(2011ZX05026—001—06)
10.13873/J.1000—9787(2015)04—0115—04
TP 393
A
1000—9787(2015)04—0115—04
