基于边缘定向的图像插值算法*

李 跃，许少秋

（广东工业大学信息工程学院，广东广州 510006）

0 引言

随着数字图像处理技术的发展，图像超分辨率重建应用领域及其宽广，在军事、医学、公共安全和计算机视觉等方面都存在着重要的应用前景。图像超分辨率算法可分为多帧超分辨率算法和单帧超分辨率算法，由于基于多帧的超分辨率算法不仅利用了单帧图像的信息，还利用不同图像之间类似又不完全相同的性质，比单帧的超分辨率算法处理效果更好。例如基于非局部POCS的超分辨率图像重建[1]，利用一帧图片中的重复的局部结构块得到冗余信息从而锐化边缘，得到质量较高的图像。还有利用多帧图像序列的相似性进行矩阵填充和矩阵恢复获得高分辨率图像[2]，也能得到不错的效果。但在很多现实情况下，由于存在各种条件的限制，无法在同一个场景获得多帧图像，所以基于单帧的超分辨率研究是非常有必要的，也越来越受到重视。

本文是研究基于插值提高单帧图像分辨率的算法。由于传统插值算法没有考虑边缘的特性，图像经过处理后在边缘处存在模糊的现象，影响图像的质量。一些基于边缘的插值算法例如ICBI[3]虽然也考虑了边缘的特性，但是存在计算量大，无法进行任意倍数放大等缺陷。本文提出一种基于边缘定向的插值算法。通过计算图像非平坦区边缘的主导方向，在该区待插值位置沿着主导方向进行线性插值。而对于平坦区域则直接采用线性插值。该方法计算简单，插值不受边缘方向的限制，并可进行任意倍数的图像放大。本文结构安排如下：第二部分介绍传统插值算法；第三部分介绍拉普拉斯滤波增强；第四部分介绍基于边缘定向的插值算法；第五部分是实验结果与分析；最后是结论。

1 传统线性插值算法

图像插值是图像处理的重要内容之一，就是利用邻近像素点的灰度值得到待插点的灰度值，从而使一幅低分辨率的图像经过处理得到分辨率更高的图像。

传统双线性插值算法，对于一个目的像素，设置坐标通过反向变换得到的浮点坐标为(i+u，j+v)，其中 i、j均为非负整数，u、v为 [0，1]区间的浮点数，如图1所示，像素值f(i+u，j+v)可由原图像中(i，j)、(i+1，j)、(i，j+1)、(i+1，j+1)的像素值决定，即：

其中 f（i，j） 表示源图像 （i，j） 处的像素值。

图1 待插像素与周围像素

（双线性内插法）只考虑待插值点周围四个直接邻点的影响，具有低通滤波器的性质，导致图像的高频分量受损，并且只在水平和垂直方向上插值，没有考虑边缘的方向性，使插值后图像的边缘变得模糊（如图2所示）。

图2 荷花用Bilinear放大四倍的效果图

2 拉普拉斯预处理

由于插值算法通常是根据周围像素得到目标像素，对图像有一定的平滑作用，会使图像的细节丢失，所以在插值之前先用拉普拉斯滤波，增强图像的细节，缓解插值带来的平滑效果。拉普拉斯滤波结果g(x，y)定义如下：

式（2）-（4）中f（x，y）为图像像素值。

3 基于边缘定向的插值算法

本文提出一种基于边缘定向的线性插值算法，只需计算非平坦区域的主导边缘方向，在待插值位置沿该边缘方向进行插值就可以得到未知像素。

如图1所示，4个像素点(x，y)、 (x，y+1)、(x+1，y)、(x+1，y+1)构成一个插值区域。利用图3模板分别计算像素点水平和垂直方向的梯度分量Gx、Gy。

如果插值区域中像素点梯度分量|Gx|或|Gy|高于某个阈值，则该区域设为非平坦区，否则为平坦区。通常阈值可设置为0。平坦区可直接利用公式（1）进行插值。

图3 梯度计算模板

由于图像边缘方向所在直线与梯度方向所在直线互相垂直，定义边缘方向为它所在直线与水平轴正方向的逆时针夹角，取值范围为[0，π]。在非平坦区域中，区域的边缘主导方向θd可定义为：

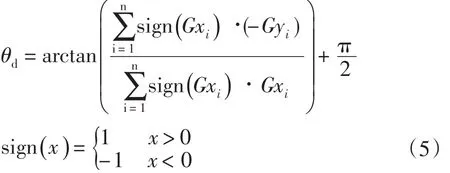
其中，n为区域像素点个数。

如图4所示，在非平坦区待插值位置沿边缘主导方向进行插值，存在6种可能的情况。图5给出其中一种情况的详细表示。如图5所示，通过待插值点画一条平行于区域边缘主导方向的直线，分别交区域边缘ab和ad于e和f两点。e点像素值可由a、b两点通过线性插值获得，同样地，f点像素值可由a、d两点通过线性插值获得。最后待插值点o的像素值可依据e、f两点通过线性插值获得。图4中其他情况插值操作类似。

基于边缘定向插值算法首先判断待插点所在区域是否处于平坦区，如果是则直接利用线性插值，如果不是则确定区域边缘的主导方向，在待插值位置沿该方向进行线性插值。

图4 边缘定向插值可能存在的情况

图5 插值例子

4 实验结果与分析

为了客观地评估本文算法，采用Berkeley分割图像库（http://www.eecs.berkeley.edu）以及GPR[4]中的图片，在MATLAB环境下比较其他算法（包括Bilinear，ICBI[3]和GPR[4]）与本文算法在视觉上以及数值上（采用评估指标SSIM[5]和PSNR)的不同。

如图6-9所示，从视觉效果来说，Bilinear算法图片细节比较模糊，在保持边缘平滑方面没有其他算法好，GPR算法细节清晰，但其运行结果容易出现一些原图没有的人造细节，ICBI边缘平滑效果比Bilinear好，细节模糊方面有所改善，但效果没本文算法好。从数值上来看，由于SSIM和PSNR值越高表示算法越优越，从图6和8可以看出本文算法性能良好，运行时间也较低。

图6 clock用4种算法放大2倍的效果图

图7 图6中选择区域的细节放大图

图8 蝴蝶用4种算法放大4倍的效果图

图9 图8中选择区域的细节放大图

表1和表2分别列出Barkeley分割图像库图片放大两倍和四倍的平均SSIM、PSNR和运行时间值。可以看出，不管用什么算法进行插值，放大倍数越大，SSIM和PSNR的值越小，失真越严重。GPR算法虽然效果较好，但运行时间最长。

表1 放大2倍下的数据平均值

表2 放大4倍下的数据平均值

5 结论

本文提出了一种基于边缘定向的插值算法来实现单帧图像超分辨率。在非平坦区待插值位置沿着区域边缘的主导方向进行线性插值。在平坦区域直接采用线性插值。该方法计算简单，可进行任意倍数的图像放大，结果显示该算法相对Bi⁃linear、GPR和ICBI具有一定的优越性。

［1］龚昌来，罗聪，杨冬涛，等.一种基于边缘方向的双线性插值方法［J］.激光与红外，2010，40（7）：788-791.

［2］张煜东，吴乐南.单帧图像的超分辨率技术进展［J］.光学技术，2008，34（增刊）：43-45，48.

［3］ Andrea Giachetti，Nicola Asuni.Fast artifacts-free im⁃age interpolation［A］.Proceedings of the British Ma⁃chine Vision Conference 2008［C］.2008：123-132.

［4］He He，Wan-Chi Siu.Single image super-resolution us⁃ing Gaussian process regression［A］.Computer Vision and Pattern Recognition ［C］.IEEE Conference on 2011：449-456.

［5］ Zhou Wang，Bovik，Sheikh，Simoncelli.Image quality assessment：from error visibility to structural similarity［J］.Image Processing，IEEE Transactions on，2004，13（4）：600-612.

［6］ Wing-Shan Tam，Chi-Wah Kok，Wan-Chi Siu.Modi⁃fied edge-directed interpolation for images［J］.Journal of Electronic Imaging， 2010， 19 （1） ：013011.1-013011.20.

［7］ Schultz R.R.，Stevenson R.L.A Bayesian approach to image expansion for improved definition［J］.Image Pro⁃cessing，IEEE Transactions on，1994，3（3）：233-242.

［8］C.Robert Appledorn.A new approach to the interpolation of sample data。［J］.Medical Imaging，IEEE Transac⁃tions on，1996，15（3）：369-376.

［9］ Luming Liang.Image interpolation by blending kernels［J］.Signal Processing Letters， IEEE， 2008， 15：805-808.

［10］罗国中，殷建平，祝恩，等.基于非局部POCS的超分辨率图像重建［J］.计算机科学，2014，41（8）：47-49，62.

［11］周春霞，吴锡生.基于方差和边缘插值的邻近点图像修复算法［J］.计算机工程与应用，2008，44（14）：184-186.

［12］王卓峥，贾克斌，刘帷.基于稀疏表示与矩阵填充的多帧超分辨率重建［J］.北京工业大学学报，2014，40（1）：38-42，48.