干燥带对接触网复合绝缘子电场分布的影响
2015-05-10张友鹏陈志东赵珊鹏
张友鹏, 陈志东, 赵珊鹏
(兰州交通大学 自动化与电气工程学院, 甘肃兰州 730070)
在接触网中,复合绝缘子用于将带有不同电位的导体在机械上相互连接且相互绝缘。接触网绝缘子安装高度低易受到尘埃、雾、雨、雪以及工业污染等不利因素的侵袭[1]。当绝缘子表面污层湿润后,污层电导率增大,绝缘子表面泄露电流迅速增大,闪络电压大大降低,绝缘子在工作电压下发生闪络[2]。由于绝缘子几何形状不同,污层电阻不均匀,因此绝缘子表面泄漏电流也不同,电流大的区域发热较多,将形成一条或多条干燥带[3]。
当干燥带出现时,干燥带处绝缘子沿面电场发生较大的畸变,一旦电场强度大于空气的击穿强度值时,将在绝缘子表面产生局部电弧,进而可能导致完全闪络。绝缘子闪络的根本原因是其表面电场发生畸变[4-7],因此,研究绝缘子表面出现干燥带后的电场强度分布情况可以为绝缘子的设计及闪络机理的研究提供参考。目前国内外一些学者主要采用矩形、锥形等几何形状简单的模型进行干燥带的影响分析[8-10],不能够很好地反映出绝缘子复杂几何形状可能带来的影响,有一些学者选用悬式瓷绝缘子作为研究对象[11],而对于柱式复合绝缘子的研究较少,由于接触网复合绝缘子有其特有的材质和结构,因此干燥带对其的影响规律并非与上述研究相同。
本文根据接触网复合绝缘子真实的几何结构,应用有限元软件COMSOL Multiphysics建立了染污接触网棒形柱式复合绝缘子二维仿真模型,选择软件中的电准静态场模块[12]分析绝缘子表面易形成干燥带的位置及干燥带的宽度、数目对电场分布的影响。
1 计算模型的建立
1.1 参数的确定
本文采用电气化铁路接触网FQBG-25/12型棒形柱式复合绝缘子,其结构高度880 mm,爬电距离1600 mm,大伞裙和小伞裙半径分别为188 mm和158 mm,大小伞裙个数分别为7个和6个。为了便于说明,文中将从绝缘子低压端起的第1、2、3,…,13个伞裙分别编号为1、2、3,…,13号伞裙。绝缘子高压端金具上电位为接触网最高网压交流峰值41 kV,低压端金具电位为0 V,电介质材料参数见表1。

表1 电介质材料参数
1.2 模型的建立
本文研究绝缘子表面出现干燥带最严重的情况,干燥带规则均匀绕径向一周[11],同时由于接触网绝缘子较电力系统绝缘子安装高度低,易受到列车经过时路面扬起的沙尘等因素的污染,文献[3]中设置污层厚度为0.15 mm,因此本文将污层厚度设为0.2 mm,且均匀的沉积在绝缘子表面。同时从工程近似的角度对模型进行了简化处理,将高压端、低压端金具用规则的圆柱体代替,忽略杆塔和导线对电场分布的影响,将整个模型视为轴对称[13-15]。应用有限元法软件COMSOL Multiphysics建立基于1/2轴截面的二维有限元模型,在不影响计算结果的前提下大大减少了计算量和计算时间。但由于有限元法只能解决有限域问题,因此本文采用人工截断法截取绝缘子周围空气为一定半径长度的圆域。通过计算得出当空气域半径分别取为2倍、5倍、8倍的绝缘子结构高度时,绝缘子表面最大电场强度分别为5.79、6.10、6.10 kV/cm,因此空气域半径选取为结构高度的5倍。

2 仿真结果及分析
2.1 清洁绝缘子电场分布
通过有限元计算,得到清洁状态下绝缘子沿面电场分布,见图3。绝缘子沿面电场强度整体呈“U”形分布,高压端和低压端附近电场强度相对较大。每个伞裙上电场强度分布情况相似,高压端处第一个伞裙(13号伞裙)和低压端处第一个伞裙(1号伞裙)的电场强度较其他伞裙电场强度大,因此在后续的研究中,选取13号伞裙作为分析对象说明干燥带对其伞裙上电场强度的影响。

2.2 干燥带最容易产生区域的分析
由于干燥带主要是由湿污层中绝缘子表面泄露电流发热生成,因此分析绝缘子表面湿污层中电流密度的大小可得出不同位置处形成干燥带的难易程度。本文通过在整个绝缘子表面沉积0.2 mm均匀厚度的湿污层,来分析工作电压下绝缘子沿面污层中各个位置的电流密度情况,见图4。

由图4可知, 绝缘子不同位置泄漏电流不同,但绝缘子每个伞裙及伞裙间柱体上泄漏电流有一定的相似性。伞裙间柱体表面泄漏电流较伞裙上下表面高,且泄露电流最低处为每个伞裙的边沿,因此绝缘子最容易出现干燥带的位置为伞裙间的柱体处,其次为伞裙的上下表面和伞裙边沿。
2.3 干燥带宽度的影响
干燥带处电场强度发生明显畸变,见图5,随着泄露电流加热的作用干燥带逐渐变宽,绝缘子伞裙上下表面以及伞裙间柱体上不同宽度的干燥带沿面电场分布见图6~图8。

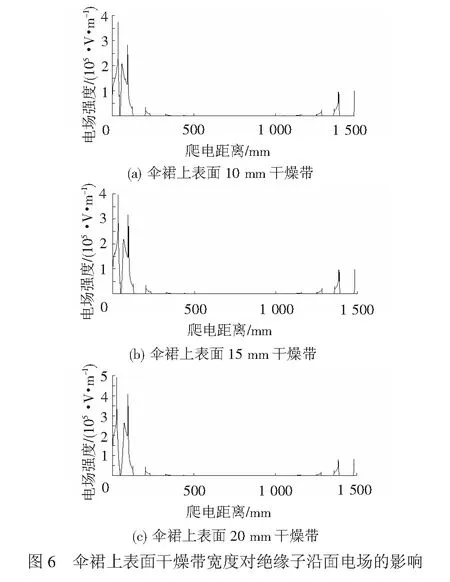


由图6可知,当伞裙上下表面产生干燥带且干燥带的宽度分别10、15、20 mm时,干燥带处最大电场强度分别为3.7、3.9、4.8 kV/cm。所以伞裙上表面干燥带处电场强度最大值随着干燥带宽度的增加而增大。伞裙下表面干燥带宽度为10、15、20 mm处,电场强度的最大值分别为3.1、3.6、4.1 kV/cm,电场强度最大值增加规律与伞裙上表面一致,见图7。由于伞群间柱体长度较短,因此本文选取柱体上干燥带宽度分别为5、10、15 mm进行分析。由图8可知,当柱体上干燥带宽度分别为5、10、15 mm时,最大场强分别为8.6、8.3、7.2 kV/cm,且最大值均出现在干燥带的端部。柱体上干燥带处电场强度最大值随干燥带宽度的变化情况与伞裙上下表面相反,随着干燥带宽度增大,干燥带处电场强度减小。
2.4 干燥带数目的影响
实际情况中由于受到自然条件和泄漏电流共同影响,绝缘子表面可能同时存在多条干燥带。本文分别分析了同一伞裙上出现多条干燥带,以及整个绝缘子柱体上存在多条干燥带时,干燥带处电场强度最大值变化情况。

如图9所示,绝缘子伞裙表面干燥带数目分别为4、6、8 条时,干燥带处绝缘子沿面最大电场强度分别为7.3、12.5、17.5 kV/cm。随着伞裙表面干燥带数目的增多,其电场强度最大值变化比较明显且相应增大。当每个伞群间柱体上仅有一条干燥带出现,整个绝缘子柱体上分别产生4、6、8 条干燥带时,其对应的沿面最大电场强度值分别为8.7、8.1、7.8 kV/cm,见图10。这与文献[3]中所计算的与柱式复合绝缘子结构相似的瓷支柱绝缘子干燥带处电场强度变化趋势相同,见表2。因此,当整个绝缘子柱体上干燥带数目逐渐增多时,其沿面场强最大值逐渐减小。

表2 绝缘子柱体上干燥带数目对电场影响对比

柱式复合绝缘子瓷支柱绝缘子[3]干燥带数目电场强度/(kV·cm-1)干燥带数目电场强度/(MV·m-1)28.726.5548.135.3187.844.48
3 结论
(1) 接触网棒形柱式复合绝缘子伞裙间柱体处泄露电流最大,最易出现干燥带。
(2) 伞裙上下表面干燥带处的场强最大值,随着干燥带宽度的增大而增大,且最大值出现在靠近柱体侧干燥带端部,而伞裙间柱体上最大值随着干燥带宽度的增加而减小。
(3) 干燥带数目对场强最大值影响较为明显,随着伞裙上干燥带数目的增多,场强最大值显著增大,而柱体上干燥带数目的增多,场强最大值有所降低。
参考文献:
[1] 张仁豫.绝缘子污秽放电[M]. 北京:水利电力出版社,1994.
[2] 关志成. 绝缘子及输变电设备外绝缘[M]. 北京清华大学出版社,2006.
[3] 徐志钮,律方成,李和明. 干燥带对染污支柱绝缘子电场分布影响[J].高电压技术,2011,37(2):276-283.
XU Zhi-niu,LV Fang-cheng,LI He-ming. Influence of Dry Band on Electric Field Distribution of Polluted Post Insulator[J].HighVoltage Engineering,2011,37(2):276-283.
[4] 樊亚东,文习山,李晓萍.复合绝缘子和玻璃绝缘子电位分布数值仿真[J]. 高电压技术,2005,31(12):1-3.
FAN Ya-dong,WEN Xi-shan,LI Xiaoping.Numerical Simulation of Electric Potential Distribution of CompositeInsulator and Glass Insulator[J]. HighVoltage Engineering,2005,31(12):1-3.
[5] 谢天喜,刘鹏,李靖,等. 交流1000kV同塔双回输电线路复合绝缘子电场分布[J]. 高电压技术,2009,35(6):1279-1283.
XIE Tian-xi,LIU Peng,LI Jing,et al.Electric Field Distribution of Composite Insulator on AC 1000 kV Double Circuit Transmission Line on the Same Tower[J]. HighVoltage Engineering, 2009,35(6):1279-1283.
[6] 金涛,文闿成. 外绝缘表面有湿污电导时交流电场的计算研究[J]. 中国电力,1994,27(6):11-15.
JIN Tao,WEN Kai-cheng.Calculation of AC Electric Field at the Outer Insulating Surface Withwet Dirt Conductance[J]. Electric Power,1994, 27(6):11-15.
[7] 司马文霞,邵进,杨庆. 应用有限元法计算覆冰合成绝缘子电位分布[J]. 高电压技术,2007,33(4):21-25.
SIMA Wen-xia,SHAO Jin,YANG Qing.Calculation of Potential Distribution to 220 kV Icing Non-ceramic Insulators by Finite Element Method[J]. HighVoltage Engineering, 2007,33(4):21-25.
[8] MEKHALDI A,NAMANE D,BOUAZABIA S. Flashover of Discontinuous Pollution Layer on HvInsulators[J]. IEEE Transactions on Diclectrics and Electrical Insulation,1999,6(6):900-906.
[9] MEKHALDI A,NAMANE D,BOUAZABIA S,etal. Empirical Model of a High Voltage Insulator Undernon-UniformPollution[C]//Eleventh International Symposium on High voltage Engineering. London,UK:Academic Press,1999:4232-4235.
[10] ZHIU Yong,MASAHISA Otsubo,CHIKAHISA Honda.Mechanism for Change in Leakage Current Waveform on a Wet Silicone Rubber Surface:a Study Using a Dynamic 3-D Model[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2005,12(3):556-565.
[11] 高博,王清亮,周建博,等. 干燥带对污秽绝缘子电场分布的影响[J]. 高电压技术,2009,35(10):2421-2426.
GAO Bo,WANG Qing-liang,ZHOU Jian-bo,et al.Effect of Dry Band on Electric Field Distribution of Polluted Insulator[J]. HighVoltage Engineering,2009,35(10):2421-2426.
[12] 徐志钮,律方成,李和明. 分离水珠对支柱绝缘子电场分布的影响[J]. 高电压技术,2010,36(9):2278-2284.
XV zhi-niu,LV Fang-cheng,LI He-ming.Influence of Separated Globules on Post Insulator Electric Field Distribution[J]. HighVoltage Engineering,2010,36(9):2278-2284.
[13] 袁小娴,陈俊武,周志成,等. 330kV 线路复合绝缘子电位和电场分布的有限元计算[J]. 电瓷避雷器,2006,212(4):9-12.
YUAN Xiao-xian,CHEN Jun-wu,ZHOU Zhi-cheng,et al.A Finite Element Method for the Calculation of the Electric Field and Potential Distribution along the 330kV Line Composite Insulators[J].Ineulatorsand Surge Arresters,2006,212(4): 9-12.
[14] 徐其迎,李日隆. 110kV合成绝缘子沿面电场分布的研究[J]. 绝缘材料,2003,(4):48-50.
XU Qi-ying,LI Ri-long.Study on Calculating Electric Field of 110 kV Composite Insulator[J].Insulation Materials,2003,(4):48-50.
[15] 江汛,王仲奕,金强. 棒形悬式复合绝缘子电场计算和优化[J]. 高压电器,2004,40(3):215-217.
JIANG Xun,WANG Zhong-yi,JING Qiang.Calculation and Optimization of Electric Field and Voltage Distribution Along Long-rod Composite Insulators[J].High Voltage Apparatus,2004,40(3):215-217.
