城市轨道交通低频减振轨道结构研究

杨吉忠， 颜 华， 蔡成标

(1. 中铁二院工程集团有限责任公司 科学技术研究院， 四川 成都 610031;2. 西南交通大学 牵引动力国家重点实验室， 四川 成都 610031)

本文提出了一种被动式动力减振轨道结构，根据扩展定点理论[9-12]和车辆-轨道耦合动力学理论[1]，对该结构的关键设计参数进行了初步研究。

1 被动式动力减振浮置板轨道结构

被动式动力减振浮置板轨道结构通过在浮置板上附加一个弹簧-阻尼-质量子结构，利用附加质量和刚度构成的子系统把浮置板主体的振动能量吸收并加以增幅，并利用子系统的阻尼元素对振动能量加以消耗，见图1。基于扩展定点理论，利用最优同调和最优阻尼条件，得到抑制轨道结构1阶模态振动的最优刚度和阻尼，使附加质量块的振动相位与浮置板的振动相位相反，通过附加质量块的大位移振动，实现减小浮置板主体低频振动成分的目的。

2 扩展定点理论

轨道结构可视为由钢轨、扣件及轨下基础组成的三层连续离散点支撑梁模型[1]，其振动形态复杂，为具有多阶模态的连续振动系统。为简化计算，忽略轨道结构的阻尼影响，将其视为位于列车与线下基础间的一个单自由度质量-弹簧减振系统，被动式动力减振轨道简化力学模型见图2。图2中，M、m分别表示轨道板和附加质量块质量，x1、x2分别表示其振动位移；K、k分别为浮置板和弹性连接件的弹簧刚度；c为附加质量块的阻尼系数；Fsinωt为作用在浮置板主体上的正弦波激振力，F为激振力幅值。该系统的运动方程为

( 1 )

( 2)

( 3 )

式中:

Δ2=

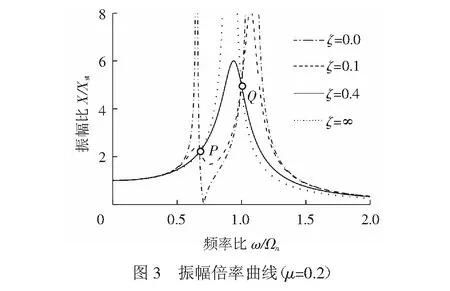
根据式( 3 )中不同ζ值得到的浮置板主体的振幅倍率曲线见图3，其中质量比取μ=0.2。从图3可以看出，不论ζ取何值，振幅倍率曲线均相交于P、Q点，且P、Q点振动相位相反。Erich Hahnkamm[13]在1932年发现了该现象，并利用这两个定点的特点推导出了最优同调的条件，即调整附加动力系统与主振系统之间的频率比，使P、Q等高。Brock[14]在最优同调关系的基础上，于1946年推导了最优阻尼的条件，即调整附加动力系统的阻尼与主振系统质量比之间的关系，将P、Q调整为振幅倍率曲线上的最大值。利用定点现象进行被动式动力减振系统设计的方法称为扩展定点理论[12]。

2.1 最优同调条件

由于P、Q为振幅倍率曲线上与ζ取值无关的固定点，对式( 3 )两侧取平方，并将ζ2之前的系数调整为1，得

( 4 )

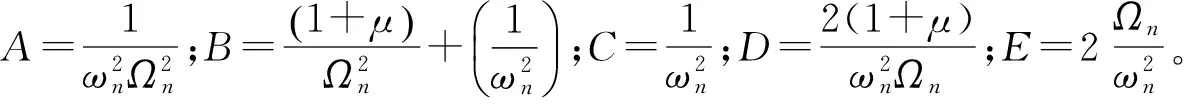
要使振幅倍率曲线与ζ的值无关，存在如下关系式

( 5 )

此时振幅比

( 6 )

式( 5 )整理为振动频率ω的方程

( 7 )

( 8 )

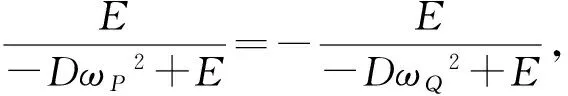
( 9 )

联立式( 8 )、式( 9 )，可得

2AE2=D(BE+D-EC)

(10)

将式(10)中A～E替换为ωn，Ωn和μ的多项式，可得到满足最优同调条件时的附加动力减振系统和主振系统的固有频率比为

(11)

2.2 最优阻尼条件

K4ζ4-K2ζ2+K0=0

(12)

式中：

K4=-2E2D2ω6+2DE3ω4

K2=(3A2E2+C2D2)ω8-(4ABE2+4CD2)ω6+

(B2E2+4CDE+3D2+2AE2-C2E2)ω4-

(4DE)ω2+(E2-E2)

K0=-2A2C2ω10+(2ABC2+6A2C)ω8-

(4A2+8ABC)ω6+(4AC+2B2C+6AB-2BC2)ω4-

(2C2-4A-2B2)ω2+(2B-2C)

舍去式(12)中ζ2的负数解，将ωP、ωQ代入式(12)，可得阻尼比ζP、ζQ

(13)

(14)

将ζP、ζQ的平均值定义为最优阻尼比ζopt，即

(15)

2.3 最优条件

同时满足最优同调条件和最优阻尼条件时，浮置板主体的最大振幅比为

(16)

对于被动式动力减振轨道结构，根据设计条件，附加质量块的质量m确定后，系统的质量比μ也就确定了。根据式(11)的最优同调及式(16)的最优阻尼条件，可得附加质量动力系统的设计参数。

(1) 附加动力系统的质量比

(17)

(2) 附加动力系统的弹簧刚度

(18)

(3) 附加动力系统的阻尼系数

(19)

3 车辆-轨道耦合系统的运动模型

3.1 车辆模型

基于车辆-轨道耦合动力学理论，车辆采用地铁标准B2型车，通过自编程序的方式实现车辆运行行为的模拟，其动力学模型及方程见文献[1]。轮轨接触模型中采用Hertz非线性弹性接触理论确定轮轨法向力，首先按照Kalker线性理论计算轮轨蠕滑力，然后采用沈式理论进行非线性修正。车辆模型的求解采用文献[1]提出的新型显式积分法。

车辆主要性能参数见表1，车辆运行速度取80 km/h。根据城市轨道交通轨道平顺性的特点，采用1～30 m波长范围的美国五级轨道谱作为车辆-轨道耦合系统的激励源。

表1 地铁B2型车性能参数

3.2 被动式动力减振浮置板有限元模型

基于有限元软件ANSYS建立短型钢弹簧浮置板轨道结构有限元模型，见图5。模型板长3.60 m，宽2.70 m，钢轨底部浮置板两侧厚度为325.00 mm。为了降低浮置板主体的固有频率，钢轨间浮置板厚度增加至475.00 mm，单块板下纵向每隔2组扣件设置2对钢弹簧减振器，减振器垂向刚度为7 kN/mm。模型中钢轨采用Beam188单元模拟，钢轨两端施加简支约束；浮置板采用三维实体单元Solid45进行模拟，在浮置板纵向两个端面施加对称约束模拟浮置板之间剪力铰对其纵向转动的约束作用；扣件和浮置板钢弹簧的刚度阻尼特性用Combine14单元模拟，并将浮置板钢弹簧底端施加固定约束。图4(b)为短型浮置板轨道的1阶模态图，其1阶固有频率为13.09 Hz。

根据被动式动力减振系统的最优设计条件式(17)～式(19)，质量比为0.1的被动式动力减振浮置板轨道结构与短型浮置板轨道结构的幅频曲线对比见图5。从图5可以看出，短型浮置板主体在13 Hz附近(1阶固有频率)的振动位移出现了非常明显的峰值，其振动位移达到27.20 mm；被动式动力减振浮置板主体在13 Hz附近的振动位移明显得到了抑制，仅为6.6 mm。被动式动力减振浮置板有效地抑制了短型浮置板固有频率处的振动。

4 低频减振特性分析

4.1 浮置板振动加速度

基于车辆-轨道耦合动力学理论，分析被动式动力减振浮置板轨道结构在列车荷载作用下的减振特性。质量比μ=0.1的被动式动力减振浮置板轨道与短型浮置板振动加速度对比见图6。从图6(a)可以看出，被动式动力减振浮置板的峰值明显比短型浮置板低。在计算范围内，短型浮置板主体最大振动加速度值为7.76 m/s2；采用被动减振技术之后，对应此时刻的浮置板主体振动加速度值为4.60 m/s2，降幅达40.72%。从图6(b)可以看出，短型浮置板轨道结构在13 Hz(1阶固有频率)附近出现了峰值；采用被动减振技术之后，浮置板主体在该频率处的振动加速度显著降低。因此，被动式动力减振浮置板可以有效地消除短型浮置板因共振产生的振动放大现象。

4.2 钢弹簧支点反力

轮轨作用力通过钢轨、扣件、浮置板、减振器层层衰减，传递至支撑基础结构上，钢弹簧支点反力反映的是传递至基础结构上的列车荷载。钢弹簧支点反力时程曲线和幅频曲线见图7。

图7(a)中，曲线的最大峰值表示列车车轮经过该弹簧支点时的作用力。被动式动力减振浮置板传递至基础支撑结构上的最大作用力较短型浮置板略小，但差别不明显。椭圆框内各个波谷表示车辆第2～3位轮对经过该支座时间段内的支座反力。被动式动力减振浮置板轨道结构对该时段内传递至基础支撑结构的作用力有较大的衰减，表明列车经过时首先引起浮置板主体的振动；作用力同时传递至基础支撑结构，浮置板主体振动引起附加质量块的较大位移振动，吸收并存储一定的振动能量，通过附加质量块与浮置板主体之间的连接阻尼逐渐将振动能量转换为内能，这就是被动式动力减振轨道结构的减振原理。

从图7(b)可以看出，短型浮置板的钢弹簧支点反力在其1阶固有频率13 Hz附近出现了较大的峰值，被动式动力减振浮置板的钢弹簧支点反力在13 Hz附近的峰值明显降低，从而有效降低了传递至基础支撑结构的低频振动。

4.3 质量比对减振效果的影响

从式(16)可知，浮置板主体的振动幅值与附加动力减振系统的质量比成反比，即质量比越大浮置板主体的振动幅值越小，振动得到抑制。为研究质量比对被动式动力减振浮置板轨道结构减振效果的影响规律，设计了4种不同质量比(μ=0.02～0.20)的被动式动力减振轨道结构，根据最优设计条件式(17)～式(19)，附加质量块的连接刚度和阻尼见表2。

表2 不同质量比对应的最优设计参数

短型浮置板和不同质量比的被动式动力减振浮置板振动加速度级对比及其插入损失见图8。从图8(a)可以看出，在1～30 Hz频率范围内，短型浮置板主体振动加速度级在13 Hz处最大；采用被动减振技术后，浮置板主体振动加速度级有较大的降低，随着质量比的逐渐增加，吸振效果逐渐增强。从图8(b)可以看出，质量比越大，插入损失也越大。质量比取最小值0.02时，被动式动力减振浮置板轨道的插入损失为5 dB；质量比取0.2时，其插入损失可达到12 dB。被动式动力减振浮置板轨道结构可以有效地抑制短型浮置板轨道结构在其1阶固有频率处的振动。

5 结论

针对城市轨道交通常规减振型轨道结构在低频域(<30 Hz)范围内因共振放大低频振动的现象，提出了一种被动式动力减振浮置板轨道结构。基于扩展定点理论和车辆-轨道耦合动力学理论，利用最优同调和最优阻尼条件，得到了抑制常规浮置板轨道1阶模态振动的最优刚度和阻尼。通过对短型浮置板轨道的数值仿真分析，可得出以下结论：

(1) 短型钢弹簧浮置板轨道结构因共振会放大13 Hz(其1阶固有频率)附近的振动。

(2) 被动式动力减振浮置板轨道结构可以有效地抑制13 Hz附近的振动。质量比为0.2时，被动式动力减振浮置板使13 Hz附近的振动降低12 dB，减小传递至基础支撑结构上的低频振动成分。

(3) 被动式动力减振浮置板轨道结构的质量比越大，浮置板主体振动加速度的插入损失越大，减振效果越明显。

参考文献：

[1] 翟婉明. 车辆-轨道耦合动力学[M].3版. 北京: 科学出版社, 2007.

[2] 北京市市政工程设计研究总院. 低频浮置板轨道: 中国, CN 102535260 B[P]. 2014-04-23.

[3] 马娜, 李成辉. 梯形轨枕竖向振动模态分析[J]. 工程力学. 2010, 27(5) : 247-256.

MA Na, LI CHENG-hui. The Vertical Vibration Modal Analysis of the Ladder Sleeper[J]. Engineering Mechanics, 2010, 27(5) : 247-256.

[4] 丁德云，刘维宁，张宝才，等. 浮置板轨道的模态分析[J] . 铁道学报,2008, 30(3) : 61-64.

DING De-yun, LIU Wei-ning , ZHANG Bao-cai, et al. Modal Analysis on the Floating Slab Track[J]. Journal of the China Railway Society, 2008, 30(3): 61-64.

[5] 李俊岭. 地铁钢弹簧浮置板轨道对环境振动的影响分析[D]. 成都：西南交通大学, 2011.

[6] 刘卫丰, 刘维宁, 聂志理, 等. 地铁列车运行引起的振动对精密仪器影响的预测研究[J]. 振动与冲击,2013, 32(8): 18-23.

LIU Wei-feng, LIU Wei-ning, NIE Zhi-li, et al.Prediction of Effects of Vibration Induced by Running Metro Trains on Sensitive Instruments[J]. Journal of Vibration and Shock, 2013, 32(8): 18-23.

[7] 刘卫丰, 刘维宁, 袁扬. 基于地铁列车运行引起的振动预测模型的浮置板轨道减振效果研究[J]. 铁道学报,2009, 34(9) : 81-86.

LIU Wei-feng, LIU Wei-ning, YUAN Yang. Study on Isolation Efficiency of Floating Slab Track Using a Numerical Prediction Model of Metro Traffic Induced Vibrations[J]. Journal of the China Railway Society,2009, 34(9) : 81-86.

[8] 刘卫丰, 刘维宁, 袁扬, 等. 地铁列车与道路车辆运行对环境的振动影响现场测试与分析[J]. 铁道学报,2013, 35(5) : 81-84.

LIU Wei-feng, LIU Wei-ning, YUAN Yang, et al.Study on Isolation Efficiency of Floating Slab Track Using a Numerical Prediction Model of Metro Traffic Induced Vibrations[J]. Journal of the China Railway Society, 2013, 35(5) : 81-84.

[9] 刘耀宗, 郁殿龙, 赵宏刚, 等. 被动式动力吸振技术研究进展[J]. 机械工程学报,2007,43(3):14-21.

LIU Yao-zong, YU Dian-long, ZHAO Hong-gang,et al. Review of Passive Dynamic Vibration Absorbers [J]. Chinese Journal of Mechanic Engineering, 2007, 43(3): 14-21.

[10] 盛美萍, 王敏庆, 孙进才. 噪声与振动控制技术基础[M]. 北京: 科学出版社, 2007.

[11] 背户一登. 动力吸振器及其应用[M]. 北京: 机械工业出版社, 2013.

[12] HARTOG J P D. Mechanical Vibrations[M].3rd ed. New York: McGraw-Hill, 1947.

[13] HAHNKAMM E. Die Dämpfung Von Fundämentschwin-gungen bei Veränderlicher Erregerfrequenz[J]. Ingenieur-archiv,1933,4(2):192-201.

[14] BROCK J E.A Note on the Damped Vibration Absorber[J]. Journal of Applied Mechanics,1946,13(4):A-284.