基于轮对模型的铁道车辆脱轨安全性评估
2015-05-10邬平波汪群生
魏 来, 曾 京, 邬平波, 高 浩, 汪群生
(西南交通大学 牵引动力国家重点实验室, 四川 成都 610031)
列车脱轨事故给人们的生命和财产安全造成巨大威胁。因此,国内外学者对脱轨问题开展了大量的研究。1896年,法国科学家Nadal[1]讨论了爬轨脱轨的力学条件,提出了脱轨系数的临界限值。日本铁路综研(RTRI)[2-4]研究了冲角对脱轨准则的影响,并利用1∶5滚动试验台进行验证。TTCI利用轨道加载车对轮对爬轨问题进行试验研究,认为爬轨脱轨决定于与脱轨系数有关的车辆走行距离,而不是脱轨持续时间[5-7]。Weinstock[8]采用爬轨侧车轮脱轨系数与非脱轨侧车轮脱轨系数之和作为爬轨脱轨准则。曾京[9-10]等通过轮对受力分析,推导了轮对爬轨脱轨和跳轨脱轨准则,但未考虑轮对侧滚的影响。
轮轨力测量是铁道车辆安全评估和健康监测的基础。测力轮对是最常用的轮轨力测量方式,通过测量轮轴和辐板变形实现轮轨力动态检测,但其标定工艺复杂且长期运用可靠性低。翟婉明等[11]在钢轨上布置应变片并组成特定桥路,测量车辆通过测力钢轨时的轮轨力。波兰的T.Uhl[12]根据轴箱加速度信号和脉冲响应函数反推出轮轨力;该研究在线性范围内进行,对轮轨横向力的识别存在较大误差。Xia[13]建立货车系统线性模型,通过车体加速度进行轮轨力反演识别,但简化线性模型对非线性车辆系统具有局限性。
本文基于轮对模型对铁道车辆脱轨安全性进行评估,包括基于轮轴脱轨系数和轮重减载率的爬轨脱轨准则以及轮轨力间接测量方法。基于该准则进行脱轨安全性评估,只需获取轮对的轮轴横向力和左右侧的轮轨垂向力即可。最后针对某客车车辆,进一步进行部分线路试验验证。
1 准静态轮对爬轨脱轨准则
根据轮对受力状态,考虑轮对侧滚角φ和摇头角ψ的影响,推导准静态轮对三维爬轨脱轨准则。轨道坐标系(xT,yT,zT)和轮对本体坐标系(xW,yW,zW)见图1, (xCL,yCL,zCL)和(xCR,yCR,zCR)分别表示轮对左右两侧的轮轨接触点坐标系[14]。

轮对侧滚旋转矩阵Aφ为
( 1 )
轮对摇头旋转矩阵Aψ为
( 2 )
轨道坐标系与轮对本体坐标系之间的变换关系为
[iTjTkT]T=AψAφ[iWjWkW]T
( 3 )
式中:iT,jT,kT为轨道坐标系的单位矢量;iW,jW,kW为轮对本体坐标系的单位矢量。轮对左右侧轮轨接触点处的旋转矩阵分别为
( 4 )
( 5 )
轮对本体坐标系与左右两侧轮轨接触点处坐标系关系为
[iTjTkT]T=AψAφAL[iTjTkT]T
( 6 )
[iTjTkT]T=AψAφAR[iRjRkR]T
( 7 )
式( 4 )~式(7)中:iL,jL,kL和iR,jR,kR分别为左右侧轮轨接触点坐标系的单位矢量;δL和δR分别为左右侧车轮接触角,假设左侧车轮为爬轨车轮。
轮对摇头角和侧滚角比轮缘角较小,则sinφ=φ,sinψ=ψ,cosφ=cosψ=1,据式( 6 )、式( 7 ),分别得轨道坐标系和左右接触点坐标系中轮轨力的变换关系
( 8 )
( 9 )
式中:TL、YL、QL和TR、YR、QR分别为轨道坐标系中左右轮轨接触点处的轮轨纵向力、横向力和垂向力,其受力见图1。FxL,FyL,NL和FxR,FyR,NR分别为左右接触点坐标系中的轮轨纵向力、横向切向力和法向力。式( 8 )中,轮轨横向力YL定义的方向与轨道水平坐标系中横向力FyL的方向相反,旋转矩阵第二行增加负号。
车轮脱轨系数Y/Q定义为轮轨横向力和垂向力的比值,可由式( 8 )推导出爬轨侧的轮轨脱轨系数
(10)
由式( 9 )推导出非爬轨侧的脱轨系数
(11)
左右接触点处的轮轨垂向力表示为
(12)
式中:Q为轴重之半;ΔQ为轮重减载量,轮重减载率定义为轮重减载量与轴重之半的比值。上式中,爬轨侧车轮出现减载,符号为负;非爬轨侧车轮出现增载,符号为正。
轮轴横向力H可表示左右轮轨横向力之和,即
H=YL-YR
(13)
轮轴脱轨系数定义为轮轴横向力与轴重之半的比值,根据上式可得到轮轴脱轨系数为
(14)
根据蠕滑理论可知
(15)
式中:r0为车轮半径;ri为左右接触点处的名义滚动圆半径。
轮轨横向切向力和法向力满足库伦摩擦定律
(16)
将式(15)、式(16)带入式(10)、式(11)、式(14)可得轮对爬轨脱轨准则
(17)
式中:
C1=
(18)
C2=
(19)
其中
(20)
式中:C1、C2、kL和kR为与轮轨接触参数相关的系数。若已知轮轴横向力和左右侧的轮轨垂向力,根据式(17)可进行轮对爬轨脱轨安全性评估。轮对的基本接触参数见表1。下面分析轮轨摩擦系数、轮对摇头角和轮缘接触角等参数对脱轨安全域的影响。

表1 轮轨接触参数
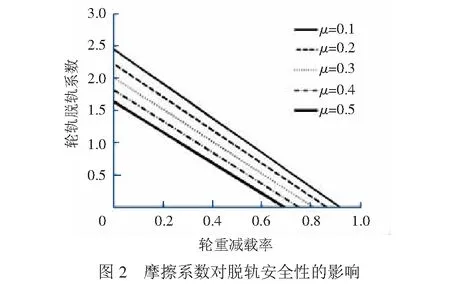
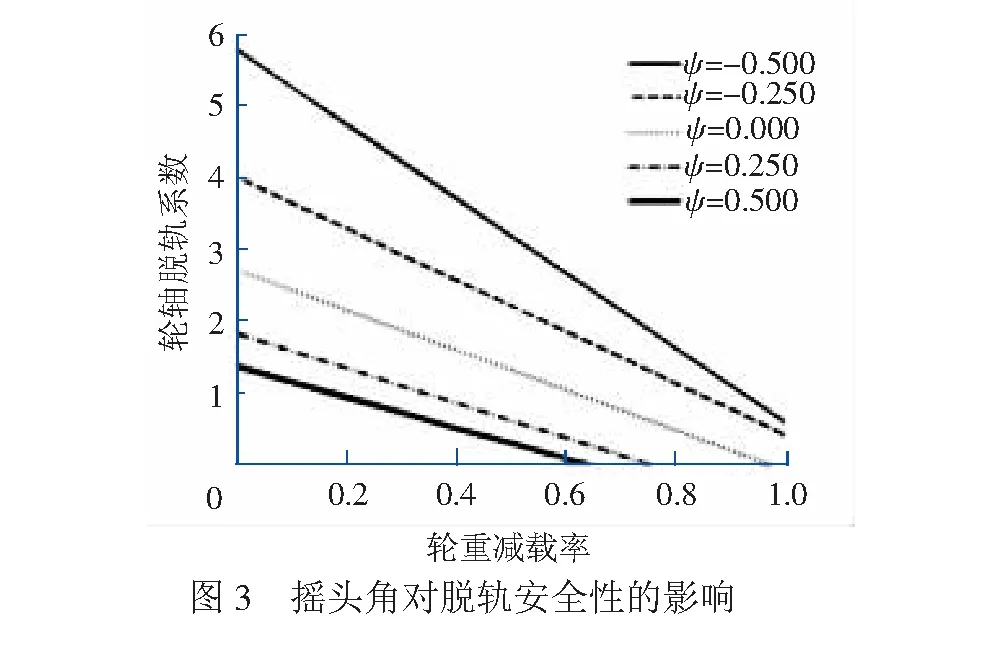
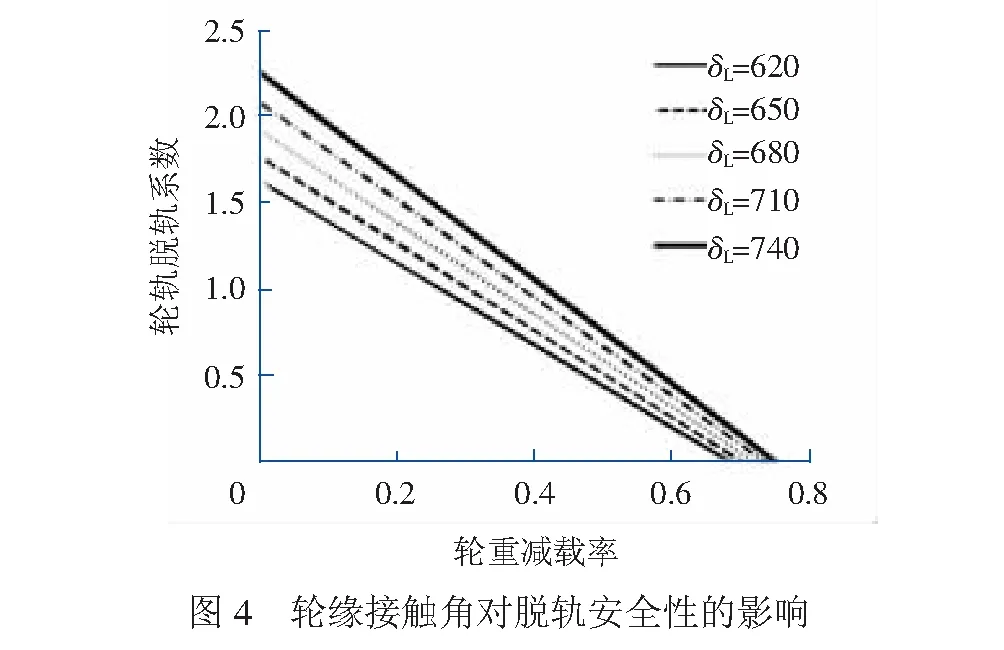
图2为轮轨摩擦系数对脱轨安全性的影响,可见轮轨摩擦系数越大,轮对脱轨安全域越窄,越容易发生脱轨。图3 为轮对摇头角对脱轨安全性的影响,随着摇头角增大,发生爬轨脱轨可能性增大;摇头角为负时,车轮的防脱轨能力提高。图4为爬轨侧的轮缘接触角对脱轨安全性的影响,增大轮缘接触角有利于增大脱轨安全域,提高防脱轨能力。
本文提出了基于轮轴脱轨系数和轮重减载率的脱轨评估准则,与传统Nadal准则在爬轨脱轨机理上等效。假设轮对处于脱轨临界状态时,结合轮对轮缘角、摇头角、轮轨摩擦系数等参数,可确定爬轨脱轨准则的临界值。
采用此准则进行脱轨安全评估,需要测定轮轨间的轮轴横向力和左右侧的轮轨垂向力,计算出轮轴脱轨系数和减载率。为此,本文进一步提出了一种基于轮对模型的轮轨力间接测量方法。
2 轮轨力间接测量方法
轮轨力测量是铁道车辆安全评估和状态监测的基础。传统方法采用测力轮对技术,即在车轮的轮轴和腹板位置粘贴应变片并组成特定的桥路,通过标定试验获得轮轨力和应变间接的系数,实现轮轨力的动态检测。但测力轮对成本较高,长期运用可靠性低。本文提出一种轮轨力间接测量方法,基于轮对模型建立横向力平衡方程和侧滚力矩平衡方程,通过加速度、位移和应变等物理量反推出轮轨力,单轮对受力分析见图5。

典型客车车辆的一系悬挂系统包括转臂定位节点、一系轴箱弹簧模型和一系垂向减振器等。车辆运行过程中,轮对受轮轨作用力、悬挂力、惯性力和重力的影响。根据轮对受力状态,建立横向力平衡方程
mway+2kydy+Fr1+Fr2+H=0
(21)
式中:mw为轮对质量;ay为轮对横向加速度;ky为一系轴箱弹簧横向刚度;dy为一系弹簧横向相对位移;Fr1和Fr2分别为左右 转臂定位节点横向力;H为轮轴横向力,即左右轮轨横向力之和。
转臂定位节点横向力的测量成为问题的关键,最直接办法是在轴箱转臂和构架之间安装位移传感器测量节点横向位移。但由于该位移幅值较小,传感器精度无法保证测试的准确性。本文提出一种节点横向力动态检测方法,通过在转臂上粘贴应变片,提前对轴箱转臂进行标定试验,获取关联不同位置应变和节点横向力的系数矩阵,从而根据实测应变得到节点横向力,见下式
Fri=kεεii=1, 2
(22)
式中:kε为节点横向力和应变之间的系数;εi为节点横向力引起的转臂弯曲应变,由式(21)和式(22)可得轮轴横向力为
H=-mway-2kydy-kεε1-kεε2
(23)
关于左右轮轨接触点分别建立轮对的侧滚力矩平衡方程,其中接触点变化相比横向跨距可忽略不计,未考虑轮对侧滚角加速度的影响。
mwazlc/2+(Qs1+Qd1)l1+Glc/2=
(Qs2+Qd2)l2+Q1lc-Hr0
(24)
mwazlc/2+(Qs2+Qd2)l1+Glc/2=
(Qs1+Qd1)l2+Q2lc+Hr0
(25)
式中:l1和l2定义为
(26)
一系弹簧垂向力Qsi为
Qsi=ksdzi
(27)
一系垂向减振器垂向力Qdi为
(28)
由式(24)、式(25)可确定轮对的左右侧轮轨垂向力为
G/2+mwaz/2+H·r0/lc
(29)
G/2+mwaz/2-H·r0/lc
(30)
根据式(23)、式(29)和式(30),通过测量轮对加速度、一系弹簧相对位移和轴箱转臂应变等物理量,并结合轮对固有参数,可反推出轮轴横向力和轮轨垂向力,轮轨力间接测量方法的具体实施流程见图6。

弹簧位移和速度的测试精度对轮轨力的反推至关重要,常用的位移测量装置主要包括拉线式、顶针式和激光式位移传感器,其中拉线式位移传感器无法实现横向和垂向的解耦,而且频响范围低;顶针式位移传感器可实现方向解耦,但频响也较低;建议采用激光式位移传感器,既能保证测试结果中不包含其他方向分量,还具有足够的频响带宽。另外构架和轮对的垂向相对速度可根据实测的一系垂向相对位移微分获得。本文建议采用的是激光式位移传感器,其测试精度达到0.015 mm,频响范围达到0~1 000 Hz,能够满足测试精度要求。
为了获得转臂定位节点横向力和轴箱转臂应变之间的转换系数,利用轴箱转臂试验台进行标定试验。由于本文通过在轴箱布置应变片进行转臂节点横向力的反推,因此轴箱转臂标定试验中应变片粘贴位置的选取至关重要。在标定试验过程中,在轴箱体内外表面不同截面处布置了大量应变片,同时沿着横向、垂向和纵向3个方向分别进行加载,根据各应变片变形敏感程度确定最终选取的测点,此外选取的测点需要仅对横向力引起的弯曲变形敏感而对纵向和垂向拉压变形不敏感,保证具有足够的方向解耦性。应变片的粘贴位置应视具体轴箱体结构而定,应变片的粘贴位置不具有普遍性。对于转臂式轴箱,应变片沿着纵向方向对称布置在轴箱上部的内外侧表面,同时可以组成双臂半桥桥路,消除温度和纵向拉伸的影响。转臂定位节点通过工装固定在试验台上,而另一侧与假轴过渡连接,液压作动器可通过假轴施加不同方向的作用力。作动器沿着不同方向施加的力与测得的转臂应变之间关系见图7,横向力变化范围为0~20 kN,垂向力变化范围为10~80 kN,纵向力变化范围为20~40 kN。

由标定试验可知,转臂应变随着横向力增大而增大,基本呈线性关系,见图7(a);说明轴箱转臂对横向力引起的弯曲变形敏感。而转臂应变与垂向力和纵向力也呈线性关系,但其产生的应变相比横向力产生的应变较小,见图7(b)和图7(c);说明轴箱转臂主要受横弯变形为主,对纵向和垂向拉压变形不敏感。由图7(a)可见,横向力引起的弯曲应变和横向力之间并非完全线性关系,因此实际力和应变对应关系采用的是分段线性函数。此外受台架试验条件的限制,轴箱标定试验中允许施加的最大横向力为20 kN,对于实际横向力超出20 kN情况,可通过线性插值获得其标定系数。建议完善标定试验工装并提高加载能力,确保横向力标定范围满足实际运用的需要。
3 试验验证
针对某高速客车进行线路试验,被试车辆安装了测力轮对和轮轨力间接测量装置。测试内容包括轮对横向和垂向加速度、一系弹簧横向位移、左右侧一系弹簧垂向位移和轴箱转臂应变。试验线路为一段环形铁道试验线,曲线半径为1 300 m,超高150 mm,试验速度为60 km/h,车辆处于过超高状态。根据实测的振动信号,按照上述的间接测量方法计算轮轨作用力,并与测力轮对实测值进行对比。
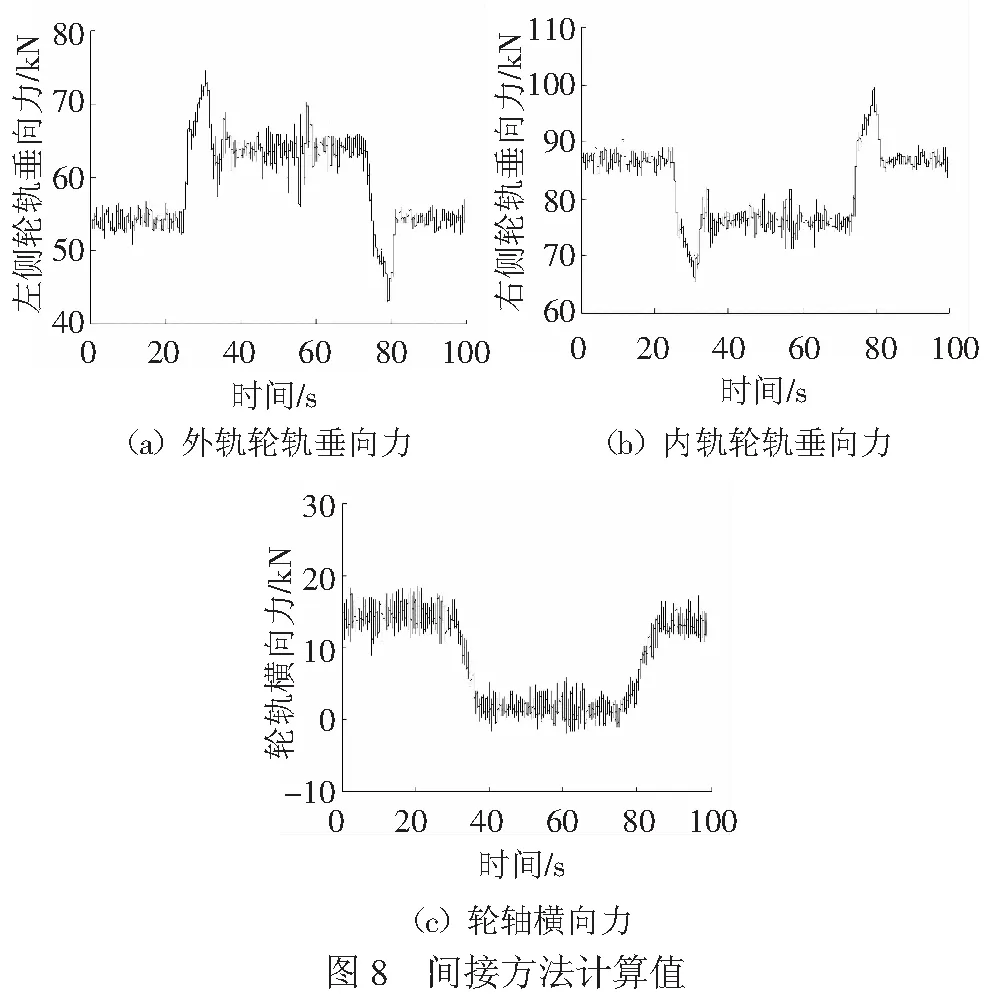

图8为轮轨力间接方法计算值,图9为测力轮对实测的轮轨力,包括外轨轮轨垂向力、内轨轮轨垂向力和轮轴横向力。可见,车辆从曲线段经过缓和曲线过渡到直线段时,轮轨垂向力产生冲击,而轮轴横向力变化平缓。对比可知,间接方法计算出的外轨轮轨垂向力最大值为74.57 kN,最小值为43.04 kN;测力轮对实测的外轨轮轨垂向力最大值为74.19 kN,最小值为44.85 kN;2种方法测得的外轨轮轨垂向力最大值和最小值的相对误差分别为0.5%和4.0%,见表2。间接方法计算出的内轨轮轨垂向力最大值和最小值的相对误差分别为0.4%和4.3%。间接方法计算出的轮轴横向力最大值的相对误差为11.2%。综上可见,相比测力轮对结果,间接测量方法波形吻合,峰值误差较低。
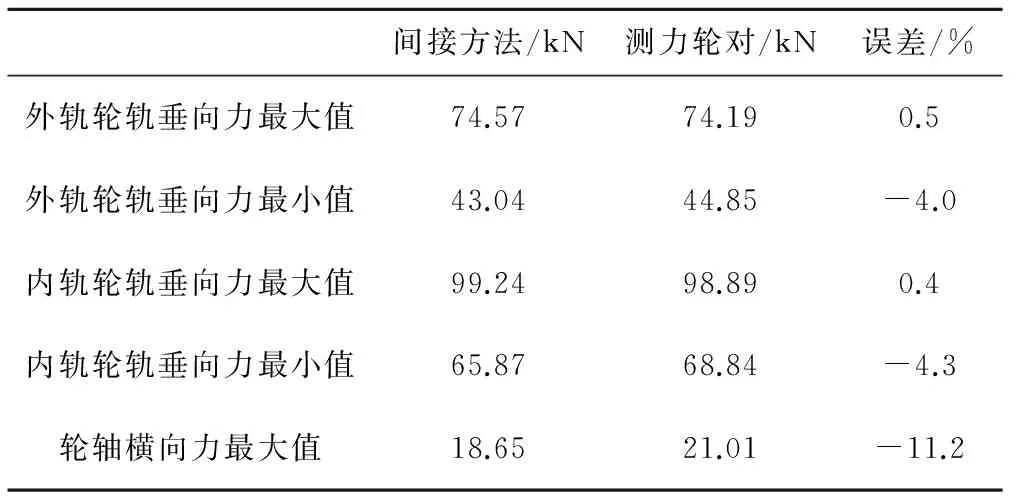
表2 试验结果对比
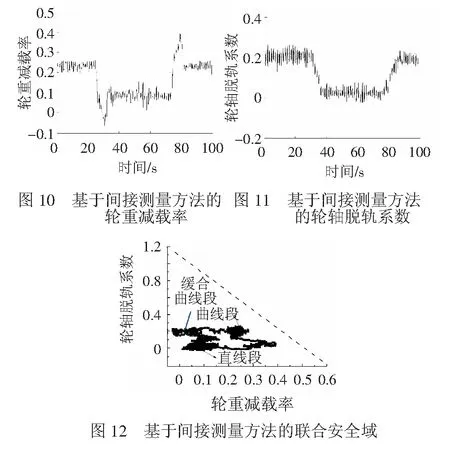
本文采用轮轴脱轨系数、轮重减载率及联合安全域分别进行脱轨安全性评估。针对轮轴脱轨系数或轮重减载率单个指标进行脱轨安全性评估时,文献[15]规定了采用构架力得到的脱轨系数限值为1.2,轮重减载率限值为0.65。图10和图11分别为间接测量方法得到的轮轴脱轨系数和轮重减载率,均未超过标准规定的限值。图12为采用二者联合安全域进行脱轨评估的散点图,其安全限值按照式(20)的轮对三维爬轨脱轨准则确定。可见,直线段的轮轴脱轨系数和轮重减载率均较低,进入曲线后二者均显著增大,缓和曲线段的轮重减载率逐渐增大而轮轴脱轨系数变化平缓。
本文提出的轮轨力测量方法及脱轨评估准则适用于低速或高速客车车辆,但是由于试验条件的限制,仅针对某高速客车进行了低速下的验证试验,也就是只对该方法进行了低速下的试验验证,下一步需要针对车辆高速运行情况下进行线路验证试验。
4 结论
(1) 本文推导轮对准静态爬轨脱轨准则,分析轮轨接触参数对脱轨安全域的影响,降低摇头角、减小摩擦系数以及增大轮缘接触角均有利于提高防脱轨能力。
(2) 提出一种轮轨力间接测量方法,根据轮对受力状态推导出轮轴横向力和轮对两侧轮轨垂向力的计算公式,采用转臂定位节点力动态检测技术获得节点横向力。
(3) 通过试验验证可知,间接测量方法获得的轮轨力与测力轮对实测值波形吻合,轮轴横向力和轮轨垂向力误差分别为11.2%和4.3%,能够满足工程运用的要求。
(4) 该轮轨力间接测量方法的局限性在于仅适用于带一系转臂定位节点和轴箱弹簧结构的车辆,且采用轮轴脱轨系数和轮重减载率联合安全域进行安全性评估。
参考文献:
[1] NADAL M J. Locomotivesa Vapeur, Collection Encyclopedie Scientifique[J] . Bibliotheque de Mecanique Appliquee et Genie, 1908,186(1):56-67.
[2] MIYAMOTO M, SUDA Y. Recent Research and Development on Advanced Technologies of High-speed Railways in Japan[J]. Vehicle System Dynamics, 2003,40(1-3):55-99.
[3] YOKOSE K. A Theory of the Derailment of Wheelset[J]. Railway Technical Research Institute,1966,7(3):30-34.
[4] MATSUO M. Quasi-static Derailment of a Wheelset[J]. Railway Technical Research Institute,1986,27(3):94-97.
[5] ELKINS J, WU H. Angle of Attack and Distance-based Criteria for Flange Climb Derailment[J]. Vehicle System Dynamics, 1999,33(S):293-305.
[6] WU H. Investigation of Wheel/Rail Interaction on Wheel Flange Climb Derailment and Wheel/Rail Profile Compatibility[D]. Chicago: Illinois Institute of Technology, 2000.
[7] SHU X, WILSON N, WU H, et al. A Bi-parameter Distance Criterion for Flange Climb Derailment[C] //ASME/ IEEE 2005 Joint Rail Conference. Pueblo: American Society of Mechanical Engineers, 2005: 9-17.
[8] WEINSTOCK H. Wheel Climb Derailment Criteria for Evaluation of Rail Vehicle Safety[C]//Proceedings of the ASME Winter Annual Meeting. New York: American Society of Mechanical Engineers,1984, 84: 1-7.
[9] ZENG J, WU P. Study on the Wheel/Rail Interaction and Derailment Safety[J]. Wear, 2008, 265(9): 1452-1459.
[10] ZENG J, GUAN Q H. Study on Flange Climb Derailment Criteria of a Railway Wheelset[J]. Vehicle System Dynamics, 2008, 46(3): 239-251.
[11] 翟婉明.车辆-轨道耦合动力学[M].北京:中国铁道出版社,1997:74-80.
[12] UHL T. The Inverse Identification Problem and Its Technical Application[J]. Archive of Applied Mechanics, 2007, 77(5): 325-337.
[13] XIA F, COLE C, WOLFS P. An Inverse Railway Wagon Model and Its Applications[J]. Vehicle System Dynamics, 2007, 45(6): 583-605.
[14] 曾京, 关庆华. 铁道车辆运行安全评判的轮对爬轨脱轨准则[J]. 交通运输工程学报, 2008, 7(6): 1-5.
ZENG Jing, Guan Qian-hua. Wheelset Climb Derailment Criteria for Evaluation of Railway Vehicle Running Safety[J]. Journal of Transportation Engineering, 2008, 7(6): 1-5.
[15] 中国国家标准局. GB 5599—1985铁道车辆动力学性能评定和试验鉴定规范[S]. 北京:中国标准出版社,1985.
