基于信息熵的列控系统复杂性度量方法

崔鹏亮， 王海峰 ， 陈建译， 徐田华

(1. 北京交通大学 轨道交通运行控制系统国家工程研究中心，北京 100044；2. 广州铁路(集团)公司 电务处，广东 广州 510000；3. 北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044)

列控系统作为高速铁路的中枢神经系统，是保证列车运行安、提高运输效率的核心技术装备。借鉴国外高速铁路列控系统建设运用的经验和ETCS的发展理念，结合我国铁路运输的特点及既有信号设备的制式，制定了中国列车运行控制系统(CTCS)，解决了中国铁路信号系统统一技术标准的难题。

当今的列控系统规模越来越大、复杂性越来越高，离散计算和连续物理过程紧密耦合，运行环境从封闭静态环境延伸到了开放、动态、持续演化的分布式网络化环境，存在大量的不确定性因素和异构子系统。实际运营过程中，由于现场人员对列控系统复杂性缺乏透彻清晰的理解，造成安全环节不易把控，运营维护面临巨大压力。在对列控系统体系结构进行优化设计时，由于缺乏系统复杂性方面的定性分析和定量计算手段，不易把控其中的关键环节。

复杂大系统的出现促进了人们对复杂性问题的研究。Kolmogorov提出了描述复杂性，用描述符号序列的最短程序长度来度量该序列的复杂程度[1]，但在具体应用时，理论上存在不可计算的问题。Wolfram 以形式语言理论为基础，用元胞自动机状态的个数来度量动力系统的复杂性[2]。Crutchfield和Young提出了基于统计力学的统计复杂性，在此基础上，将随机因素引入自动机，构造随机自动机ε机，以ε机的计算能力度量动力系统的复杂程度[3-4]，但是构造ε机是一个建模的过程，计算量非常大。Cramer将复杂性定义为系统可能状态数目的对数[5]，对于同一个系统，系统可能存在状态的数目又随着对系统描述的角度不同而不同，从而得到的系统复杂性也不同，因此，这样定义复杂性具有一定的主观性。Shinner基于有序度与无序度，给出一种系统通用的复杂性度量方法[6]，这个方法简单，但是太过于笼统，不能反映系统的内在特征。文献[7]运用5种指数度量系统结构复杂性， 这些指数都是从心理学的角度提出的，是对复杂性的一种定性刻画，定量化程度不是很高。

1948年Shannon提出信息熵理论，在复杂性度量方面得到了广泛的应用[8-12]。信息熵主要用于度量信息的不确定性，可以表示系统的复杂性，系统的熵值越大，表示系统越复杂，适用于分析系统在信息传输过程中存在不确定性的问题。系统的熵值影响因素包括：系统中元素的数量、类型以及元素之间关系的复杂程度。列控系统中的设备环节多，设备之间的接口关系复杂，并受外界因素干扰，运行状态具有一定的不确定性。因此，本文应用信息熵理论度量列控系统的复杂性，基本思路是：首先分析列控系统的复杂性，确定列控系统复杂性度量指标；然后，基于信息熵理论给出每一个度量指标的具体计算公式；最后，通过实例验证所提出复杂性度量模型的合理性和实用性。

1 CTCS-3级列控系统

CTCS-3是基于无线通信的列车运行控制系统，由地面设备和车载设备组成。地面设备包括：列控中心(TCC)、无线闭塞中心(RBC)和临时限速服务器(TSRS)等；车载设备包括：车载安全计算机、人机接口单元、测速测距模块、应答器信息接收模块、轨道电路信息接收单元和无线通信单元等，见图1。

由于联锁系统和调度集中(CTC)与列控系统密不可分，因此，在对列控系统复杂性进行定量分析时，将联锁系统与CTC纳入分析范围。

GSM-R实现了车-地信息的双向传输；车载设备主要负责接收地面传输的控车信息，生成速度防护曲线；TCC作为后备模式CTCS-2列控系统地面设备的核心部分，根据联锁进路信息、轨道区段占用信息、线路限速信息等，生成控车命令；RBC根据列车占用情况及进路状态向所管辖的列车发送行车许可命令和列车控制信息；联锁系统主要负责向TCC、RBC提供进路信息，并接受来自于RBC的行车许可状态及列车相关状态；ZPW-2000轨道电路主要完成列车占用检测和完整性检查。

2 列控系统复杂性

一般而言，系统科学中的复杂性泛指子系统与子系统之间、子系统与系统之间、要素与要素之间、要素与系统之间的关系呈现出的各种不确定性，以及系统与外部环境之间的关系呈现的各种不确定性[13]。文献[14]指出复杂系统是由大量不同的相互作用的单元组成的系统，复杂性研究的内容是研究复杂系统是如何在一定的规则下产生有组织的行为。文献[15]指出复杂性实际上是开放的复杂巨系统的动力学，是开放的复杂巨系统的特征。

结合列控系统的特殊性，本文列控系统复杂性是指列控系统在建设、运行和维护过程中，由于系统的设计体系结构、线路上列控系统的配置以及运行状态造成系统建设和运营维护的困难程度。本文从系统结构、功能分配和过程控制逻辑3个方面对列控系统复杂性进行度量分析，具体的列控系统复杂性度量参数见图2。

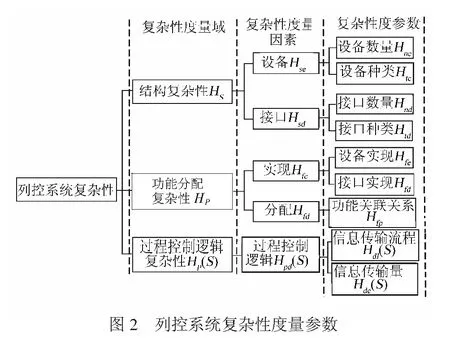
结构复杂性是指组成列控系统的设备、接口关系的多样性和异质性。与设备、接口的数目和种类有关，列控系统中的设备和接口数目越多，种类越多，系统结构越复杂。列控系统结构复杂性是由系统设计带来的，但是列控系统并不是一个固定不变的系统，而是一个涉及所有铁路线路以及线路上运行的所有列车的复杂系统，与线路、车站的布局、动车组以及运输组织等因素相关[16]。因此，度量列控系统结构复杂性需要针对某一段特定的线路，选取的线路不同，度量的结果也不一样。

功能分配复杂性是指列控系统在运行过程中，实现某一特定的功能时所需设备、接口的多样和差异性，以及同一设备承担两种或两种以上功能的关联性。

过程控制逻辑复杂性是指列控系统在不同的运营场景下，执行相应的操作命令时，设备之间进行相互通信的逻辑关系。过程控制逻辑复杂性与行车过程和线路配置有关，是随着列车的运行而不断变化的。

3 列控系统复杂性度量模型

信息熵是用于度量信息量的一个概念，系统越混乱，信息熵越大，反之，系统越有序，信息熵越小。信息熵定义为

( 1 )

式中：X={x1，x2，…，xn}为随机事件；p(xi)为随机事件xi发生的概率。

3.1 结构复杂性度量

列控系统中的设备和接口关系都是对列控系统结构的描述，可以反映列控系统的部分特征。但度量列控系统结构复杂性时，不能直接运用这两个要素，必须对这两个要素加以抽象，使它们符合度量要求。复杂网络理论将复杂系统中的元素抽象为节点，元素之间的相互关系抽象为边，为研究复杂系统提供了一个更加简单的描述方式[17]。因此，首先对列控系统进行抽象描述，然后从设备和接口方面度量系统的结构复杂性，最后再利用正交投影法对结构复杂性统一评价。

(1) 设备

一般而言，组成系统设备的数量越大，种类越多，系统结构越复杂。因此，将设备数量和设备种类作为列控系统结构复杂性的度量参数。

假设某一段线路上配置的列控系统中，设备数目为NE，设备的种类为TE，对配置的列控系统进行抽象描述，即节点关系图中节点的数目为NE，节点的种类为TE。在节点关系图中，节点的度定义为节点的邻边个数，关联矩阵可描述节点和各个边之间的邻接关系，所以节点的度可以用关联矩阵计算。

配置的列控系统中，所有设备数目的复杂性参数Hne为

( 2 )

配置的列控系统中，所有设备种类的复杂性参数Hte为

( 3 )

式中：ni为第i类节点的数目；di为第i类节点的度。

(2) 接口

当系统中的设备一定时，设备之间的接口越多，系统结构越复杂。故接口数量和接口种类可作为列控系统结构复杂性的度量参数。

假设某一段线路上配置的列控系统中，接口数目为ND，接口种类为TD，对配置的列控系统进行抽象描述，即节点关系图中边的数目为ND，边的种类为TD，配置的列控系统中，所有接口数目的复杂性参数Hnd为

( 4 )

配置的列控系统中，所有接口种类的复杂性参数Htd为

( 5 )

式中：mi为第i类边的数目。

(3) 结构复杂性

通过以上方法可以求出列控系统结构复杂性各个度量参数的熵值，根据图2中列控系统结构复杂性度量参数可知，列控系统结构复杂性度量是一个多维度度量问题。

正交投影法可对系统不同层次各个复杂性指标进行统一评价[18]，它的基本原理是：利用系统结构不同层次的各个复杂性熵值构成多个熵值向量，然后对这些熵值向量进行正交变换，从而滤去每一个熵值向量的重复信息，基于此，搭建理想熵值向量，获得多个熵值向量的投影值，将各个层次的熵向量投影值作为相应层次复杂性的统一评价指标，用于表示系统不同层次的复杂程度，所有层次的熵向量投影值总和反映了系统整体的复杂性。通过分析各个层次熵值向量的特征值和特征向量，确定出原来复杂性度量指标对于总体复杂性的权重，权重比较大的度量指标就是影响系统结构复杂性的主要因素。

基于正交投影法，建立列控系统结构复杂性的多维矢量空间度量模型，具体的步骤为：

Step1假设将列控系统结构复杂性的某一个度量指标分为u个层次进行度量，第i个层次有vi个影响因素，第i层第j个影响因素有vij个复杂性度量参数，其中第k个复杂性熵值为Hijk，将第i层第j个影响因素的所有复杂性熵值求和，第i层就构成了一个vi维空间向量bi，称该向量为熵值向量，令v=max{vi}，对于维数vi小于v的熵值向量bi，可用0元素补齐，因此，u个v维熵值向量就可以构成一个矩阵B，称之为熵值矩阵，即

( 6 )

Step2求解得到矩阵BTB的特征值为1,2,…,u(i>=0,i=1, 2, … ,u)，对应的特征向量为α1,α2,…,αu，这些特征向量均为单位正交向量，令C=[α1,α2,…,αu]，对熵值矩阵B进行正交变换，得到新的熵值矩阵Y，即

Y=BC=[yij]u×v

( 7 )

Step3搭建理想熵值向量y*=[y1,y2,…,yu]，务必保证

yj=max{yij}=max{|yij|}

j=1,2,…,v

( 8 )

如果max{yij}≠max{|yij|}，则相应的特征向量αj取反号，熵值矩阵Y对应的第j列向量也随之取反号。

Step4对搭建的理想熵值向量y*单位化得

( 9 )

Step5求解各熵值向量yi在理想熵值向量上的投影值

i=1,2,…,u

(10)

Step6求列控系统结构复杂性度量参数的熵值

(11)

Step7求各个复杂性熵值对列控系统结构复杂性的权重

Q=[q1,q2,…,qv]=

[λ1,λ2,…,λu]·[α1,α2,…αu]T

(12)

Step8对Q进行归一化处理，得出每一个复杂性熵值的权重，即

(13)

式中：w1，w2，…，wv分别为原复杂性熵值b1,b2,…,bv对应的权重。

3.2 功能分配复杂性度量

列控系统的主要功能是保证线路上运行列车的进路安全，控制列车运行速度。列控系统包含许多设备，为实现某一个特定功能，需要分配一些特定的设备彼此进行相互通信。如何实现所需的功能，如何根据功能对设备进行合理分配，将会到直接影响列控系统功能的复杂性。因此，从功能实现和功能分配两个方面对列控系统功能复杂性进行度量。

(1) 功能实现

列控系统主要实现行车指挥、速度防护、进路控制和行车许可4个功能，实现每一个功能需要许多设备去完成，设备之间需要频繁的进行通信，当完成某一个功能时，需要的设备越多，设备之间通信接口越多，实现该功能就越复杂。所以，将设备实现和接口实现作为功能实现的复杂性度量参数。

列控系统实现所有功能时，设备实现复杂性参数为

(14)

列控系统实现所有功能时，接口实现复杂性参数为

(15)

式中:NF为列控系统需要实现功能的数目；Ei为实现第i个功能时，需要的设备数目；Dij为实现第i个功能时，第j个设备与其它设备之间的接口数目。

(2) 功能关联关系

在列控系统中，某一些设备参与完成两个或两个以上的功能，将该设备与相应所完成的功能之间关系称之为功能关联关系，从而，列控系统中的所有设备与完成的功能之间相互关联，构成关联矩阵

(16)

当第i个设备与第j个功能存在关联关系时，aij=1；否则aij=0。

设备与功能的关联关系越多，系统功能就越复杂性，因此，可以用功能关联关系度量列控系统的功能分配复杂性。则功能关联关系复杂性参数为

(17)

式中:m为列控系统中设备类型的总数目；n为列控系统所需完成的功能总数目，则列控系统的功能分配复杂性HF为

HF=Hfe+Hfd+Hfp

(18)

3.3 过程控制逻辑复杂性度量

列控系统的运营场景简要描述了列车在运行过程中车载设备和地面设备之间的协作关系，CTCS-3列控系统共设置了RBC切换、等级转换、临时限速、行车许可和自动过分相等14种运营场景。列车在运行过程中，列控系统地面设备实时从现场获取信息，然后经过多次逻辑运算和传输，最后发送给车载设备，同时，车载设备将列车信息发送给地面设备，地面设备和车载设备之间频繁的进行信息交互，从而控制列车安全运行。当列车处于不同的运营场景时，地面设备和车载设备之间信息的传输流程和逻辑运算是不同的，而且传输的信息量也是不断变化的。信息传输经过的中间环节越多，行车过程就越复杂；信息交换越频繁，传输信息量越大，行车过程也就变得复杂。因此，以信息传输流程和信息传输量为复杂性度量参数，分析在列车运行过程中列控系统的复杂性。

列车在s到s+Δs(s和s+Δs均表示列车运行位置)这段区间内运行时，列控系统信息传输流程的复杂性参数为

(19)

在列车运行过程中，列控系统信息传输量的复杂性参数为

Hpu(s)=

(20)

式中:NP(s)为车地之间信息交互的次数；TMi(s)为第i次交互信息时，包含信息的种类；Lij(s)表示第i次交互信息时，第j种类型的信息传输所经过的环节数目；Uij(s)为第i次交互信息时，第j种类型的信息传输所含的信息量。

列车在s到s+Δs这段区段内运行时，列控系统过程控制逻辑复杂性HP(s)为

HP(s)=Hpl(s)+Hpu(s)

(21)

4 武广高铁线路实例分析

武广高铁线路全长1 068.8km，共18个车站、53个中继站、2个线路所，全线配置18个联锁系统、18个车站列控中心、53个中继站列控中心、2个线路所列控中心、9个RBC、4个临时限速服务器、2个CTC、18个CTC车站分机。为验证模型的合理性和实用性，结合列控系统的特点，从影响列控系统复杂性的因素出发，针对相同线路，以及系统需求相同的条件下，分析不同系统配置方案的复杂性。为此，选取武广线上清远站至广州南站的一段线路，该段线路上有3个车站，约83km。并对该段线路提出以下两种系统配置方案。

方案1对此段线路配置3个联锁系统、3个车站TCC、4个中继站TCC、2个RBC、2个TSRS、2个CTC、3个CTC车站分机。

方案2现有CTCS-3系统中，车站TCC功能相对比较单一，本方案将车站TCC的功能分配给联锁系统，所选线路配置3个联锁系统、4个中继站TCC、2个RBC、2个TSRS、2个CTC、3个CTC车站分机。

下面从系统结构、功能分配和过程控制逻辑3方面对比较两种系统配置方案的复杂性。

4.1 结构复杂性对比

度量列控系统结构复杂性时，需要对线路上配置的列控系统结构进行抽象描述，因此，针对所选线路上配置的列控系统，将设备抽象为节点，设备之间的通信接口抽象为边，方案1和方案2抽象后，系统节点关系分别图3、图4。

图3中个符号代表的节点分别为：e4、e16、e31为连锁系统；e1、e8、e11、e15、e22、e25、e29为ZPW2000轨道电路；e36、e39为TSRS；e43为无线通信单元；e3、e18、e32为车站CTC；e2、e9、e14、e17、e23、e28、e30为轨旁电子单元；e37、e40为CTC；e44为CTC-3控制单元；e48为司法纪录单元；e6、e19、e33为车站CTC分机；e5、e10、e13、e20、e24、e27、e34为微机监测单元；e41为轨道电路接收单元；e49为 CTC-2控制单元；e35、e38为RBC；e7、e12、e21、e26为中继站CTC；e42为应答器接收模块；e46为列车接口单元；e45为人机接口单元；图4中个符号代表的节点分别为：e4、e16、e31为连锁系统；e1、e8、e11、e15、e22、e25、e29为ZPW2000轨道电路；e36、e18为TSRS；e40为无线通信单元；e6、e19、e33为车站CTC；e2、e9、e14、e17、e23、e28、e30为轨旁电子单元；e32、e37为CTC；e41为CTC-3控制单元；e45为司法纪录单元；e6、e19、e33为车站CTC分机；e5、e10、e13、e20、e24、e27、e34为微机监测单元；e38为轨道电路接收单元；e46为 CTC-2控制单元；e35、e3为RBC；e7、e12、e21、e26为中继站CTC；e39为应答器接收模块；e43为列车接口单元；e42为人机接口单元；由图3、图4可以获得不同系统配置方案的一些结构参数，按照式( 2 )～式( 5 )，可以得出方案1和方案2结构复杂性度量因素的参数值，其结果见表1。

表1 方案1和方案2结构复杂性度量因素的参数值

根据式( 6 )，结合表1计算出的结构复杂性度量因素的参数值，可以分别得出方案1和方案2结构复杂性度量因素参数值构成的熵值矩阵，分别用B1和B2表示，即

针对方案1和方案2，由式( 7 )～式(13)得到相应的结构复杂性，结果表2。其中w1表示设备和接口的数目对于结构复杂性的贡献权重，w2表示设备和接口的种类对于结构复杂性的贡献权重。

表2 方案1和方案2结构复杂性度量的参数值

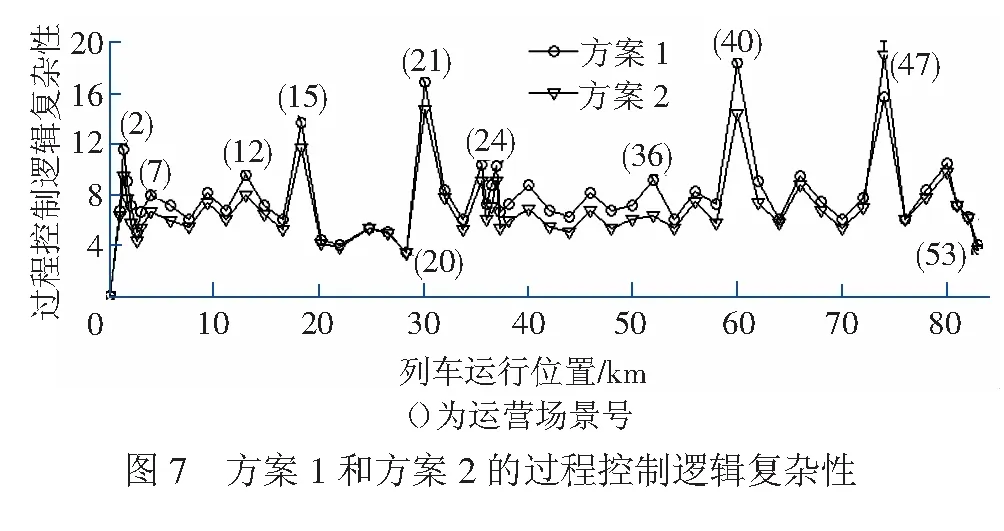
从表2中可以看出，方案1的结构复杂性为42.659，而方案2的结构复杂性为31.321。由于车站TCC牵涉的接口较多，与方案1相比，方案2将车站TCC功能整合到联锁系统，所以方案2的设备接口数目、种类均小于方案1。因此，方案1的结构复杂性明显小于方案2，符合直观判断。在方案1和方案2中，均满足w1

4.2 功能分配复杂性对比

根据式(14)～式(18)，可以得出方案1和方案2的功能分配复杂性度量参数值，见表3。

表3 方案1和方案2的功能分配复杂性度量参数值

由表3可知，方案1的功能分配复杂性为39.399，而方案2的功能分配复杂性为33.227。由于车站TCC和联锁系统之间的耦合性较高，在实现相应功能时，牵涉的设备、接口多，而将它们整合以后，设备、接口数量有所降低。因此，方案2配置的功能分配复杂性小于方案1。

4.3 过程控制逻辑复杂性对比

以选取的线路为基础，假设列车从清远站发车，在广州北站办理通过进路，运行到广州南站接车，并在列车运行过程中，设置一些运营场景，见图5，图中省略了正常情况下的一些区间行车许可运营场景。下面分析比较列车在运行过程中，方案的过程控制逻辑复杂性。

首先以列车运行在18.4 km处(即CTCS-3至CTCS-2等级转换)为例，说明列控系统过程控制逻辑复杂性的计算过程。当离开CTCS-3区域，从CTCS-3进入CTCS-2区域时，车地之间交换的信息时序图见图6，FS表示完全监控模式，OS表示目视行车模式。

根据图6所示的车地信息交互时序图，结合信息传输流程，可以获取计算等级转换过程中控制逻辑复杂性所需要的数据，见表4。

表4 等级转换过程中信息交互次数、传输环节数和信息传输量

NP(s)TMi(s) Lij(s)Uij(s)/bit——行车许可688——应答器链接212815线路坡度278——线路速度286——等级转换29721位置报告信息213731位置报告信息213741通信会晤管理211351通信会话结束27461通信会话结束确认275

根据式(19)，结合表4中的数据，可以得出列控系统信息传输流程的复杂性参数为

Hpl(s)=11.324

根据式(20)，可以得出列控系统信息传输量的复杂性参数为

Hpu(s)=2.299

根据式(21)，可以得出在CTCS-3至CTCS-2等级转换过程中，过程控制逻辑复杂性为

HP(s)=Hpl(s)+Hpu(s)=

11.324+2.299=13.623

同理，可以计算出列车处于不同运营场景时，方案1和方案2的过程控制逻辑复杂性，其结果见图7，图7中标出了过程控制逻辑复杂性较大(或较小)时对应的运营场景号，如“(15)”、“(20)”等。

通过对图7分析，可以得出以下结论：

(1) 对于不同配置方案，RBC切换(60 km处，运营场景号为40)时，方案2的过程控制逻辑复杂性明显小于方案1。由于方案2中的联锁系统整合了车站TCC的功能，RBC切换时，接管RBC所需轨道区段占用信息可以直接从两个联锁系统(前一个车站的联锁系统和后一个车站的联锁系统)中获取，所以，与方案1相比，方案2的轨道区段占用信息传输减少了两个环节。因此，RBC切换时，方案2的过程控制逻辑复杂性明显小于方案1。但是，临时限速(74 km处，运营场景号为47)时，方案2的过程控制逻辑复杂性大于方案1。因为方案2将车站TCC功能整合到联锁系统，当临时限速时，联锁系统既要处理进路控制信息，还要完成原有车站TCC的限速功能(后备模式CTCS-2控车时，车站TCC实时编码，通过轨旁电子单元向列车发送限速信息)，因此，临时限速时，方案2的过程复杂性大于方案1。在其它运营场景处，方案1的过程控制逻辑复杂性略大于方案2。由于方案2将车站TCC的功能整合到联锁系统，RBC计算移动授权时，所需要的轨道区段占用信息减少了一个中间传输环节，因此，与方案1相比，方案2的过程控制逻辑复杂性有所减小。

(2) 对于同一配置方案(如方案1)而言，过程控制逻辑复杂性是随着列车运行位置的变化而不断变化的。当列车处于RBC切换(60 km)时，方案1的过程控制逻辑复杂性达到最大值18.318；当列车分别处于CTCS-3至CTCS-2等级转换(18.4 km)、CTCS-2至CTCS-3等级转换(30.2 km)和临时限速(74 km)时，CTCS-3过程控制逻辑复杂性分别达到了局部极大值13.623、16.784和15.648。而当列车处于一般的行车许可运营场景(如4 km)时，过程控制逻辑复杂性为7.892。其原因是：当列车分别处于RBC切换、CTCS-2至CTCS-3等级转换、临时限速、CTCS-3至CTCS-2等级转换和行车许可(如4 km)时，车地之间的信息传输量和信息传输环节总数是依此递减的，根据文献[19]可知，总的信息传输量分别为3 135、2 387、1 511、1 013、526 bit，信息传输环节的总数分别为34、30、26、24、10。因此，过程控制逻辑复杂性变化与信息传输量和传输环节数的变化一致，度量结果与实际相吻合。

5 结束语

本文基于信息熵理论，从结构、功能分配和过程控制逻辑复杂性3个方面对列控系统复杂性进行度量。建立了复杂性度量模型，给出了各个指标的复杂性计算公式。利用正交投影方法，解决了结构复杂性的多维度度量问题。以武广高铁部分线路为例，从结构、功能分配和过程控制逻辑3个角度，分析了列控系统不同配置方案的复杂性。结果表明：设备接口数量和接口种类的差异性，是影响系统结构复杂性的关键因素；某一时刻同时参与控车的设备数量，是影响功能分配复杂性和过程控制逻辑复杂性的重要环节。本研究对提高我国列控系统运营过程的安全把控能力，进一步优化系统有借鉴意义。

参考文献：

[1] KOLMOGOROV A.Three Approaches to the Quantitative Definition of Information[J].Problems of Information Transmission,1965,1(1):1-7.

[2] WOLFRAM S.Computation Theory of Cellular Automata[J].Communications in Mathematical Physics，1984，96(1):15-57.

[3] JAMES P C，KARL Y.Inferring Statistical Complexity[J].Physical Review Letters，1989，63(2)：105-108.

[4] JAMES P C.The Calculi of Emergence：Computation，Dynamics，and Induction[J].Physica D，1994，75(1-3):11-54.

[5] CRAMER F.Chaos and Order：The Complex Structure of Living Systems[M].VCH，New York:VCH Publish,1993：340-345.

[6] SHINER J S，MATT D，LANDSBERG P T.Simple Measure for Complexity[J].Physical Review E，1999,59(145):1459-1464.

[7] 宋学峰.系统复杂性度量方法[J].系统工程理论与实践,2002，22(1)：10-14.

SONG Xue-feng.The Methods for Measuring the Complexity of Systems[J]. Systems Engineering-theory & Practice,2002,22(1):10-14.

[8] El-mezyani T，WiLSON R，SATTLER M，et al.Quantification of Complexity of Power Electronics Based Systems[J].IET Electrical Systems in Transportation,2012，2(4):211-222.

[9] AREEJIT P，MANOJ K，VITTAL P.Complexity Metrics for Manufacturing Control Architectures Based on Software and Information Flow[J].Computers & Industrial Engineering,2005,49(1):1-20.

[10] LUO Ai-min，HUANG Li.Entropy-based Complexity Analysis for Architecture of Information System[C]//Proceedings of 2008 IEEE International Conference on Networking Sensing and Control.New York：IEEE Press,2008:1734-1738.

[11] GAO Jian-bo，LIU Fei-yan，ZHANG Jian-fang，et al.Information Entropy as a Basic Building Block of Complexity Theory[J].Entropy,2013,15(9):3396-3418.

[12] FILIZ I.An Entropy-based Approach for Measuring Complexity in Supply Chains[J].International Journal of Production Research,2010,48(12):3681-3696.

[13] 金菊良，魏一鸣.复杂系统广义智能评价方法与应用[M].北京：科学出版社,2008:1-2.

[14] 戴汝为，沙飞.复杂性问题研究综述：概念及研究方法[J].自然杂志,1995,17(2):73-77.

DAI Ru-wei，SHA Fei.Review on Complexity Research：Concepts and Mythology[J].Chinese Journal of Nature,1995,17(2):73-77.

[15] 苗东升.钱学森复杂性研究评述[J].西安交通大学学报(社会科学版),2004，24(4)：67-71.

MIAO Dong-sheng.Review on the Study of Complexity by Qian Xue-sen[J].Journal of Xi’an Jiaotong University:Social Sciences,2004,24(4):67-71.

[16] 宁滨，唐涛，李开成，等.高速列车运行控制系统[M].北京：科学出版社,2012：3.

[17] 黄欣荣.复杂性科学的方法论研究[M].重庆：重庆大学出版社,2012：37.

[18] 何天祥.企业管理结构复杂度评价的新方法-熵正交投影法[J].系统工程理论与实践,2005,18(4)：115-119.

HE Tian-xiang.A New Method for Evaluating the Complexity of Enterprise Management Structure Entropy -Vector Projection[J].Systems Engineering-theory & Practice,2005,18(4):115-119.

[19] 铁道部科学技术司，铁道部运输局.科技运[2008]127号CTCS-3级列控系统系统需求规范[S].北京：中国铁道出版社，2008.