农安扶余地区油页岩测井识别与总含油率计算

翟艇, 潘保芝

(吉林大学地球探测科学与技术学院, 吉林 长春 130026)

0 引 言

农安扶余地区位于松辽盆地南部,该区域油页岩主要发育于白垩系青山口组一段、嫩江组一段和二段,且集中分布在各段底部[1]。油页岩均为湖相沉积,油页岩的产出层位往往与最大湖泛面一致,青山口组和嫩江组的油页岩中富含固体有机质,构成了松辽盆地主要生油岩系。油页岩具有高自然伽马(GR)、高电阻率(Rt)、高声波时差(AC)、低密度(DEN)的特性[2]。油页岩的这种特性决定了其与泥岩、砂岩的测井曲线有着明显的差异。在正常情况下,地层的有机质含量越高,其在测井曲线上的异常响应越明显。因此,油页岩的大多数识别方法以此为依据,借助单条或者多条测井曲线进行判别[3]。

目前对于油页岩含油率的评价主要借鉴烃源岩的评价方法,即首先根据Δ logR原理计算出油页岩中的有机碳含量。贺君玲等[1]通过统计分析得出含油率与有机碳含量间的线性关系,建立了松辽盆地嫩二段油页岩的测井资料与含油率间的定量统计关系式。当油页岩的成熟度较高,即在油页岩中生成的、呈分散状态的石油,当其数量超过残余油饱和度时,在岩石微小孔隙中就会存在游离态的油,因此近年来有学者提出利用油页岩导电方程计算游离态油的含油率[4]。此后有学者在此基础之上,对于成熟度较高的油页岩进一步提出了计算总含油率的概念,即将含油率分为2部分(即有机质在低温干馏后可以产生的含油率和孔隙中游离态的含油率)分别进行求取,最后二者相加之和即为油页岩的总含油率[5]。

本文以吉林省扶余伊家店A井以及农安哈拉海B井测井数据为基础,从岩性识别以及总含油率计算2个方面分别进行测井解释,提出利用曲线幅差法进行油页岩的岩性识别,并将其结果与双参数交会图法进行对比,从识别效果看,2种方法都能够达到准确识别油页岩的目的。对于A井的油页岩识别率分别为90.59%和51.18%,幅差法对于B井油页岩识别率为87.61%。针对2种不同意义下的含油率,通过拟合岩心数据与测井曲线之间的关系,建立简化的油页岩四组分体积模型,并借助油页岩导电方程对有机质在低温干馏后可以产生的含油率以及孔隙中游离态的含油率,进而求得总含油率。

1 松辽盆地南部油页岩测井响应特征

油页岩A井深402 m,录井资料显示250 m以上岩性主要为砂岩和泥岩,自然伽马在泥岩段表现为高值,部分砂岩碎屑由于含有较高的放射性物质而表现为较高幅值;在砂岩段表现为低声波时差、高电阻率。250 m以下主要为泥岩和油页岩,泥岩的自然伽马和电阻率曲线幅差与上部相比均有所下降,在350～380 m井段之间分布有一定厚度的油页岩层,对应自然伽马、声波时差以及电阻率测井曲线出现高值。

油页岩B井深706 m,自然伽马曲线除出现较薄但幅值很高的峰值以外,在绝大部分井段保持中等数值;电阻率多在50～230 Ω·m范围内。在240～300 m以及610～680 m井段之间分别分布有嫩江组以及青山口组油页岩层段。下部青山口组油页岩比上部嫩江组油页岩电阻率测井曲线幅值大很多;声波曲线在青山口组幅值较低,基本在200～280 μs/m之间,嫩江组多在300 μs/m以上。

2 利用曲线幅差法识别油页岩

根据油页岩“三高一低”的测井响应特征,在油页岩层段上,电阻率、声波以及自然伽马测井曲线会出现有别于围岩的明显高值,由此当将3条高值曲线中的任意2条进行反向刻度时,在2条曲线之间就会出现一定的幅度差,并且随着地层中有机质的含量升高,幅差值也随之增加,当增加到一定程度时,就指示该处地层为油页岩,因此,提出利用曲线幅差法进行油页岩的岩性识别。

2.1 基本原理

对A井50～380 m井段的GR以及Rt数据进行交会,根据油页岩、泥岩以及砂岩的岩性特征,在交会图(见图1)上找到3种岩性的位置:油页岩由于高伽马、高电阻率值而在交会图的右上方位置;泥岩的GR值低于油页岩而高于砂岩;砂岩的电阻率值低于油页岩而大于泥岩,据此分别找到砂岩及泥岩点的位置。3种岩性确定下来之后,根据砂岩点(60,83)、泥岩点(102,50)坐标连线确定出砂泥岩线方程

y=130-0.79x

(1)

式中,y为Rt值,Ω·m;x为GR值,API。

图1 曲线幅差法识别岩性原理图(油页岩A井50～380 m)

随着地层中有机质含量的逐渐增加,相应GR以及Rt值逐渐变大,岩性也逐渐由砂泥岩向着油页岩过渡,在图1上表现为数据点逐渐远离砂泥岩线并向着油页岩点靠近。计算不同数据点与砂泥岩线之间的距离d,在确定出油页岩GR、Rt的最小值(GRmin,Rt,min)之后,计算该点(104,66)距离砂泥岩线的距离dmin,并将其作为油页岩与砂泥岩岩性的分界线,规定凡是d大于或等于dmin的层段判定为油页岩。将横坐标GR的2个端点值(47、108)代入式(1),求取出相应纵坐标Rt的变化范围(93、2.7)。在解释图上,将GR、Rt这2条曲线按照上述求取出来的范围进行刻度(这里对Rt曲线进行反向刻度),在砂泥岩段曲线几乎重合或者出现小幅度的曲线差值,而在油页岩层段上,2条曲线将出现较大的幅度差。

2.2 应用效果分析

对于A井,根据录井岩性剖面,将典型岩性所对应厚层的测井曲线进行读数,制作交会图(见图2)。从图2可以看出,砂岩的电阻率较高,声波时差以及自然伽马值较低,泥岩的电阻率较低,声波时差以及自然伽马值较高,而油页岩地层的测井响应符合“三高”的特征,在交会图上能够与其他2种岩性明显的区别开来。从图2读出不同岩性参数的取值范围以此进行岩性识别。图3是2种方法对油页岩A井的处理效果对比图。

图2 油页岩A井GR-Rt交会图

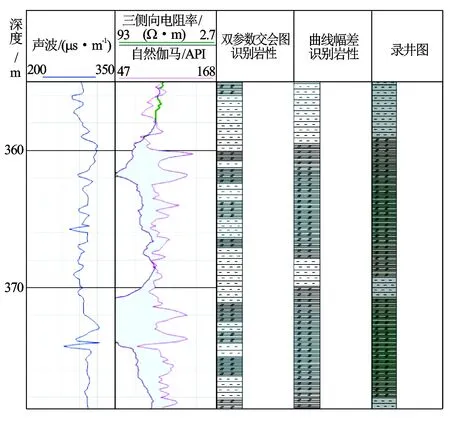
图3 伊家店油页岩A井(355～379 m)2种方法岩性识别解释图

从图3中可以看到,在GR-Rt曲线幅差较大的地方识别出来的油页岩与录井岩性有着很好的吻合度,油页岩识别率为90.59%;而双参数交会图法对于一定厚度的油页岩识别效果不佳,油页岩识别率为51.18%。利用幅差法又对油页岩B井进行了同样的处理,获得了解释图4。图4中,在200～240 m处2条曲线基本重叠在一起,识别结果为泥岩,与录井岩性吻合;240 m以下除了251～261 m这段录井显示为粉砂质泥岩外(泥岩中粉砂质成分较高导致GR值偏大),其他部位的油页岩也都被准确地识别出来,油页岩识别率为87.61%。

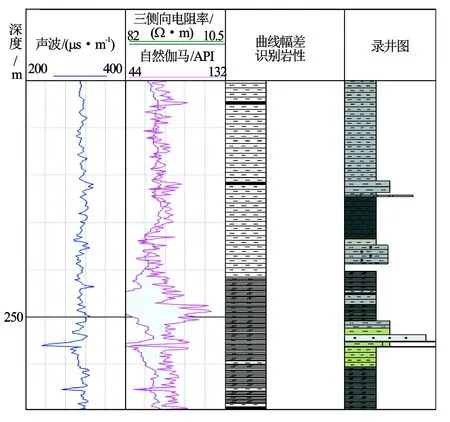
图4 农安油页岩B井(200～270 m)2种方法岩性识别解释图

3 油页岩总含油率的计算

将油页岩含油率的求取分为2部分,第1部分依据ΔlogR原理,即借助实验室分析出来的含油率、有机碳含量与已知测井数据进行拟合,建立起含油率与测井数据之间的线性关系式进而求取出Ta1;对于第2部分游离态含油率Ta2的求取,首先建立起骨架+泥质+有机质+孔隙的油页岩四组分体积模型,并在自然伽马、声波时差2条测井曲线基础之上提出间接求取四组分的方法。将求取出的相关体积分数及参数值输入到油页岩导电方程中,获得Ta2;最后将2部分含油率相加,即获得油页岩中总含油率Ta。

3.1 求取有机质低温干馏后的含油率Ta1

根据ΔlogR原理,TOC与logRt、AC、GR之间呈一定的线性关系,通过对岩心总有机碳含量(TOC)数据与对应的测井数据进行回归拟合可以得到如下关系

TOC=13.622 logRt+0.137AC+

0.018GR-63.49

(2)

拟合出来的TOC与岩心TOC相关性很高,对二者进行45 °检验,平均相对误差0.113。

对岩心Ta和TOC进行回归分析(见图5),得到二者之间的关系式

Ta1=0.729TOC+0.058

(3)

图5 油页岩A井岩心总有机碳含量与含油率交会图

将式(2)和式(3)进行合并,得到直接用测井曲线计算含油率的公式

Ta1=16.276 logRt+0.164AC+

0.022GR-78.767

(4)

3.2 求取孔隙中游离态的含油率Ta2

与一般页岩相比,油页岩除了具有骨架、孔隙流体以及泥质外,还含有大量的有机质。考虑到缺少相关测井数据无法实现对该模型的求解,因此进一步将模型简化为骨架+泥质+有机质+孔隙的油页岩四组分体积模型。在该地区没有进行密度测井,且相关组分电导率参数的确定存在一定困难,因此在已有声波时差、自然伽马测井曲线的基础之上提出间接求取四组分体积的方法。首先,将拟合的总有机碳质量百分含量转换成有机质的体积百分含量[6]

(5)

式中,VTOC为有机质体积百分含量,%;ρ为地层密度,g/cm3,由于没有密度测井曲线,计算时,将实验室测量岩心体密度值取平均作为地层密度,即ρ=2.2 g/cm3;ρTOC为有机质密度,一般取1.1 g/cm3[7],KCH为有机碳转化系数,与成岩作用以及有机质类型有关,近似认为转化已完全,即KCH=1。根据VTOC值去掉原地层中有机质的影响,并建立起除有机质之外其他3个组分的体积模型

(6)

式中,Vma、Vsh、φ分别为骨架、泥质以及孔隙的体积百分含量,%;GRTOC、GRma、GRsh、GRf分别为有机质、骨架、泥质、孔隙的自然伽马值,API;ACTOC、ACma、ACsh、ACf分别为有机质、骨架、泥质、孔隙的声波时差值,μs/m。泥质的相关参数通过对泥岩段测井数据进行交会得到,有机质的参数经过查阅文献获得[7],表1列出了相关参数的取值。

表1 各个组分的参数取值

将确定好的参数输入到相关求取体积分数的程序中进行求解,得到Vma、Vsh、φ值。将Vsh、φ以及其他参数带入到油页岩导电方程(7)中[4],就可以得到孔隙中游离态油的含油率

(7)

3.3 应用效果分析

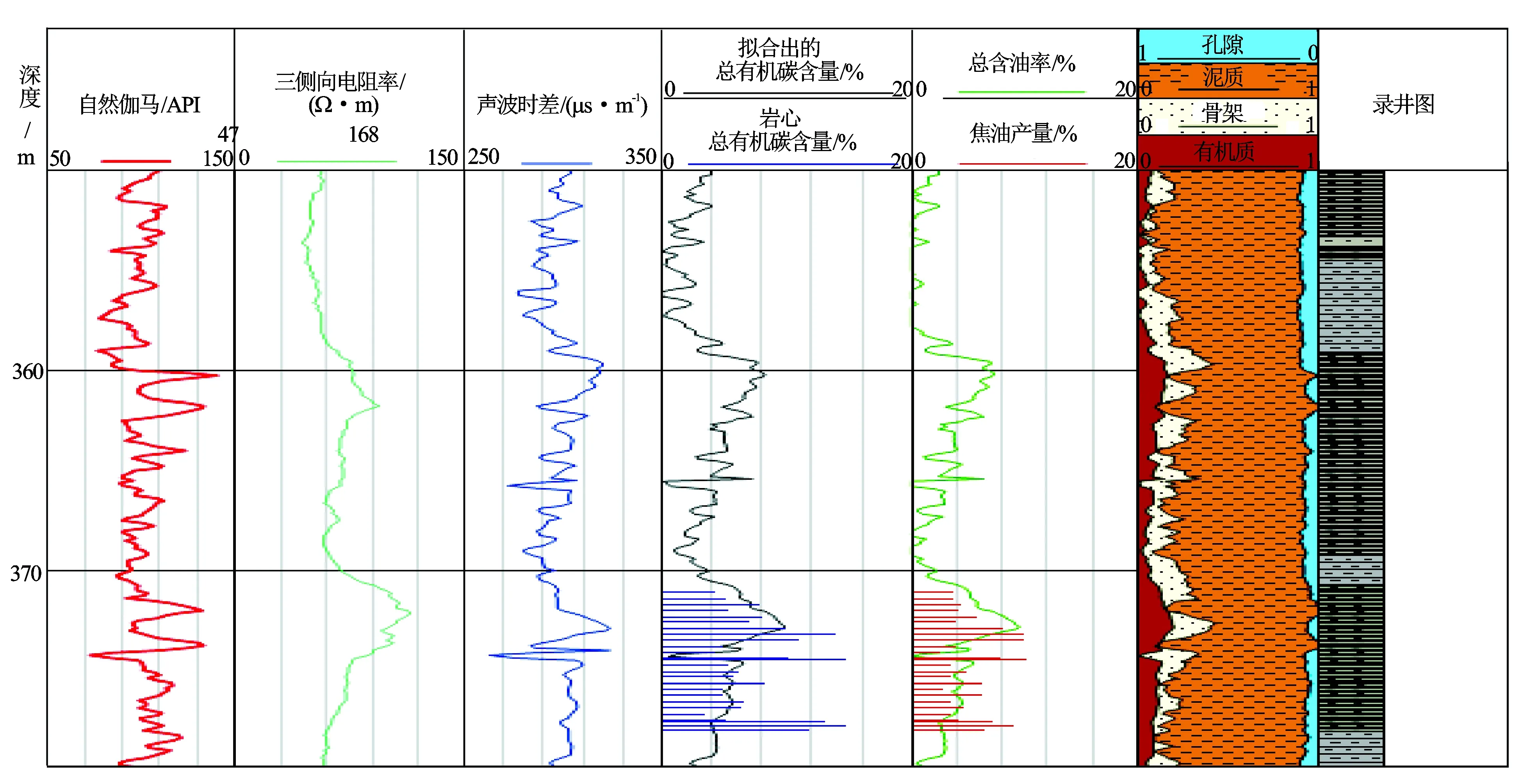
图6 油页岩A井(350～380 m)综合解释图

图7 油页岩B井(610～690 m)综合解释图

将确定的2种含油率相加,即可得到油页岩总的含油率,即Ta=Ta1+Ta2;再将计算出来的总含油率与岩心含油率进行对比,得到A井350～380 m段的综合解释图(见图6)。 从图6可以看到,计算出来的含油率与大部分岩心数据都能够吻合得很好,只是在局部岩心值很高的层段计算值偏低。对计算结果进行45 °检验,计算含油率与岩心数据吻合程度较高,平均相对误差0.245。

用相同的方法对油页岩B井的含油率进行了计算。需要注意的是,B井由于没有岩心TOC数据,求解Ta1时,直接对岩心Ta数据与测井数据进行拟合,求解TOC时借助A井TOC的拟合关系式。图7是油页岩B井610～690 m段的综合解释图。从图7中可以看到,计算出来的含油率曲线起伏趋势与岩心数据吻合程度高,与A井相似,在局部岩心含油率很高的点处,计算值偏低。对计算结果进行45 °检验,计算结果平均相对误差0.279。

4 结 论

(1) 通过对测井曲线进行分析,农安扶余地区2口井的油页岩符合“三高”的测井曲线特征。

(2) 在油页岩测井响应特征的基础之上,提出利用曲线幅差法对2口油页岩井进行岩性识别,识别效果显示该方法能够达到准确识别油页岩的目的,对于A、B井的油页岩识别率分别为90.59%和87.61%。该方法关键在于确定出砂泥岩线方程,保证在砂泥岩段曲线重叠或幅差较小,但是当砂泥岩中放射性矿物含量较高或是其他原因造成曲线出现高值时,会造成识别结果的一定误差。

(3) 将油页岩体积模型进一步简化为骨架+泥质+有机质+孔隙的四组分体积模型,在现有测井数据的基础之上提出间接求取四组分的方法。

(4) 充分考虑到油页岩中2种不同意义下的含油率,提出将总含油率Ta分成Ta1和Ta2分别进行求取。分别建立A、B井岩心数据与测井曲线之间的拟合关系,其中A井岩心Ta与TOC值之间具有很强的相关性。从A、B井计算解释图来看,总含油率的计算方法能够在一定程度上准确地计算出油页岩的含油率,计算出的含油率与岩心含油率之间的平均相对误差分别为0.245和0.279。值得注意的是,在岩心Ta值很高的某些局部深度上,计算结果值稍低,这可能是由于相关参数的确定存在一定的误差所造成的。

参考文献:

[1] 贺君玲, 邓守伟, 陈文龙, 等. 利用测井技术评价松辽盆地南部油页岩 [J]. 吉林大学学报: 地球科学版, 2006, 36(6): 909-914.

[2] 陆巧焕, 张晋言, 李绍霞. 测井资料在生油岩评价中的应用 [J]. 测井技术, 2006, 30(1): 80-83.

[3] 朱建伟, 赵刚, 刘博, 等. 油页岩测井识别技术及应用 [J]. 吉林大学学报: 地球科学版, 2012, 42(2): 289-295.

[4] 王翠平, 潘保芝, 林鹤, 等. 油页岩含油率的测井评价方法 [J]. 测井技术, 2011, 35(6): 564-567.

[5] 翟艇, 潘保芝, 王翠平. 油页岩总含油率的测井评价方法 [J]. 国外测井技术, 2012(6): 68-70.

[6] 张晋言. 页岩油测井评价方法及其应用 [J]. 地球物理学进展, 2012, 27(3): 1154-1162.

[7] 史冀忠. 内蒙古巴格毛德油页岩特征及测井响应研究 [D]. 长春: 吉林大学, 2008.