井间电磁成像测井数值模式匹配算法

臧德福, 姬勇力, 李智强, 晁永胜, 杨爱锋

(1.中石化胜利石油工程有限公司测井公司, 山东 东营 257096;2.中国电子科技集团公司第22研究所, 河南 新乡 453003)

0 引 言

井间电磁成像技术主要用来对井间的电导率分布进行成像。与电测井相比,它具有更大的探测范围;与大地电磁及地面-井电磁法相比,它具有更高的精度[1]。利用该方法可进一步求取孔隙度、流体饱和度分布和渗透率分布信息,从而发现漏失的油气层,监测油气水的运移情况,确定最佳的布井位置,提高采收率。

20世纪80年代以来,美国加州大学伯克利分校的研究人员对井间电磁成像技术进行了大量的理论和实验研究[2-6],并取得了重要进展,包括井间电磁系统的灵敏度分析和适用范围、井间电磁方法的分辨率、仪器装备研究、金属套管的影响、井间电磁成像方法。自1997年胜利油田、中国石油大学(华东)与美国的EMI(Electromagnetic Instruments Inc.)公司合作,开展井间电磁成像系统的应用研究,并在胜利油田进行了3对井的测量试验。3次试验都采集到可靠的井间电磁数据,利用这些数据进行轴对称二维近似反演得到的井间电导率成像图在分析井间油气分布、砂体展布等方面见到较好的效果,充分证明井间电磁成像技术是油藏研究中具有开创性的重要技术手段[7-8]。近年来,胜利测井公司又开展了更远距离、更高性能的井间电磁成像技术的研究[9]。

计算井间电磁场的正演方法包括微分方程法和积分方程法2类。求解微分方程可采用有限元法和有限差分法,其求解范围是整个井间区域,经离散后形成含大型稀疏矩阵的线性方程组,适用于复杂井间地层模型。由于井间电磁场的求解区域要比单井电磁场大得多,导致计算量巨大,只有超级计算机才能完成。积分方程的求解范围只是井间电导率异常区域,因而与微分方程相比求解区域要小得多,适用于简单的井间地层模型。积分方程法更适合于反演过程中的正演计算,因为其计算量相对较小,且成像区域可选为有限区域。但是,积分方程经离散后形成含致密矩阵的线性方程组,若在计算时存储整个矩阵,则所需内存量很大,计算速度将变慢,从而降低计算效率。上述2种方法计算效率都不高,因此,开发出高效的井间电磁成像的正演模拟方法是该领域的一项重要研究内容[10]。

Padensi等[11-12]在研究电磁散射时,把波膜的概念与有限元结合起来,提出一种称为数值模式匹配(NMM)的半解析、半有限元解法。该方法把二维数值问题转化为一维解析解和一维数值解的结合,大大减少了计算量。Chew等[13-14]把该方法应用到普通电阻率测井中,其效率是有限元的数百倍。张庚骥等[15-16]用NMM法研究了轴对称条件下纵向成层、径向不均匀的地层模型中普通电阻率测井的响应,在纵向上采用解析方法推导了反射矩阵和透射矩阵的递推公式,在径向上采用数值解时改进了基函数(幅度基函数和斜度基函数),其结果不仅达到了有限元方法的精度,而且大大提高了运算速度。仵杰等[17]针对NMM算法在复杂测井情况下的误差详细分析了基函数类型、个数以及径向网格的剖分边界位置,提出了相应的改进措施。本文在上述基础上,将NMM法用于井间电磁成像正演计算,结合井间电磁成像数据测量的特点,利用并行计算快速计算出所有数据。

1 井间电磁成像中的NMM法

1.1 地层模型和NMM法原理

井间电磁成像是在2口井中分别放入发射与接收装置,通过测量不同深度的磁场响应反演2口井之间剖面的电导率分布(见图1)。

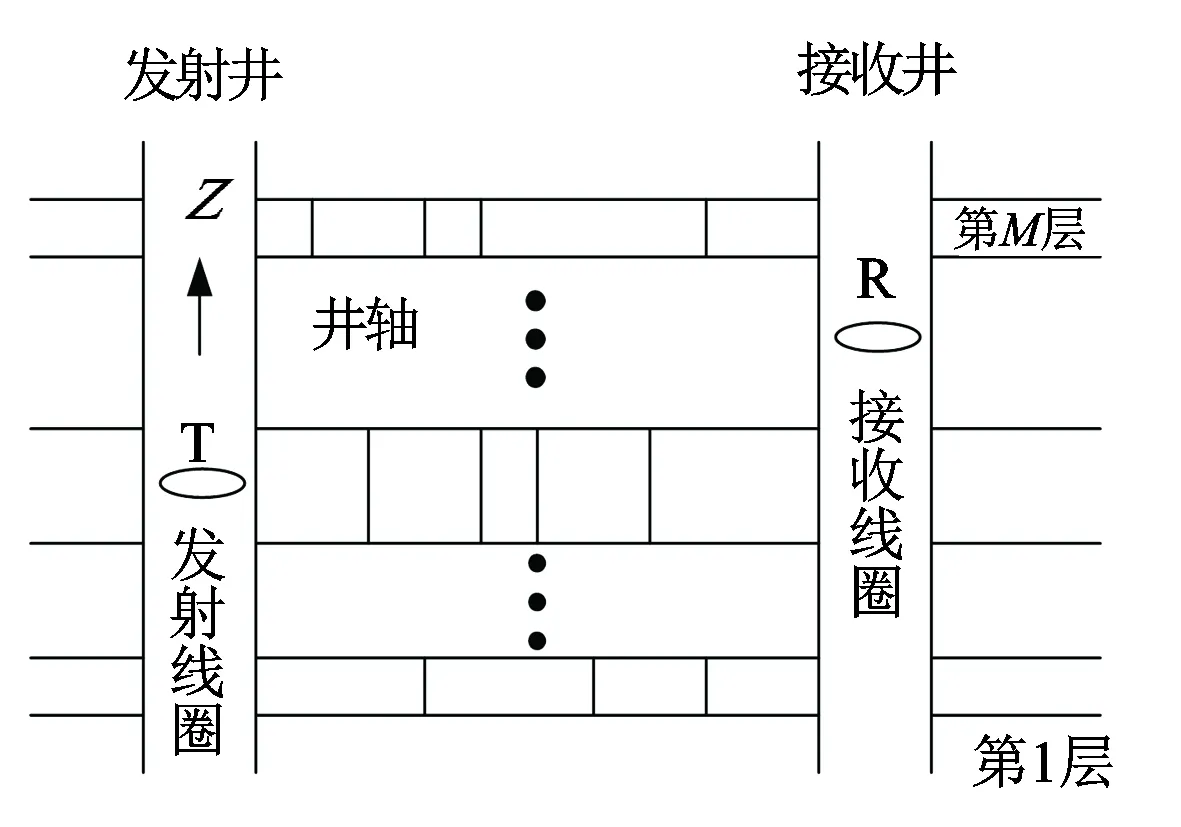
图1 井间电磁成像地层模型

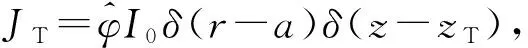
(1)

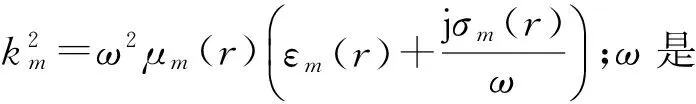
在无发射源时,式(1)等式右边为0,即

(2)

其边界条件为

1.2 NMM法基本原理

采用分离变量法对式(2)求解[15-16],令

(3)

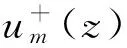
而fm(r)没有解析解,只能用数值解求解。fm(r)近似表示为

(4)

式中,Cm是本征向量cm组成的矩阵。式(4)等价于式(5)矩阵形式的本征值方程

(5)

1.3 NMM法计算步骤

(1) 建立地层模型。

(2) 选取基函数,形成矩阵Am、B。

(3) 求解广义特征值问题,得到Cm。

(4) 确定发射源所在位置。

(7) 确定接收线圈的位置,代入式(3)即可求出接收线圈处的电场强度。

2 井间电磁成像中NMM法的应用

2.1 重构NMM法计算步骤

从上面的推导可知,NMM法是1个发射点计算1个接收场强,井间电磁成像系统为确保成像效果,需尽可能多地采集数据。通常做法是接收线圈固定在某深度,发射线圈在整个测量深度区间和移动以固定间距采集数据,然后变换接收线圈深度,重复测量。例如井间距500 m,深度区间200 m,每2 m采集1个点,则共需采集10 000个点,逐个计算场强会导致一次正演所用时间非常长。分析NMM法的计算原理与井间电磁成像的测量方式,可知当地质模型建立以后,正演中含有大量重复计算,可以省略,这样大大缩短正演时间。

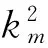
(2) 地层划分要足够细,反演成像分辨率才高,Cm与Λm基本上每层模型都要用到,可以将2个参数在第1次计算时存储下来,在后面的每个发射-接收点直接调用。只要地层电导率模型不变,Cm与Λm也不变。

(3) 每个接收点都对应相同数量的发射点位置,可以将仅与发射点相关的公式全部计算出来,这样就避免了每个接收点都重复计算。

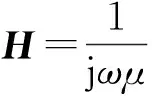
从上述计算步骤中可以看出,在前3步中可提前计算出固定值用于后续计算,这样节省大量运算时间,而且其所占存储空间相对于有限元与有限差分也非常小,普通计算机完全可以满足需求。

2.2 数值模式匹配的并行计算

从20世纪60年代起,人们就开始探索数值计算方法的并行化技术和计算结构的并行化设计方法,解决单核计算机难以完成的工程与科学技术领域内规模巨大、实现要求严格的数值计算问题。并行计算就是把一个需要非常巨大的计算能力才能解决的问题分成许多小问题,把这些小问题分配给不同计算机或处理器进行并行处理,将计算结果综合得到最终的结果。为加快运算速度和解决大容量存储的求解问题,并行编程需要具有多个内部处理器的单计算机或者多个互联的计算机[18]。以1999年NVIDIA公司提出GPU概念为分界点,之前的并行计算都是基于多CPU并行处理,之后的并行计算向着多核CPU与GPU异构协同的方向发展。CPU并行与GPU并行的区别在于单个GPU的多核心,重复计算能力强,通过低投入的GPU计算阵列就可以达到以往大型CPU阵列并行系统的效率。但是GPU的每个处理核心在执行指令的时候控制优化少,速度不够高,近些年出现的多核CPU其核心最多也就16核,并行度不高,因此未来的发展方向是CPU/GPU异构协同发展[19]。

GPU并行大多用于超级计算机,考虑到井间电磁成像系统数据处理的实际情况以及便携性与经济性,采用多核CPU并行基本可以满足需要,而当前无论是台式机还是便携机,都具有多核CPU,若采用并行计算将多核CPU充分利用,则重构NMM法的计算速度可以大幅提高。图2是重构NMM法的并行处理流程图。

图2 NMM法在井间电磁成像正演中流程图

2.3 模拟仿真

2.3.1 均匀地层对比验证

通过与均匀地层的解析解对比,验证NMM法的精确度。设均匀介质中有一半径为aT、匝数为NT的发射线圈,其中通过交变电流IT=I0ej ω t。它在空间形成的交变电场与磁场也随时间按照正弦规律变化。将坐标原点选在线圈中心,z轴垂直于线圈平面,在轴对称的柱坐标系(r,φ,z)中,有

(6)

建立地质模型,纵向100层,径向300层,网格间距2 m×2 m,地层电导率为1 S/m,幅度和斜度基函数分别取52点。图3为10 Hz频率下,随井间距变化的误差示意图。NMM算法在频率选取原则范围内的精度完全满足系统需求[7]。

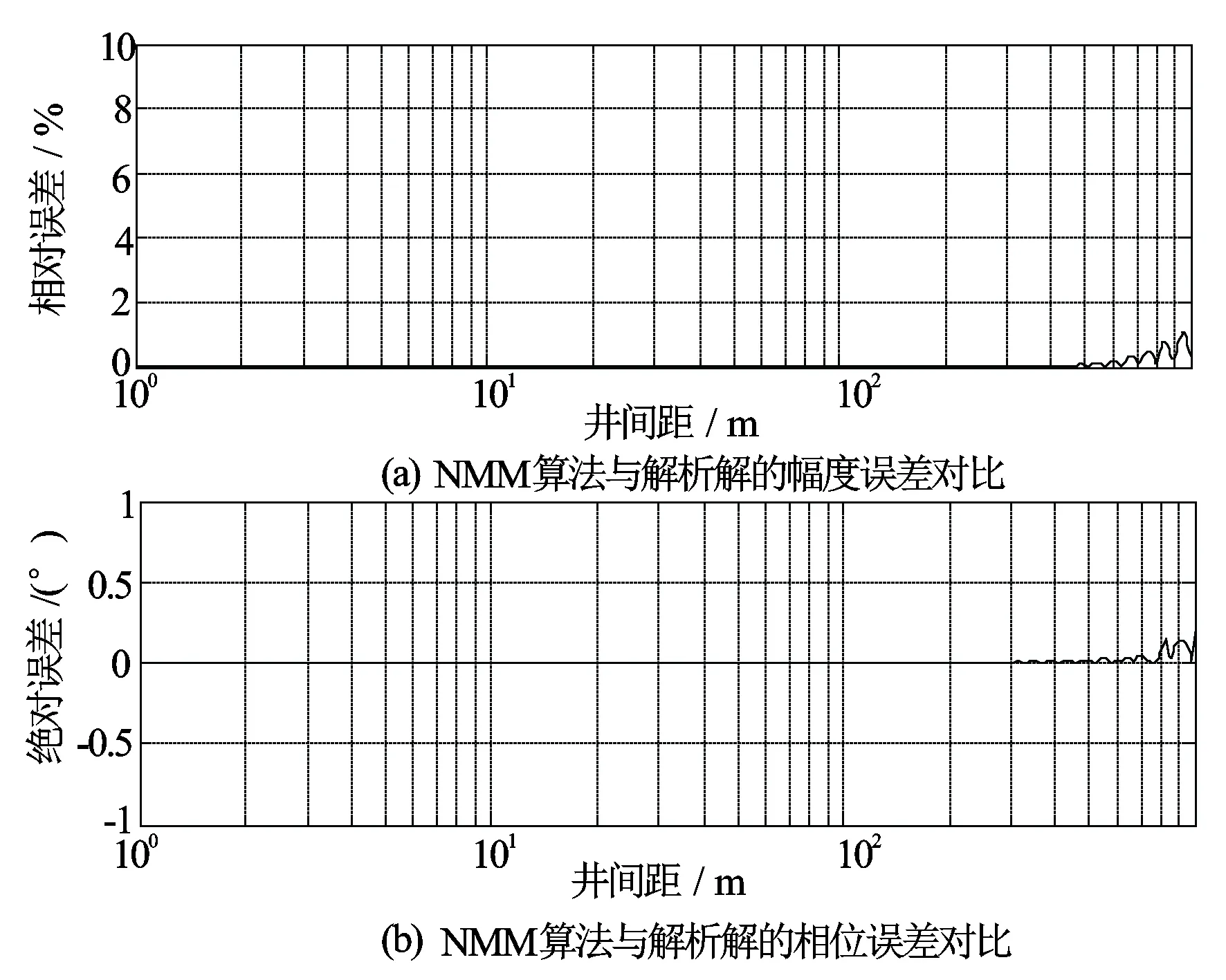
图3 NMM法与解析解误差随井间距变化关系

为了说明本文算法的优势,在四核便携式计算机(主频2.5 GHz)上采用原NMM法及结合井间电磁测量的NMM法、并行NMM法计算,对其运算时间进行对比,在XP双核(主频2.5 GHz)和win7 四核系统的台式机(主频3.3 GHz)进行并行运算对比。图4是运算耗费时间示意图,从图4中可知,原NMM方法一个点需要36 s,而且多个点重复调用单点计算程序,其所用时间与计算点数成线性正比关系。结合井间电磁成像工作原理改进后的NMM法单点计算只需10 s,随着计算点数的增加,优化后的NMM法计算速度优势越来越明显,对于1万点计算,原方法需100 h,而优化后的方法只需12 min。当采用双核并行时,仅需7 min,若在主频更高计算机上进行4核并行计算,只需2.5 min,可以大大提高NMM法反演成像的效率。

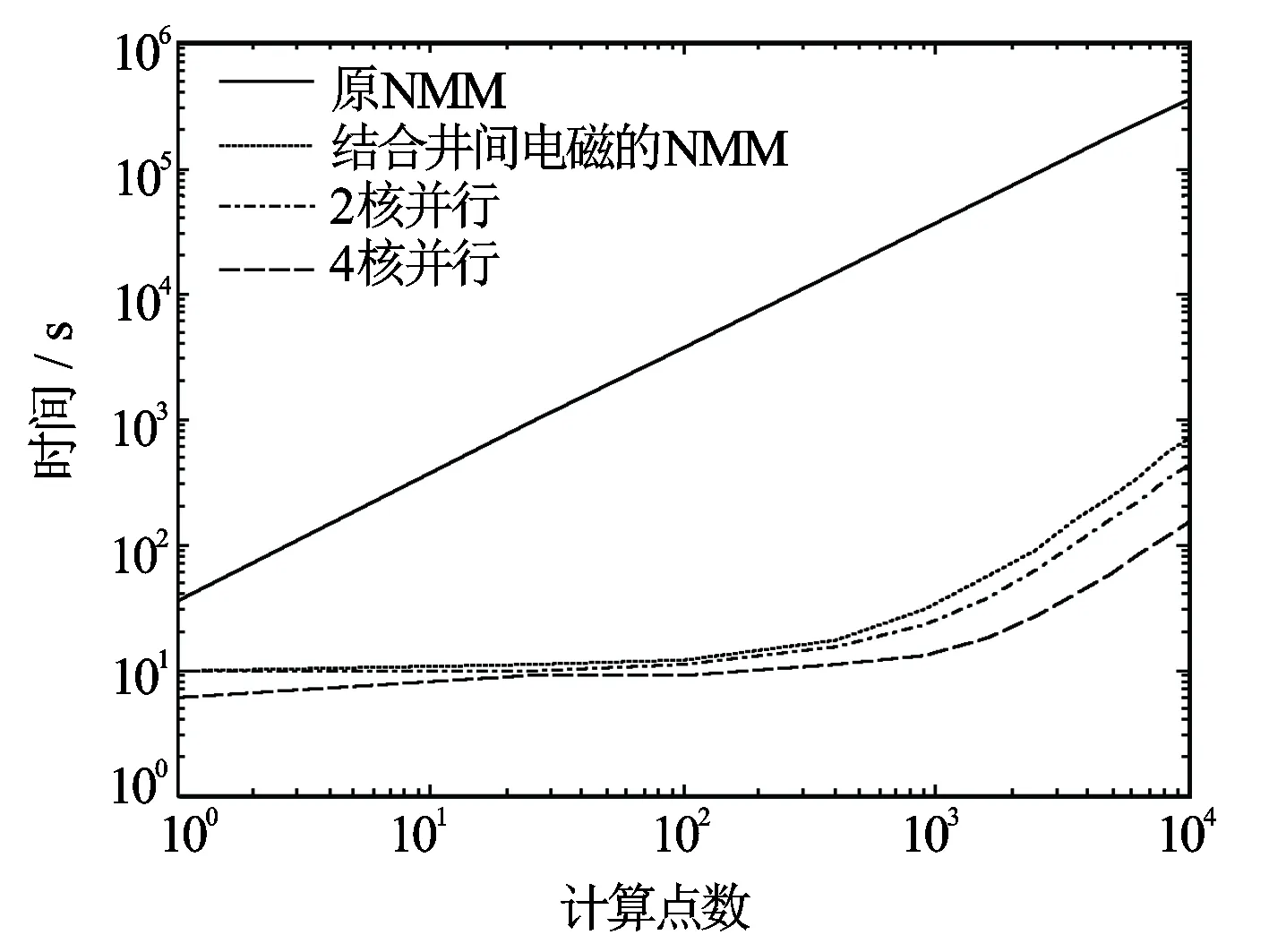
图4 NMM法计算速度对比

2.3.2 纵向成层一维井间地层模型

通过与均匀地层的对比证明了该方法的正确性以及高效率,然而均匀地质模型很难见到,因此,为进一步证明该方法的有效,按表1建立纵向成层一维井间模型,该模型有解析解[20]。地层共3层,边界分别为0、50 m和100 m,每层电导率见表1。模型边界以外电导率设为1 S/m,设频率为10 Hz,计算接收场强随井间距变化的误差(见图5)。计算结果表明,对于纵向成层一维井间地层,NMM算法的计算误差也非常小。

表1 水平成层一维井间地层电阻率

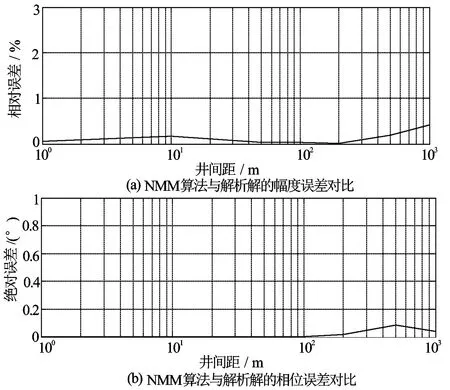
图5 NMM法计算速度对比

2.3.3 二维轴对称地层模型

目前,井间电磁三维成像难度太大,不易实现。对井间电磁进行二维或2.5维成像是研究最为广泛且成果最多的,魏宝君等[1]利用积分方程法针对轴对称二维非均匀地层的井间电磁成像问题做了大量的正演、反演工作。本文利用NMM与积分方程法在相同轴对称二维非均匀模型下开展正演计算,比较两者的计算精度以验证NMM方法用于井间电磁成像的可行性。

图6 轴对称二维非均匀地层模型

首先建立轴对称二维非均匀地质模型(见图6),数值代表电导率(单位S/m)。地层分10层,每层厚度为10 m,径向500 m,纵向为300～400 m,即测量深度范围为100 m。第1层起始边界300 m,第2层起始边界310 m,以此类推,第10层起始边界390 m。发射井以及模型边界外的电导率设为1 S/m。不考虑接收井,只需计算接收线圈在距发射线圈径向50、100、300、500 m的磁场强度。以发射线圈中心为径向零点,发射井半径为0.101 6 m,其他各区块对应边界如表2所示。发射点、接收点均为深度350 m处,频率为10 Hz时,计算磁场强度随井间距变化的结果,利用积分方程法(IE)、有限元法(FEM)与NMM这3种方法分别计算,其结果如图7所示。从图7可知,3种方法的计算结果基本一致,且NMM与FEM方法随着井间距的增加,其精度要高于IE方法。

表2 水平成层一维井间地层电阻率

图7 NMM与积分方程法、有限元法井间电磁成像正演计算结果对比

3 结 论

(1) NMM法可在常规配置的计算机上进行较大数据量的处理,适用于井间电磁成像这些复杂的正演数据处理。

(2) 结合井间电磁成像系统工作原理,通过重构获得改进NMM法。在改进NMM法的基础上采用并行优化技术,最终获得并行NMM法。

(3) 通过与均匀地层、水平成层一维地层解析解对比,以及与轴对称非均匀地层积分方程法、有限元法对比,验证了改进并行NMM法应用于大范围的井间电磁成像正演计算是可行的,而且效率更高。

参考文献:

[1] 魏宝君, 张庚骥, 曾文冲. 井间电磁成像的迭代反演算法 [J]. 地球物理学报, 1999, 42(5): 711-719.

[2] Wm R Petrick. Three Dimensional Resistivity Inversion Using Alpha Centers [J]. Geophysics, 1981, 46(8): 1148-1162.

[3] Tripp A C. Two-dimensional Resistivity Inversion [J]. Geophysics, 1984, 49(10): 1708-1717.

[4] Zhang Z, Zhou Z. Real-time Quasi-2-D Inversion of Array Resistivity Logging Data Neural Networks [J]. Geophysics, 2002, 67(2): 517-524.

[5] Xiong Zong-hou. Electromagnetic Modeling of 3-D Structures the Method of System Iteration Using Integal Equations [J]. Geophysics, 1992, 57(12): 1556-1561.

[6] Wannamaker P E, Hohmann G W, Sanlilipo WA. Electromagnetic Modeling of Three-dimensional Bodies in Layered Earths Using Integral Equations [J]. Geophysics, 1984, 49(1): 60-74.

[7] 曾文冲, 赵文杰, 臧德福. 井间电磁成像系统应用研究 [J]. 地球物理学报, 2001, 44(3): 411-420.

[8] 郭红旗, 臧德福, 王群力, 等. XBH2000井间电磁成像测井系统 [J]. 石油仪器, 2002, 16(3): 25-27.

[9] 臧德福, 郭红旗, 晁永胜, 等. 井间电磁成像测井系统分析与研究 [J]. 测井技术, 2013, 37(2): 177-182.

[10] 栗建军. 井间电磁测井原理、方法及套管对井间电磁测井影响规律的研究 [D]. 青岛: 中国海洋大学, 2004.

[11] Padensi M A, Ferreira L G. Method to Calculate the Reflection and Transmission of Guided Waves [J]. J. Opt. Soc. An. , 1982, 72(1): 126-130.

[12] Chew W C, et al. Diffraction of Waves by Discontinuities in Open Cylindrical Structures [M]. Houston: Proc. Internet. Symp. Institute of Elect. and Electron. Eng. Antennas and Propagation, 1983: 503-506.

[13] Chew W C, Barone S, Anderson B, et al. Diffrection of Axisymmetric Waves in a Borehole by Bed Boundary Discontinuities [J]. Geophysics, 1984, 49(24): 1586-1595.

[14] 聂在平, Chew W C, Liu Q H. 电磁波对轴对称二维层状介质的散射 [J]. 地球物理学报, 1992, 35(4): 479-489.

[15] 张庚骥, 汪涵明, 汪功礼. 成层介质中交流电测井响应 [J]. 地球物理学报, 1995, 38(6): 840-849.

[16] 张庚骥, 汪涵明. 普通电阻率测井的数值模式匹配算法 [J]. 石油大学学报: 自然科学版, 1996, 20(2): 23-29.

[17] 仵杰. 感应测井中的NMM法及其在咸水泥浆井中应用 [J]. 国外测井技术, 2011(1): 15-19.

[18] 李鹏, 邵明刚. 并行计算技术 [J]. 中国科技信息, 2006(7): 24-25.

[19] 卢风顺, 宋君强, 银福康, 等. CPU/GPU协同并行计算研究综述 [J]. 计算机科学, 2011, 38(3): 5-9.

[20] 田子立, 孙以睿, 刘桂兰. 感应测井理论及其应用 [M]. 北京: 石油工业出版社, 1984.