管道内脉冲式热源参数对流动传热的影响研究

刘彦昌, 刘得军, 刘兴斌, 王延军,3, 宋晓毓, 杨爱东

(1.中国石油大学(北京)地球物理与信息工程学院, 北京 102249; 2.大庆油田有限责任公司测试技术服务分公司, 黑龙江 大庆 163412; 3.哈尔滨工业大学电气工程及自动化学院, 黑龙江 哈尔滨 150001; 4.中国石油渤海钻探工程公司测井分公司, 天津 大港 300457)

0 引 言

有内部热源的流动与传热问题受到了国内外学者的重视和研究,这些研究多针对封闭空间[1-4],对开口水平管道内脉冲式热源的耦合传热情况的研究较少。热示踪流量测量仪器依靠内部热源产生热脉冲,热源的电气和几何参数对测量精度影响很大。传统热源参数设计根据实验数据,受实验条件限制,研究的情况和类型较少。本文依托生产测井中外径为54 mm的组合类仪器,考虑到井下高压环境,研究内径为37 mm的水平管道内放置不同参数的脉冲式热源进行流固耦合的热传导数值模拟研究,为优化热示踪流量仪器中的热源参数提供参考[5-6]。

1 理论基础

根据流体流动三大定律可以推导出流体力学的质量守恒方程、动量守恒方程和能量守恒方程[7-13]基本方程组。

1.1 质量守恒方程

质量守恒定律是单位时间内流体微元体中质量的增加,与同一时间间隔内流入该微元体的净质量相等。根据这一定律,可以得到质量守恒方程

(1)

式中,ρ为密度;t为时间;u为流体速度矢量。

1.2 动量守恒方程

动量守恒定律是指微元体中流体的动量对时间的变化率等于外界作用在该微元体上的各种力之和。根据动量守恒定律得到动量守恒方程

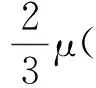
(2)

式中,μ为动力黏度系数;p为流体微元体上的压力;F为微元体上的体力,这里体积力只有重力;I为沿重力方向的单位向量。

1.3 能量守恒方程

Qvh+Wp

(3)

式中,T为流体温度;Cp为等压比热系数;k为导热系数;Q为源项;Qvh为性耗散项;Wp为压力项。

1.4 边界条件

出口边界条件[15]为自由出口,出口压力为大气压,压力为0。黏性力远小于惯性力,即无黏滞应力。可从动量守恒定律推出黏滞应力为0的公式

{μ[u+(u)T]}·n=0

(4)

式中,n为流体界面的外法向。

1.5 壁面条件

壁面是约束流体或固体的流动区域。模型采用无滑移的壁面条件

u=0

(5)

1.6 有限元方法

软件为有限元多物理场耦合分析软件COMSOL Multiphysics,采用有限元方法。有限元法(Fininte Element Methed,FEM)是将连续的求解域离散为一个单元组合体,用在每个单元内假设的近似函数来分片表示求解域上待求的未知场函数,近似函数通常由未知场函数及其导数在单元各节点的数值插值函数表达,使一个连续的无限自由度问题变成离散的有限自由度问题[8,14]。

2 建模及网格划分

2.1 模型建立

为了对水平管内不同热源几何形状、尺寸、截面安装位置及加热功率进行模拟,建立三维模型。热源材料设置为铜,密度为8 700 kg/m3,导热系数为400 W/(m·K),常压热容385 J/(kg·℃),流体为纯水,初始温度为300 K,设为不可压缩的牛顿型流体,流道和热源的几何模型和尺寸见图1。

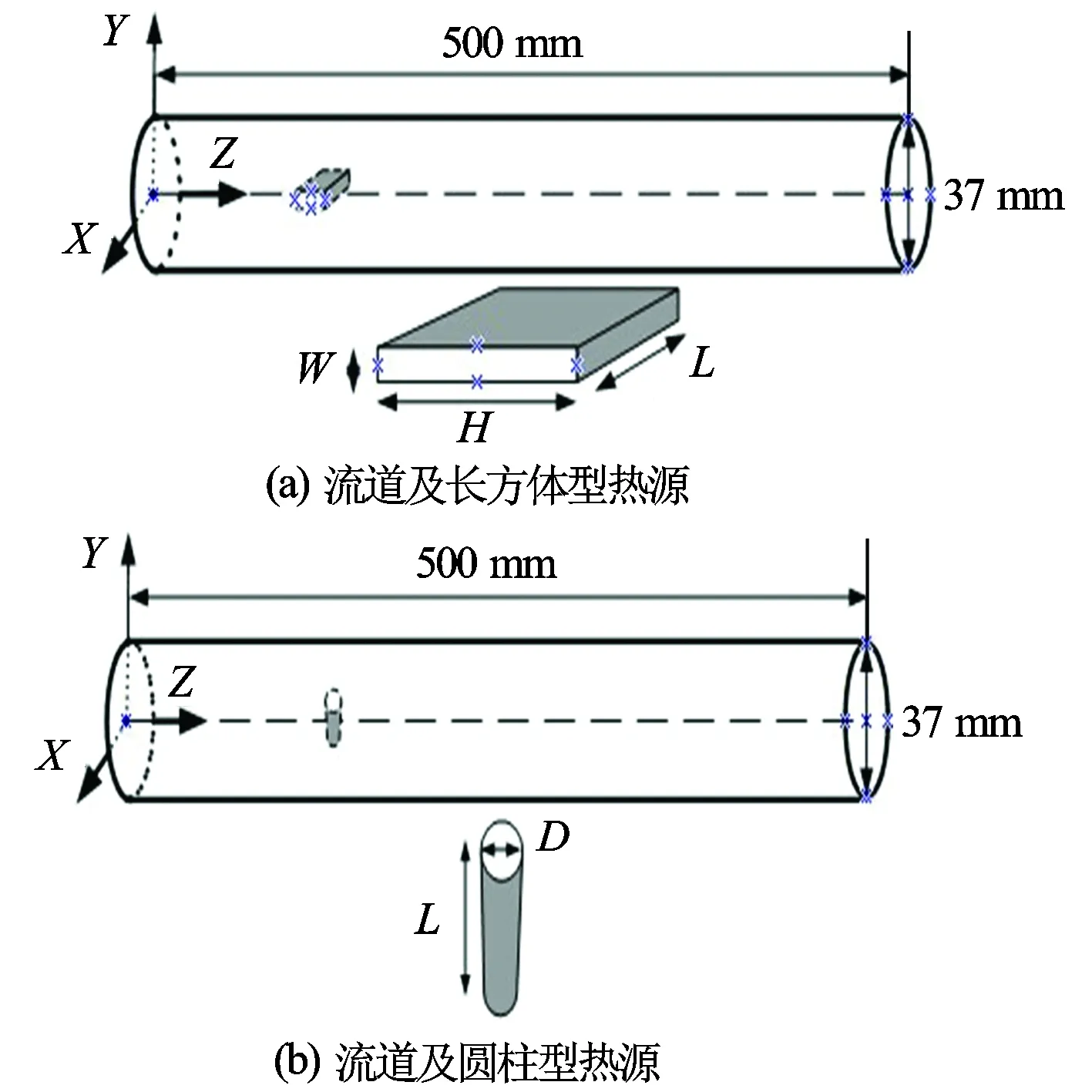
图1 流道及热源的三维几何模型

2.2 模型网格划分

建立的3D模型采用自由剖分四面体网格。流道极端粗化划分,热源较细化划分,共划分了11 922个网格。划分结果见图2。

图2 三维模型网格划分

3 数值模拟结果分析

3.1 不同形状的热源模拟结果分析

考虑到仪器在机械加工过程和安装时的方便性,设置热源的几何形状分别为长方体型和圆柱型[9],研究在同一加热功率(500 W)、脉冲加热时间(1 s)、换热系数下入口流量分别为1、5、10、15 m3/d流道内流体瞬间加热后温升变化情况。长方体型热源尺寸为高0.005 m、宽0.002 m、长0.004 m;圆柱形尺寸为半径0.002 m、长0.004 m。通过计算,2种类型热源换热面积相同,具有相同的换热系数。流体初始温度300 K,热源设置在管道中心处0.04 m处,通过数值模拟得到沿管道中心0.1 m处的温升曲线。

图3的温升曲线图中,在同一内热源作用下,不同流量温升的幅度大小不同,随着流量的增大,温升幅度会降低,长方体型热源最大温升值明显高于圆柱型热源,有利于对热脉冲信号的采集,在实际应用中应采用长方体型热源。

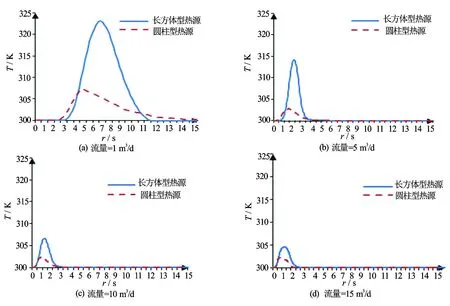
图3 不同流量下流体在Z=0.1 m处的温度变化曲线图

3.2 不同长度长方体型热源模拟结果分析

对于长方体型热源,为了降低对流道内流型的影响和获得更窄的热脉冲信号,长方体型热源的高度和宽度参数不宜设置太大,设置为高0.005 m、宽0.002 m,研究固定高度和宽度,长度分别为0.004、0.008、0.012、0.016、0.02 m,在同一加热功率(500 W)、同一脉冲加热时间(1 s),入口流量分别为1、5、10、15 m3/d流道内流体瞬间加热后温升变化情况。流体初始温度300 K,热源设置在流道中心0.04 m处,通过数值模拟得到沿管道中心0.1 m处的温升值。

从表1和图4可以看出,对于长方体型热源的宽和高不变的情况下改变长度,热源长度越大,沿管道中心0.1 m处的最大温升值越小。图5中,长方体的长度和0.1 m处的最大温升值基本呈线性关系,且随着流量增大斜率的绝对值减小,即当流量达到15 m3/d时几乎不受长方体型热源的长度的影响;在低流量时还需考虑深度对温升值的影响。

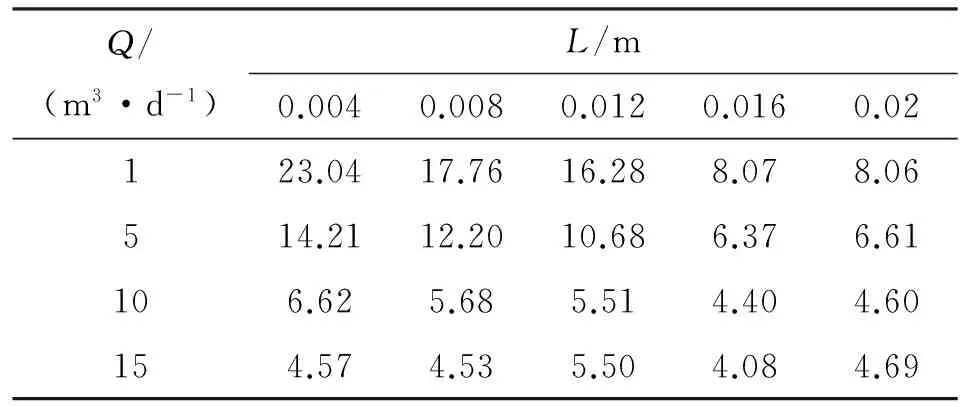
表1 不同流量下不同长度的长方体型热源在Z=0.1 m处的最大温升值(K)

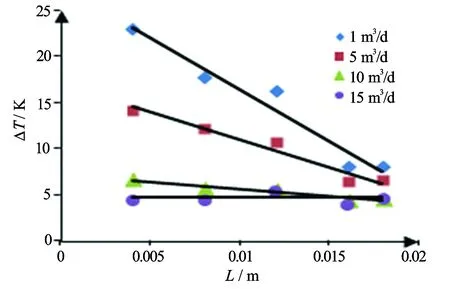
图4 不同流量下热源长度与最大温升的关系曲线图

3.3 不同功率的长方体型热源模拟结果分析

热示踪类测量仪器热源供电功率比较大,不能通过测井电缆的缆芯供电实现,需要单独配置井下电源。热源的功率越大[10],加热后流体的温升幅度就会越高;同时,需要配备的井下电源体积也会越大。为了优化井下电源设计,研究在同一流量下(1 m3/d)固定尺寸的长方体型热源(长0.004 mm、宽0.002 mm、高0.005 mm),在功率分别为100、200、300、400、500、600、700和800 W分析沿Z轴方向0.1、0.15、0.2、0.25和0.3 m处的最大温升值。

表2和图5中,在沿管道中心同一位置处的最大温升值随功率增大呈线性增大,当热源功率达到400 W以上时,沿Z轴方向0.25 m处可以获得2 ℃以上的温升,可以用铂电阻式温度传感器进行准确测量,为井下电源的设计提供了依据。

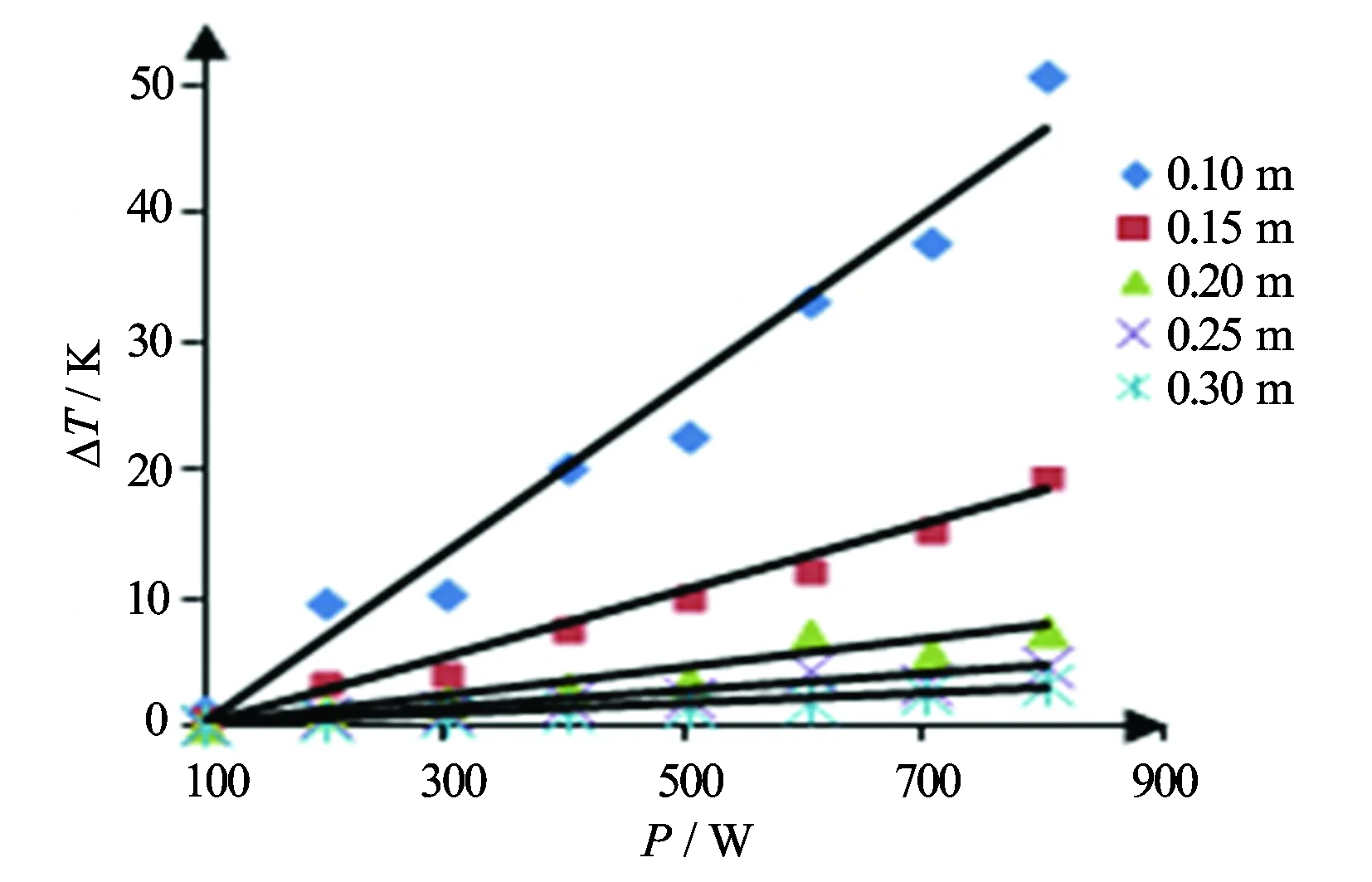
图5 不同流道位置处热源功率与最大温升的关系图

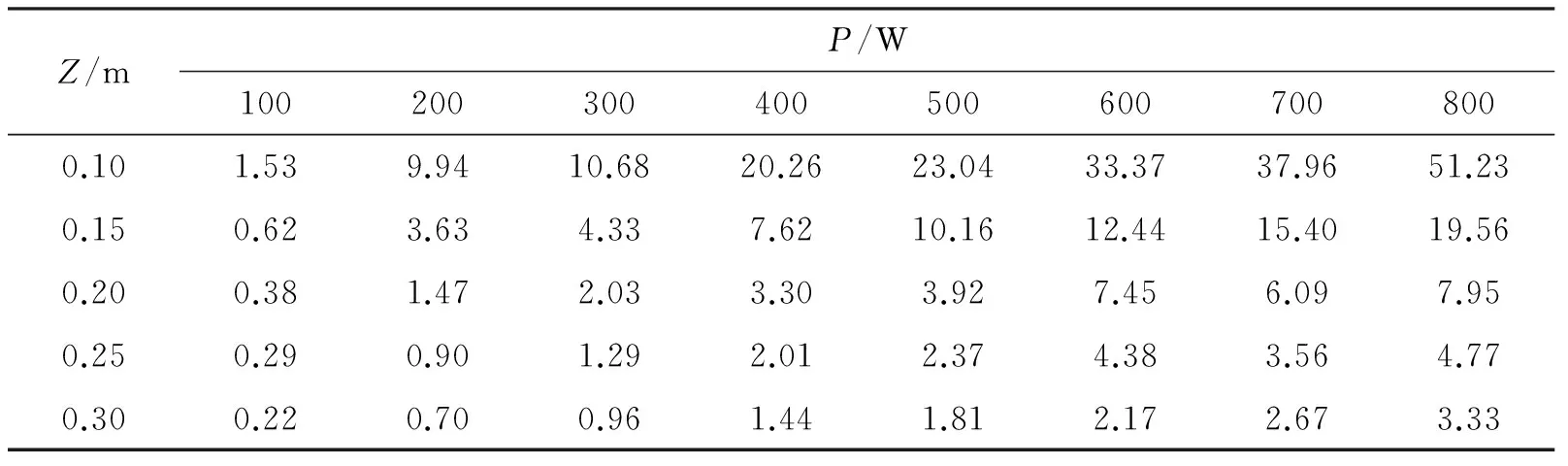
Z/mP/W1002003004005006007008000.101.539.9410.6820.2623.0433.3737.9651.230.150.623.634.337.6210.1612.4415.4019.560.200.381.472.033.303.927.456.097.950.250.290.901.292.012.374.383.564.770.300.220.700.961.441.812.172.673.33

3.4 热源在不同宽度加热脉冲作用下模拟结果分析

热示踪类测量仪器其热脉冲信号越窄测量的精度就会越高[11-12]。研究固定尺寸长方体型热源(长0.004 mm、宽0.002 mm、高0.005 mm)在同一加热功率(500 W)、同一流量(15 m3/d)下脉冲加热时间分别为0.5、1、1.5和2 s,流体初始温度300 K,得到流道内沿管道中心0.25 m处温升变化情况。

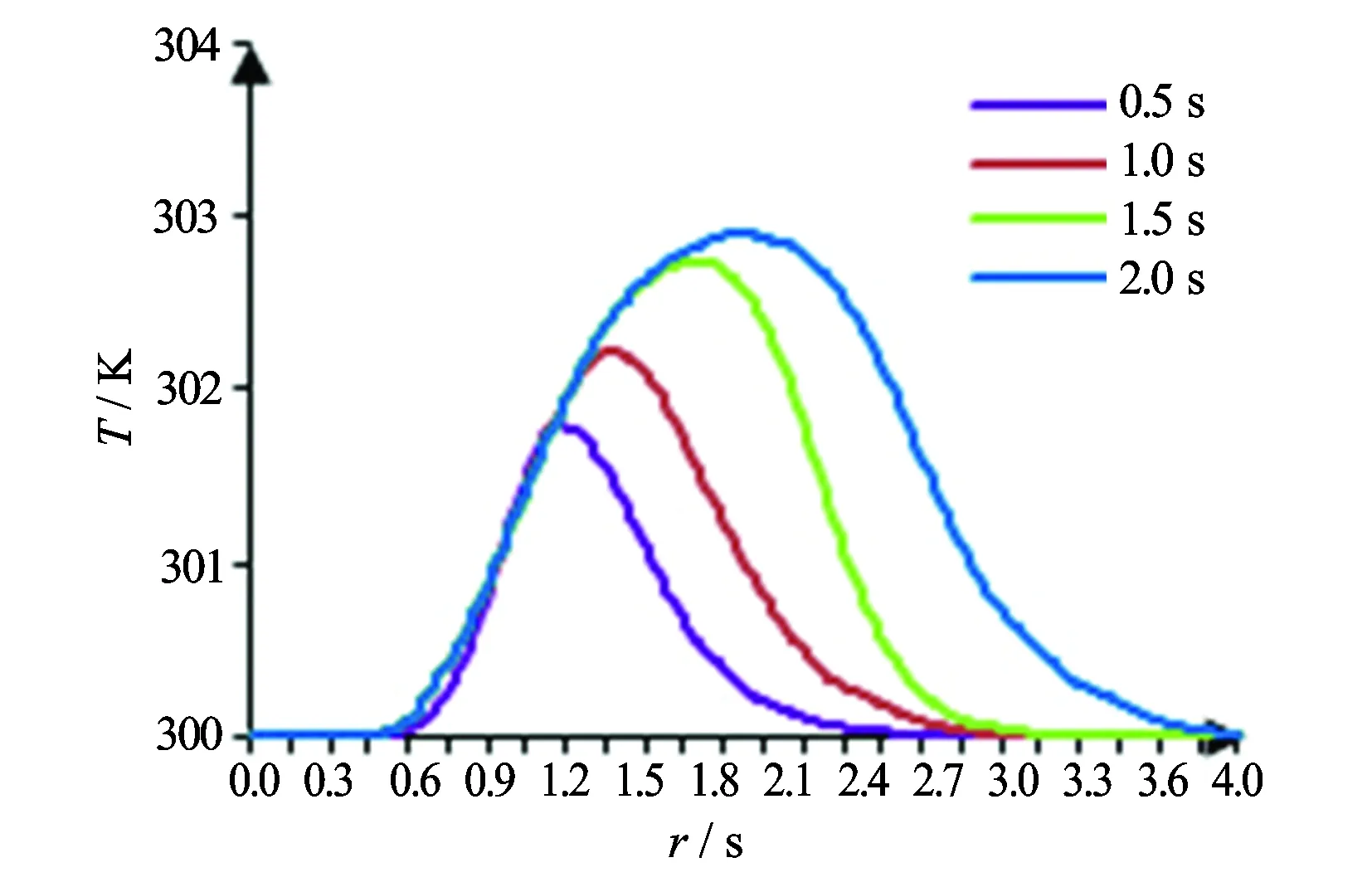
图6 不同宽度加热脉冲作用下Z=0.25 m处温度分布图

图6中,加热脉冲的时间越长在沿管道中心同一位置处的最大温升值越大;同时,脉冲的宽度也随之增加,在流量为15 m3/d时加热脉冲宽度为1 s时沿Z轴方向0.25 m处可以获得2 ℃以上的温升,可以用铂电阻式温度传感器进行准确测量,为井下电源的工作方式提供了依据。

4 总 结

(1) 在内径为37 mm的水平圆形管道内,放置不同形状、不同尺寸、不同加热功率、不同加热脉冲宽度的热源进行流固耦合的热传导数值模拟研究,得到流道内沿管道中心不同位置处的温升变化。

(2) 同一加热功率下采用长方体型热源可以获得更好的温升效果。

(3) 长方体型热源的宽和高不变的情况下改变长度,热源长度越大,获得的最大温升值越小;当流量达到15 m3/d时温升值不受长方体型热源长度的影响。

(4) 当热源功率达到400 W以上,加热脉冲宽度为1 s时可以在0～15 m3/d流量段内获得较好的温升效果,可以用铂电阻式温度传感器进行准确测量,为井下电源的设计和工作方式提供依据。

参考文献:

[1] 孟繁鑫, 张大林. 微小矩形通道内流动与换热特性 [J]. 南京航空航天, 2009, 41(3): 314-318.

[2] 高亚南, 张风琴, 郑枫, 等. 含有内热源的管道换热过程数值模拟与分析 [J]. 建筑热能通风空调, 2013(3): 81-83.

[3] 李兆敏, 张丁涌, 衣怀峰, 等. 多元热流体在井筒中的流动与传热规律 [J]. 中国石油大学学报: 自然科学版, 2012(6): 79-83.

[4] 夏国栋, 崔珍珍, 翟玉玲, 等. 长菱形微针肋热沉的流动与换热特性 [J]. 中国石油大学学报: 自然科学版, 2014, 38(2): 130-134.

[5] 朱曙光, 朱炳之, 刘心志. 热示踪法测量二次风风量实验研究 [J]. 江苏冶金, 2008, 36(2): 26-27.

[6] 陈繁, 王政. 热式质量流量计测量原理及选型 [J]. 现代冶金, 2013(1): 105-108.

[7] 邹德宁, 雷永平, 黄延禄, 等. 移动热源条件下熔池内流体流动和传热问题的数值研究 [J]. 金属学报, 2000, 36(4): 387-390.

[8] 孙翔, 刘传奇, 薛世峰. 有限元与离散元混合法在裂纹扩展中的应用 [J]. 中国石油大学学报: 自然科学版, 2013, 37(3): 126-130.

[9] Yanchang L, Dejun L, Ronghua X, et al. Research of Flow Measurement of Low-production Horizontal Well by Thermal Tracing and Development of Prototype [J]. International Journal of Digital Content Technology & Its Applications, 2012, 6(15).

[10] Lee T P, Chia Y, Chen J S, et al. Effects of Free Convection and Friction on Heat-pulse Flowmeter Measurement [J]. Journal of Hydrology, 2012, 428: 182-190.

[11] 赵娜, 王延军, 刘兴斌, 等. 水平井热示踪相关流量测量方法研究 [J]. 石油仪器, 2011, 25(2): 57-59.

[12] 冼海珍, 刘登瀛, 商福民, 等. 脉冲加热对振荡流热管传热性能的影响 [J]工程热物理学报, 2008, 29(8): 1363-1366.

[13] 樊冬艳, 姚军, 王子胜. 基于有限元的低渗透油藏水平井试井分析 [J]. 中国石油大学学报: 自然科学版, 2011, 35(2): 80-84.

[14] 曹宇光, 张卿, 张士华. 自升式平台齿轮齿条强度有限元分析 [J]. 中国石油大学学报: 自然科学版, 2010, 34(6): 120-124.

[15] 文闯, 曹学文, 吴梁红. 新型超声速旋流分离器设计及数值模拟 [J]. 中国石油大学学报: 自然科学版, 2010, 34(4): 119-126.