多极子阵列声波测井三维信息处理方法研究

李卫, 秦明景, 叶青, 陶果

(1.油气资源与探测国家重点实验室, 中国石油大学, 北京 102249; 2.北京市地球探测与信息技术重点实验室, 中国石油大学, 北京 102249)

0 引 言

地层速度信息在油气田勘探和开发阶段意义重大,可用于确定地层岩性、计算地层孔隙度、识别流体类型、计算岩石力学参数、评价井眼稳定性等。国内外对速度的轴向和周向信息研究较多,对速度的径向研究相对较少。地层速度的径向信息在评价井眼稳定性、监测泥浆滤液侵入情况、选择射孔位置和评价井壁应力集中等方面具有独特的优势。

利用偶极横波测井数据反演横波慢度径向剖面主要有2种方法:①Sinha等[1-3]提出将微扰法和BG理论相结合的方法得到地层横波慢度的径向变化,该方法得到的速度剖面为平均径向速度剖面;②Tang等[4-6]提出基于参数化的约束反演方法,该方法构建过渡带厚度和速度的目标函数,并对频散曲线高频段进行约束,降低反演结果非唯一性。以上2种方法都是利用参考模型和实际地层模型频散曲线之间的差异进行反演,因此,频散分析结果对反演结果的精度影响很大。

前人在反演偶极横波慢度的过程中,一般采用常规的频散分析方法,如加权频谱相干法、Matrix Pencil方法、Prony方法等,上述频散方法在分辨率、精度等方面存在不足。对频散分析方法进行研究发现,幅度和相位估计法(APES)是一种高性能的频散分析方法,该方法具有高信噪比和高分辨率的特征,是一种基于非参数估计的频散分析方法[7]。本文结合APES频散分析方法和高频约束反演法,通过提高频散分析结果的精度、降低偶极横波慢度径向剖面反演结果的非唯一性,提高反演结果精度。

1 幅度和相位估计法

假定任意多极子阵列声波测井数据频谱由各振型频谱和噪声频谱组合而成,并且各振型频谱由不衰减的复指数形式表示,则

n=1,2,…,N

(1)

式中,p为波形数据中存在的振型数;d为接收器间距;N为接收器个数;km为m阶模式波的波数(即km=ωsm,sm为m阶模式波的慢度);αm为m阶模式波幅度;vn为噪声信号频谱。

设计一个M抽头的滤波器,使某一波数为k的振型无损输出,同时压制其他振型和噪声信号,就可以转换为约束条件下的最优化问题

(2)

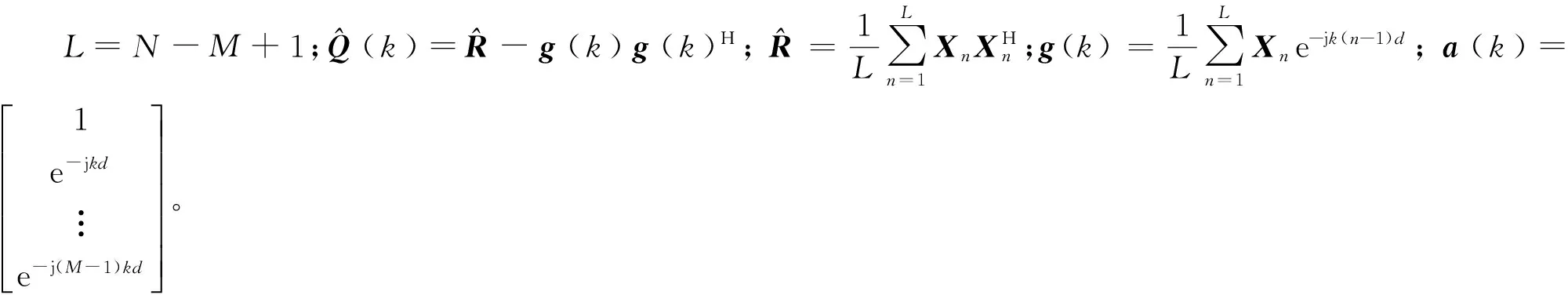
利用拉格朗日乘子法求解上面的条件极值问题,可得

(3)

根据滤波器权重和幅度谱之间的关系,可以得到幅度谱估计

(4)

2 约束反演法

研究表明,在低频段内当均匀模型的地层速度与变化地层近井眼地层速度基本一致时,均匀模型和变化地层模型的频散曲线很接近;相应地,在高频段内,当均匀模型的地层速度与变化地层原状地层速度基本一致时,均匀模型和变化地层模型的频散曲线基本匹配。当地层慢度径向存在变化时,偶极横波波形曲线以及频散曲线都会相应地发生变化。基于上述理论,可以建立目标函数

(5)

式中,vm为根据Δr和Δv建立地层模型后计算得到的频散曲线[即均匀(参考)模型频散曲线];vd为实际地层模型频散曲线;Ω为反演频率范围;vh为根据近井眼慢度建立的均匀模型,进行频散分析得到的结果;v1为近井眼慢度;Ω′为高频约束法选取的高频段,一般取8～10 kHz;λ为引入的系数,其大小与Ω和Ω′的比值大小有关,其主要目的是使式(5)右边的第1项和第2项在同一数量级上,保证高频段对目标函数的贡献。

根据目标函数二维图像,求取当目标函数取最小值时所对应的Δr、Δv,然后带入参数化的径向剖面表达式

(6)

式中,v0为原状地层横波速度;r0为井眼半径。

3 结果与分析

3.1 频散结果分析

加权频谱相干法是一种常用的常规频散分析方法,该方法是一种基于非参数估计的频散分析方法[8]。利用加权频谱相干法、幅度和相位估计法,分别对模拟数据和实际数据进行频散分析,两者的模拟数据频散结果见图1,实际数据频散结果见图2。

从图1和图2中可以看出,2种方法得到的频散分析结果具有很好的一致性,然而,图1(b)、图2(b)相对于图1(a)、图2(a)的结果,红色的峰脊更窄更尖,说明APES方法提取的慢度值更加准确,频散分析结果分辨率更高。

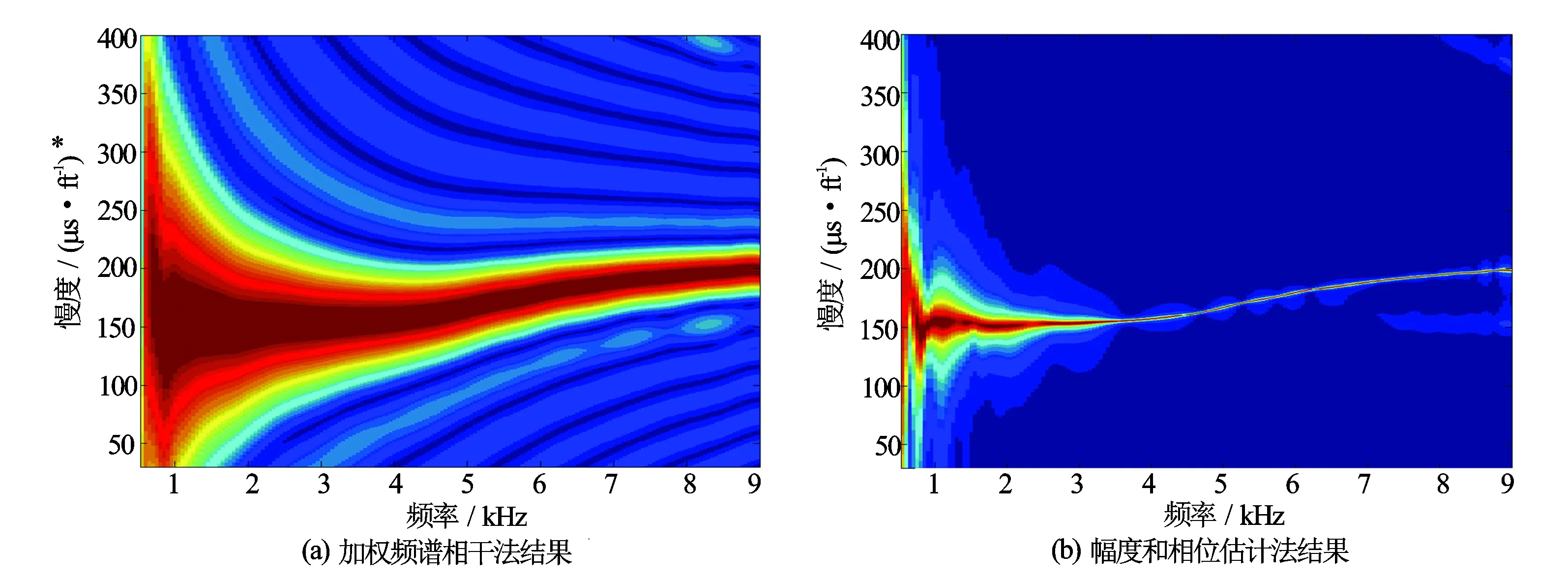
图1 模拟数据频散分析结果*非法定计量单位, 1 ft=12 in=0.304 8 m,下同

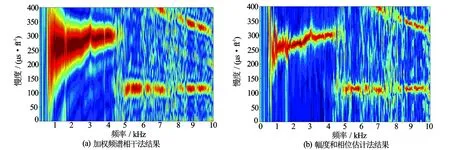
图2 实际数据频散分析结果

3.2 径向剖面反演结果分析

设定模型过渡带等效为多层介质模型,利用幅度和相位估计法对这2个模型正演得到的数据进行频散分析,得到频散曲线,将频散曲线带入目标函数,就可以得到目标函数二维谱。

图3 多层过渡带模型地层

该地层模型包括9个过渡带,各过渡带厚度和慢度都在变化,并且随着径向深度的变化,过渡带的速度呈递增趋势(见图3),多层过渡带模型地层参数见表1。图4至图7为多层过渡带高频不约束与约束情况下目标函数二维图像及其偶极横波慢度径向剖面反演结果。通过研究发现,频散曲线对纵波慢度不敏感,因此在该模型中设定纵横波速度比为1.8。多层过渡带模型进行高频约束反演计算目标函数时,约束系数λ=3。

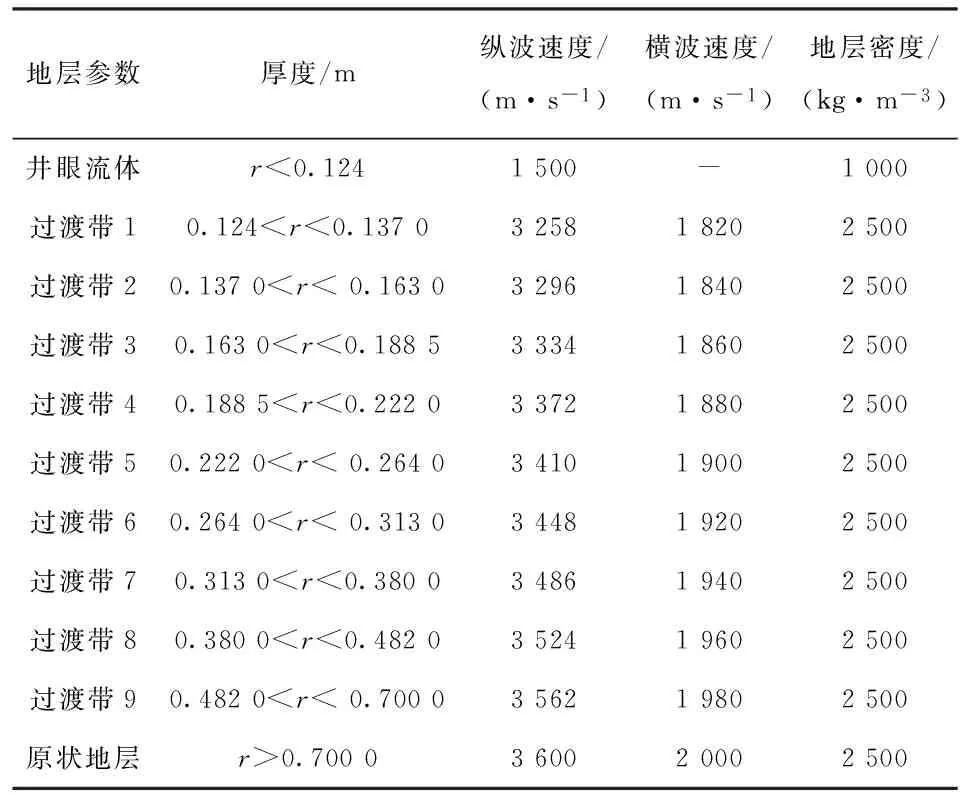
表1 多层过渡带模型地层参数

从单层过渡带模型和多层过渡带模型反演结果均可看出,高频约束反演法相对于高频不约束的情况,目标函数二维谱蓝色沟壑部分范围更小,反演得到的速度剖面更接近于实际地层模型,与实际地层模型慢度相对误差更小,说明高频约束会降低反演结果的非唯一性。图7中红色实线代表高频约束和不约束情况下相对误差的差值,可以看出随着距离井眼越近,二者的相对误差差值越大,说明在近井眼条件下高频约束相对不约束的情况优势更加明显。

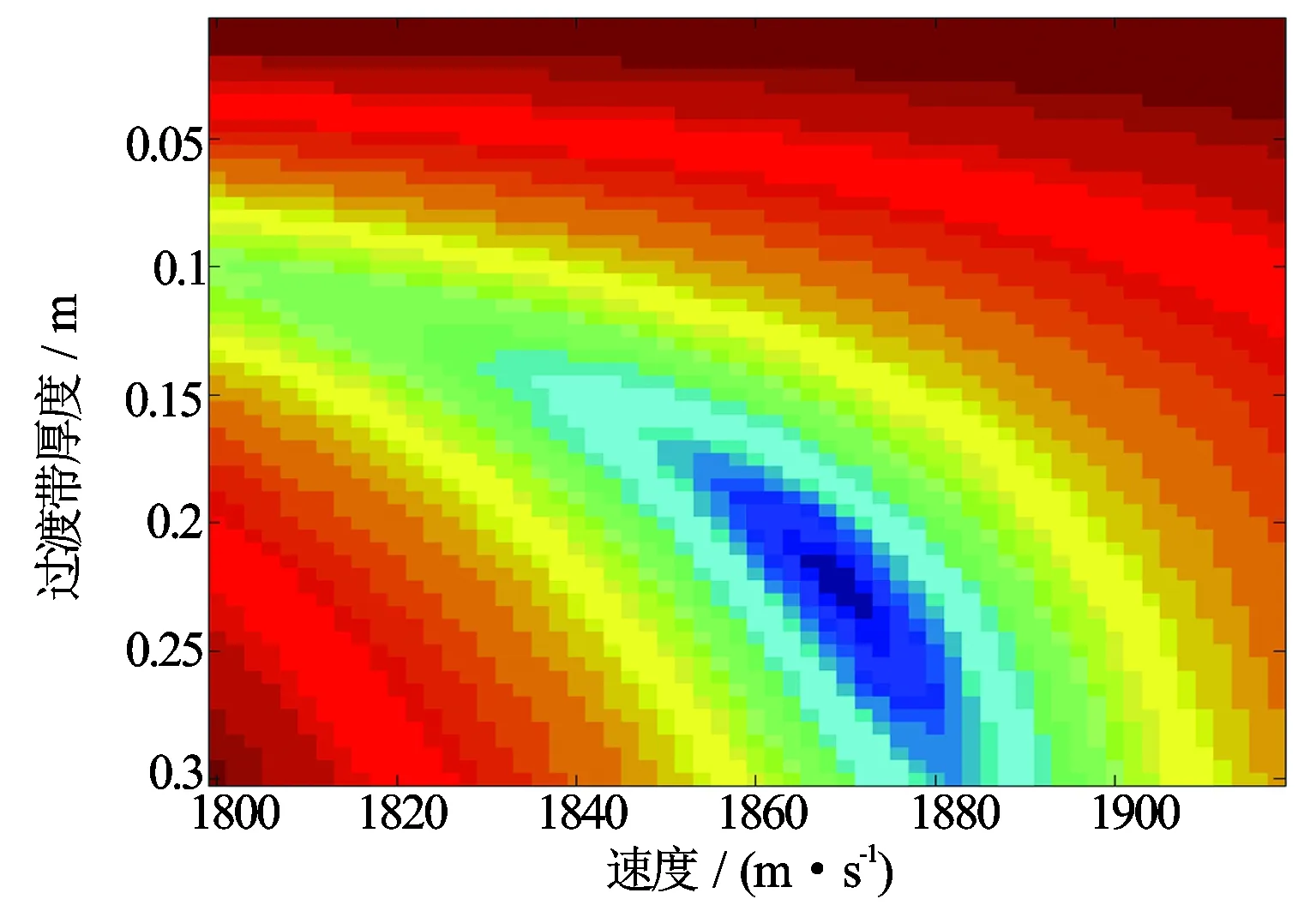
图4 多层过渡带高频不约束情况下目标函数二维图像

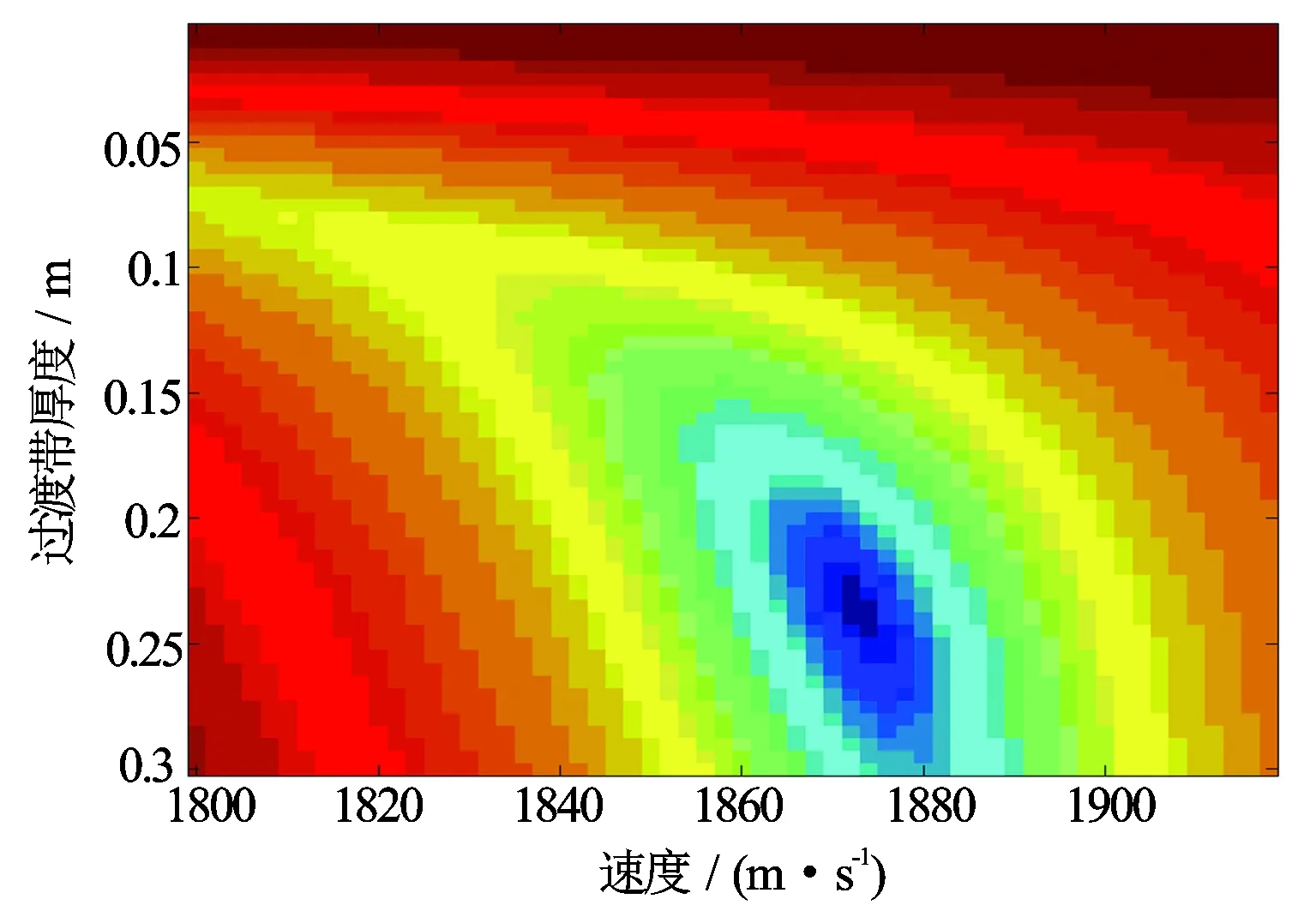
图5 多层过渡带高频约束情况下目标函数二维图像

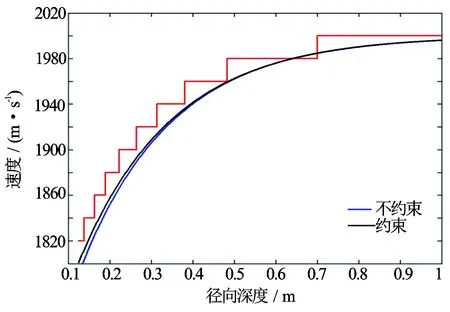
图6 多层过渡带高频不约束和约束情况下偶极横波慢度径向剖面反演结果(红色实线是图3所示地层模型的速度剖面)

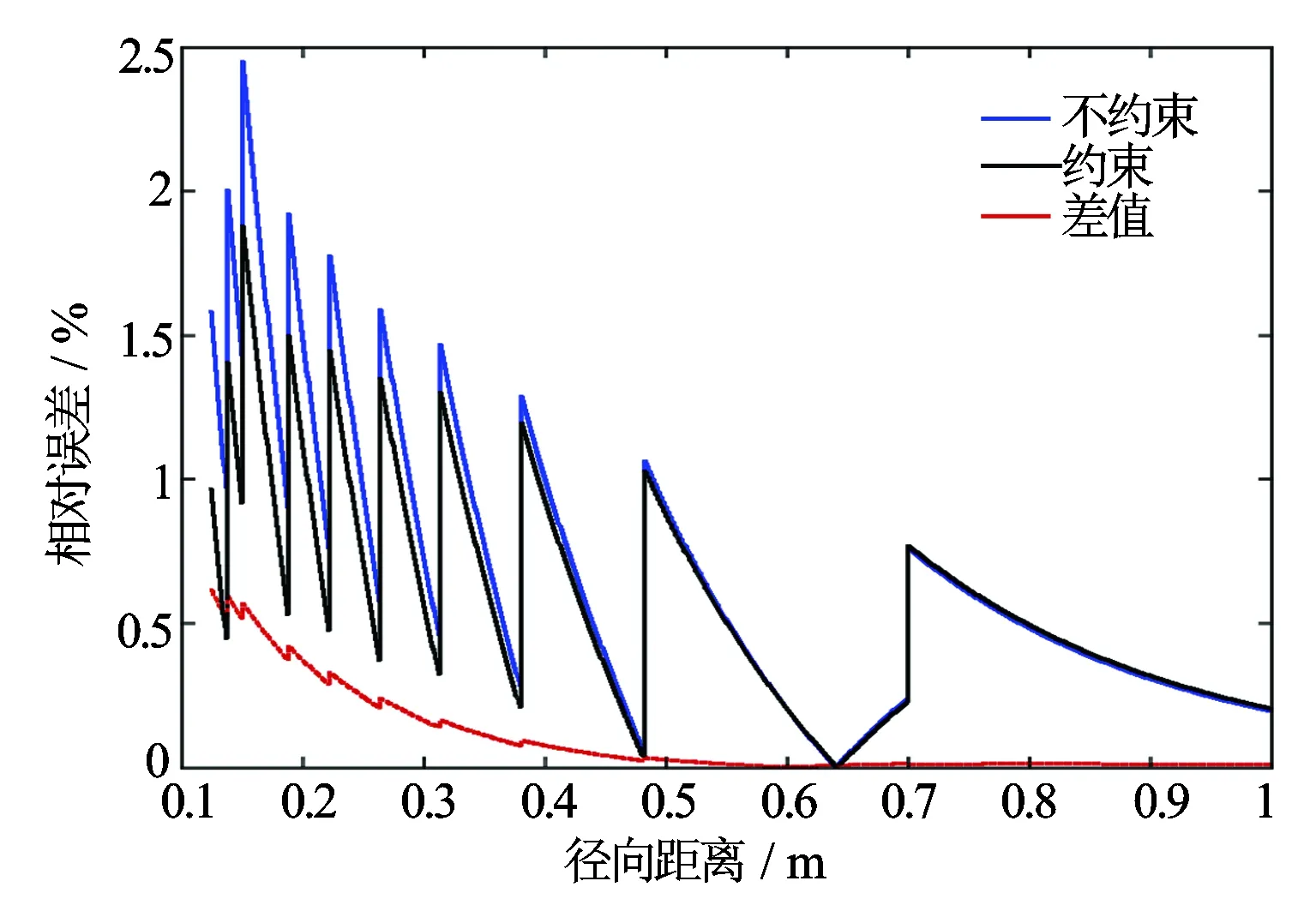
图7 高频不约束和约束情况下相对误差

这种精度的提高归功于对高频部分进行约束,高频部分约束可以加大高频部分在目标函数中的权重,高频部分更多反映的是近井眼地层的信息。

4 结 论

(1) 幅度和相位估计法相对于常规的频散分析方法具有更高的分辨率和精度。

(2) 利用幅度和相位估计法结合高频约束反演法能够得到比较准确的地层慢度径向剖面。

(3) 高频约束反演法得到的结果精度更高,尤其是对于近井眼地层而言。

参考文献:

[1] Backus G, Gilbert F. Uniqueness in the Inversion of Inaccurate Gross Earth Data [J]. Philosophical Transactions of the Royal Society of London, 1970, 266(1173): 123-192.

[2] Burridge R, Sinha B K. Inversion for Formation Shear Modulus and Radial Depth of Investigation Using Borehole Flexural Waves [C]∥SEG Expanded Abstracts, 1996: 158-161.

[3] Sinha B K, Vissapragada B, Renlie L, et al. Radial Profiling of the Three Formation Shear Moduli and Its Application to Well Completions [J]. Geophysics, 2006, 71(6): E65-E77.

[4] Tang X M, Patterson D. Mapping Formation Radial Shear-velocity Variation by a Constrained Inversion of Borehole Flexural-wave Dispersion Data [C]∥SEG Annual Meeting, Denver, 2010: 503-507.

[5] 赵龙, 唐晓明, 苏远大, 等. 横波速度径向层析成像方法及应用研究 [J]. 应用声学, 2014, 33(1): 9-15.

[6] Su Y D, Tang X M, Zhuang C X, et al. Mapping Formation Shear-velocity Variation by Inverting Logging-while-drilling Quadrupole-wave Dispersion Data [J]. Geophysics, 2013, 78(6): D491-D498.

[7] Li W, Guo R, Tao G, et al. Enhanced Dispersion Analysis of Borehole Array Sonic Measurements with Amplitude and Phase Estimation Method [C]∥SEG Annual Meeting, Las Vegas, 2012: 1-5.

[8] Nolte B, Rao VNR, Huang X. Dispersion Analysis of Split Flexural Waves [R]. Borehole Acoustics and Logging/Reservoir Delineation Consortia Annual Report, 1997.