基于储层分类的支持向量机渗透率预测

袁伟, 张占松, 张泽宇, 吕洪志, 李兴丽, 崔云江

(1.中海石油(中国)有限公司湛江分公司, 广东 湛江 524057; 2.长江大学油气资源与勘探技术教育部重点实验室, 湖北 荆州 434023; 3.中国地质大学, 湖北 武汉 430074; 4.中海石油(中国)有限公司天津分公司, 天津 300452)

0 引 言

通常,根据测井资料预测储层渗透率主要采用经验关系以及统计回归的方法[1],这种方法操作简单,但是计算精度却很难满足生产要求。自从神经网络被提出后,这一非线性非参数的回归方法被引入到油气储层参数评价中去,克服了常规统计回归方法的一些局限性,使得储层评价精度得到了进一步的提高[2-4]。但是,随着勘探开发的深入,测井所面临的地质环境和储层特征越来越复杂,尤其是在训练样本比较少时,神经网络预测储层参数的方法逐渐表现出自身的一些缺陷,比如训练中易出现局部极小、过学习、难以找到最优模型等问题[5]。另一方面,支持向量机这一专门针对小样本的机器学习方法逐渐发展起来,避开了传统的从归纳到演绎的过程,预测效率高,简化了通常的分类和回归等问题,在许多科学前沿领域取得了成功的应用[6-10]。

研究区属于三角洲前缘沉积,沉积微相主要有水下分流河道、远砂坝、支流间湾、河口坝。岩性主要为含岩屑长石石英砂岩,储层为高孔隙度高渗透性储层,孔隙度分布在26%～40%,渗透率分布在24～12 000 mD*非法定计量单位,1 mD=9.87×10-4 μm2,下同,分布范围广,层间渗透率突进系数Tk=4.5,层间渗透率级差Jk=250.9,层间非均质性强。同时,由于储层经过长期的注水开发,储层的物理性质和流体性质发生了很大的变化,加剧了储层的非均质程度。目前针对该区的渗透率预测方法主要是采用常规的回归统计模型,其根据孔隙度建立的渗透率预测模型预测精度较差,达不到生产实际的要求。本文尝试采用储层分类以及基于核学习理论的支持向量机方法,建立每类储层的渗透率预测模型,用渗透率相关属性变量预测各类储层的渗透率,以期获得优于常规预测方法的应用效果。

1 储层类型划分

1.1 储层类型划分方法

储层分类是储层精细评价的一种重要手段。研究区储层类型划分主要建立在储层孔隙结构相和成岩相分析的基础上,并借助综合化定量指标表征。采用孔隙度(φ)、渗透率(K)反映储层的物性特征;采用泥质含量(Vsh)反映储层的岩石相特征;采用IFZ、R35值反映储层的微观孔隙结构特征[11]。定义储层质量指标

(1)

标准化孔隙度指标

(2)

流动层带指标

(3)

由式(1)至式(3)可以得

lgIRQ=lgφZ+lgIFZ

(4)

式中,φ为地层孔隙度,小数;K为地层空气渗透率,mD;IRQ为储层质量指标,μm;φZ为标准化孔隙度,无量纲;IFZ为流动层带指标,μm。

一般认为,在IRQ与φZ的双对数坐标图上,具有相同IFZ值的样品点应该落在一条斜率为1的直线上,不同IFZ值的样品点应该落在与其平行的一条直线。同一直线上的样品点具有相似的孔喉结构,属于同一类储层,而不同类型的储层,其IFZ不同,因此可以根据计算的岩心IRQ、φZ值对储层进行分类。

1.2 取心段储层类型划分

根据IFZ的定义式可知,物性相差很大的储集层可能具有相同的IFZ值[12],这与同一类储层内物性基本一致的要求不符。为了尽可能地限制这一问题的出现,利用φ、K、R35对各类储层加以约束。R35值为压汞饱和度35%时的孔喉半径,在有岩心样品压汞分析的情况下,可以直接采用压汞曲线得到R35值。在没有压汞曲线的情况下,可采用Winland方程计算

lgR35=0.732+0.588 lgK-0.864 lgφ

(5)

根据密闭取心井×1井岩心分析数据,对岩心进行归位后,统计每一块岩心对应的φ、K、Vsh、R35、IFZ值,然后根据K均值聚类,把Ed油组划分为Ⅰ、Ⅱ、Ⅲ、Ⅳ共4类储层。图1为每类储层φZ与IRQ在双对数坐标轴下的关系图,每类储层的岩心基本分布在一条斜率为1的直线上,与上述理论分析一致。表1为Ed油组储层类型划分标准。

2 建立储层类型预测模型

2.1 支持向量机理论

支持向量机(SVM)[13]基本实现途径是采用结构风险最小化原理通过核函数将实际问题转换到高维特征空间,并在该高维空间中构造线性判别函数实现原空间中的非线性判别函数,寻找最优分类面(见图2),使其分类间隔最大。理论上,该算法能够得到全局最优解,避免了人工神经网络在实际应用中可能出现的局部极值问题。

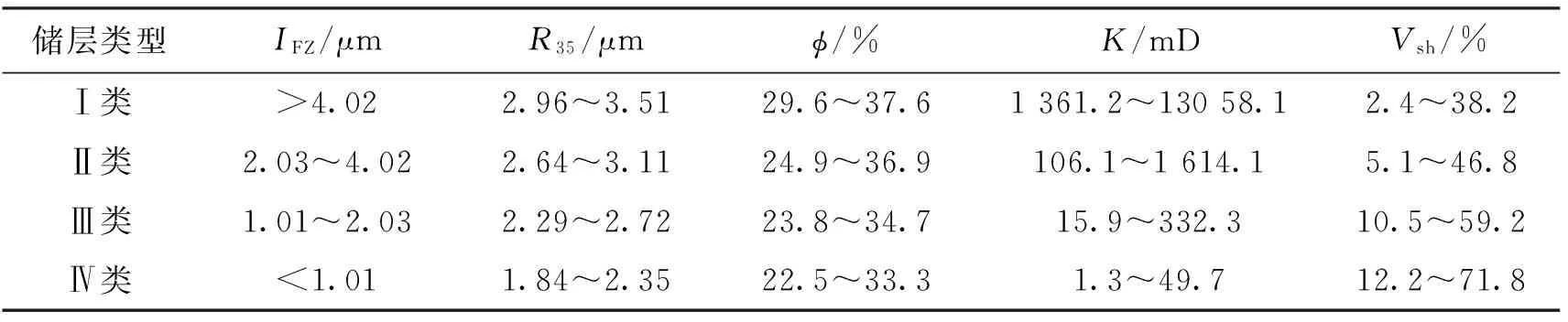
表1 Ed油组储层类型划分标准

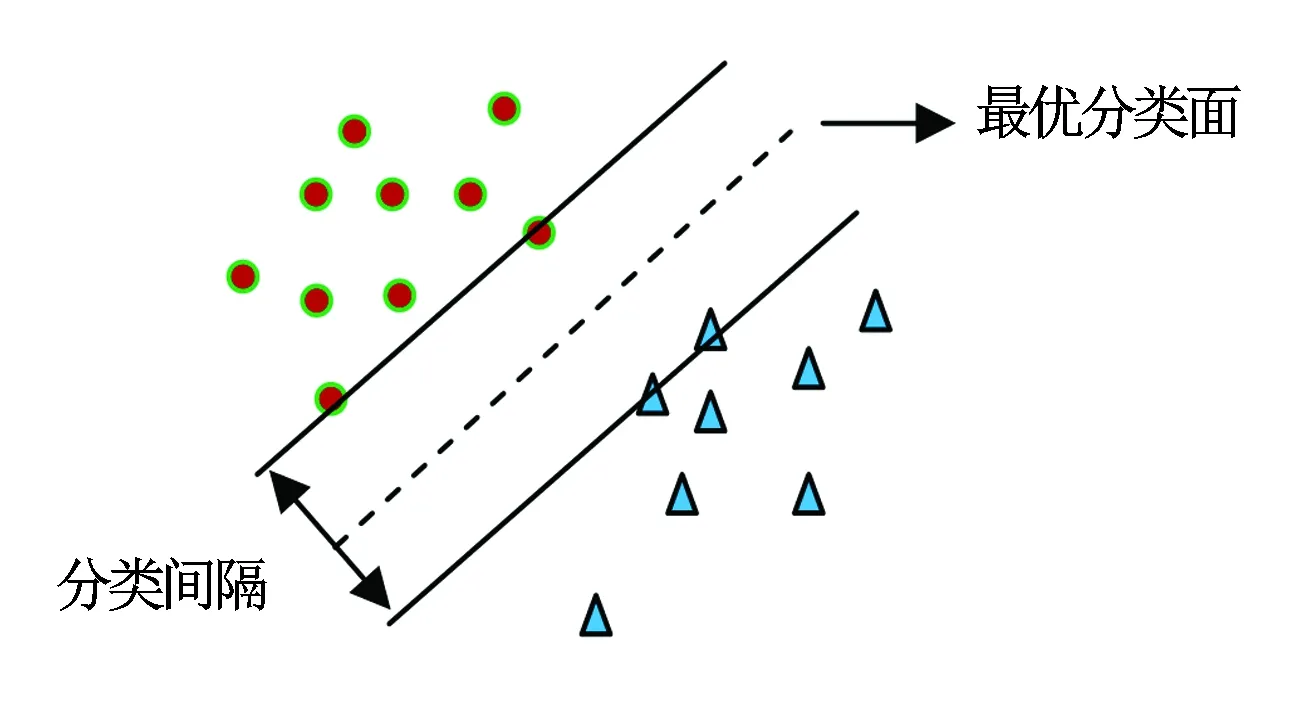
图2 最优分类面

2.2 储层类型划分

(1) 特征曲线的选取。选取具有代表性并能够反映储层孔隙结构的密度(DEN)、声波时差(AC)、补偿中子(CNL)、自然伽马(GR)作为支持向量机预测模型的输入训练变量,将储层类型作为输出。

(2) 数据的预处理。①学习样本的选取要尽量函盖4类储层类型,包含的范围要广;②选取作为输入训练样本的测井数据在数值上相差很大,处理时必然影响预测模型的精度,鉴于上述作为输入的测井数据均具有线性特征,所以处理时采用了线性归一化处理。

H*=(H-Hmin)/(Hmax-Hmin)

(6)

(3) 储层类型的预测。将归一化的数据作为输入样本输入模型进行训练,岩心样本共420个,选取300个作为训练样本,120个作为预测样本。在训练回归参数时,惩罚参数C、不敏感值X和核函数类型、核参数的选择等对训练的速度和函数估计器的推广性能都有较大影响,在此,支持向量机X的不敏感值取为0.01,核参数采用径向基RBF核K(x,xi)=exp(-‖x-xi‖2/2g2),最佳的优化参数根据网格法选取,即将C和g2分别取m个值和n个值,共有m×n个组合,对每个组合分别训练并估算其MSE误差,将这些组合中MSE推广误差最小的一个组合(C,g2)作为最优参数。这里选取m=n=12,C取值分别为|21、22、…、212|,g2取值分别为|2-6、2-5、…、25|,由此获得最优化参数C=4,e2=0.031,预测结果见表2,预测模型基本达到了正确划分储层类型的目的。

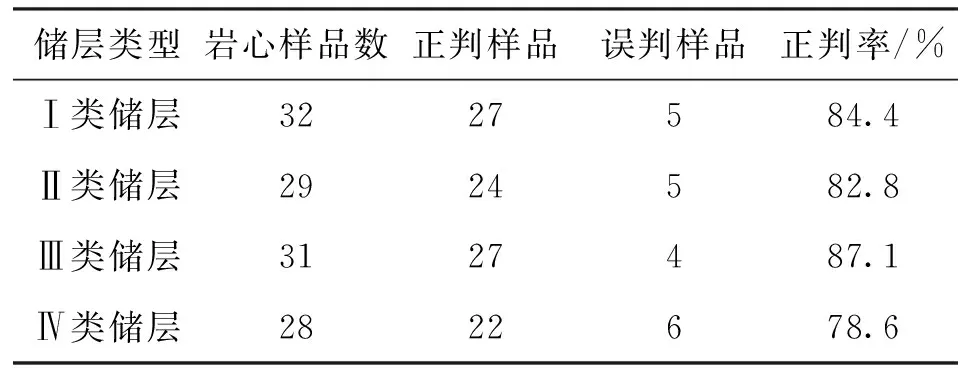
表2 储层预测模型预测结果

3 建立各类储层渗透率预测模型

(1) 对渗透率影响因素进行分析,提取可靠有代表性的测井值向量,最终确定以DEN、Vsh、φ作为输入训练参数。孔隙度φ、泥质含量采用式(7)至式(9)计算

(7)

(8)

(9)

式中,ρma为岩石骨架密度值,g/cm3;ρf为储层流体密度值,g/cm3;ρsh为泥岩密度值,g/cm3;GR为储层自然伽马测井值,API;GRmax为纯泥岩段自然伽马响应值,API;GRmin为纯砂岩自然伽马响应值,API;GCUR为地区经验系数,新地层取3.7,老地层取2。

(2) 根据储层类型预测模型对岩心数据进行分类,对每一类岩心渗透率有关的测井属性变量进行归一化处理。

(3) 将归一化的测井属性变量作为输入参数输入预测模型,通过学习训练建立每类储层的渗透率预测模型。在此,支持向量机X的不敏感值取为0.01,核参数采用径向基RBF核,使用网格法选择最佳的优化参数,Ⅰ类储层的优化参数C=64,g2=0.039;Ⅱ类储层的优化参数C=4,g2=0.027;Ⅲ类储层的优化参数C=32,g2=0.063;Ⅳ类储层的优化参数C=0.5,g2=0.030 5。

由图3、图4、图5可知,孔隙度回归渗透率模型计算的渗透率误差分布峰值为1.2,分类前的渗透率预测相对误差分布峰值为0.6,分类后的渗透率预测相对误差分布峰值为0.2,分类后的支持向量渗透率预测模型精度要比孔隙度回归模型以及分类前支持向量机预测模型精度有着明显的提高。

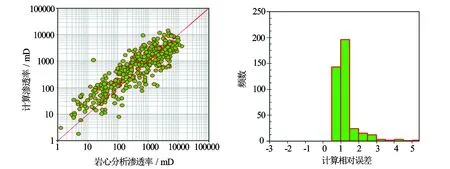
图3 孔隙度回归模型计算渗透率误差分析图

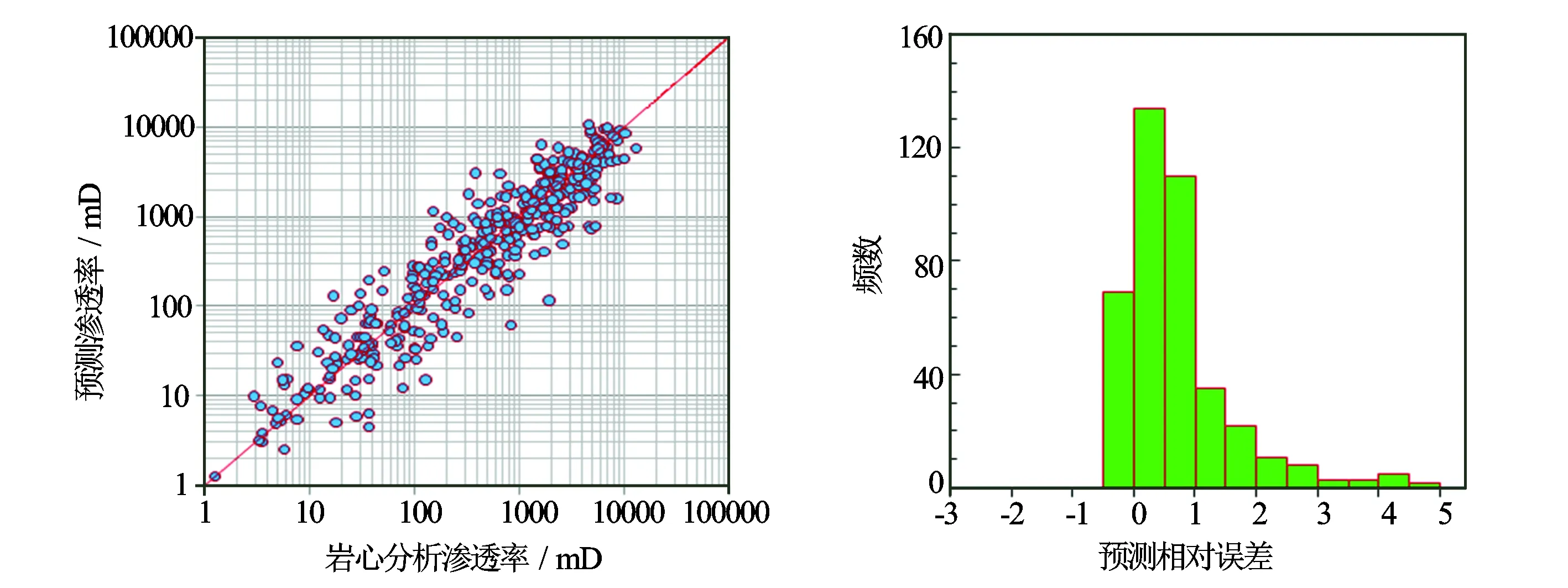
图4 分类前支持向量机渗透率预测渗透率误差分析图

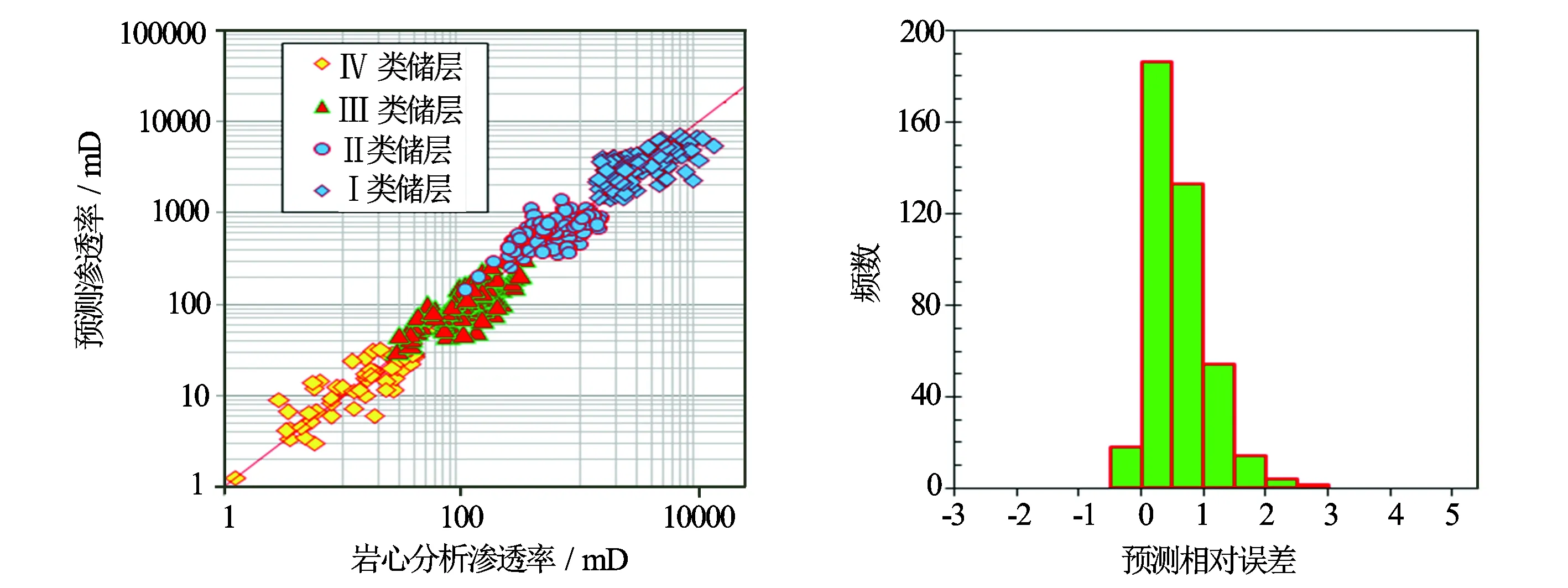
图5 分类后支持向量机渗透率预测渗透率误差分析图

4 模型应用效果

根据已建立的储层类型预测模型以及各类储层渗透率预测模型对取心井测试样本进行处理,并与岩心分析数据进行对比(见图6)。图6中第4道为计算的泥质含量Vsh,第5道为计算的孔隙度φ以及岩心分析孔隙度Core_φ,第6道分别为岩心分析渗透率Core_K、孔隙度统计回归预测渗透率φ_K、不分类支持向量机预测渗透率Predict_K以及基于储层分类的支持向量机预测渗透率CPredict_K。由图6可知,支持向量机预测的渗透率要比常规统计回归模型预测的渗透率精度要高,而基于储层分类的支持向量机预测方法预测效果最好,由此可见,文中提出的方法在研究区高孔隙度高渗透率储层的渗透率预测中具有一定的适用性,为该区的储层特征描述、油藏评价和开发提供了可靠的基础数据。

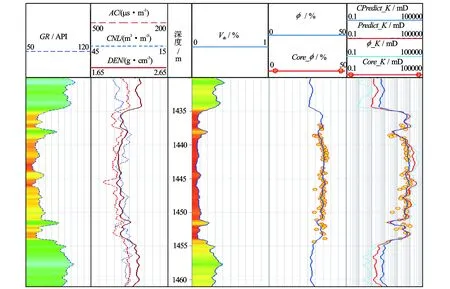
图6 渗透率预测模型效果对比图

5 结 论

(1) 根据流动带指标结合R35划分储层类型的方法,建立了研究区储层类型的的划分标准,所定标准具有一定的合理性。

(2) 采用基于结构风险最小化原理分别建立每类储层的渗透率预测模型,对研究区实际井资料进行处理,获得了满意的结果。该方法易于使用、稳定性强、预测准确性高、可信度强,对研究区储层评价以及注采开发方案的调整具有一定的指导意义。

(3) 该方法对其他储层参数如束缚水饱和度、残余油饱和度等的预测具有一定的借鉴和应用价值,为地质环境复杂、非均质性强的储层参数评价提供了新途径。

参考文献:

[1] 楚泽涵, 谢京. 用测井方法估算渗透率的评述 [J]. 石油勘探与开发, 1994, 21(1): 46-52.

[2] 陈蓉, 王峰. 基于MATLAB的BP神经网络在储层物性参数中的应用 [J]. 测井技术, 2009, 33(1): 75-78.

[3] 张丽华, 潘保芝, 庄华, 等. 低孔隙度低渗透率储层压裂后产能测井预测方法研究 [J]. 测井技术, 2012, 36(1): 101-105.

[4] 司马立强, 肖华, 袁龙, 等. 基于BP神经网络技术的储层流动单元研究 [J]. 测井技术, 2012, 36(4): 421-425.

[5] 余本国. BP神经网络局限性及其改进的研究 [J]. 山西农业大学学报: 自然科学版, 2009, 29(1): 89-93.

[6] 石广仁. 支持向量机在多地质因素分析中的应用 [J]. 石油学报, 2008, 29(2): 195-198.

[7] 石广仁. 支持向量机在裂缝预测及含油气评价应用中的优越性 [J]. 石油勘探与开发, 2008, 35(5): 588-594.

[8] Fatai Anifowose, AbdAzeem Ewenla, Safiriyu Eludiora. Prediction of Oil and Gas Reservoir Properties Using Support Vector Machines [C]∥International Petroleum Technology Conference, Bangkok, Thailand, 2012(7/8/9): 1-9.

[9] 陈华, 邓少贵, 范宜仁. 基于LS-SVM的测井物性参数的预测方法 [J]. 计算机工程与应用, 2007, 43(23): 208-210.

[10] Zhao Bo, Zhou Huawei, Li Xingong, et al. Water Saturation Estimation Using Support Vector Machine [C]∥SEG/New Orleans 2006 Annual Meeting: 1693-1695.

[11] 王月莲, 宋新民. 按流动单元建立测井储集层解释模型 [J]. 石油勘探与开发, 2002, 29(3): 53-55.

[12] 勒彦欣, 林承焰, 等. 关于用FZI划分流动单元的探讨 [J]. 石油勘探与开发, 2004, 31(5): 130-131.

[13] 祁亨年. 支持向量机及其应用研究综述 [J]. 计算机工程, 2004, 30(10): 6-9.