A note on ribbon elements of Hopf group-coalgebras

Zhao Xiaofan Wang Shuanhong

(Department of Mathematics, Southeast University, Nanjing 211189, China)



A note on ribbon elements of Hopf group-coalgebras

Zhao Xiaofan Wang Shuanhong

(Department of Mathematics, Southeast University, Nanjing 211189, China)

LetGbe a discrete group with a neutral element andHbe a quasitriangular HopfG-coalgebra over a fieldk. Then the relationship betweenG-grouplike elements and ribbon elements ofHis considered. First, a list of useful properties of a quasitriangular HopfG-coalgebra and its Drinfeld elements are proved. Secondly, motivated by the relationship between the grouplike and ribbon elements of a quasitriangular Hopf algebra, a special kind ofG-grouplike elements ofHis defined. Finally, using the Drinfeld elements, a one-to-one correspondence between the specialG-grouplike elements defined above and ribbon elements is obtained.

quasitriangular HopfG-coalgebra;G-grouplike element; ribbon element; Drinfeld element

In the theory of the classical Hopf algebras[1-2], one of the celebrated results is the theory of ribbon Hopf algebras, which plays an important role in constructing invariants of framed links embedded in 3-dimensional space[3]. One important aspect of ribbon Hopf algebras is the relationship between grouplike elements and ribbon elements[4].

As a generalization of ordinary Hopf algebras, Hopf group-coalgebras related to homotopy quantum field theories were introduced by Turaev in Ref.[5]. A purely algebraic study of Hopf group-coalgebras, such as the main properties of quasitriangular and ribbon Hopf group-coalgebras, can be found in Refs.[6-9].

In this paper, we consider the following question: for a groupG, how to use a special kind ofG-grouplike elements to describe the ribbon elements of a HopfG-coalgebra.

Throughout this paper, we letGbe a discrete group with a neutral element 1 andkbe a field. Assume thatHis a HopfG-coalgebra overk. Denote the set of allG-grouplike elements ofHbyG(H).

1 Preliminaries

Definition 1AHopfG-coalgebraH=({Hα},Δ,ε,S) is said to be crossed provided it is endowed with a familyφ={φβ:Hα→Hβαβ-1}α,β∈Gofk-linear maps (the crossing) such that for allα,β,γ∈G, 1)φβis an algebra isomorphism; 2) (φβ⊗φβ)Δα,γ=Δβαβ-1,βγβ-1φβ; 3)εφβ=ε; 4)φαβ=φαφβ.

Definition 2 A quasitriangular HopfG-coalgebra is a crossed HopfG-coalgebraH=({Hα},Δ,ε,S,φ) endowed with a familyR={Rα,β∈Hα⊗Hβ}α,β∈Gof invertible elements (theR-matrix) such that for allα,β,γ∈G, andx∈Hαβ,

Rα,βΔα,β(x)=σβ,α(φα-1⊗idHα)Δαβα-1,α(x)Rα,β
(idHα⊗Δβ,γ)(Rα,βγ)=(Rα,γ)1β3(Rα,β)12γ(Δα,β⊗idHγ)(Rαβ,γ)=[(idHα⊗φβ-1)(Rα,βγβ-1)]1β3(Rβ,γ)α23
(φβ⊗φβ)(Rα,γ)=Rβαβ-1,βγβ-1

Remark 1 LetH=({Hα,mα,1α},Δ,ε,S,φ,R) be a quasitriangular HopfG-coalgebra. The generalized Drinfeld elements ofHare defined byμα=mα(Sα-1φα⊗idHα)σα,α-1(Rα,α-1)∈Hα, for anyα∈G.

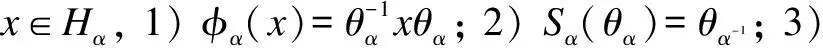
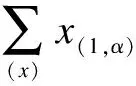
2 A New Description of Ribbon Hopf G-Coalgebras

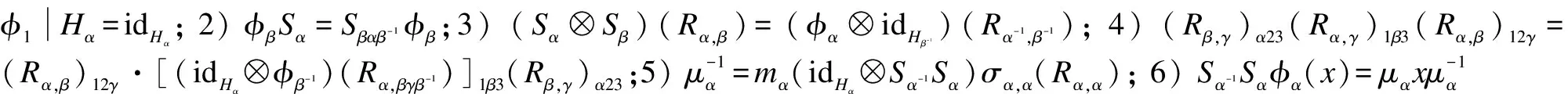
(2)

Proof We first check the identity (1). For anyα,β∈G

Next we show the proof of the identity (2). For anyα,β∈G, we have the following computations:

Lemma 3 LetH=({Hα},Δ,ε,S,φ,R) be a quasitriangular HopfG-coalgebra. Then for anyα,β∈G,

Proof Using Lemma 1 and Lemma 2, for anyα,β∈G, we compute

This completes the proof of the lemma.

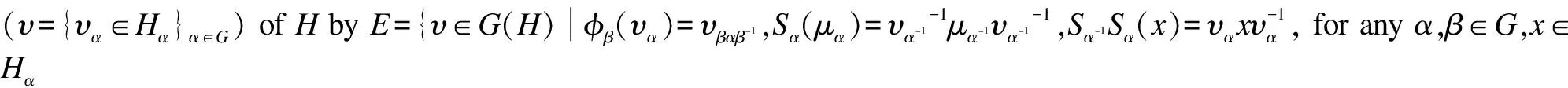
Theorem 1 Suppose thatH=({Hα},Δ,ε,S,φ,R) is a quasitriangular HopfG-coalgebra. Then there is a one-to-one correspondence betweenEandFdefined as above.

Let us prove the third condition. We compute

HencePis well defined. Secondly, we show thatPhas an inverse map. Define a mapQ:F→EbyQ(θ)=μθ={μαθα∈Hα}α∈G, for anyθ∈F. Clearly,PQ=idF,QP=idE. Following Ref.[6], we know thatQis well defined. This completes the proof of the theorem.

[1]Sweedler M.Hopfalgebras[M]. New York: Benjamin, 1969.

[2]Montgomery S.Hopfalgebrasandtheiractionsonrings[M]. Rhode Island: American Mathematical Society, 1993.

[3]Reshetikhin N Y, Turaev V G. Ribbon graphs and their invariants derived from quantum groups [J].CommMathPhys, 1990, 127(1): 1-26.

[4]Kauffman L H, Radford D E. A necessary and sufficient condition for a finite-dimensional Drinfel’d double to be a ribbon Hopf algebra [J].JAlgebra, 1993, 159(1): 98-114.

[5]Turaev V G. Homotopy field theory in dimension 3 and crossed group-categories[EB/OL]. (2000)[2013-07-01].http://arxiv.org/abs/math/0005291.

[6]Virelizier A. Hopf group-coalgebras [J].JPureApplAlgebra, 2002, 171(1): 75-122.

[7]Virelizier A. Graded quantum groups and quasitriangular Hopf group-coalgebras [J].CommAlgebra, 2004, 33(9): 3029-3050.

[8]Wang S H. Group entwining structures and group coalgebras Galois extensions [J].CommAlgebra, 2004, 32(9): 3417-3436.

[9]Wang S H. Group twisted smash products and Doi-Hopf modules for T-coalgebras [J].CommAlgebra, 2004, 32(9): 3437-3458.

关于Hopf群余代数ribbon元的注记

赵晓凡 王栓宏

(东南大学数学系, 南京 211189)

设G是一个带有单位元的离散群,H是域k上的拟三角HopfG-余代数. 考虑了H的G-群像元和ribbon元之间的关系. 首先证明了拟三角HopfG-余代数以及它的Drinfeld元的一些重要性质. 受到Hopf代数中群像元和ribbon元之间关系的启发, 定义了一类特殊的G-群像元. 最后利用Drinfeld元得到了所定义的特殊的G-群像元和ribbon元之间的一个一一对应关系.

拟三角HopfG-余代数;G-群像元; ribbon元; Drinfeld元

O153.3

Foundation items：The National Natural Science Foundation of China (No.11371088), the Natural Science Foundation of Jiangsu Province (No.BK2012736), the Fundamental Research Funds for the Central Universities (No.KYZZ0060).

：Zhao Xiaofan, Wang Shuanhong.A note on ribbon elements of Hopf group-coalgebras[J]．Journal of Southeast University (English Edition),2015,31(2):294-296．

10.3969/j.issn.1003-7985.2015.02.024

10.3969/j.issn.1003-7985.2015.02.024

Received 2013-10-27．

Biographies：Zhao Xiaofan (1986—), female, graduate; Wang shuanhong (corresponding author), male, doctor, professor, shuanhwang@seu.edu.cn．