Co-channel interference rejection for MIMO-OFDM systems

Pan Yunqiang Meng Xin Jiang Bin Gao Xiqi

(National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)



Co-channel interference rejection for MIMO-OFDM systems

Pan Yunqiang Meng Xin Jiang Bin Gao Xiqi

(National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)

A method based on the maximumaposterioriprobability (MAP) criterion is proposed to estimate the channel frequency response (CFR) matrix and interference-plus-noise spatial covariance matrix (SCM) for multiple input and multiple output orthogonal frequency division multiplexing (MIMO-OFDM) systems. An iterative solution is proposed to solve the MAP-based problem and an interference rejection combining (IRC) receiver is derived to suppress co-channel interference (CCI) based on the estimated CFR and SCM. Furthermore, considering the property of SCM, i.e., Hermitian and semi-definite, two schemes are proposed to improve the accuracy of SCM estimation. The first scheme is proposed to parameterize the SCM via a sum of a series of matrices in the time domain. The second scheme measures the SCM on each subcarrier as a low-rank model while the model order can be chosen through the penalized-likelihood approach. Simulation results are provided to demonstrate the effectiveness of the proposed method.

channel estimation; spatial covariance matrix (SCM) estimation; interference rejection; interference rejection combining (IRC) receiver

In order to satisfy the increasing demand for supporting more users with high data rates, modern cellular systems such as WiMax and LTE-advanced reuse the same frequency spectrum at each cell[1]. Such systems will encounter serious impairment due to co-channel interference (CCI) from neighboring cells. Hence, interference rejection is valuable and essential to interference-limited systems.

Some CCI suppression techniques, i.e., IRC[2]and fast-ML[3], model the CCI as a zero-mean, time uncorrelated and spatially colored stationary Gaussian random process, which needs to estimate the spatial covariance matrix (SCM) of interference-plus-noise and the channel frequency response (CFR) matrix of desired users. The conventional solution for the SCM estimation problem is the sample SCM estimate which is the maximum likelihood (ML) estimate in the case of Gaussian signals. However, in practical OFDM systems, the number of available residual samples is limited, thus only a rough estimation of SCM can be obtained and other measures should be taken into account to improve the accuracy of SCM estimation. Larsson[4]proposed a method by using a low-order time-domain model to improve the SCM estimation based on the fact that the SCM is the FFT of power spectrum of the interference-plus-noise. A structured model for SCM estimation was proposed in Ref.[5], which was obtained by eigenvalue decomposition (EVD) of the residual sample covariance matrix. Raghavendra et al.[6]proposed a method by parameterizing SCM on each subcarrier as a combination of several low-rank models, and each model has different probabilities. An improved SCM estimation exploiting the frequency correlation of the interferer channels was discussed in Ref.[7].

As mentioned above, the CFR matrix of desired users is also required for interference rejection. Conventional channel estimations in MIMO-OFDM systems have been investigated intensively[8]. However, in these studies only thermal noise was considered; i.e., the SCM was treated as an identity matrix, which clearly degraded the accuracy of the channel estimation when CCI was present. Also, on the other hand, channel estimation errors will result in error residual samples for SCM estimation. In this paper, a method based on the maximumaposterioriprobability (MAP) is proposed to effectively reduce the estimation errors of both CFR and SCM. Furthermore, we propose two schemes exploiting the number of interferers and the correlation between SCMs on different subcarriers. The first scheme transforms SCMs of all subcarriers back to the time domain via IFFT to obtain the correlation matrices followed by a temporal low-pass smoothing. Then, we represent each correlation matrix as a sum of a series of matrices described in Ref.[9] to maintain the semi-definite structure of SCM. The second scheme structures the SCM as a low-rank model with a few parameters through eigenvalue decomposition, and then smooths the low-rank matrix in the time domain. The low-rank model is somewhat similar to Ref.[5]. Ref.[5] assumed that the channels were frequency non-selective while there is no such assumption in this article. Both the two schemes not only keep the semi-definite of the obtained SCM, but also decrease the parameters to be estimated, which in turn improves the accuracy of SCM estimation. Finally, interference rejection combining (IRC) is employed on the receiver side for CCI suppression by using the estimated CFR and SCM.

1 System Model

Consider a MIMO-OFDM system equipped with transmit antennasNtand receiving antennasNr. Assume that there areNcsubcarriers for each OFDM symbol and the cyclic prefix is long enough to avoid inter-symbol interference (ISI). The channel is assumed to be a constant during one block of OFDM symbols, but changes independently from block to block. Here, one block of OFDM symbols consists of pilot symbolsNpfollowed by data symbolsNd. The received signal on pilot symbols is

yk,n=Hkxk,n+zk,n0≤k≤Nc-1, 0≤n≤Np-1

(1)

whereyk,n∈CNr×1andxk,n∈CNt×1denote the received signal and transmitted pilot symbol on thek-th subcarrier of then-th OFDM symbol in the frequency domain;Hk∈CNr×Ntis the MIMO channel matrix;zk,n～CN(0,Σk)∈CNr×1denotes the received interference-plus-noise, which is modeled as a colored Gaussian noise. The relationship between CFR and CIR is given by

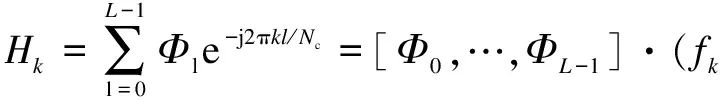
(2)

whereΦlis theNr×Nttime domain channel matrix;fk=[e0,e-j2πkl/Nc,…,e-j2πk(L-1)/Nc]T; andLis the number of channel taps for the desired user. Substituting Eq.(2) into Eq.(1), we can obtain

yk,n=Xk,nh+zk,n

(3)

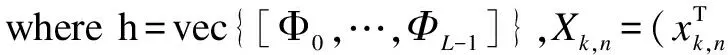
2 Estimation of CIR and SCM based on MAP Criterion

Collecting all theNcNpreceived pilots together, the least square (LS) estimation ofhis given as

(4)

(5)

(6)

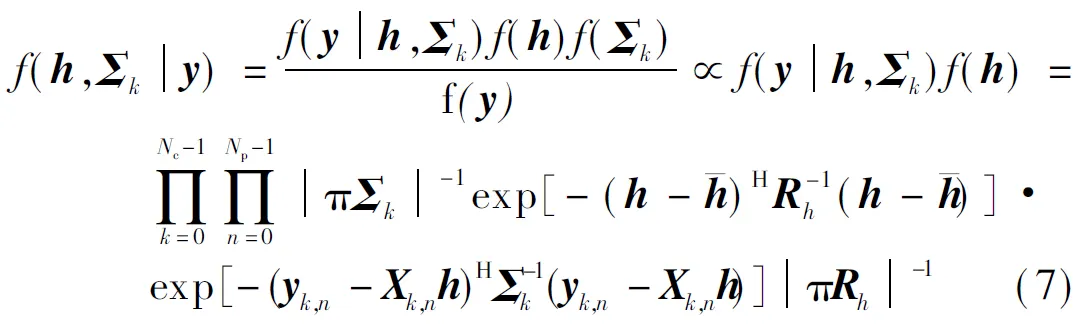
SinceΣkis positive semi-definite, the joint MAP estimation ofhandΣkcan be expressed as

(8)

In the next paragraph, we will propose two schemes to deal with the SCM, which not only move away the constraint in Eq.(8), but also decreases the number of estimated parameters ofΣk(k=0,1,…,Nc-1) to offer a better estimation performance. Then we design an iterative algorithm to solve Eq.(8).

2.1 Scheme 1

The received interference-plus-noise termzk(ignoring subscriptn) can be written as

(9)

wherevlis the time domain interference-plus-noise andLIis the maximum length of the interference channels. Hence, the SCM on thek-th subcarrier can be represented as

(10)

It is assumed that the transmitted time domain interference on different sampling times is uncorrelated and the received interference is the linear convolution of the transmitted interference and the CIR, soV(l,l′)=σ2INrifl≠l′, whereσ2is the noise variance. Thus, by replacingl-l′ withn, Eq.(10) can be simplified as

(11)

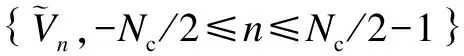
(12)

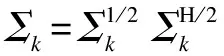
(13)

whereG=[G0,…,GLI-1],fLI,k=[1,e-j2πk1/Nc,…,e-j2πk(LI-1)/Nc]T. Finally, the SCM on the subcarrierkcan be expressed as

Σk=GQkGH

(14)

(15)

It is difficult to solvehandGat the same time. We take a more general method which solves one while treats the other as constant, and the iterative solution is considered. It is simple to find that, whenGis assumed to be fixed, and let the derivation of Eq.(15) with respect toh*to be zeros, the estimation of CIR is

(16)

In the same way, we can obtain the estimation of matrixG. If we estimateΣk(fork=0,1,…,Nc-1), the number of unknown parameters isNrNrNc. Now, we estimate matrixGinstead, and the number of unknown parameters is reduced toNrNrLI. In a real scenario,LI≪Nc, so the proposed method can improve the accuracy of the estimation effectively as it can significantly reduce the unknown parameters.

2.2 Scheme 2

Scheme 1 exploits the correlation of SCMs on different subcarriers to reduce the unknown parameters while the Scheme 2 in this subsection further exploits the number of interferers to improve the estimation accuracy. Assume that the interferer transmission is synchronized with that of the desired user; i.e., the cyclic prefix of the interference signal lines up with that of the desired signal. We assume that each interferer has only one antenna without loss of generality. Then, according to Eq.(1), the interference-plus-noise can be written as

(20)

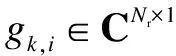
(21)

(22)

(23)

(24)

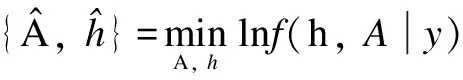
(25)

The same as in Scheme 1, taking the derivative with respect tohandA, we can obtain the estimation of CIR and matrixA, and thus SCM. In this proposed method, we only need to estimate matrixAwithNrd(2LI-1) unknown parameters instead of matricesΣk(fork=0,1,…,Nc-1) withNrNrNcunknown parameters. In most cases, Scheme 2 is more accurate compared to Scheme 1 since it estimates fewer unknown parameters and exploits more priori information such as the number of interferers.

We have assumed so far that the multi-tapLIof interference channels and the number of interferersdare known. In practice, they can be estimated by the MDL criterion[10-11].

3 Receiver with Co-Channel Interference

Interference rejection combining (IRC) is an efficient CCI suppression technique employed at the receiver side. It is based on the minimum mean square error (MMSE) criterion. Following Ref.[12], assuming that both the trueHand the trueΣare known, the IRC received data symbol is given as

(26)

4 Simulation Results

Simulations are presented in this section to describe the performance. We consider a block-fading MIMO-OFDM system withNc=64 subcarriers. The desired user goes through a channel with 8 taps in an exponential power delay profile (PDP). The interferers are equipped with one antenna. The signals are modulated to QPSK signal constellation. The channel coding is a convolutional code with a rate of 1/2.

We compare the FER performance under different scenarios and different estimation methods under the following conditions: 1) The ideal instantaneous SCM is known and the channel is estimated according to Eq.(16); 2) The ideal long-term SCM (defined asE{Σk}) for each subcarrierkis known and the channel is estimated according to Eq.(16); 3) The channel and instantaneous SCM are estimated by the algorithm discussed in Ref.[7]; 4) The channel and instantaneous SCM are estimated by the algorithm discussed in Ref.[4]; 5) The first scheme we proposed; 6) The second scheme we proposed.

In Fig.1, the mean square error (MSE) of the CFR is simulated under a different number of iterations. It is simple to conclude that the proposed algorithm has stable convergence after one iteration.

Fig.1 MSE of CFR under different number of iterations

Fig.2 compares the MSE of SCM under different schemes. The proposed schemes in this article show great performance and Scheme 2 outperforms Scheme 1. The MSE of SCM by using long-term SCM is the largest, for the long-term SCM is unable to characterize the instantaneous property of SCM in this case (INR=5dB).

Next, we derive the IRC receiver and compare the FER of the above six schemes. In Fig.3, the two proposed schemes providing 2 and 2.8 dB gain in SINR are compared to the method in Ref.[4] for the FER of 10-3,respectively, and there is less than a 0.5 dB gap between the second scheme we proposed and the method known as the ideal instantaneous SCM. The method in Ref.[7] with the worst-case performance for this method is invalid when the pilot symbol number is one. In Fig.4,the method in Ref.[7] performs better when using more pilots.

Fig.2 MSE of SCM vs. SINR (INR = 5 dB, Np=2, Nd=10, one interferer and Ll=2)

Fig.3 FER vs. SINR (INR = 10 dB, Np=1, Nd=5, one interferer and Ll=1)

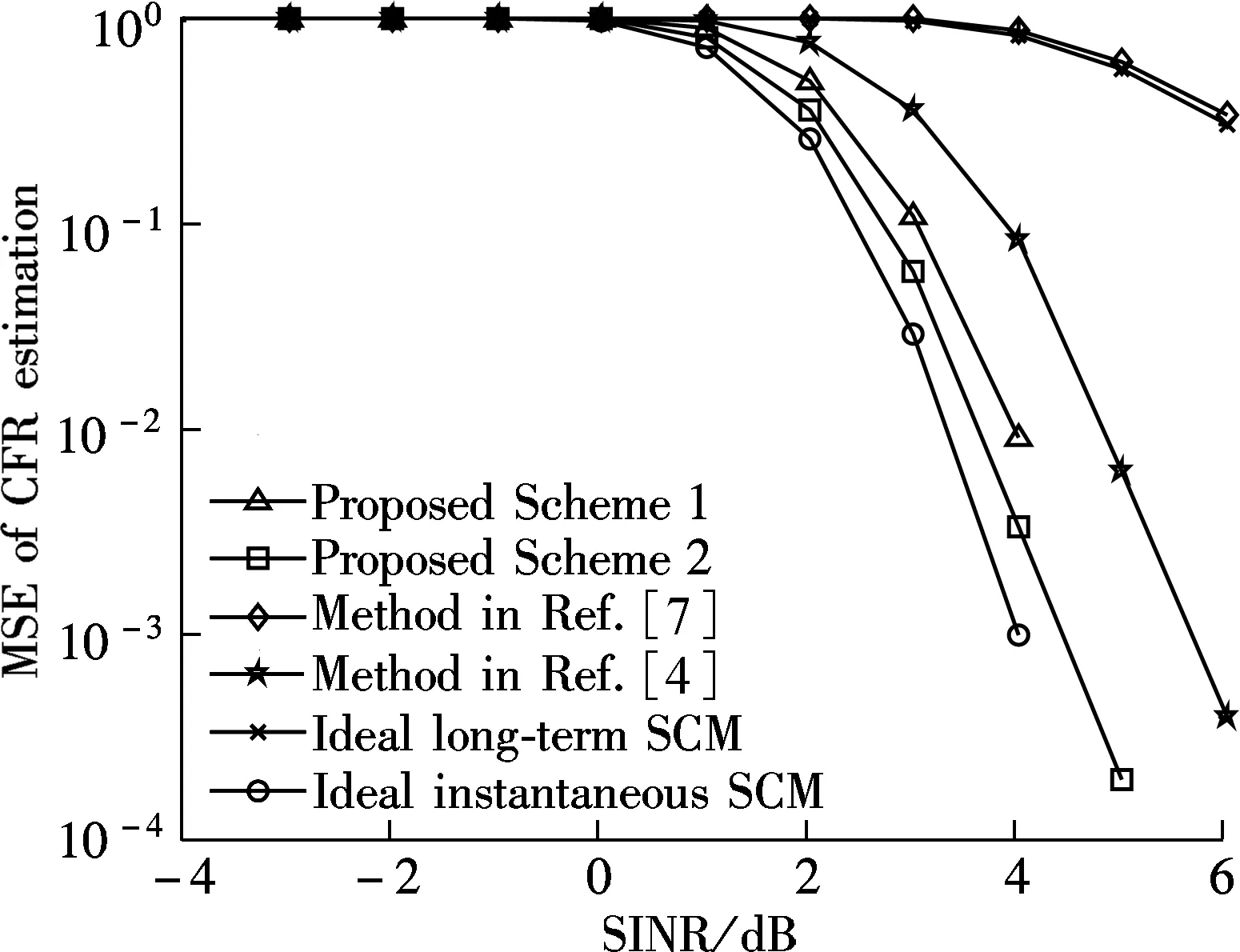
Fig.4 FER vs. SINR (INR = 5 dB, Np=2, Nd=10, one interferer and Ll=2)

5 Conclusion

In this paper, the method based on the MAP probability function is proposed for channel and SCM estimation of MIMO-OFDM systems. The SCM and CFR are estimated iteratively. Meanwhile, considering the structure of the SCM, two approaches adopting different matrix handling strategies can effectively reduce the estimation errors of both CFR and SCM. This paper adopts the IRC receiver based on the estimated CFR and SCM. Simulation results show that the proposed method can significantly improve the system performance.

[1]3rd Generation Partnership Project. TS 36.300: evolved universal terrestrial radio access (EUTRA) and evolved universal terrestrial radio access network (E-UTRAN); overall description; Stage2[EB/OL].(2009)[2015-02-01]. http://www.3gpp.org/dynareport/36300.htm.

[2]Lampinen M, Del C F, Kuosmanen T, et al. System-level modeling and evaluation of interference suppression receivers in LTE system[C]//ProceedingsoftheVehicularTechnologyConference(VTCSpring). Yokohama, Japan, 2012:6239964-1-6239964-5.

[3]Lomnitz Y, Andelman D. Efficient maximum likelihood detector for MIMO systems with small number of streams [J].ElectronicsLetters, 2007, 43(22): 1212-1214.

[4]Larsson E G. Semi-structured interference suppression for orthogonal frequency division multiplexing[C]//ProceedingsoftheIEEEInternationalSymposiumonSignalProcessingandInformationTechnology. Darmstadt, Germany, 2003:435-438.

[5]Ngren G, Ast L D, Ottersten B. Structured spatial interference rejection combining [C]//ProceedingsoftheEuropeanSignalProcessingConference. Tampere, Finland, 2000:435-438.

[6]Raghavendra M, Juntti M, Myllyla M. Co-channel interference mitigation for 3G LTE MIMO-OFDM systems[C]//ProceedingsofIEEEInternationalConferenceonCommunications. Dresden, Germany, 2009:1-5.

[7]Li Q, Zhu J, Guo X, et al. Asynchronous co-channel interference suppression in MIMO OFDM systems[C]//IEEEInternationalConferenceonICC. Glasgow, UK, 2007:5744-5750.

[8]Li Y. Simplified channel estimation for OFDM systems with multiple transmit antennas [J].IEEETransactionsonWirelessCommunications, 2002, 1(1): 67-75.

[9]Li L. A method to factorize the spectral density of multiple moving average processes [J].JSystemsSciMath, 1994, 7(1):69-76.

[10]Stoica P, Selen Y. Model-order selection: a review of information criterion rules [J].SignalProcessingMagazine, 2004, 21(4): 36-47.

[11]Rissanen J. Modeling by shortest data description [J].Automatica, 1978, 14(5): 465-471.

[12]Seethaler D, Matz G, Hlawatsch F. An efficient MMSE-based demodulator for MIMO bit-interleaved coded modulation[C]//ProceedingsoftheGlobalTelecommunicationsConference. Dallas, TX, USA, 2004:2455-2459.

MIMO-OFDM系统中同信道干扰抑制

潘云强 孟 鑫 江 彬 高西奇

(东南大学移动通信国家重点实验室,南京 210096)

针对MIMO-OFDM系统,提出了一种最大后验概率的信道矩阵和干扰协方差矩阵估计方法,并设计了迭代求解算法．利用所估计的信道矩阵和干扰协方差矩阵,采用IRC接收机完成同信道干扰的抑制．利用干扰协方差阵的共轭对称与半正定等特性,提出2种干扰协方差矩阵的处理方案以提高其估计精度．第1种方案将每个子载波上干扰协方差矩阵表征为一系列时域矩阵之和,第2种方案将每个子载波上的干扰协方差矩阵用低阶模型来建模,其中模型阶数通过最小描述长度算法估计．仿真结果表明了所提方案的有效性．

信道估计;干扰协方差估计;干扰抑制;IRC接收机

TN929.5

Foundation items：The National Natural Science Foundation of China (No.61320106003, 61222102), the National High Technology Research and Development Program of China (863 Program) (No.2012AA01A506).

：Pan Yunqiang, Meng Xin, Jiang Bin, et al. Co-channel interference rejection for MIMO-OFDM systems[J]．Journal of Southeast University (English Edition),2015,31(2):170-174．

10.3969/j.issn.1003-7985.2015.02.002

10.3969/j.issn.1003-7985.2015.02.002

Received 2014-09-04.

Biographies：Pan Yunqiang(1989—),male,graduate; Gao Xiqi(corresponding author), male, doctor, professor, xqgao@seu.edu.cn.