波动光学条纹公式及其条纹级次的讨论
2015-05-08王小平许佳捷
王小平,江 键,许佳捷
(第二军医大学 基础部数理教研室,上海 200433)
波动光学条纹公式及其条纹级次的讨论
王小平,江 键,许佳捷
(第二军医大学 基础部数理教研室,上海 200433)
文中就如何正确书写波动光学的条纹公式进行了讨论。从光的干涉和衍射条纹与光程差之间的关系出发,分析了杨氏双缝、薄膜干涉和单缝衍射相关公式中正、负符号的问题,条纹级次的取值范围及其对应的物理意义,并介绍了求解光栅衍射条纹数目的一般方法。
干涉;衍射;条纹公式;条纹级数
波的干涉、衍射是指由波的叠加而引起波的强度重新分布的现象。对光波而言,这种叠加区域表现为具有某种规律分布的明暗相间的条纹。而条纹的形状、位置、分布、移动以及数目等,则是光波干涉和衍射中讨论的主要问题。条纹在屏上的位置可用离开屏中心(主光轴与屏的交点)的坐标x或与主光轴的夹角φ来表示。一般情况下,干涉条纹的分布具有一定的对称性,明纹之间、暗纹之间,以及明纹和暗纹之间都存在一定的函数关系,因此,常用一组整数k来对条纹进行编号,由此可方便、简捷地描述条纹的空间位置、分布和移动等,这组整数被称为条纹级数(order number)或条纹级次[1]。
当赋予了条纹级次的物理含义后,k取值时就不能只满足光程差的关系式,还应考虑k的取值涉及了明、暗条纹公式的关联等。因此,何种情况下k的取值不能为零?什么情况下条纹公式中不出现“±”符号?k的最大值及其数目是多少?对这些问题的讨论,将有助于对光程差、相位差以及条纹空间分布等概念的理解和掌握。
1 杨氏双缝干涉条纹级数的取值
现将国内影响力较大的一些教材[1-4]中,有关杨氏双缝干涉条纹公式部分摘录如下[3]:按干涉条件,若相位差Δφ=±2kπ(k=0,1,2,3,…),即
δ=±kλ(k=0,1,2,3,…)
(1)
则相遇点P处是亮纹(各明纹中心最亮的点),相应明条纹的坐标
(2)
式中:k=0,相应于在O点处的中央明条纹;k=1,k=2,…,相应的明条纹,分别称为第一级明纹,第二级明纹,……
如果P处是暗的,按干涉条件则有
(3)
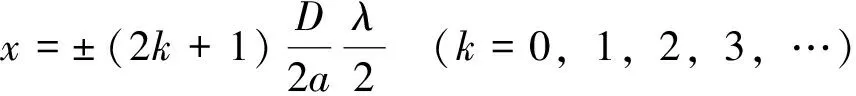
(4)
式(3)和式(4)中等号右端的“±”号表示明、暗条纹在中央明条纹(k=0)两侧对称分布。由于相邻级次明条纹(或暗条纹)相应的光程差相差一个波长,条纹的级次越高,其相应的光程差越大,级次高的条纹离开中央明纹距离越远。
我们注意到上述教材给出的光程差或条纹公式中k的取值均有0项,对式(2)而言物理意义明确,然而对式(4)而言则出现了“0级暗纹”,而在屏中央同一处不可能同时出现干涉相长、相消的情况,因此,屏中央不可能同时出现0级明纹和0级暗纹。
为避免“0级暗纹”的出现以及k从1开始取值又会漏掉紧挨中央明纹两侧的暗纹,式(3)和式(4)可修正为以下形式:
(5)
或
(6)
值得注意的是,“±”号放入暗纹公式中与放在k的取值前,结果是不一样的:
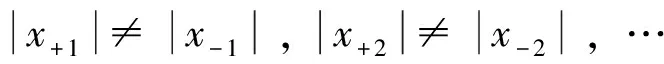
2 薄膜干涉中条纹级数的取值
如前所述,条纹公式的正、负号表示同一级条纹在零级明纹两侧对称分布,即相干光束抵达一处条纹的光程差始终大于零,而另一对称处的光程差等值且始终小于零。因此,若叠加区域的光程差只存在始终大于零(或小于零)的情况,则条纹公式中将不出现“±”符号。薄膜干涉讨论的是薄膜上、下表面分别反射的两束反射光(或两束透射光)产生的干涉,无论是等倾干涉还是等厚干涉,两束反射光(或两束透射光)的光程差只可能大于或等于零,因而在薄膜干涉公式中,无论是明纹还是暗纹,均不出现“±”号。
在薄膜干涉中,空气劈尖(等厚)干涉的明纹条件为:
(7)
式中:k不取0,是因为构成劈尖的两块玻璃片相接触处(棱边)e=0。由于“半波损失”的存在(式中的λ/2),即光程差不等于0而等于λ/2,为暗纹条件,故明纹的条纹级次k值须从1开始。
但是,劈尖及其上方和下方折射率满足一定条件时,条纹级次k值也可从0开始。设劈尖的折射率为n2,其上方和下方的折射率分别为n1和n3,若n1
当平行单色光垂直照射到牛顿环装置上的平凸透镜后,经过空气层上下表面反射后的两束光存在光程差,它们在平凸透镜的凸面相遇后将发生干涉,形成以平面玻璃板接触点为中心的一系列明暗相间的同心圆环。在接触点处,d=0,但由于存在相位突变,有一个附加光程差λ/2,所以在反射光看到的牛顿环中心是暗斑,此时与空气劈尖棱边的情况相同。
3 单缝衍射条纹中k的取值
单缝衍射条纹的明、暗公式分三种情况
1)暗条纹中心
Δ=asinφ=±kλ(k=1,2,3,…)
(8)
2)明条纹中心
(9)
3)中央明纹中心
φ=0
(10)
上述明、暗条纹公式中,k取值均不包含0。对暗纹而言,若k=0,则φ=0,衍射角为0的方向对应于光屏中心,而此处为中央明纹。故暗条纹级次的取值为k=1,2,3,…,它对称分布在中央明纹的两侧。由式(9)可以看出,若k=0,则Δ=asinφ=±λ/2,其物理含义是单缝波阵面在±φ方向所有子波到达光屏的最大光程差为λ/2,正好为一个“半波带”,为亮纹,但由于衍射条纹处在中央明纹区内,并不是明纹中心。因此,单缝衍射的中央明纹是单独讨论的,即φ=0方向上为中央明纹中心。
4 光栅衍射明纹(谱线)的级次
光栅衍射图样是由来自每一个单缝上若干子波以及来自各单缝对应的子波彼此相干叠加而形成,光栅衍射光强分布曲线的包迹(即曲线轮廓)与单缝衍射曲线强度曲线轮廓一样,因此,它是单缝衍射和多缝干涉的总效果。
当一束单色光照射在光栅上时,各狭缝的光线因衍射而向各方向传播,经透镜会聚相互产生干涉,并在透镜的焦平面上形成一系列明暗条纹。如图1所示。
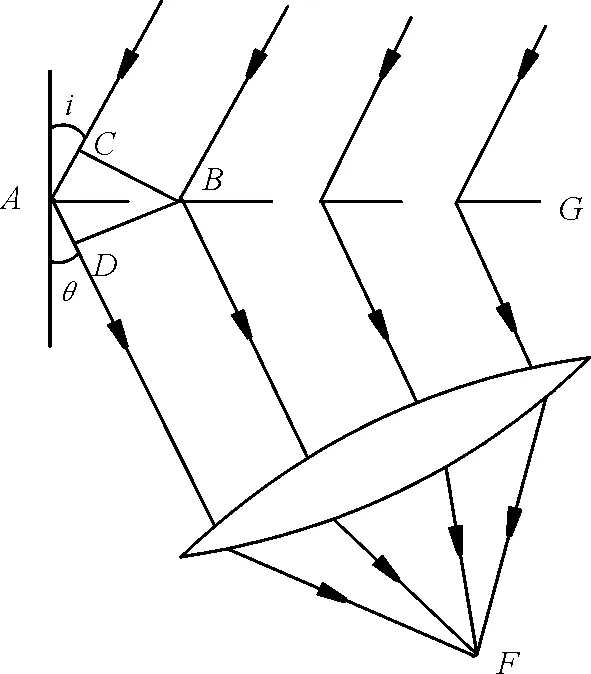
图1 光栅衍射图
有一束单色平行光与光栅的法线成i角,入射到光栅上产生衍射;出射光夹角为θ。从B点引两条垂线到入射光C和出射光D。如果在F处产生了一个明条纹,其光程差CA+AD必等于波长λ的整数倍,即d(sinθ± sini)=±kλ,式中θ、i均取正值,入射光线与衍射光线处在光栅法线同侧取“+”,在异侧取“-”;若平行光垂直入射,i=0,光栅方程变为dsinθ=±kλ,式中k(=0,1,2,3,…)为衍射眀纹(光谱)的级次。
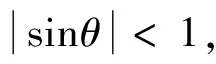
若平行光以与光栅的法线成i角入射到光栅时,光栅方程变为d(sinθ± sini)=±kλ,此时垂直于光栅方向上的两侧条纹不再对称,令sinθ=1,kml=d(1+sini)/λ,kmr=d(1-sini)/λ,显然,其中kml比垂直入射时的km值大,而kmr比km值小。因而,在其他条件不变的情况下,倾斜入射时可以观察到较高级次的条纹。
5 结束语
对于杨氏双缝实验,明条纹公式中的条纹级次k可取零,且只取正整数;薄膜干涉条纹公式中不出现“±”号,劈尖干涉中明条纹级次k是否取零取决于劈尖折射率与上、下方折射率的关系,当三方折射率不满足n1
[1]David Halliday,Robert Resnick,Jearl Walker.Fundamentals of Physics[M].8th Ed.New York:Wiley,2008:1189-1190.
[2]福里斯,季莫列娃.普通物理学(第三卷,第一分册)[M].2版.吉林大学物理系普通物理教研室,程路,译.北京:人民教育出版社,1963:32-33.
[3]程守洙,江之永.普通物理学(第三册)[M].4版.北京:高等教育出版社,1982:8-9.
[4]母国光,战元令.光学[M].北京:人民教育出版社,1979:205-206.
Discussion on Fringe Formula and Fringe Order in Interference and Diffraction
WANG Xiaoping, JIANG Jian, XU Jiajie
(Department of Mathematics and Physics, The Second Military University, Shanghai 200433, China)
Based on the physical meaning of fringe formula in interference and diffraction, this paper analyses the symbol problems of formula on Young’s double slit and thin film interference and single slit diffraction as well as discuses the values range of order number, and introduces a general method for solving the grating diffraction fringe number.
interference; diffraction; fringe formula; order number
2014-02-18;修改日期: 2014-03-29
军队院校物理教育教学研究基金资助课题(JWJ2012013)。
王小平(1960-),男,学士,副教授,主要从事医用物理学教学及科研工作。
O436.1
A
10.3969/j.issn.1672-4550.2015.01.002
