弹性混凝土与钢组合梁的疲劳性能分析及寿命预测

李自林 邢 颖 韩庆华,3 郭 琪

(1天津大学建筑工程学院,天津300072)(2天津城建大学天津市软土特性与工程环境重点实验室,天津300384)(3天津大学滨海土木工程结构与安全教育部重点实验室,天津300072)

弹性混凝土与钢组合梁的疲劳性能分析及寿命预测

李自林1,2邢 颖1韩庆华1,3郭 琪1

(1天津大学建筑工程学院,天津300072)(2天津城建大学天津市软土特性与工程环境重点实验室,天津300384)(3天津大学滨海土木工程结构与安全教育部重点实验室,天津300072)

基于8个组合梁试件的疲劳试验结果,采用有限元计算与名义应力法相结合的方法,提出用于模拟滑移和疲劳破坏过程的精细有限元模型和计算方法.研究了混凝土中不同橡胶掺量对组合梁极限承载力、最大滑移、栓钉应力及破坏特征的影响,得到相应的应力-疲劳寿命曲线.结果表明,简支组合梁的疲劳破坏首先发生在端部栓钉,破坏过程为栓钉依次断裂.虽然疲劳断裂为脆性破坏,但组合梁在疲劳荷载作用下的整体破坏具有一定的延性.使用弹性混凝土代替普通混凝土后,组合梁的极限承载力和刚度略有降低,但延性有所提高;当橡胶掺量为5%,10%和15%时,疲劳寿命分别提高约15%,64%和125%.基于非线性数值分析得到的组合梁极限承载力和疲劳寿命与试验所测结果吻合较好,为组合梁的抗疲劳设计提供了参考.

组合结构;数值模拟;疲劳性能;弹性混凝土;疲劳寿命;应力集中系数

弹性混凝土是在普通混凝土中掺入由汽车废弃轮胎经过机械粉碎、研磨、洗净等加工处理得到的橡胶微粒配置而成的,又称为橡胶集料混凝土[1].弹性混凝土同时具有普通混凝土强度高和橡胶变形抗裂性能好的特点,且韧性高,振动噪声小,用于组合桥面板中能增加路面耐磨性和行车舒适度.组合梁具有承载力高、刚度大、稳定性好以及施工方便等优点,其应用范围已经由桥梁结构逐步扩展到工业与民用建筑中.但组合梁的疲劳问题也日益突显,引起学者们的重视[2-6].已有研究成果表明,在疲劳荷载作用下,组合梁中栓钉首先疲劳断裂,导致抗剪承载力不足,引发疲劳破坏.目前的相关研究主要集中于普通混凝土与钢组合梁,尚缺乏对弹性混凝土与钢组合梁的探讨,对于该新型材料是否能在组合梁中发挥能量吸收好、抗裂性能强的特点并提高其疲劳性能,尚无明确的结论.基于此,本文运用有限元方法建立了计算组合梁疲劳寿命的有限元模型.在与试验结果比较和验证的基础上,分析了混凝土中不同橡胶掺量对弹性混凝土与钢组合梁疲劳性能的影响.

1 疲劳寿命预测方法

1.1 疲劳寿命计算理论

在进行疲劳寿命预测研究时,以材料的标准应力-疲劳寿命(S-N)曲线为基本依据,以有限元计算所得的理论应力集中系数为主要参数,对已有的材料S-N曲线进行修正,最终按Miner线性累计损伤理论计算并预测结构寿命.材料标准S-N曲线是利用标准尺寸的光滑试件进行疲劳寿命测试得到的;实际情况下则必须考虑构件的形状、尺寸、表面状况、平均应力及应力集中程度等因素,对S-N曲线进行修正,以用于预测疲劳寿命.

1.1.1 应力集中系数修正

材料的疲劳性能与理论应力集中系数Kt有关,应力集中越严重,则疲劳寿命越低.构件在疲劳荷载下的理论应力集中系数为[7]

(1)

式中,σm,max为构件在一定荷载下的局部最大应力,可通过有限元方法获得;σn为构件在该荷载下的名义应力.

图1为材料在不同应力集中系数下的标准S-N曲线簇.图中，σa为非对称荷载下的疲劳极限.差值计算可得任意应力集中系数下材料的S-N曲线[7].

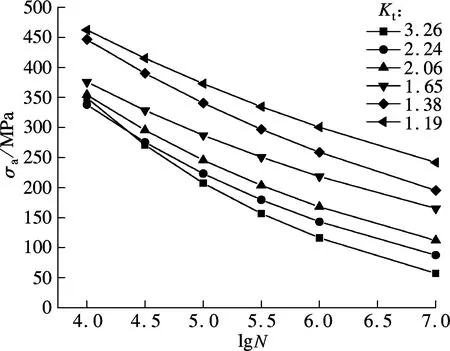
图1 Q345钢在不同应力集中系数下的S-N曲线

1.1.2 表面加工方法修正

不同钢材的疲劳性能受表面缺陷影响不同.除了钢材本身的性质外,抛光、磨光、精车、粗车、锻造等表面处理方法对疲劳寿命影响不同.钢材的表面状况对疲劳强度的影响用表面加工系数β表示,计算方法如下[7]:

(2)

式中,σ-1s为具有某种加工表面的标准光滑试件的疲劳极限;σ-11为抛光的标准光滑试件的疲劳极限.

1.1.3 平均应力修正

进行标准材料S-N曲线测试时,通常采用应力比为-1的拉压循环加载方式,即平均应力为0.研究表明,拉伸平均应力使疲劳强度和寿命降低,压缩平均应力使疲劳强度和寿命增加[7].进行实际疲劳寿命估算时,常对试件所受真实应力幅进行修正,以考虑拉伸平均应力的影响,最常用的Goodman直线模型为

(3)

式中,σ-1为对称循环下的疲劳极限;σm为平均应力;σb为抗拉强度.将修正后的σ-1作为S-N曲线中的应力幅,可得最终S-N曲线公式为

(4)

式中,a和b分别为S-N曲线在双对数坐标下的截距和斜率.由式(4)即可确定相应构件疲劳破坏时经历的循环次数(即疲劳寿命).

1.2 组合梁疲劳损伤累积方法

简支组合梁试件跨中受力最大的栓钉为疲劳危险构件.随着疲劳荷载循环次数的增加,栓钉周围的混凝土首先局部开裂,因此可采用单元“生死”的方法,将达到混凝土抗拉或抗压强度的单元“杀死”,使其退出工作[8-9].

混凝土的局部破坏使栓钉约束条件变差,受力增加.根据应力最大栓钉的受力,可由S-N曲线计算该栓钉的疲劳寿命.当加载次数达到寿命时,该栓钉承载力迅速下降,发生疲劳断裂破坏.第1根栓钉破坏,即“杀死”该单元后,剪力在剩余的栓钉内进行应力重分布,新的危险栓钉出现；当加载次数达到其计算疲劳寿命后,该栓钉也将发生疲劳断裂.随着栓钉依次疲劳破坏,有效栓钉减少；当剪跨段栓钉全部断裂后,组合作用完全丧失,试件整体强度和刚度下降,此时的疲劳加载次数即为组合梁试件的疲劳寿命.

2 有限元分析与试验对比

2.1 相关试验结果

文献[10]对缩尺组合梁构件进行了静力及疲劳试验,试件采用不完全剪力连接,构件构造见图2.由1个静力试验确定组合梁试件的极限承载力后,对7个试件施加不同的疲劳荷载幅,以获得组合梁在不同荷载下的疲劳寿命.由于疲劳试验的离散性较大,本文选取1组静力试验(编号FSCB-0)和测试结果较为理想的2组疲劳试验(编号FSCB-4,FSCB-5),利用有限元方法对其进行模拟计算并验证,试验结果见表1.

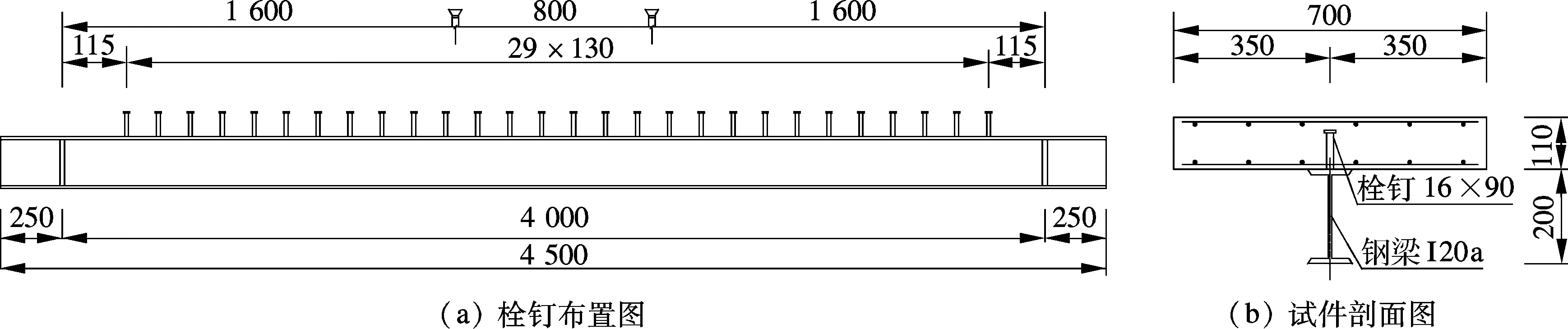
图2 试验组合梁试件构造形式(单位:mm)

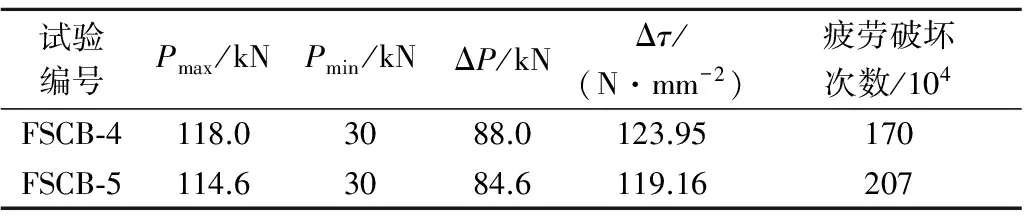
表1 钢与混凝土组合梁疲劳试验结果

注：Pmax,Pmin分别为最大、最小荷载;ΔP为荷载幅;Δτ为栓钉所受剪应力幅.

2.2 有限元计算模型

2.2.1 单元类型

组合梁试件的整体有限元模型选取对称结构的一部分.钢梁采用solid45单元,混凝土采用可考虑开裂、压碎及配筋的solid65单元.混凝土与钢梁的接触面上采用四节点3D接触单元conta173,以保证其变形时的接触关系(见图3).为了节约计算成本,栓钉采用二节点非线性弹簧单元combin39代替,以模拟其抗剪作用及钢梁与混凝土板之间的滑移性能.弹簧单元中两个端节点分别位于钢梁上表面和混凝土板下表面,这两点在位置上是重合的,具体构造见图4.但通过弹簧单元只能计算栓钉的名义剪应力,无法获得其具体应力状态,因而无法计算栓钉的应力集中系数.为此,取整体模型的典型部分,建立单根栓钉局部有限元模型(见图5).模型中混凝土板、钢梁和栓钉均采用八节点实体单元模拟,各部件表面设接触单元,根据整体模型的计算结果建立局部模型的约束条件,并施加水平剪力,以获得栓钉完全受剪时的应力状态.

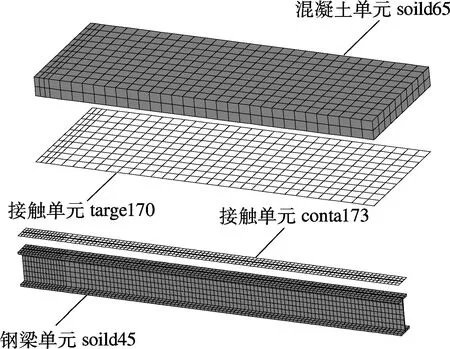
图3 整体有限元模型

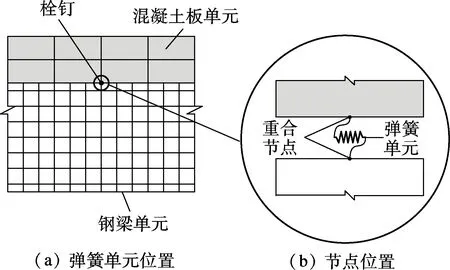
图4 整体有限元模型中栓钉形式

2.2.2 材料本构关系

试验中钢材的屈服强度为362.89 MPa,极限强度为458.03 MPa;混凝土的抗压强度为29.18 MPa,抗拉强度为2.84 MPa.分别采用文献[11]和《混凝土结构设计规范》(GB 50010—2010)提供的钢材与混凝土本构模型.

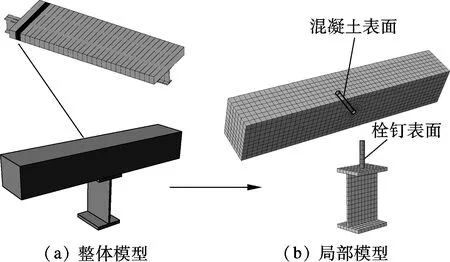
图5 有限元分析模型关系

2.2.3 混凝土板和钢梁间的相互作用

已有研究成果中得出了多种栓钉荷载-滑移模型,其中以Ollgaard等[12]提出的模型应用最为广泛,即

V=Vu(1-e-ls)m

(6)

式中,V为栓钉所受剪力;Vu为栓钉的极限承载力;s为栓钉所在位置处混凝土与钢梁的滑移量;m,l为相关系数,Ollgaard等[12]建议取m=0.588,l=1.弹簧的非线性刚度曲线可由式(6)确定.

2.3 计算结果分析

2.3.1 双重非线性分析

在组合梁跨中施加竖向位移,提取梁端支座反力，作为对称结构的极限承载力.根据有限元计算结果与静力试验可得荷载-位移曲线(见图6).由图可知,当加载至170 kN左右时,试件的整体刚度开始下降.极限承载力的试验值与计算值基本吻合,误差仅为6.1%;破坏时跨中挠度的计算值小于试验值,误差仅为3.0%.这说明有限元模型能精确模拟静力构件的受力情况,较为准确地反映构件的变形趋势.

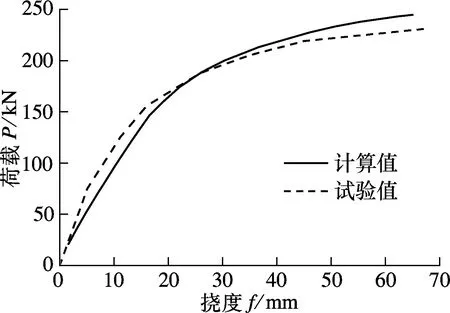
图6 组合梁跨中截面的荷载-位移曲线

组合梁试件的对称有限元模型中共有15个栓钉,由支座端至跨中编号依次为S1～S15.图7为部分栓钉的荷载-应力计算曲线.图中,τ=F/S为栓钉的名义剪应力,其中F为弹簧所受单元力,S为栓钉截面面积.

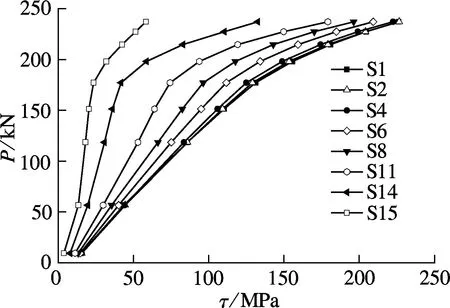
图7 栓钉的荷载-应力计算曲线

由静力有限元分析可知,支座附近栓钉S1受力最大,为疲劳破坏的危险构件,即S1将先于其他栓钉发生疲劳破坏.“杀死”S1所在单元后继续加载,计算结果显示,重分布后剩余栓钉内力显著增大,应力最大部位为支座附近的栓钉S2处.由此可见,栓钉将从支座端向跨中依次发生疲劳断裂,直至剩余栓钉过少,导致试件破坏.图8为组合梁试验中栓钉破坏照片.由图可知,圆圈所示处栓钉均被剪断,近跨中栓钉依然完好,这与计算结果一致.

图8 栓钉破坏照片[11]

2.3.2 疲劳寿命估算

对试件局部模型进行精细有限元分析,可得栓钉在某一荷载下的应力场,进而得到局部最大应力σm,max,由式(1)计算可得应力集中系数Kt.图9为计算所得的Kt-σm曲线.由图可见,加载初期应力集中系数随荷载的增大而增大;后期由于栓钉局部屈服,σm,max值等于钢材的抗拉强度,而名义应力仍随荷载不断增长,因此应力集中系数逐渐下降.实际工程中,一般结构疲劳时尚未进入塑性阶段,荷载上限不超过极限承载力的50%.由图7可知,此时危险栓钉的名义应力约为110 MPa,栓钉恰好处

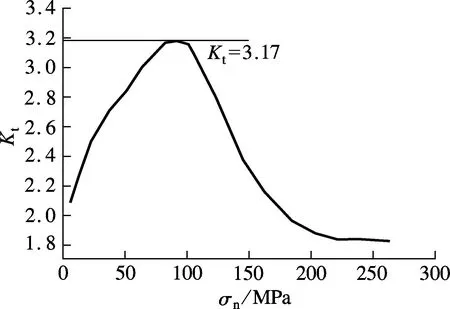
图9 栓钉应力集中系数-名义应力曲线

在应力集中系数较大的区间.选取试验结果较为理想的FSCB-4和FSCB-5两组试件进行模拟.由整体有限元分析可得栓钉所受剪应力.图10为剩余栓钉数n不同时距支座最近栓钉的荷载-应力曲线.由图可知,当疲劳荷载为30～118 kN时,τ随n的减少而增加.

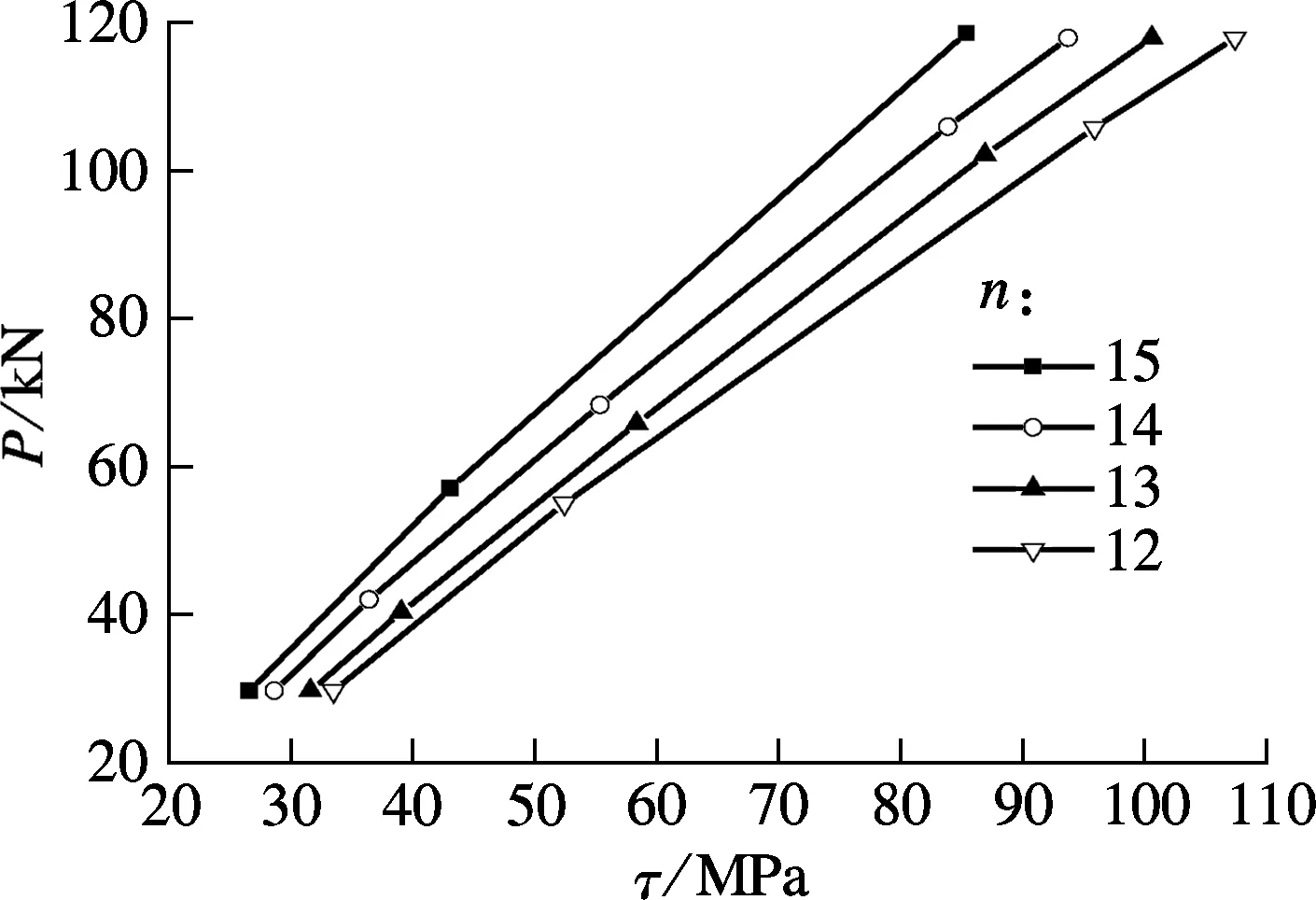
图10 危险栓钉的荷载-应力曲线

由图9及图10可得荷载为疲劳上限时不同危险栓钉的理论应力集中系数Kt,结果见表2.对于栓钉可取σ-1s=167.8 MPa,σ-11=277.2 MPa,由式(2)计算得表面加工系数β=0.773[7].根据式(4),对材料标准S-N曲线进行修正,可得危险栓钉的S-N曲线lgN=a0+b0lgσ,其中σ为疲劳应力，a0和b0为修正后参数.随剩余栓钉数量的变化,危险栓钉的位置、受力及其应力集中系数也相应改变,因此每个危险栓钉都有一条相应的S-N曲线.根据S-N曲线及Miner线性准则,计算每根栓钉成为危险栓钉后所需的加载次数,累计后得到的总加载次数即为试件在该荷载下的疲劳寿命.

试验所得2组试件的疲劳寿命分别为170×105和207×105次,有限元计算结果则分别为215.54×105和262.57×105次,误差分别为26.78%和26.84%.组合梁的疲劳强度试验值与计算值趋势吻合.

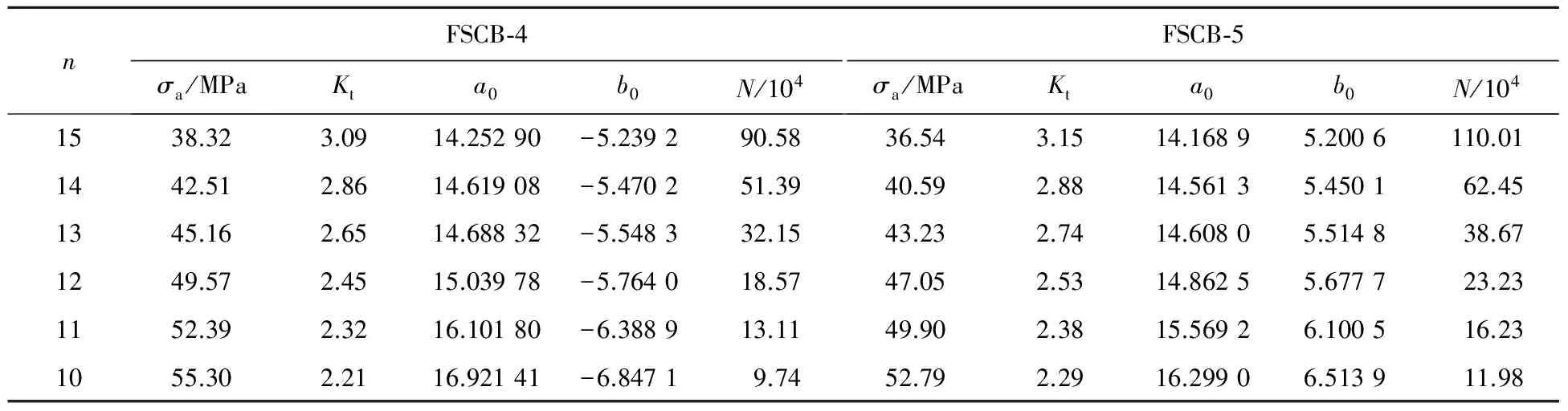
表2 疲劳寿命计算结果

3 有限元参数分析

3.1 有限元模型与弹性混凝土的本构关系

基于由试验验证的有限元模型与疲劳寿命预测方法,对含有不同橡胶掺量的弹性混凝土与钢组合梁进行参数分析.模型的尺寸和构造仍采用文献[11]中的试验构件.模型中弹性混凝土的橡胶掺量ρ=0%,5%,10%和15%,本构模型如图11所示[13].

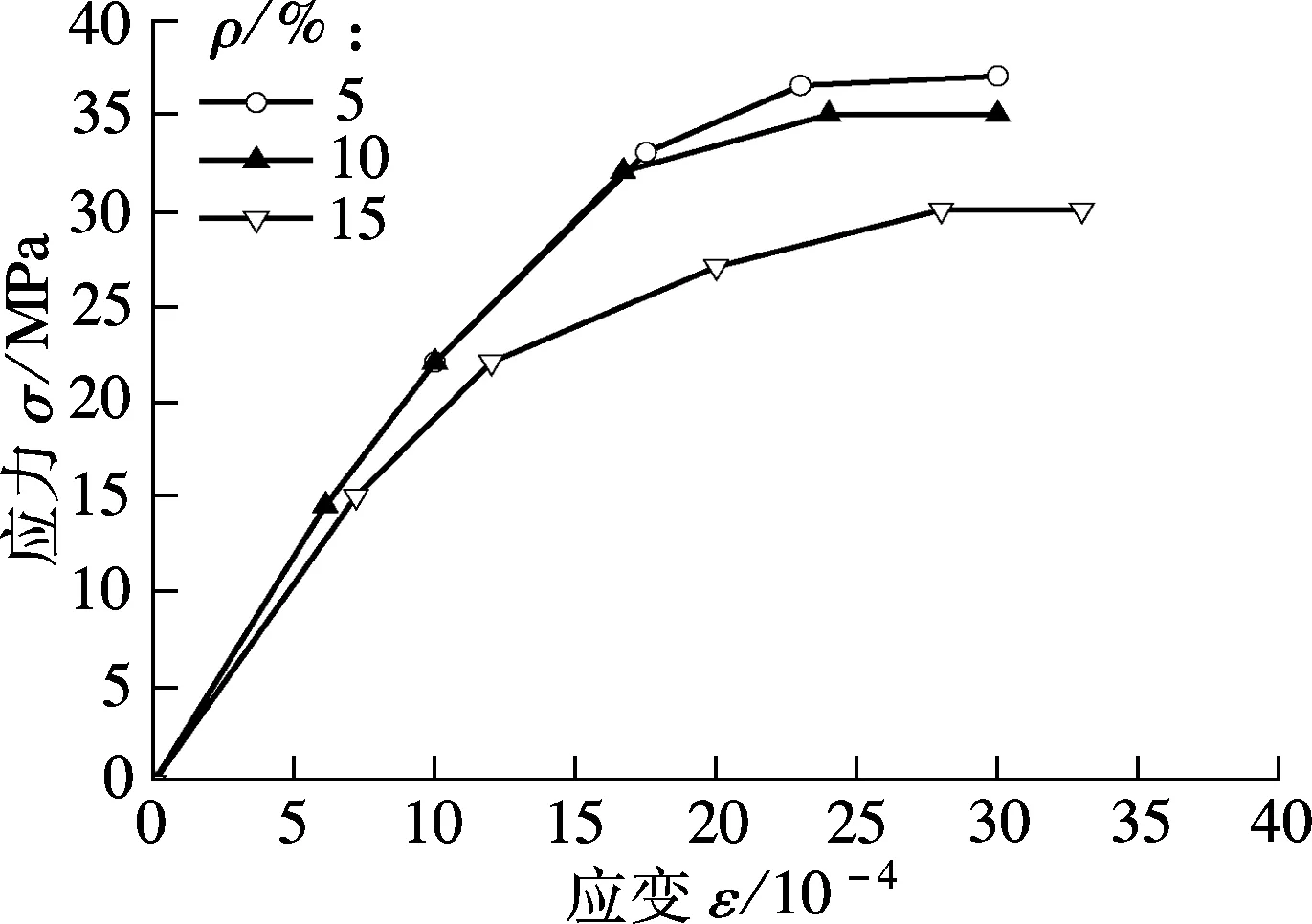
图11 不同橡胶掺量下弹性混凝土的应力-应变曲线

3.2 参数化分析结果

3.2.1 荷载-位移曲线

在组合梁跨中施加竖向位移荷载,荷载-位移曲线如图12所示.由于弹性混凝土的弹性模量和抗压强度比普通混凝土低,因此随着橡胶集料掺量的增加,试件的刚度和强度都略有下降.当橡胶掺量ρ=5%,10%和15%时,极限承载力分别下降约4.5%,9.1%和13.5%.

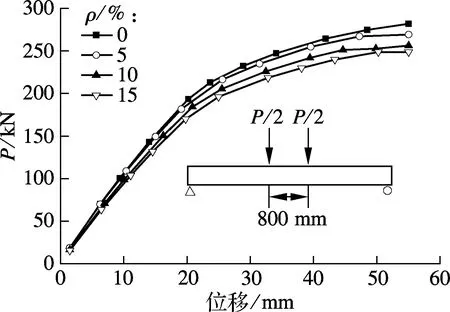
图12 不同橡胶掺量下组合梁的荷载-位移曲线

3.2.2 荷载-滑移曲线

组合梁在跨中滑移最小,支座端滑移最大.图13为不同橡胶集料掺量下组合梁试件在滑移最大截面处的荷载-滑移曲线.计算结果表明,滑移与荷载呈非线性关系,考虑混凝土和钢梁的自然黏结作用,前期滑移发展缓慢,后期滑移则发展加快,这主要是由于后期试件急剧增大的弯曲变形所引起的.随着混凝土中橡胶掺量的增加,相同荷载下的滑移量有所增加;造成这一现象的主要原因是,橡胶集料的增加使弹性混凝土的变形能力增大,试件展现出更好的延性.

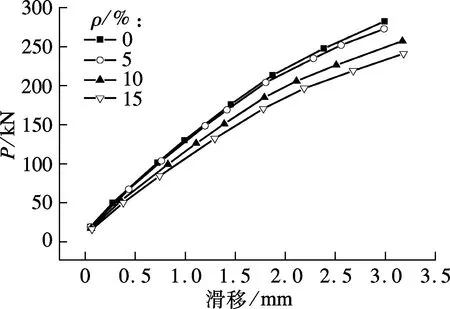
图13 不同橡胶掺量下组合梁的荷载-滑移曲线

3.2.3 疲劳寿命计算

对4组不同橡胶掺量下弹性混凝土组合试件施加30～118 kN的疲劳荷载,栓钉的应力集中系数如图14所示.由图可见，增加橡胶颗粒掺量后,栓钉根部的应力集中情况明显减弱.根据应力集中系数对材料S-N曲线进行修正，可得每个栓钉的S-N曲线,计算所得的疲劳寿命见表3.由表可知,第1根栓钉破坏所经历的加载循环次数最多,占总寿命的40%.当发生第1次局部疲劳断裂后,试件仍具有静力承载力及一定的疲劳承载力.剩余栓钉数量越少,试件受力越大,寿命越小.当剩余栓钉数小于11时,试件可承受的疲劳循环次数已经很小,对总寿命的贡献可忽略不计,因此认为当第5根栓钉断裂后,剩余栓钉相继剪断,最终发生疲劳破坏.

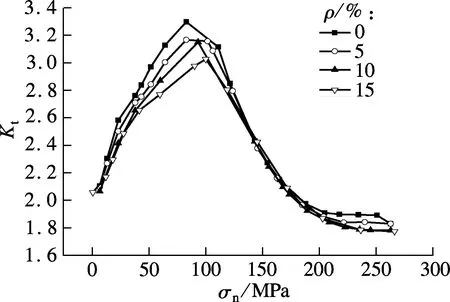
图14 不同橡胶掺量下组合梁中栓钉的应力集中系数曲线

表3 不同橡胶掺量下组合梁的疲劳寿命计算

注：σmin,σmax分别为疲劳应力的上限和下限.

由图14可知,当疲劳荷载相同时,在橡胶掺量较大的试件中,栓钉应力集中系数较小,则受力更均匀,因此单根栓钉及整体试件的疲劳寿命均增大.由表3计算得到，当ρ=0%,5%,10%和15%时,疲劳寿命分别为208.41×105,240.55×105,343.59×105和469.01×105次,弹性混凝土试件的疲劳寿命较普通混凝土分别增大约15%,64%和125%.综合考虑承载力、刚度和抗疲劳性的要求,橡胶掺量为5%和10%的弹性混凝土在承受疲劳荷载的构件中有较大应用价值.

4 结论

1) 有限元计算分析表明,组合梁在危险栓钉处首先发生疲劳断裂,但危险栓钉断裂后构件仍具有静力承载力和疲劳承载力.这表明组合梁具有良好的应力重分布能力和一定的延性,能有效避免脆性疲劳断裂造成的突然破坏.

2) 使用有限元数值模拟与名义应力法相结合的方法,能够推导出适用于具体构件的修正S-N曲线,计算结果与试验吻合良好,该方法具有一定的可行性.但计算过程没有考虑焊接缺陷,仿真结果可作为概率意义上的参考.

3) 弹性混凝土与钢组合梁较普通组合梁极限承载力有所降低.随着橡胶掺量的增加,整体刚度和强度下降程度增加;当橡胶掺量达到15%时,组合梁极限承载力降低约13.5%.

4) 弹性混凝土能显著改善组合梁的抗疲劳性能,橡胶掺量越大,抗疲劳性能提高越明显.综合考虑承载力、刚度和抗疲劳性的要求,橡胶掺量为5%和10%的弹性混凝土在承受疲劳荷载的构件中有较大应用价值.

References)

[1]Liu F, Chen G, Li L, et al. Study of impact performance of rubber reinforced concrete[J].ConstructionandBuildingMaterials, 2012, 36: 604-611.

[2]聂建国, 王宇航. 钢-混凝土组合梁疲劳性能研究综述[J]. 工程力学, 2012, 29(6):1-11. Nie Jianguo, Wang Yuhang. Research status on fatigue behavior of steel-concrete composite beams[J].EngineeringMechanics, 2012, 29(6):1-11. (in Chinese)

[3]卫星, 李小珍, 李俊, 等. 钢箱梁斜拉桥锚拉板式索梁锚固结构的试验研究[J]. 工程力学, 2007,24(4):135-141. Wei Xing, Li Xiaozhen, Li Jun, et al. Experimental study on anchor-plate anchorage for cable-stayed bridges with steel box girder[J].EngineeringMechanics, 2007,24(4):135-141. (in Chinese)

[4]Lee P G, Shim C S, Chang S P. Static and fatigue behavior of large stud shear connector for steel-concrete composite bridges[J].JournalofConstructionalSteelResearch, 2005, 61(9): 1270-1285.

[5]Hanswille G, Porsch M, Ustundag C. Resistance of headed studs subjected to fatigue loading: part Ⅰ: experimental study[J].JournalofConstructionalSteelResearch, 2007, 63(4): 475-484.

[6]Badie S S, Morgan Girgis A F, Tadros M K, et al. Full-scale testing for composite slab/beam systems made with extended stud spacing[J].JournalofBridgeEngineering, 2011, 16(5): 653-661

[7]赵少汴,王忠保. 抗疲劳设计——方法与数据[M]. 北京:机械工业出版社,1997:35-36.

[8]Nguyen H T, Kim S E. Finite element modeling of push-out tests for large stud shear connectors [J].JournalofConstructionalSteelResearch, 2009, 65(10): 1909-1920.

[9]姜绍飞, 王鹏, 吴兆旗. 钢-混凝土组合梁疲劳性能的有限元分析[J]. 沈阳建筑大学学报, 2009, 25(1): 112-115. Jiang Shaofei, Wang Peng, Wu Zhaoqi. Finite element analysis on fatigue behavior of steel-concrete composite beams[J].JournalofShenyangConstructionUniversity, 2009, 25(1):112-115. (in Chinese)

[10]Wang Y H, Nie J G, Li J J. Study on fatigue property of steel-concrete composite beams and studs[J].JournalofConstructionalSteelResearch, 2014, 94: 1-10.

[11]张莉. 钢结构刚性梁柱节点抗震性能的研究[D]. 天津:天津大学建筑工程学院,2004.

[12]Ollgaard J G，Slutter R G, Fisher J W. Shear strength of stud connectors in lightweight and normal weight concrete[J].AISCEngineeringJournal, 1971, 8(2): 55-64.

[13]王庆余. 橡胶集料混钢筋混凝土叠合梁受弯性能有限元分析[D]. 天津:天津大学建筑工程学院,2007.

Fatigue behavior analysis and life prediction of elastic concrete and steel composite beam

Li Zilin1,2Xing Ying1Han Qinghua1,3Guo Qi1

(1School of Civil Engineering, Tianjin University,Tianjin 300072, China) (2Tianjin Key Laboratory of Soft Soil Characteristics and Engineering Environment, Tianjin Institute of Urban Construction,Tianjin 300384,China) (3Key Laboratory of Coast Civil Structure Safety of Ministry of Education, Tianjin University, Tianjin 300072, China)

Based on the results of fatigue experiments of eight composite beams, a fine finite element model and a calculation method applied for simulating slip and fatigue failure process are proposed by using the method combining finite element calculation with nominal stress approach. The effects of the different rubber contents in concrete on the ultimate bearing capacity, maximum slip, stress of stud and failure characteristics of composite beams are studied, and the corresponding stress-fatigue life curves are obtained. The results show that fatigue failure of simply supported composite beam first occurs at the end stud, and spreads in proper order. Although fatigue break is brittle failure, the general demolition of composite beams under fatigue loads has some ductility. After replacing normal concrete by elastic concrete, the ultimate bearing capacity and stiffness of composite beams decreases slightly while the ductility increases. The fatigue life increases by about 15%, 64% and 125% when the volumetric fractions of rubber are 5%, 10% and 15%, respectively. The ultimate bearing capacity and fatigue life evaluated by nonlinear numerical analysis agree well with those obtained by the fatigue tests, providing valuable references for the fatigue resistant design of composite beams.

composite structure; numerical simulation; fatigue behavior; elastic concrete; fatigue life; stress concentration factor

2014-06-18. 作者简介: 李自林(1953—),男,教授,博士生导师;韩庆华(联系人),男,博士，教授,博士生导师,qhhan@tju.edu.cn.

国家自然科学基金资助项目(51178307,51408408)、天津市自然科学基金资助项目(13JCBJC19600).

李自林，邢颖，韩庆华，等.弹性混凝土与钢组合梁的疲劳性能分析及寿命预测[J].东南大学学报:自然科学版,2015,45(1):165-171.

10.3969/j.issn.1001-0505.2015.01.029

TU398

A

1001-0505(2015)01-0165-07