混凝土结构多尺度建模界面连接方法

张 莹 孙广俊 李鸿晶

(南京工业大学土木工程学院, 南京 210009)

混凝土结构多尺度建模界面连接方法

张 莹 孙广俊 李鸿晶

(南京工业大学土木工程学院, 南京 210009)

分别采用变形协调方法和力的平衡方法建立了混凝土单柱的多尺度模型,分析了混凝土柱在静力荷载下的内力分布特征及动力荷载下的变形性能,并对多尺度模型界面连接方式的合理性进行了分析.在此基础上,以某三层钢筋混凝土框架结构为例,分别建立了结构的实体模型、梁模型和力平衡界面连接下的多尺度模型;计算了多尺度模型的低周往复性能,并与试验结果进行对比,以验证力平衡界面连接方式在多尺度建模中的有效性.结果表明:在静力荷载作用下,运用力平衡方法处理界面连接较变形协调方法更符合实际受力情况;在动力荷载作用下,2种界面连接方式都是可行的.采用多尺度模型进行整体结构建模,既能可靠地实现结构整体受力行为的模拟,还能反映结构关键部位的受力性能,计算效率显著提高.

混凝土结构; 多尺度模型; 变形协调; 力的平衡; 界面连接

随着有限元技术的发展,工程计算的准确性和高效性越来越受到重视．常用的计算类型包括基于杆系、壳单元等宏观模型的整体结构非线性计算和基于实体单元的微观模型精细化分析[1]．宏观模型计算效率较高,但不能反映结构局部损伤的发展过程和破坏机理．微观模型虽然可以较好地模拟结构的局部破坏过程,但却受到计算能力的限制．从整体结构中取出局部构件进行精细分析,则难以准确模拟其边界条件．多尺度模型既能有效控制计算量,又能准确反映结构局部损伤过程,适用于复杂荷载下大型结构的精细化模拟．

近年来,国内外研究人员对多尺度模型进行了研究探索和实践,为结构损伤分析提供了有效的模拟方法[2-11]．林旭川等[1]对结构的梁柱、节点以及整体框架进行了多尺度模拟,研究了结构地震响应的倒塌过程．Hund等[4]采用变分多尺度方法进行结构损伤分析．陈志文等[5-8]进行了大跨桥梁结构的多尺度模拟和节点损伤分析．石永久等[9]对多尺度界面连接方法进行了理论分析,指出梁单元与实体单元、梁单元与壳单元以及壳单元与实体单元的连接原理基本相同,并建立了钢框架模型进行验证．然而,由于不同尺度单元的结点自由度和精度不同,计算时单元之间的界面连接需要根据变形协调方法或力的平衡方法进行处理,使之既不损失宏观模型的自由度,也不增加微观模型的额外约束．如何实现模型单元在不同尺度之间的过渡是一个亟待解决的问题．

本文分别采用变形协调方法和力的平衡方法建立了混凝土柱的多尺度有限元模型,并进行了对比分析．在此基础上,以一钢筋混凝土框架结构为例,验证了力平衡界面连接方式在多尺度建模中的准确性及多尺度模型的高效性．

1 界面连接方式

目前,工程结构中不同尺度单元间的连接情况包括以下3种:① 梁单元与实体单元的连接;② 梁单元与壳单元的连接;③ 壳单元与实体单元的连接．不同尺度模型单元之间的连接原理基本相同,故本文以梁单元-实体单元的连接为例,说明连接处理的基本原理和方法．

1.1 基于变形协调方法的界面连接

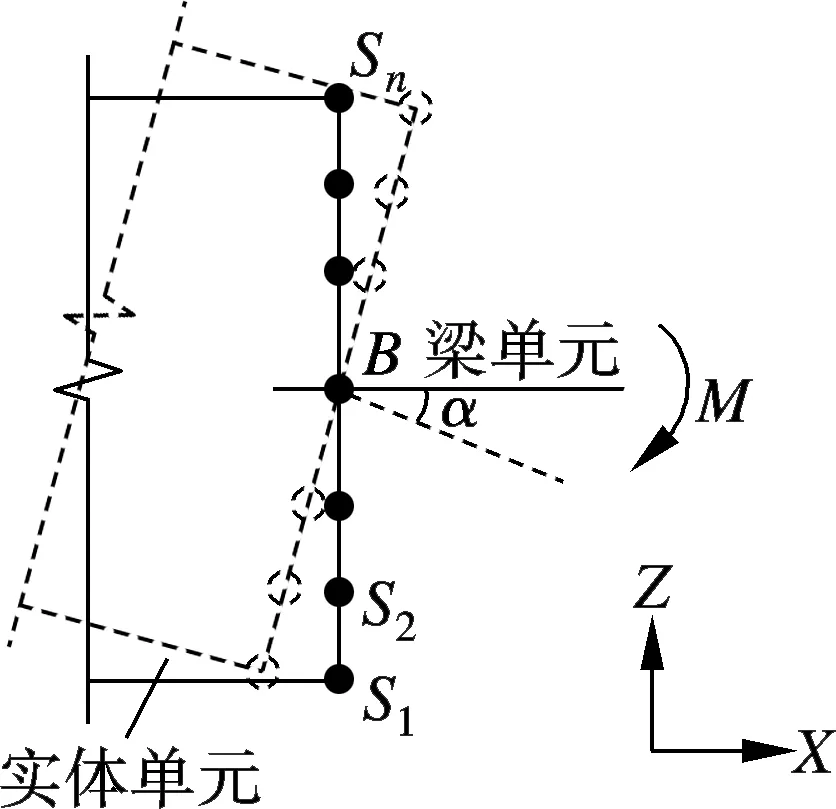
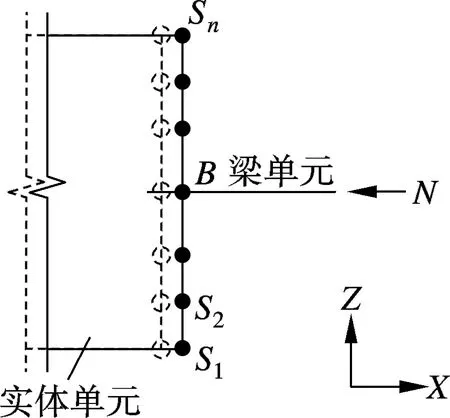
图1为梁单元与实体单元分别在弯矩和轴力作用下节点位移协调的示意图．图中,Si(i=1,2,…,n)为实体单元节点；B为梁单元节点；α为Y轴方向转角;M为弯矩;N为轴力．显然,梁单元节点B和实体单元节点Si的位移耦合．

当梁单元主动变形时,实体单元界面上节点Si的位移可由梁单元节点B的位移决定,即

Δxsi=ΔxB+rsisinα

(1)

(a) 弯矩作用

(b) 轴力作用

Δzsi=ΔzB+rsi(cosα-1)

(2)

式中，Δxsi,Δzsi分别为实体单元节点Si的X轴和Z轴轴向位移; ΔxB, ΔzB分别为梁单元节点B的X轴和Z轴轴向位移;rsi=zsi-zB,其中zsi和zB分别为实体单元节点和梁单元节点的Z轴坐标．

当实体单元主动变形时,梁单元节点B的位移可由实体单元界面上的所有节点决定,即

(3)

(4)

(5)

式中,h为Z轴方向上的实体单元高度.

1.2 基于力平衡方法的界面连接

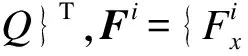
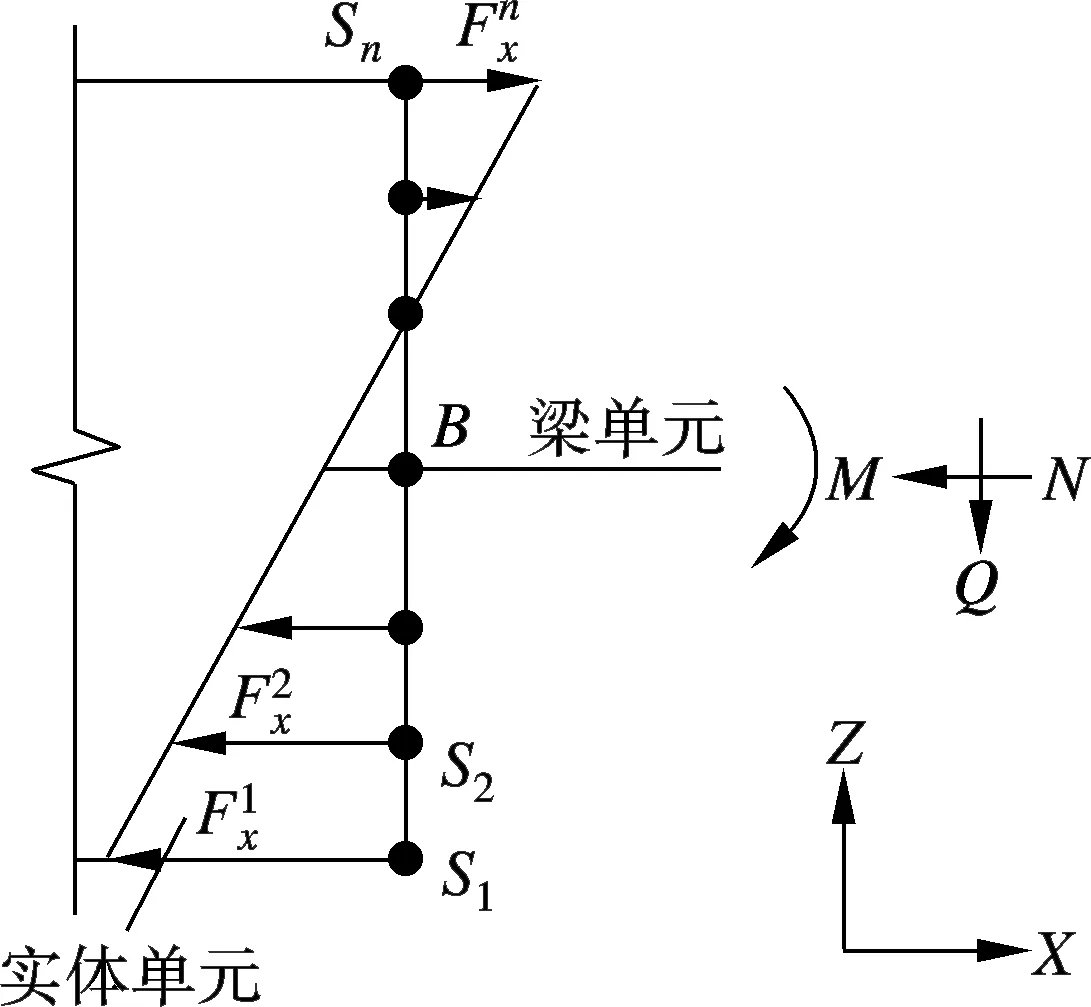
图2 节点反力关系示意图

当梁单元主动变形时,实体单元界面上节点Si的内力可以由梁单元节点B的内力决定,即

(6)

(7)

当实体单元主动变形时,梁单元节点B的内力可以由实体单元界面上的所有节点决定,即

(8)

(9)

(10)

式中,A为实体单元截面面积;Ai为实体单元节点Si的影响面积;I为实体单元截面形心轴方向的惯性矩．

2 不同界面连接方法比较

为了比较多尺度建模时2种不同界面连接方法的差异，利用有限元软件ABAQUS,实现了不同尺度单元的连接．以一个边长为0.2 m、长为2 m、底部固定、顶部自由的正方形混凝土柱加载算例来验证界面连接方法的有效性．材料的弹性模量为30 GPa,泊松比为0.2,建立的有限元模型如图3所示．图中,模型A全部采用实体单元;多尺度模型B1,B2,B3中,一段采用实体单元,另一段采用纤维梁单元,分别运用变形协调方法和力的平衡方法进行多尺度连接,这3个模型的差别在于多尺度界面位置不同;模型C全部采用梁单元．

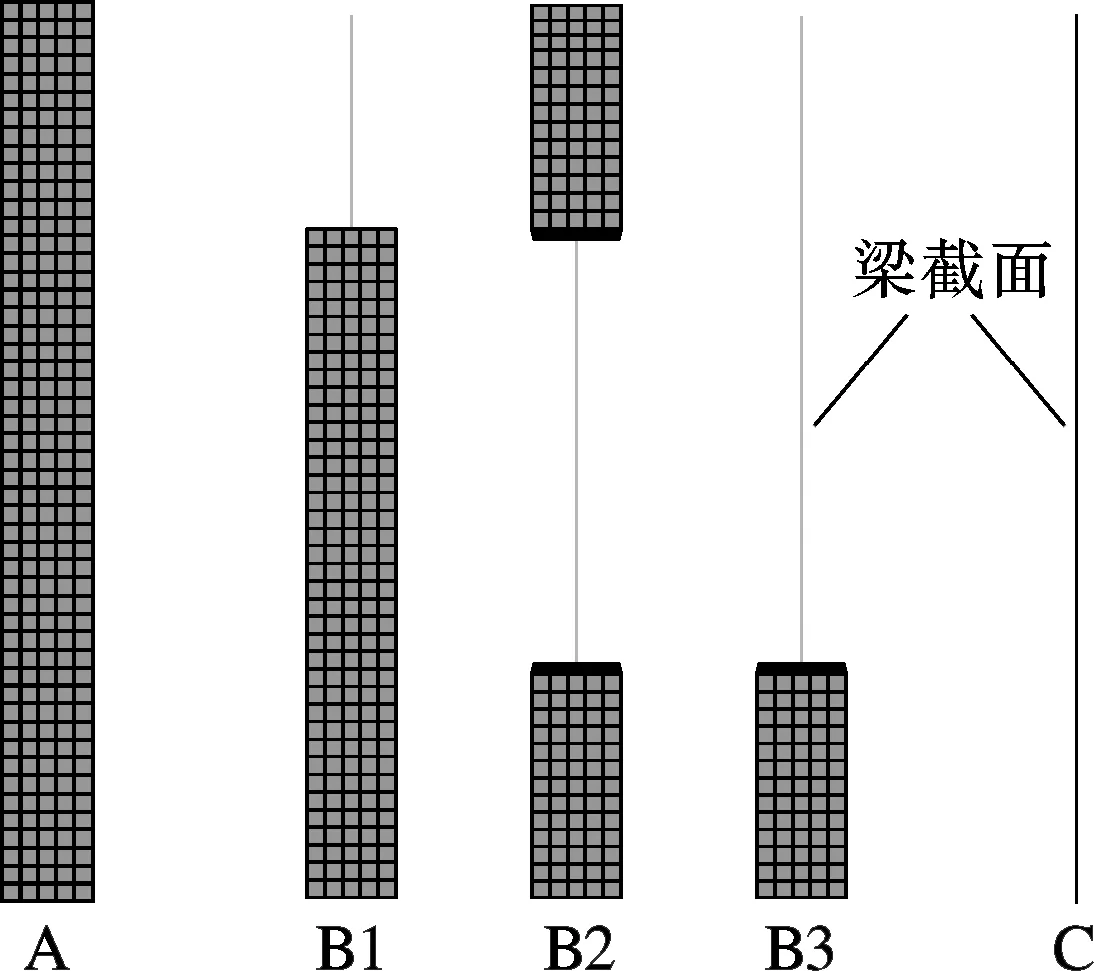
图3 柱的有限元模型

2.1 静力荷载作用

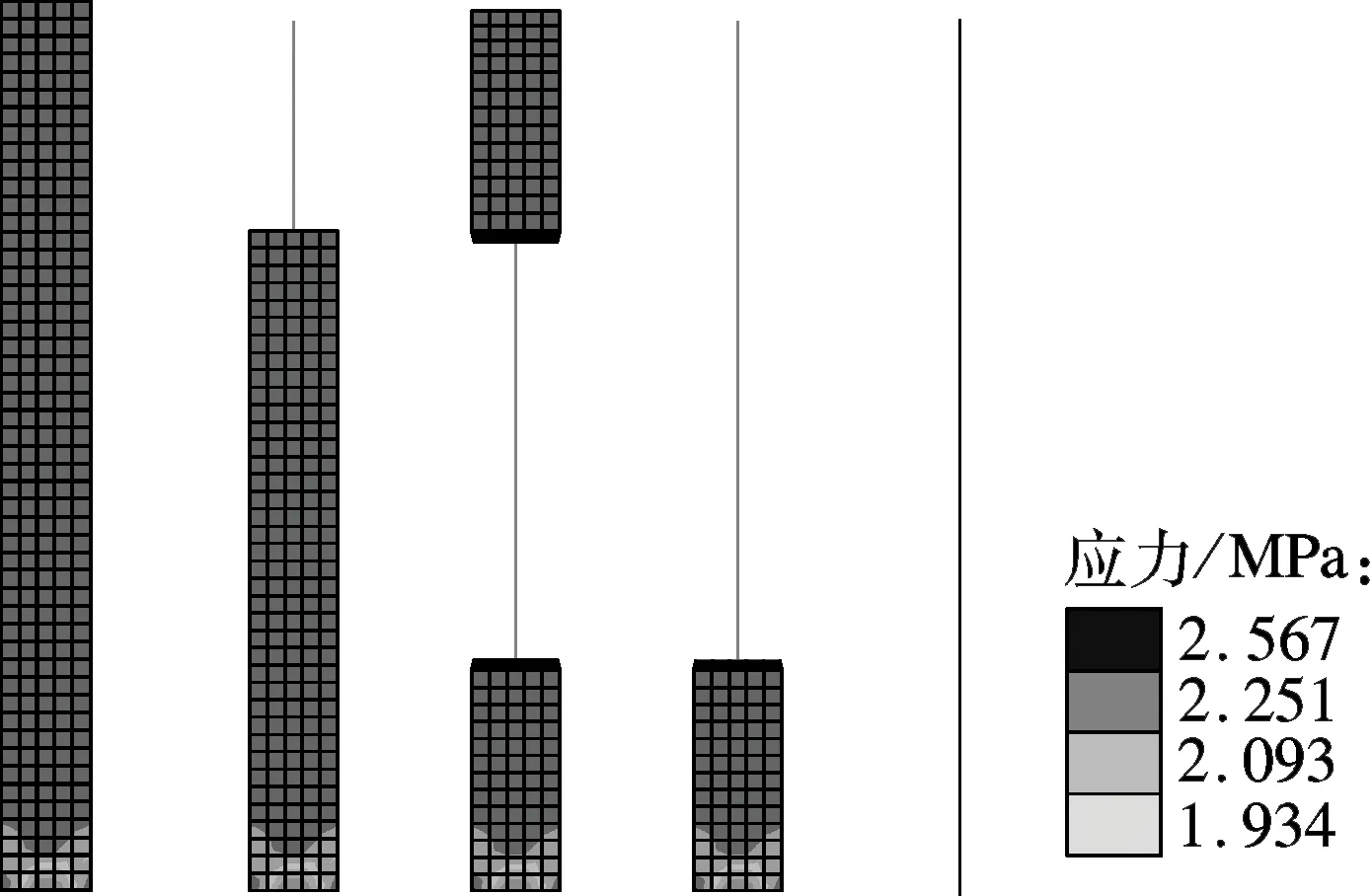
在模型顶端分别施加1 000 kN的剪力和100 kN的轴力,其应力分布结果分别见图4和图5．

由图4可以看出,施加剪力时,无论是运用变形协调方法还是力的平衡方法处理连接的模型,5个构件的变形和应力云图均一致,且界面区域未出现应力集中问题．这说明界面单元连接实现了变形协调,完成了不同单元连接之间力的有效传递．

(a) 变形协调方法

(b) 力的平衡方法

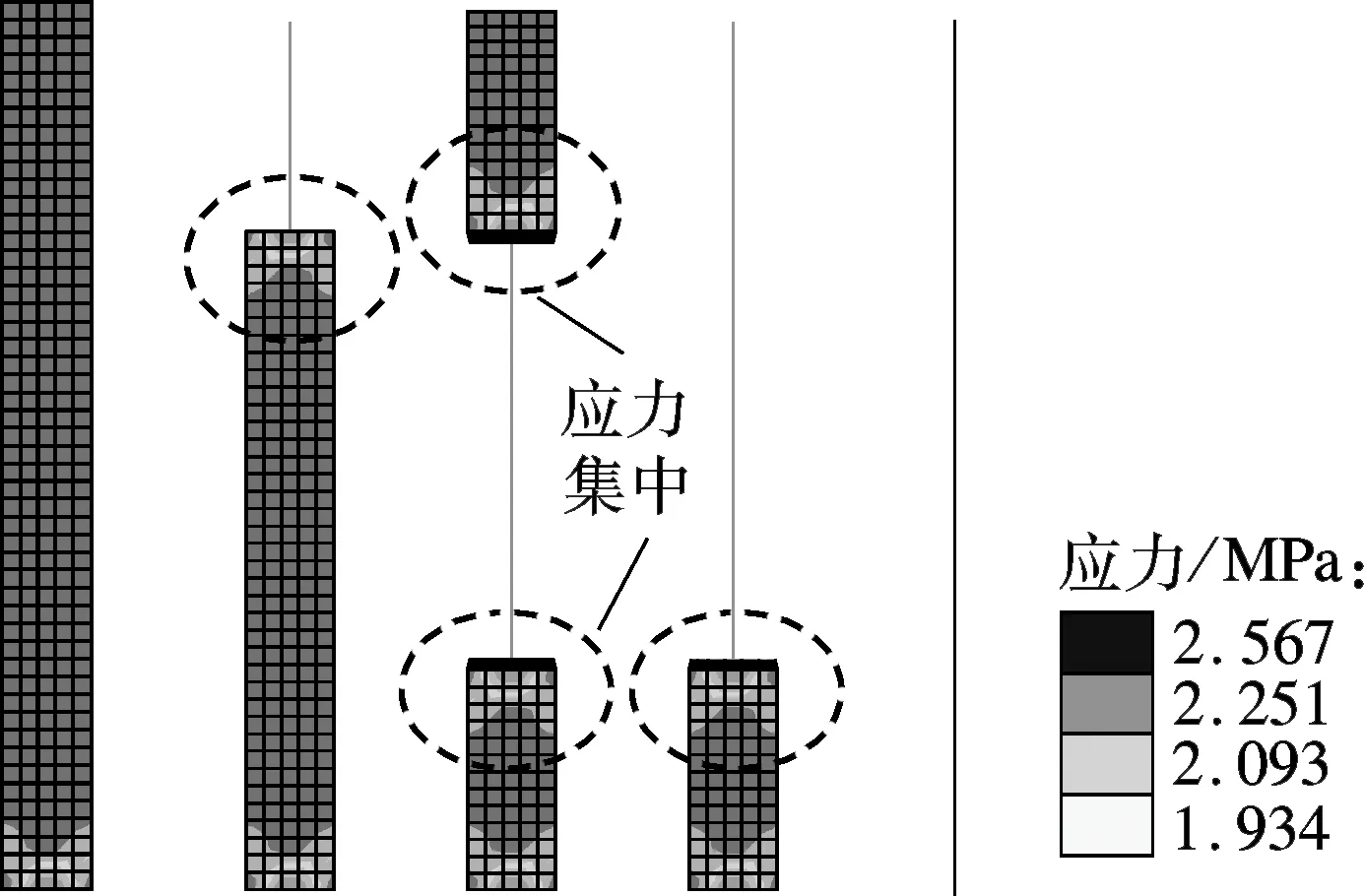
(a) 变形协调方法

(b) 力的平衡方法

由图5可知,施加轴力时,运用力的平衡方法处理连接的模型,其变形和应力云图均一致．而运用变形协调方法处理连接时,中间3个多尺度模型与完全是实体单元模型的应力变化不一致,界面区域与柱底固结区域都出现了应力分布不均匀的现象．这是因为受泊松效应影响,实体单元界面上节点受到了约束．由于梁单元是一维模型,在对称轴力作用下,节点B垂直于梁轴线方向的位移为0,由式(2)可知,实体单元界面上的节点Si的相应位移也为0,即在施加荷载的过程中,梁单元模型无法反应出构件轴向力对其他2个方向的影响．

2.2 动力荷载作用

选用1940年El Centro波(NS)的峰值段,对图3中的5个模型施加地面运动加速度时程．

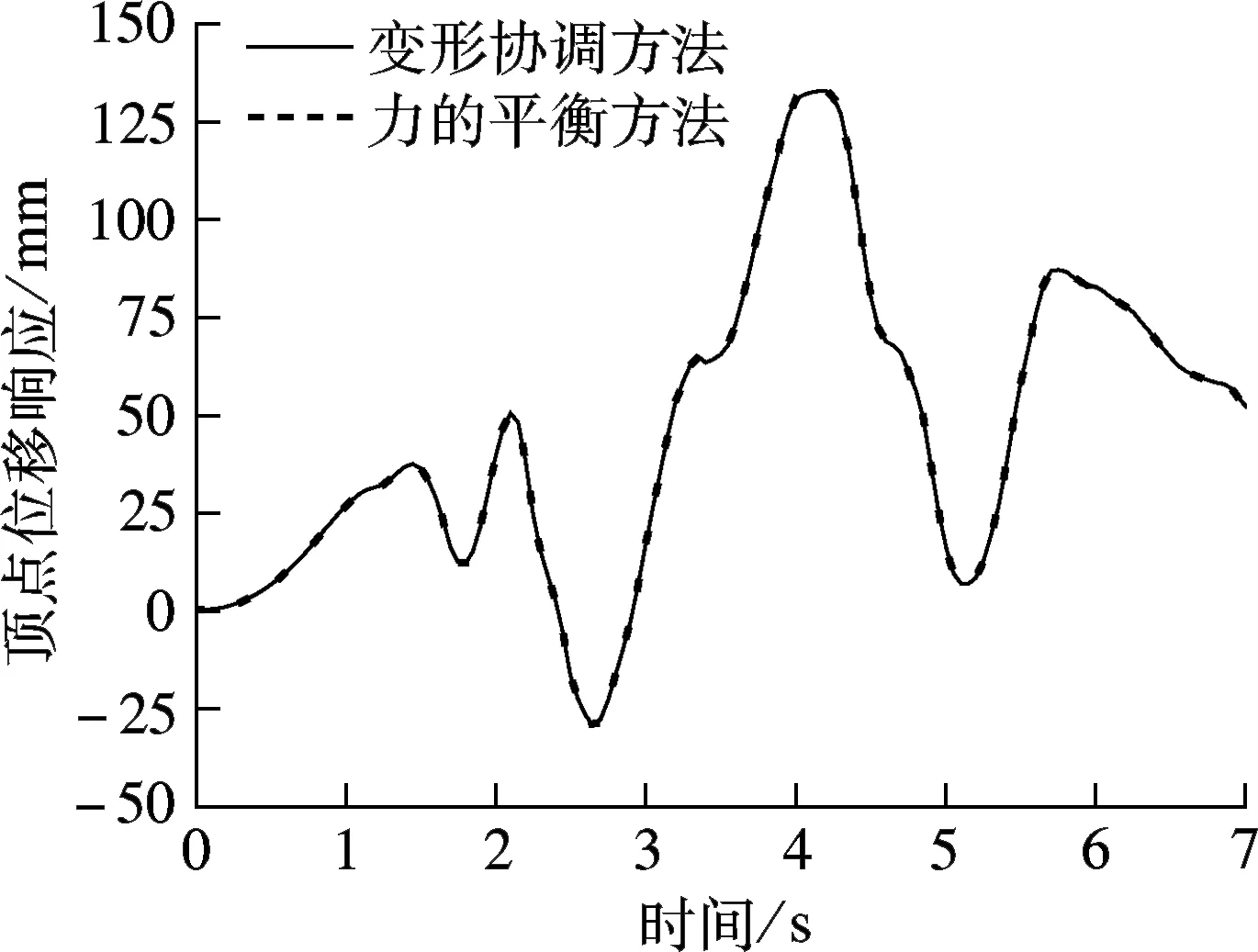
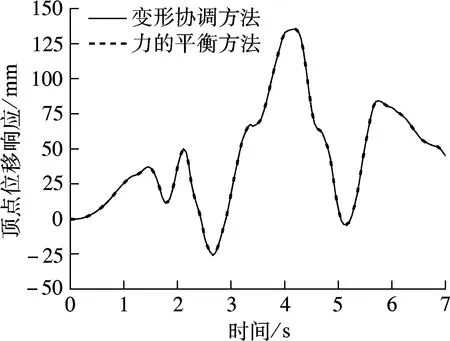
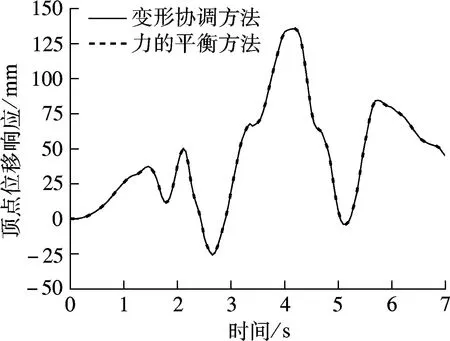
图6为模型B1,B2,B3的柱顶位移时程曲线．由图可知,2种界面连接方法的计算结果一致．图7为5个模型的柱顶位移时程曲线比较．由图可知,在地震荷载前段,5个模型的位移时程曲线一致,在后段则存在明显差异．究其原因在于:模型进入弹塑性阶段后,梁单元和实体单元判别材料的塑性准则有所不同;不同单元尺度本身就存在一定的动力特性差异;由于梁单元是一维模型,施加荷载时,梁单元模型无法反映出构件对其他2个方向的影响,且忽略了受力过程中柱底部的局部屈曲．

(a) 模型B1

(b) 模型B2

(c) 模型B3

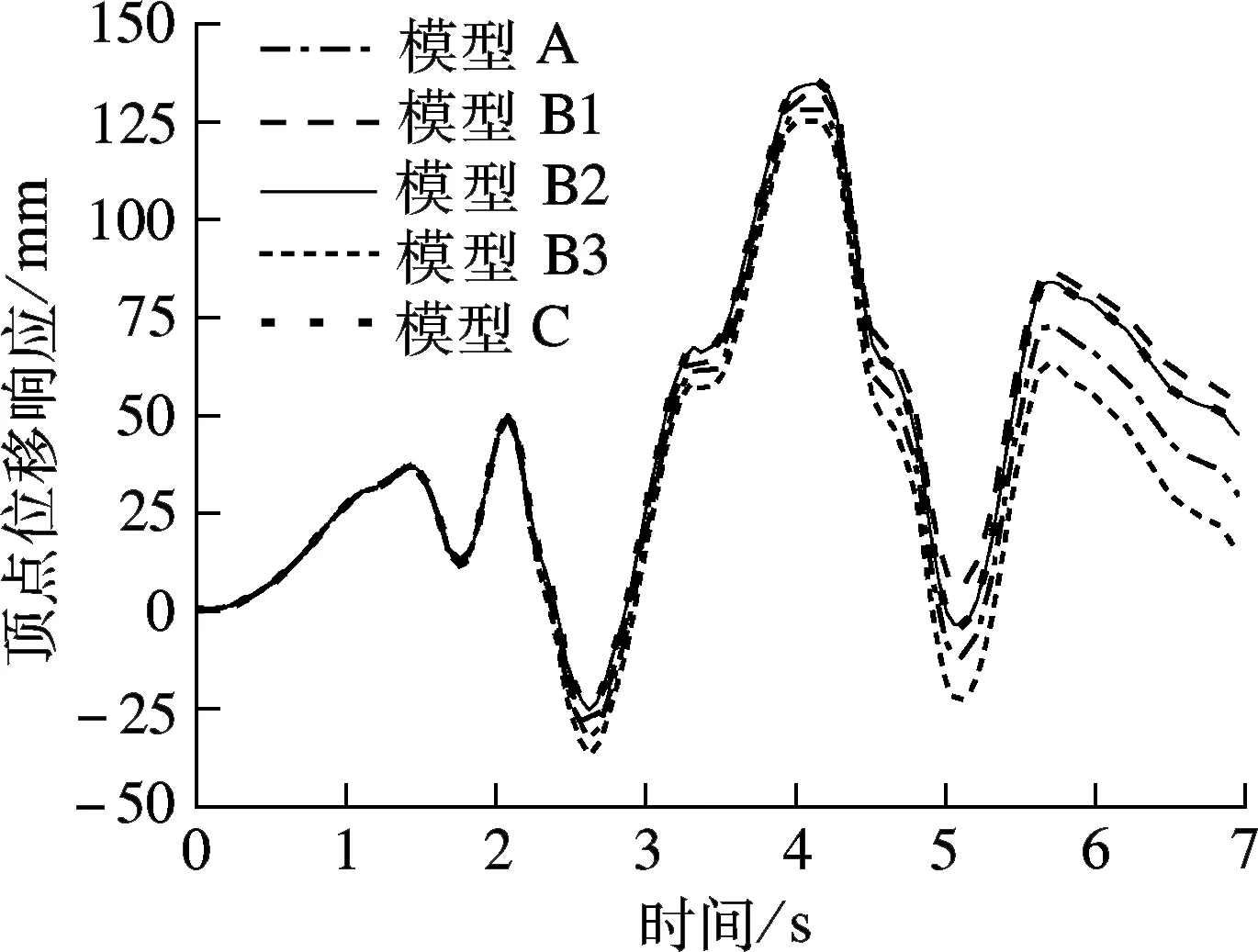
图7 5个模型的柱顶位移时程曲线比较

综上所述,在静力荷载作用下,运用力的平衡方法处理界面连接较变形协调方法更为准确;而在动力荷载作用下,2种界面连接方法都是可行的．运用力的平衡连接方法能够实现单元不同尺度间的过渡,从而可将精细模型植入整个宏观梁单元模型结构中．

3 结构多尺度模型分析及验证

本文对文献[12]中的钢筋混凝土框架结构拟静力倒塌试验进行数值模拟,以验证多尺度模型及力的平衡连接方法在结构模拟分析中的有效性．

3.1 实验概况

框架的简化示意图见图8．框架底部固定,在底层柱脚设计了拉梁．拉梁距基底0.75 m,其余3层每层高1.65 m,每跨长3 m,梁、柱构件的详细尺寸见图9．分别在边柱和中柱的柱顶施加固定竖向力N1=163 kN,N2=326 kN．每一层梁端按比例递增方式施加水平循环位移荷载D．

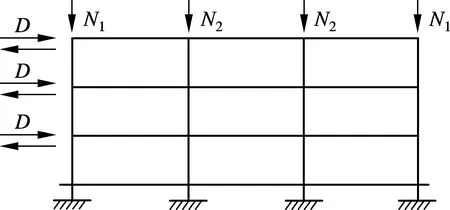
图8 框架简化示意图

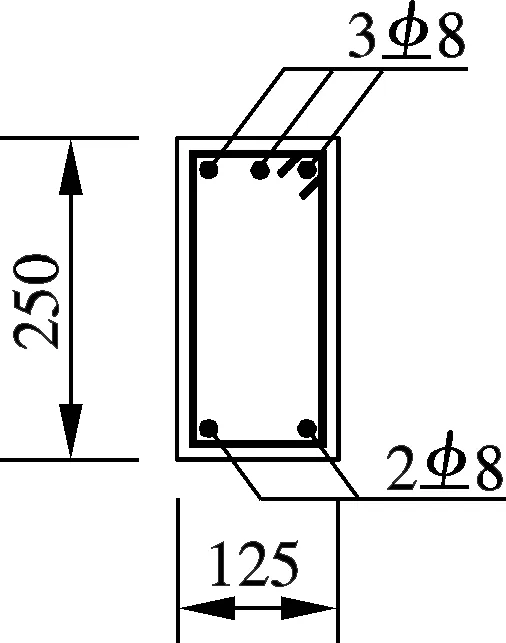
(a) 梁

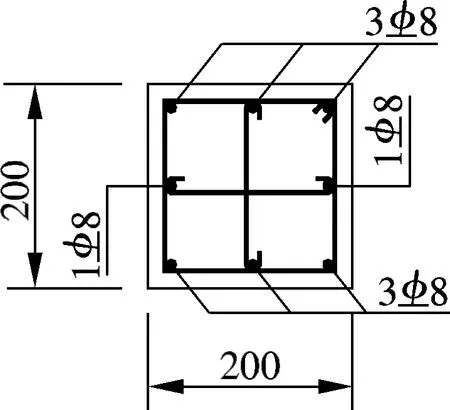
(b) 柱

整个试验过程中,正向加载时,从左往右第3根柱破坏较为严重;反向加载时,从左往右第2根柱破坏较为严重[13]．试验框架柱底塑性铰区主要位于基础拉梁以上,且中柱的拉梁层柱脚混凝土剥落,钢筋屈曲(见图10)．

(a) 整体框架变形

(b) 柱脚破坏

3.2 有限元模型的建立

通过有限元软件ABAQUS,分别建立了3种类型的结构有限元模型:宏观梁模型、多尺度模型和细观实体模型(见图11)．由于结构节点处是易损区域,故在多尺度模型中,将节点作为损伤的关键部位建立实体模型,其他部分则采用宏观尺度的梁单元,运用力的平衡方法处理2种不同尺度单元的连接．实体部分采用分离式模型;混凝土本构采用Lubliner等[14]提出的损伤塑性模型;钢筋本构采用强化的双折线模型,不考虑刚度的退化．

3.3 动力特性分析

(a) 宏观梁模型

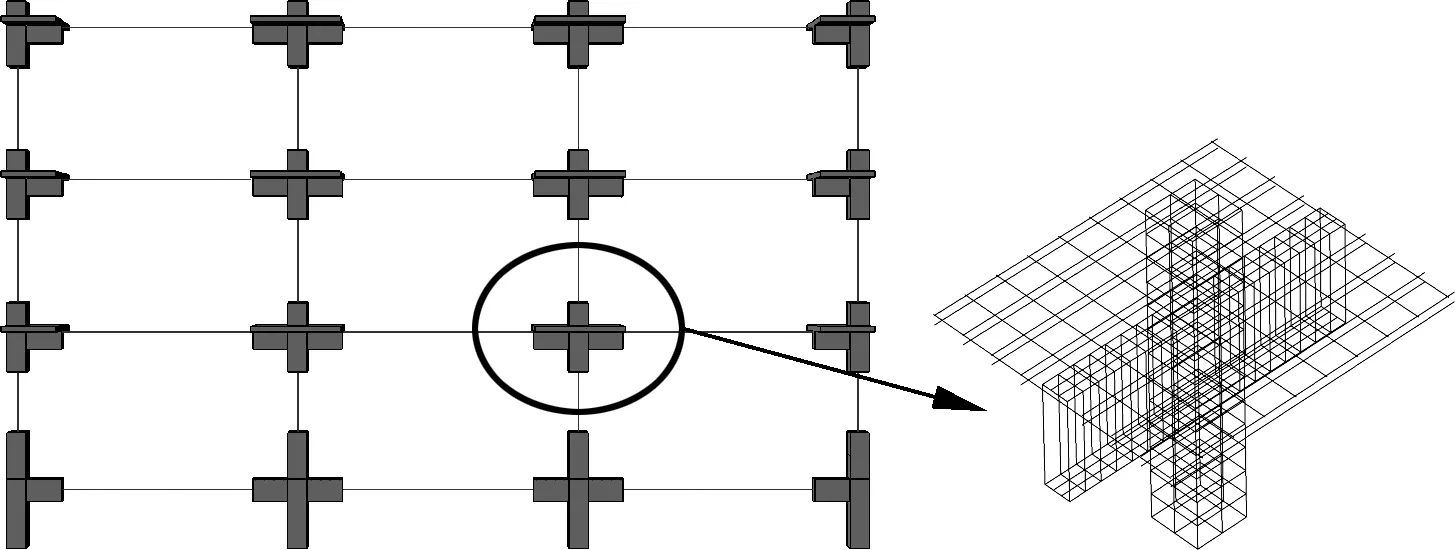
(b) 多尺度模型

(c) 细观实体模型

宏观梁模型、多尺度模型、细观实体模型的前3阶振型如图12所示,相应的自振频率见表1．可以看出,3种模型的振型一致,且计算得到的频率值相差不大,其差异主要来源于梁单元和实体单元本身存在的动力特性差异．这说明运用多尺度有限元模型进行整体动力特性分析是有效可行的．

(a) 宏观梁模型的第1阶振型

(b) 多尺度模型的第1阶振型

(c) 细观实体模型的第1阶振型

(d) 宏观梁模型的第2阶振型

(e) 多尺度模型的第2阶振型

(f) 细观实体模型的第2阶振型

(g) 宏观梁模型的第3阶振型

(h) 多尺度模型的第3阶振型

(i) 细观实体模型的第3阶振型

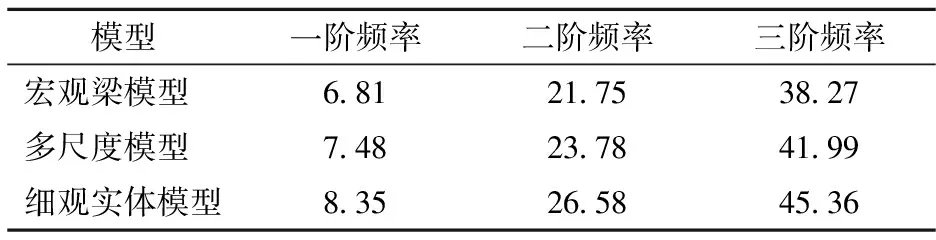
表1 不同模型下结构的自振频率 Hz

3.4 多尺度模型拟静力响应验证

图13为多尺度模型的整体变形图．由图可知,在梁柱较大弯矩作用下,底层节点呈现出明显的损伤状态,中柱拉梁层的应力值最大,混凝土破损严重,这与图10的试验结果一致．图14为多尺度模型计算结果与试验结果的荷载-位移关系曲线对比．由图可知,在框架加载后期,随着荷载循环次数的增多和位移的增大,钢筋混凝土框架承载力及刚度不断降低．模型的计算结果与试验结果虽存在一定偏差,但变化趋势一致．因此,采用多尺度模型进行建模,不仅能实现整体结构受力行为的模拟,还能反映出关键部位的受力变化,是准确研究结构损伤的有效途径之一．

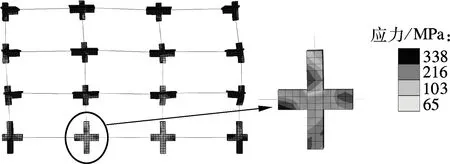
图13 多尺度模型变形云图

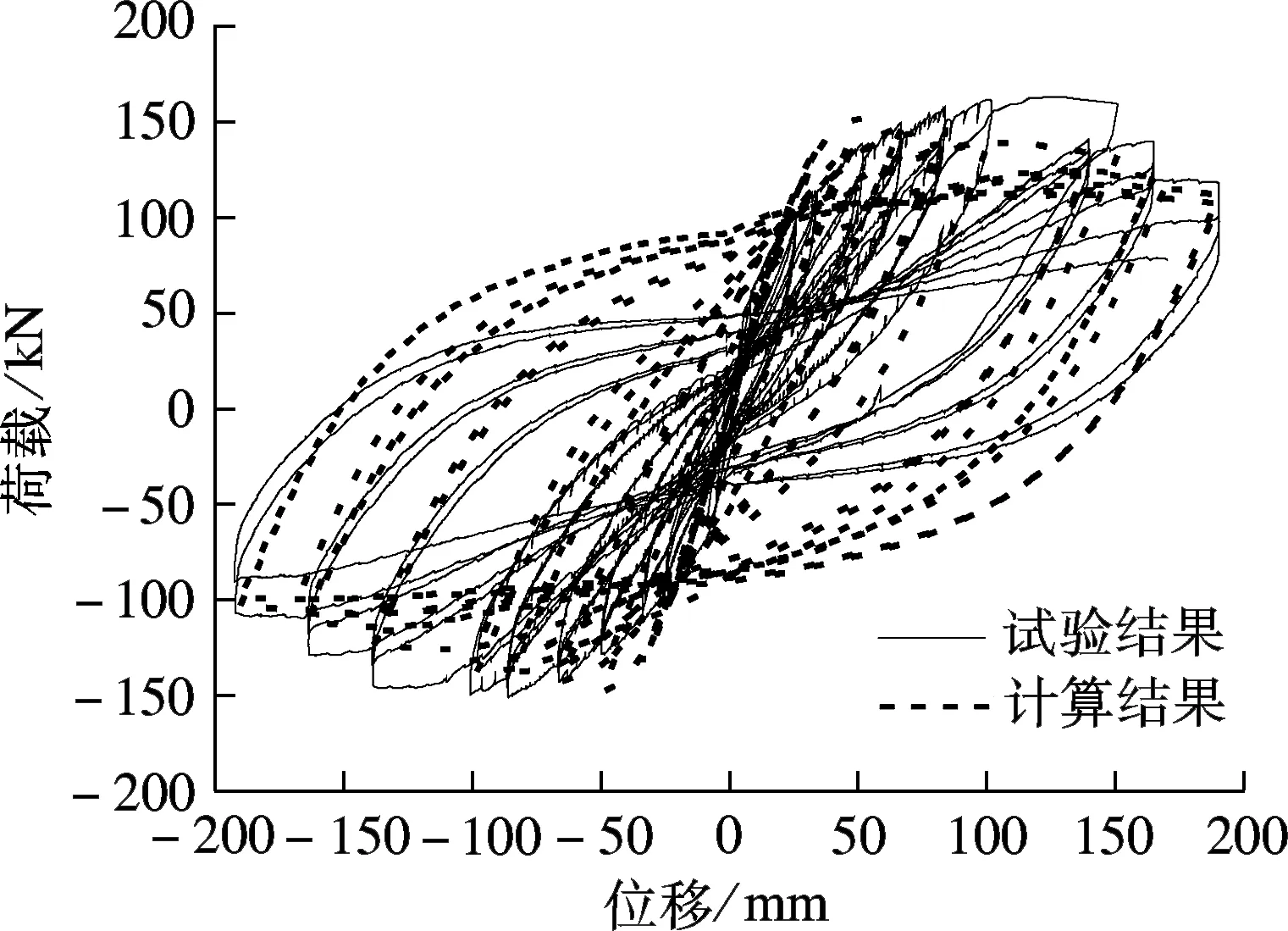
图14 荷载-位移关系曲线对比

表2列出了3种有限元模型的单元数和计算时间比较．由表可知,细观实体模型单元数多,计算量大,耗时长;而宏观梁模型的单元数少,计算量小,耗时短．虽然梁模型的计算效率高,但它无法反映关键构件的局部变化过程．多尺度模型则介于两者之间,兼顾了整体结构模型的计算效率和关键部位的计算精度,适用于大型复杂土木工程结构的计算．

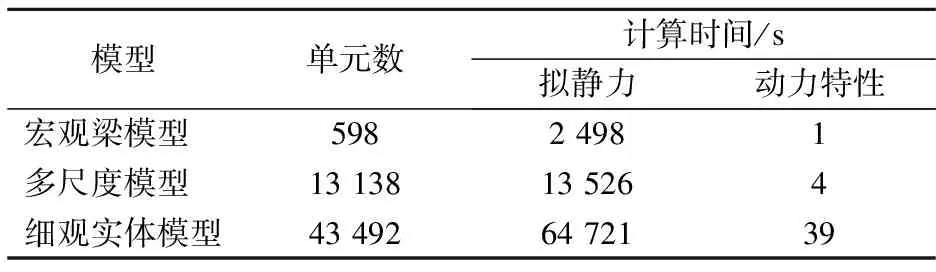
表2 有限元模型的单元数和计算时间对比

4 结论

1) 根据变形协调方法处理多尺度模型界面连接时,在轴力作用下,实体单元的界面节点由于受到泊松效应的影响,会在截面内发生约束,出现应力不均匀现象,这与实际受力状态不符．

2) 运用力的平衡方法处理多尺度模型界面连接,能够有效实现不同尺度单元之间的过渡,从而可以将精细模型植入整个宏观梁单元模型结构中,进行多尺度结构计算．

3) 在静力荷载作用下,运用力的平衡方法处理界面连接较运用变形协调方法更符合实际受力情况．在动力荷载作用下,2种界面连接方法都是可行的．

4) 采用多尺度模型进行建模,不仅能实现结构整体受力行为的模拟,还能反映出关键部位的受力变化,计算效率明显提高．

References)

[1]林旭川, 陆新征, 叶列平. 钢-混凝土混合框架结构多尺度分析及其建模方法[J]. 计算力学学报, 2010, 27(3): 469-475. Lin Xuchuan, Lu Xinzheng, Ye Lieping. Multi-scale finite element modeling and its application in the analysis of a steel concrete hybrid frame [J].ChineseJournalofComputationalMechanics, 2010, 27(3): 469-475. (in Chinese)

[2]Yu Q, Fish J. Multiscale asymptotic homogenization for multiphysics problems with multiple spatial and temporal scales: a coupled thermo-viscoelastic example problem [J].InternationalJournalofSolidsandStructures, 2002, 39(26): 6429-6452.

[3]Oskay C, Fish J. Multiscale modeling of fatigue for ductile materials [J].InternationalJournalforMulti-scaleComputationalEngineering, 2004, 2(3): 329-353.

[4]Hund A, Ramm E. Application of the variational multiscale method to damage of composites [C]//Proceedingofthe11thInternationalConferenceonFracture. Turin, Italy, 2005:1092-1097.

[5]陈志文, 李兆霞, 卫志勇. 土木结构损伤多尺度并发计算方法及其应用[J]. 工程力学, 2012, 29(10): 205-210. Chen Zhiwen, Li Zhaoxia, Wei Zhiyong. Concurrent multi-scale computational method for damage analyses of civil structures [J].EngineeringMechanics, 2012, 29(10): 205-210. (in Chinese)

[6]Li Z X, Chan T H T, Yu Y, et al. Concurrent multi-scale modeling of civil infrastructures for analyses on structural deterioration—part Ⅰ: modeling methodology and strategy [J].FiniteElementsinAnalysisandDesign, 2009, 45(11): 782-794.

[7]Li Z X, Zhou T Q, Chan T H T, et al. Multi-scale numerical analysis on dynamic response and local damage in long-span bridges [J].EngineeringStructures, 2007, 29(7): 1507-1524.

[8]李兆霞. 大型土木结构多尺度损伤预后的现状、研究思路与前景[J]. 东南大学学报:自然科学版, 2013, 43(5): 1111-1121. Li Zhaoxia. State of the art in multi-scale damage prognosis for major infrastructures [J].JournalofSoutheastUniversity:NaturalScienceEdition, 2013, 43(5): 1111-1121. (in Chinese)

[9]石永久, 王萌, 王元清. 基于多尺度模型的钢框架抗震性能分析[J]. 工程力学, 2011, 28(12): 20-26. Shi Yongjiu, Wang Meng, Wang Yuanqing. Seismic behavior analysis of steel frame by multi-scale calculation method [J].EngineeringMechanics, 2011, 28(12): 20-26. (in Chinese)

[10]Michopoulos G, Farhat C, Fish J. Modeling and simulation of multiphysics systems [J].JournalofComputingandInformationScienceinEngineering, 2005, 5(3): 198-213.

[11]Ladevèze P, Nouy A, Loiseau O. A multi-scale computational approach for contact problems [J].ComputerMethodsinAppliedMechanicsandEngineering, 2002, 191(43): 4869-4891.

[12]陆新征. 钢筋混凝土框架结构拟静力倒塌实验[EB/OL]. (2011-06-20)[2014-01-12]. http://www.collapse-prevention.net/download/Frame_Collapse_Newletter_01.pdf.

[13]陆新征, 叶列平, 潘鹏, 等. 钢筋混凝土框架结构拟静力倒塌试验研究及数值模拟竞赛Ⅰ: 框架试验[J]. 建筑结构, 2012, 42(11): 19-22. Lu Xinzheng, Ye Lieping, Pan Peng, et al. Pseudo-static collapse experiments and numerical prediction competition of RC frame structure Ⅰ: RC frame experiment [J].BuildingStructure, 2012, 42(11): 19-22. (in Chinese)

[14]Lubliner J, Oliver J, Oller S, et al. A plastic-damage model for concrete [J].InternationalJournalofSolidsandStructures, 1989, 25(3): 299-326.

Interface connection method of multi-scale modeling of concrete structure

Zhang Ying Sun Guangjun Li Hongjing

(College of Civil Engineering, Nanjing Technology University, Nanjing 210009, China)

The deformation coordination method and the force balance method are individually used to establish multi-scale models of a single column. The stress distribution under the static force and the deformation behavior under the dynamic force of the column are analyzed, and the reasonability of the connection between different interfaces in multi-scale models is verified. On this basis, a three-storey reinforced concrete frame is taken as an example, and a solid element model, a beam element model and a multi-scale model under interfacial connection of force balance are established. The cyclic loading performance of the multi-scale model is calculated and compared with the experimental results to verify the effectiveness of the interface connection method of force balance. The results show that under static loads, the model under interface connection of force balance conforms to actual situation better than that under deformation coordination. However, under dynamic loads, both interface connection modes are feasible. Therefore, simulating the whole structure by using the multi-scale model can accurately implement the simulation of the overall structure behavior, reflect the stress behaviors of the key parts and improve the calculation efficiency obviously.

concrete structure; multi-scale model; deformation coordination; force balance; interface connection

2014-07-29. 作者简介: 张莹(1988—)，女，博士生；孙广俊(联系人)，男，博士，副教授，gjsun2004@163.com.

江苏省自然科学基金资助项目(BK20130937)、江苏省普通高校研究生科研创新计划项目(CXZZ13_0441)、东南大学混凝土及预应力混凝土结构教育部重点实验室开放课题基金资助项目(CPCSME2011-04).

张莹,孙广俊,李鸿晶.混凝土结构多尺度建模界面连接方法[J].东南大学学报:自然科学版,2015,45(1):126-132.

10.3969/j.issn.1001-0505.2015.01.023

TU375

A

1001-0505(2015)01-0126-07