短轴向剪切加载模式下超大型黏弹阻尼墙力学性能试验

许俊红 李爱群

(东南大学土木工程学院, 南京 210096)

短轴向剪切加载模式下超大型黏弹阻尼墙力学性能试验

许俊红 李爱群

(东南大学土木工程学院, 南京 210096)

为了提高黏弹性阻尼装置温度相关性的准确度、最大阻尼力和力学性能,首先开展了黏弹性材料的温度扫描试验,然后设计了一种新式阻尼装置试验方法,即短轴向剪切加载模式方法,采用该试验方法对新型“5+4”式超大型黏弹性阻尼墙构件进行了力学性能试验.试验给出了黏弹性材料的tanδ-T,G′-T,G″-T曲线、黏弹性阻尼墙构件力-位移滞回曲线以及力学性能参数(最大阻尼力、损耗因子、等效阻尼系数、存储刚度、损耗刚度、剪切损耗模量、剪切储能模量等)的频率相关性和位移幅值相关性等.结果表明:黏弹性阻尼墙损耗因子峰值(0.77)与由黏弹性材料温度扫描试验得出的损耗因子峰值(0.79)只有微小差别,说明所设计的“5+4”黏弹性阻尼墙构件在短轴向剪切加载模式下可以很好发挥黏弹性阻尼材料的阻尼性能.

温度扫描;短轴向剪切加载;“5+4”黏弹性阻尼墙;最大阻尼力;损耗因子

1969年,为减小纽约世界贸易中心大楼(110层)在风振作用下的侧位移,在支撑楼板的桁架梁的下翼缘处,从第10层至110层共计10 000个黏弹性阻尼器被安装在双子塔两侧[1].1994年,经由美国科罗拉多州立大学1/120缩尺模型风洞试验后[2],中国台北捷运系统Chien-Tan火车站悬吊屋顶采用8个黏弹性阻尼器以降低风振影响.随后黏弹性阻尼器应用于以减小地震反应为目标的工程领域,美国圣克拉拉市的一栋13层钢框架结构开始采用黏弹性阻尼器控制地震响应[3].黏弹性阻尼器不仅在新建结构中,而且对已有结构的抗震(振)加固也能有很好的功能.在土木工程领域，黏弹性阻尼装置被公认为是抗风抗振方面最为有效的振动控制装置之一[4].

近年来,有关研究表明,黏弹性阻尼装置能提供给建筑结构相应的阻尼比,从而有效降低结构的层间剪力、层间位移和楼层加速度[5-9].因此涌现了大量的关于黏弹性阻尼装置的研究成果和实践工程,产生了不同构造形式的黏弹性阻尼装置,但目前在黏弹性阻尼装置的研究中尚存在以下问题:① 对黏弹性阻尼装置所用的耗能材料尚缺乏相关的试验研究分析,对黏弹性材料的温度相关性缺少试验支撑数据.通常情况下,黏弹性阻尼装置的温度相关性采取设置保温箱的形式.② 常用的方柱形黏弹性阻尼器以支撑的形式应用于建筑层间,其应用范围受到了较大的限制,而黏弹性阻尼墙可较好地适应建筑的需要,但国内外有关黏弹性阻尼墙的研究尤其是试验研究开展得很少,这在很大程度上限制了其实际工程应用.③ 黏弹性阻尼装置的试验加载模式普遍采用平行于长轴向施加循环荷载,为了更符合构件在实际受荷状况下的模型,本文设计了一种新式加载方法,即短轴向剪切加载.④ 传统的黏弹性阻尼构件力学性能分析一般集中在模量和损耗因子两方面,而对于黏弹性阻尼装置的其他力学性能如存储刚度、损耗刚度和等效阻尼系数等尚缺乏应有的研究.

为此,本文针对黏弹性阻尼墙开展了黏弹性阻尼装置所用阻尼材料的动态力学试验;设计了一种“5+4”式(即5层钢板夹4层黏弹性材料)的超大型阻尼墙足尺模型,并对其开展了一系列相关试验研究.

1 黏弹阻尼材料温度扫描试验

为了提高黏弹性阻尼装置温度相关性的准确度,本文首先对构件所用的黏弹性阻尼材料进行了温度扫描试验.试验仪器采用日本UBM公司的Rheogel-E4000DMA测试仪,得到了该材料在0.5,1.5,2.5 Hz三种频率、0～40 ℃温域内的基本力学性能曲线,即G′-T,G″-T和tanδ-T曲线,如图1所示.图中，G′，G″分别为剪切储存模量和剪切损耗模量.由图可知,该阻尼材料性能稳定,在3种频率工况下,都于常温20 ℃左右到达玻璃态转变区.而且从曲线上可明确看出材料阻尼性能随温度的变化趋势,损耗因子的峰值为0.79.因此,本次黏弹性阻尼结构力学性能试验可只考虑位移幅值和频率2种因素.

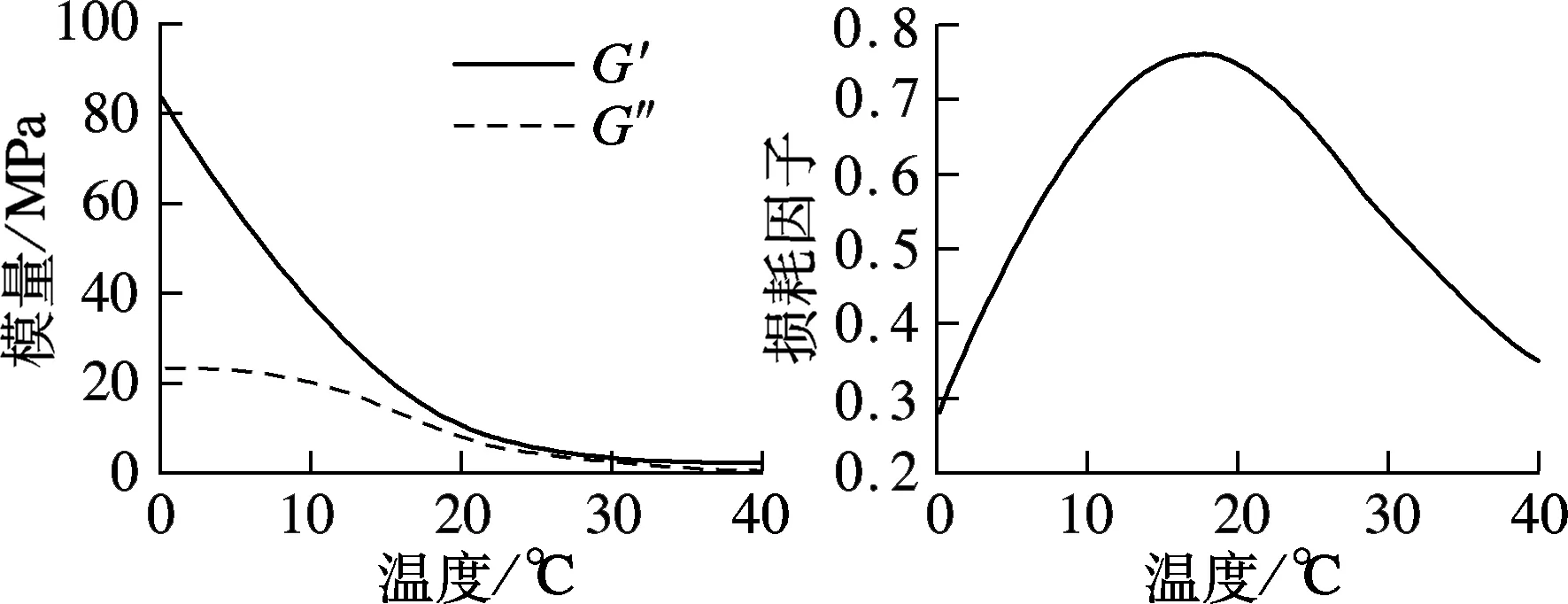
(a) 0.5 Hz时黏弹性阻尼材料的模量值和损耗因子

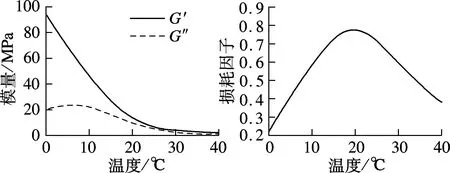
(b) 1.5 Hz时黏弹性阻尼材料的模量值和损耗因子

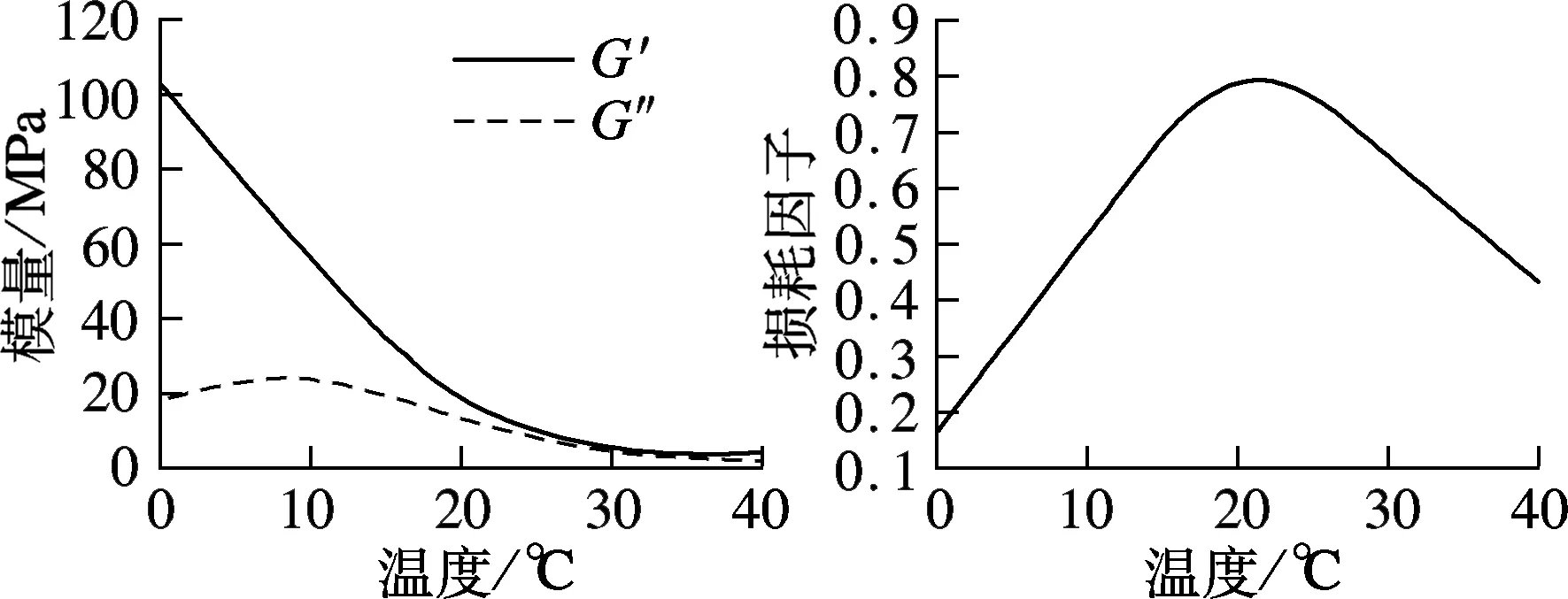
(c) 2.5 Hz时黏弹性阻尼材料的模量值和损耗因子

2 黏弹性阻尼墙试验

2.1 黏弹性阻尼墙构件规格

本次试验的“5+4”新型黏弹性阻尼墙(VDW)是由东南大学抗震设计研究中心和常州兰锦橡塑有限公司合作开发研制,为足尺构件,其构造及尺寸如图2(a)所示,其中4层黏弹性材料层每层厚度为10 mm,中间钢板为20 mm,两侧4块约束钢板为12 mm.VDW截面有效尺寸为500 mm×500 mm,黏弹性材料层覆占面积为10 000 mm2,中间钢板及外侧钢板上下各延出200 mm,总尺寸为900 mm×500 mm.

2.2 短轴向剪切加载装置设计

由上述构件尺寸及规格设计的加载装置,3D示意图如图2(b)所示.整个系统由底部固定支架和上端施载夹具构成,中间部分为黏弹性阻尼墙构件.已安装到位的试验装置立面、平面图如图2(c)和(d)所示.

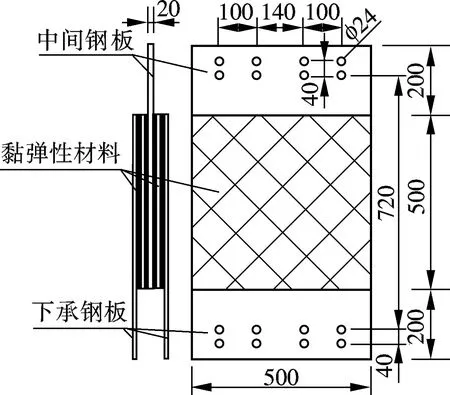
(a) VDW尺寸图(单位：mm)

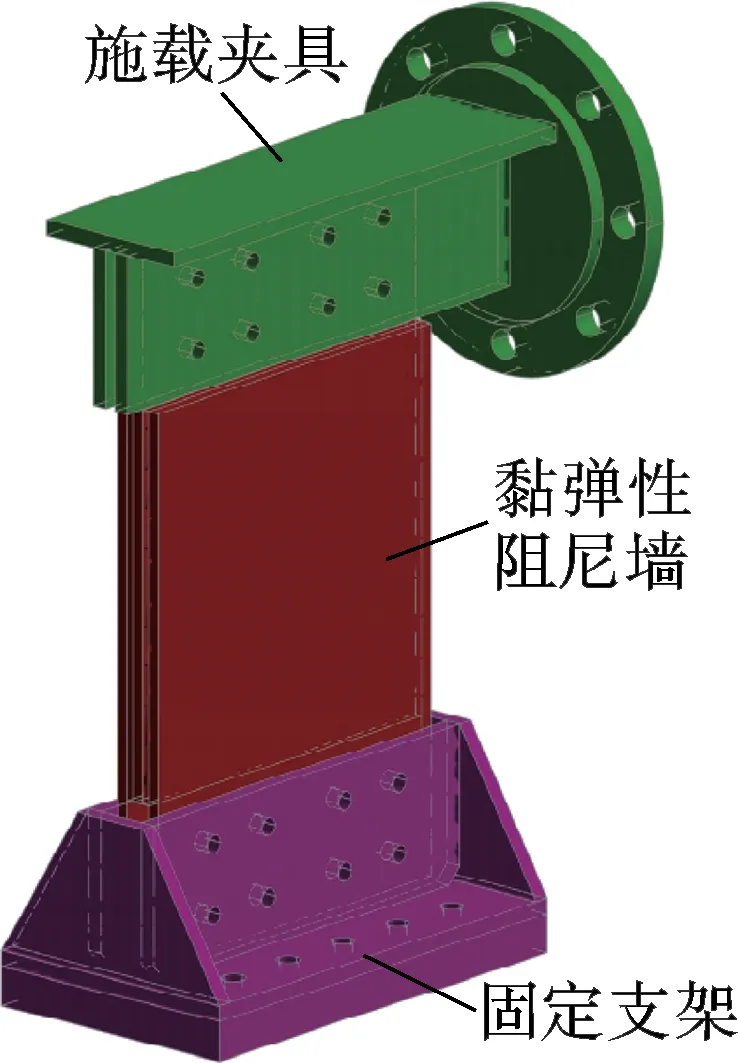
(b) 加载装置3D图

(c) 试验装置立面

(d) 试验装置平面

2.3 试验工况及构件阻尼性能评价方法

按照《建筑消能阻尼器》[10]行业标准中规定,加载5个循环,并取第3个滞回圈作为试验标准曲线.试验在室温条件下进行,并考虑频率相关性和位移幅值相关性,试验工况选用了0.5,1.0,1.5,2.0 Hz四种频率和22.5,30.0,37.5,45.0,60.0 mm五种位移幅值.

2.4 力-位移滞回曲线

试验在室温(现场测量温度为21.2 ℃)条件下进行.图3为黏弹性阻尼墙分别在频率为0.5,1.0,1.5,2.0 Hz和位移幅值为22.5,30.0,37.5,45.0, 60.0 mm时的力-位移(F-u)滞回曲线.由图可知,滞回环并非光滑的椭圆,而是出现了棱角,说明组成该阻尼墙的黏弹性材料分子之间及分子-填充料之间的摩擦阻尼单元以黏滞性为主体.

3 力学性能指标分析

由试验得出的滞回曲线组计算得出黏弹性阻尼墙的一系列力学性能指标.

3.1 最大阻尼力

最大阻尼力Fmax为当黏弹性阻尼墙构件达到某一位移幅值时构件所能承受的最大荷载.由图4(a)可知,当频率为0.5 Hz、位移幅值为60.0 mm时,构件出现的最大阻尼力为241.5 kN.四种频率下最大阻尼力的增长斜率基本保持一致,当频率低于1.0 Hz时,最大阻尼力呈单调增长模式；当频率为1.5和2.0 Hz时,最大阻尼力在位移幅值达到45.0 mm前单调递增，大于45.0 mm后，则单调递减，呈抛物线型变化.对于最大阻尼力与频率相关性来说,除位移幅值为60.0 mm外,整个频率段的最大阻尼力保持不变.

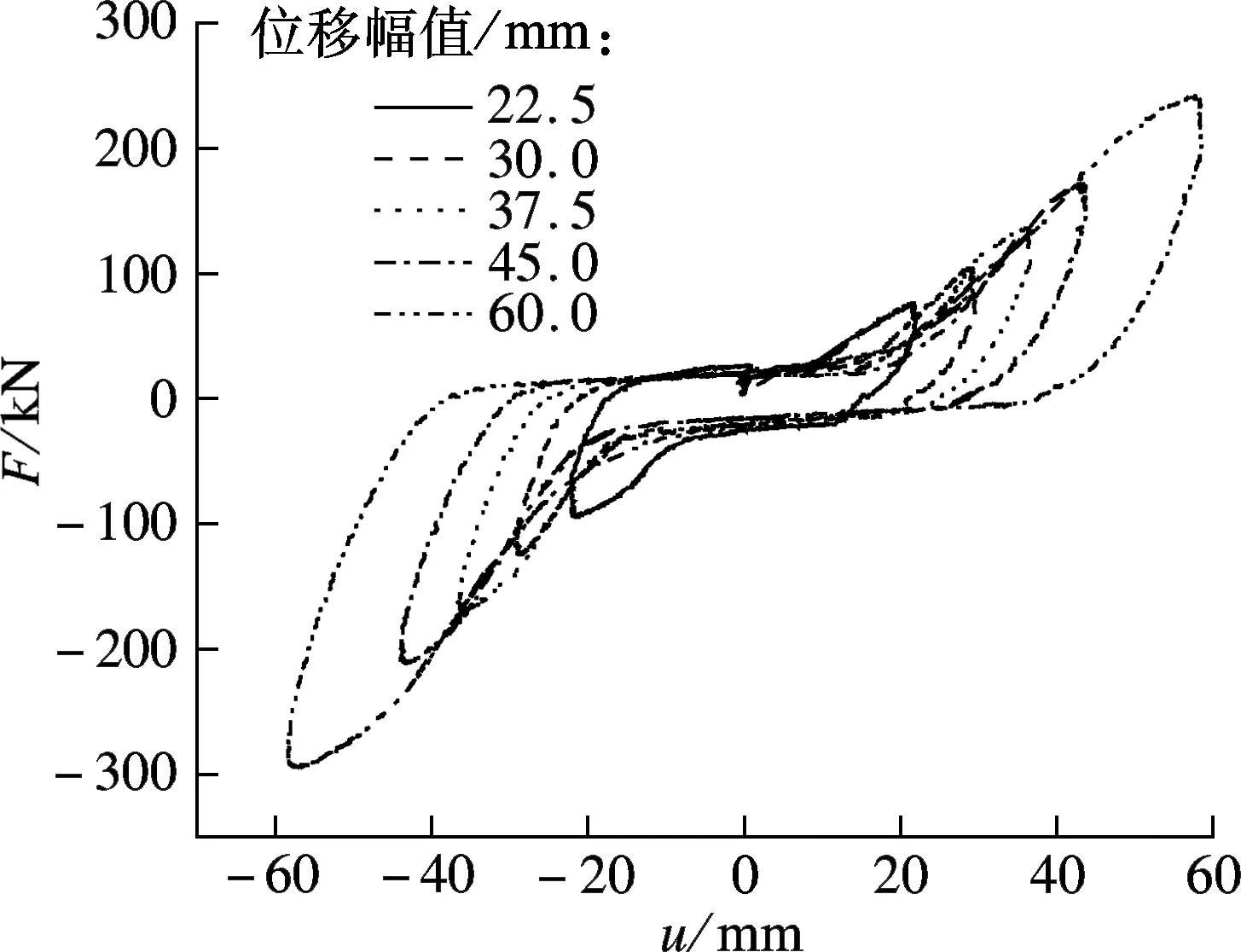
(a) 0.5 Hz

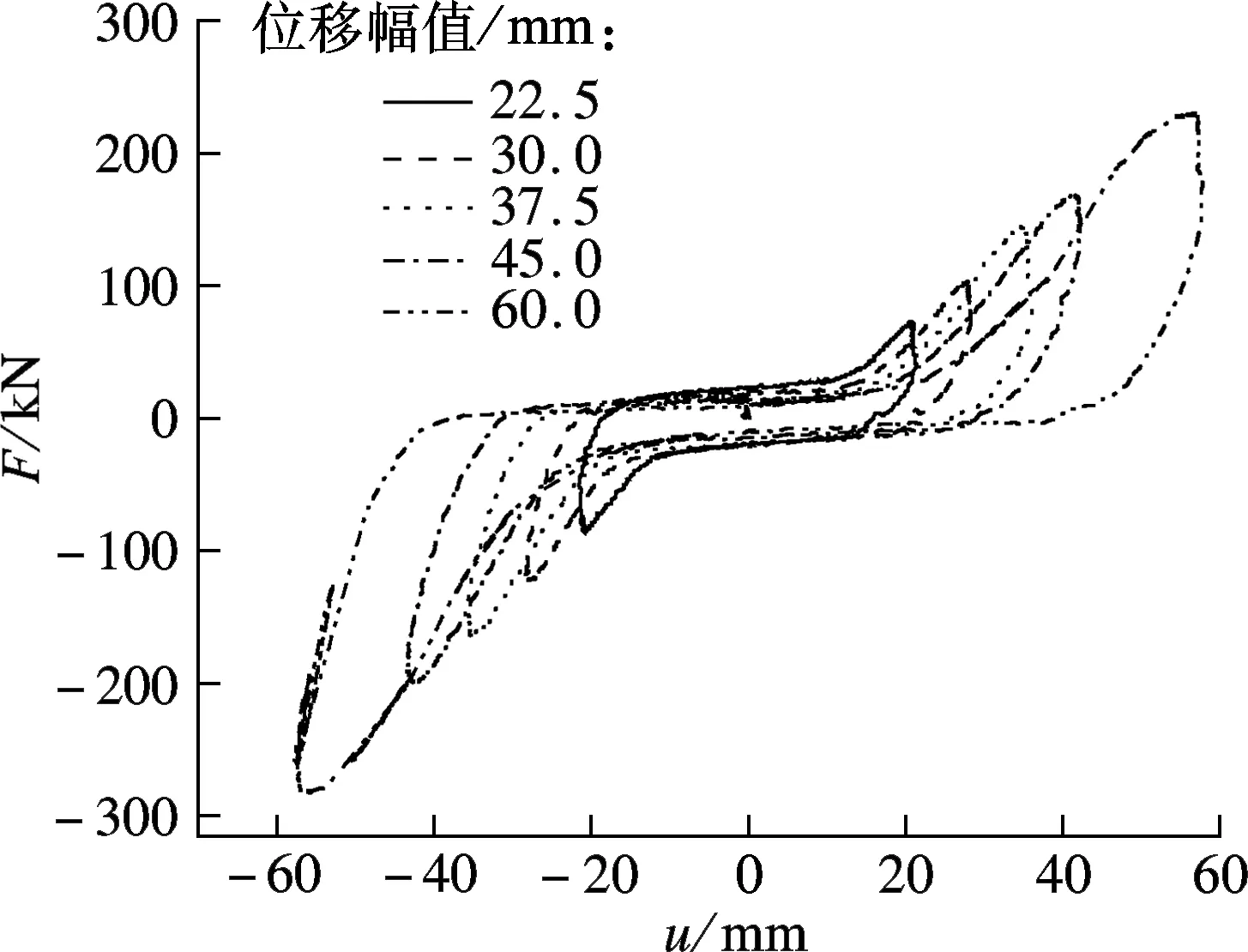
(b) 1.0 Hz

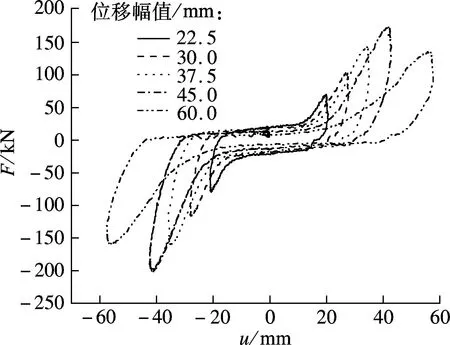
(c) 1.5 Hz

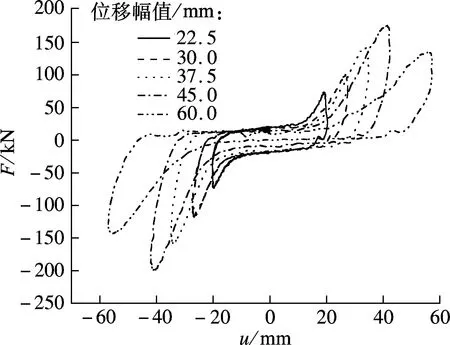
(d) 2.0 Hz

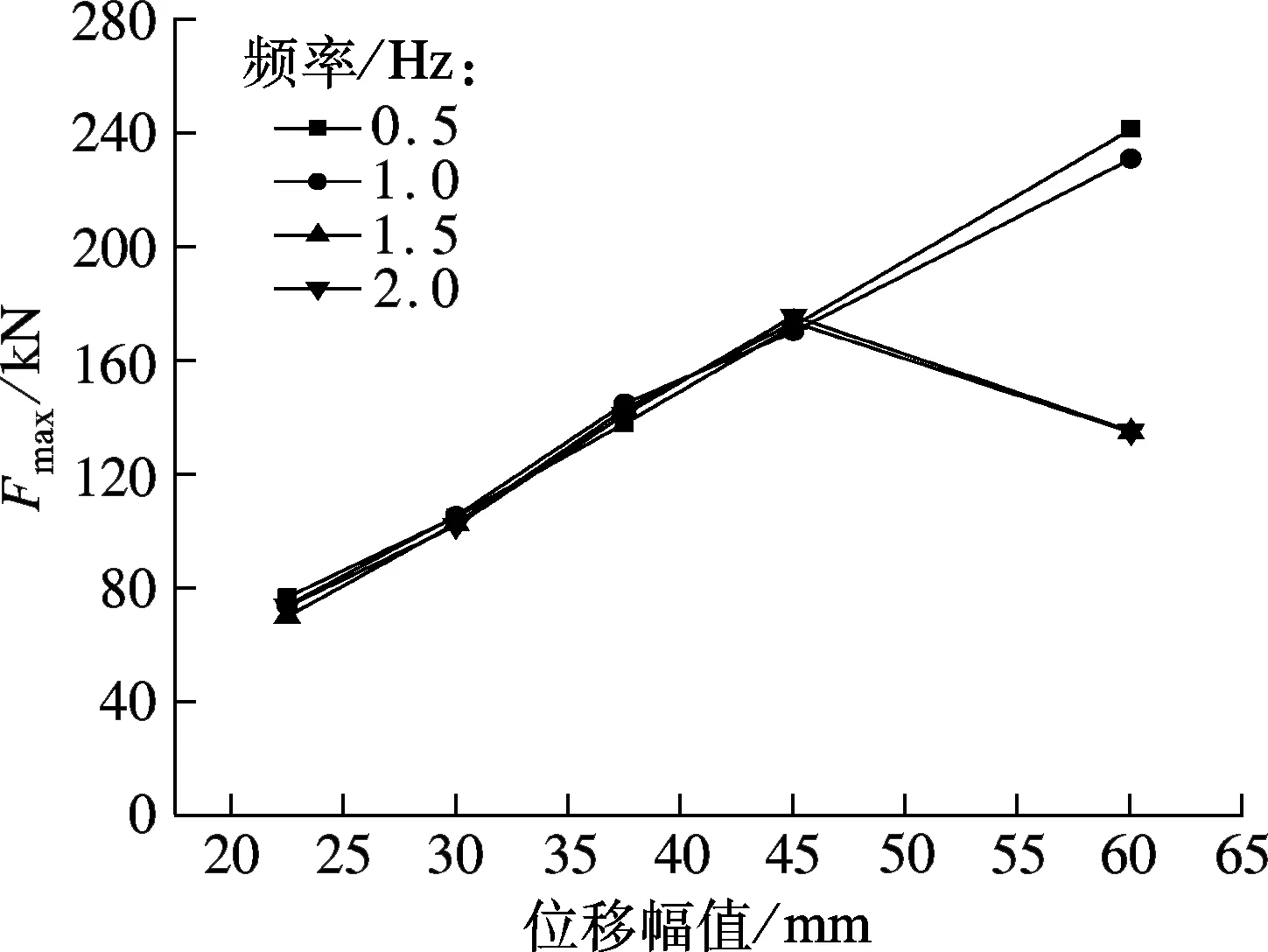
(a) 最大阻尼力的位移相关性分析图

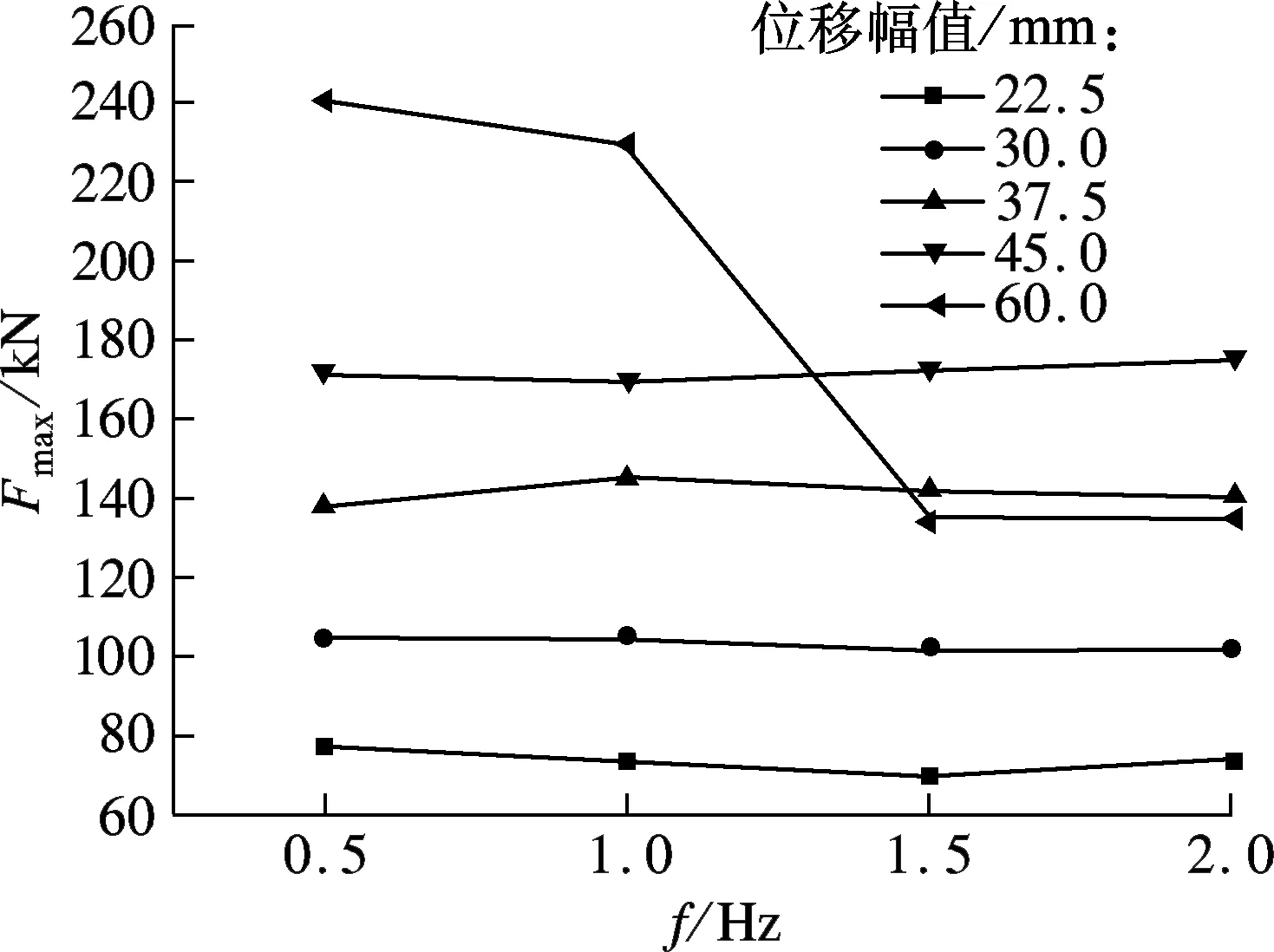
(b) 最大阻尼力的频率相关性分析图

3.2 存储刚度

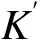
3.3 损耗刚度

损耗刚度K″d定义为构件的最大黏滞力(零位移时的荷载)与最大位移的比值.它反应了黏弹性阻尼墙构件在能量损耗方面的能力.从图6(a)可知,在每种频率下,构件损耗刚度皆随位移幅值的增大呈单调递减变化,递减率几乎保持一致.而对于损耗刚度的频率相关性分析来看,除最大位移幅值60.0 mm外,其他位移幅值与频率几乎零相关.

3.4 等效阻尼系数

(a) 存储刚度的位移相关性分析图

(b) 存储刚度的频率相关性分析图

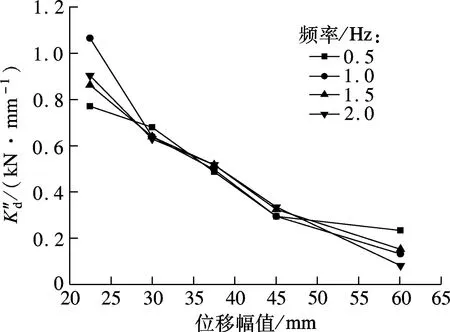
(a) 损耗刚度的位移相关性分析图

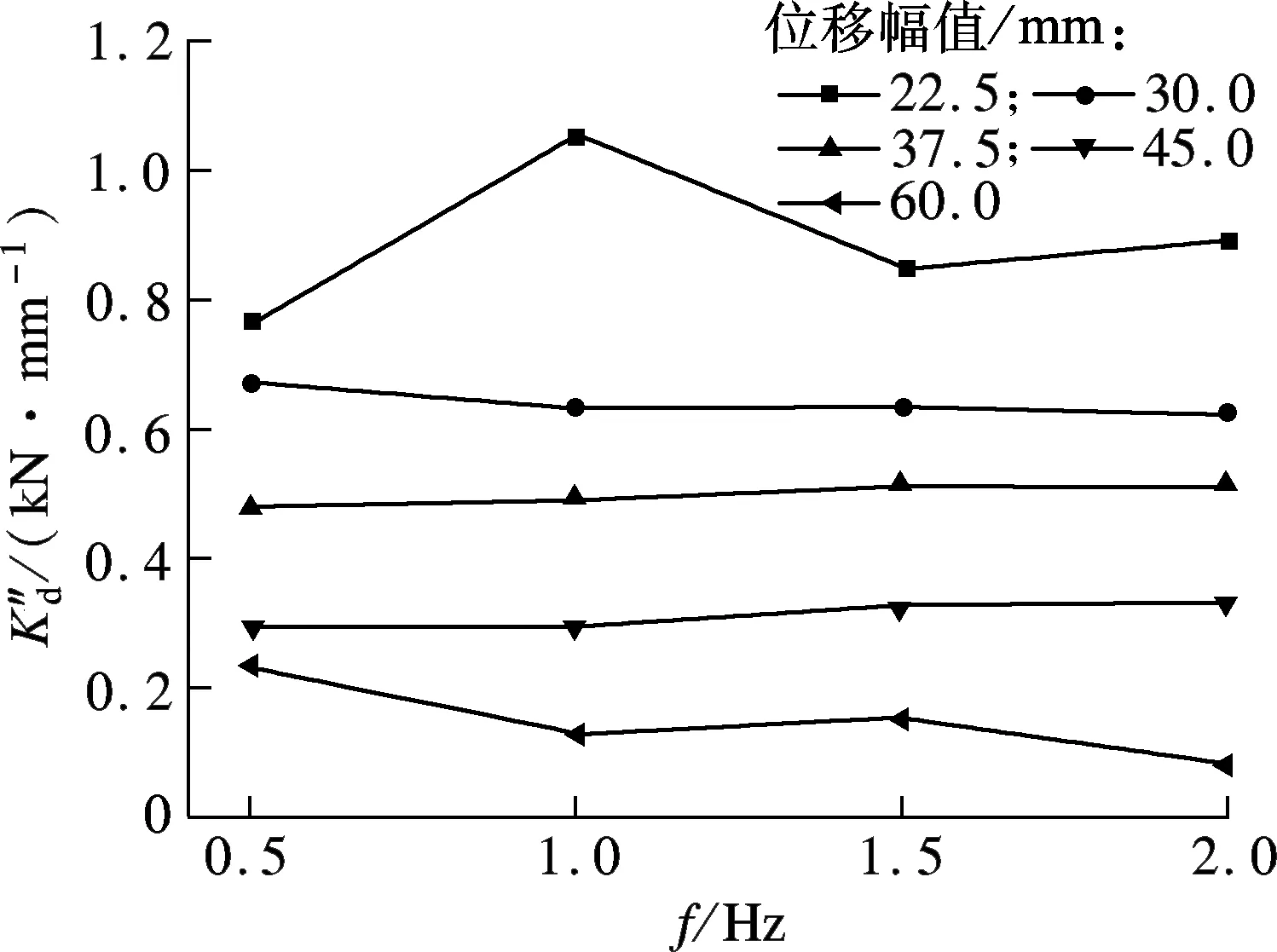
(b) 损耗刚度的频率相关性分析图

等效阻尼系数Cd即等效黏滞系数,定义为损耗刚度与加载频率的比值.由此定义可知,等效阻尼系数在某种程度上与损耗刚度保持一定的关联,如图7(a)所示,在位移相关性上,在每种频率下,构件等效阻尼系数皆随位移幅值的增大呈单调递减变化,当频率为0.5 Hz时等效阻尼系数远大于其他频率的等效阻尼系数.但等效阻尼系数在频率相关性上则与损耗刚度不同,在每种位移幅值工况下,等效阻尼系数随着频率的减小也在逐渐减小,其中在频率为0.5 Hz、位移幅值为22.5 mm时等效阻尼系数达到最大(1.52 kN·s/mm).

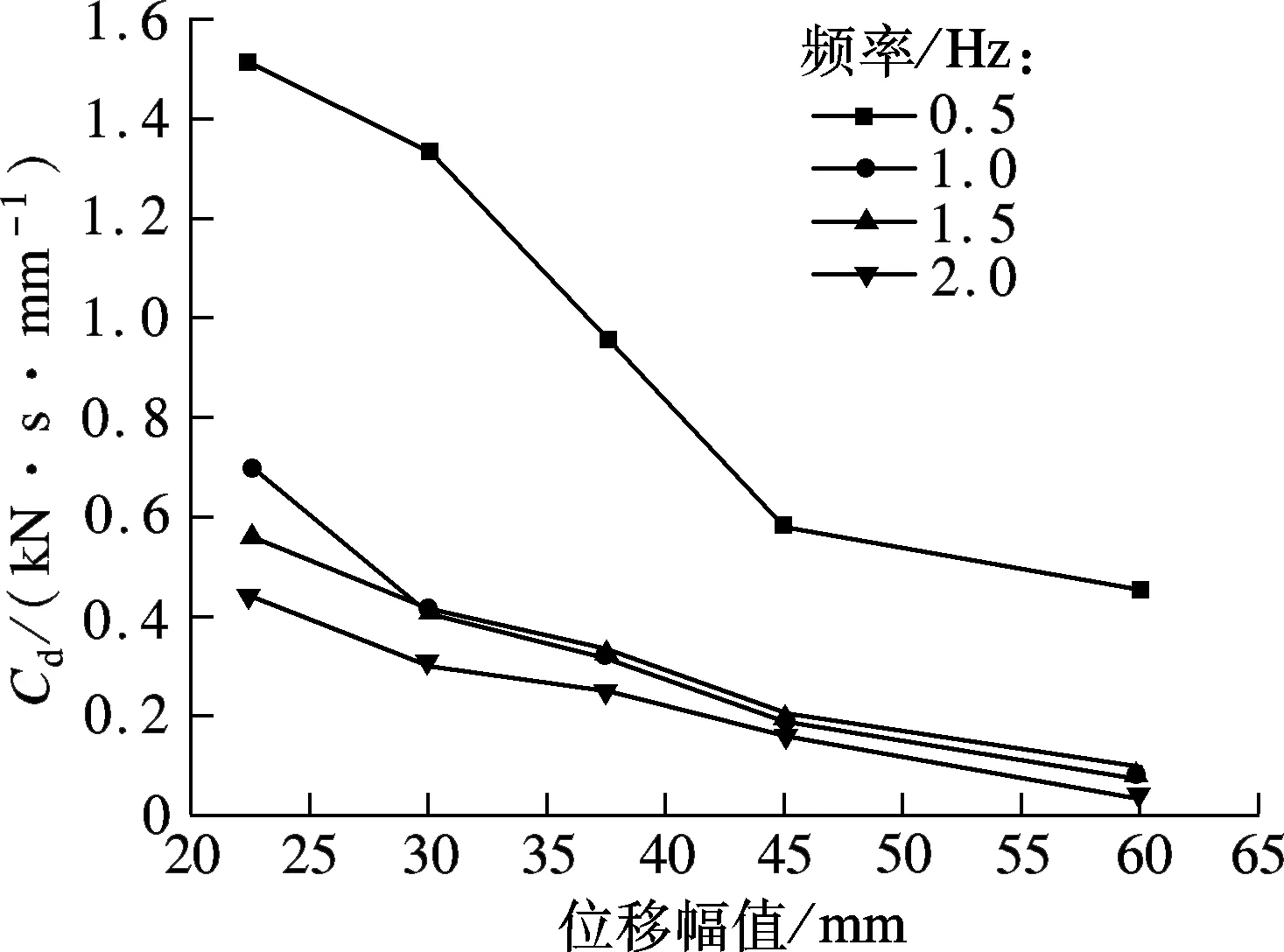
(a) 等效阻尼系数的位移相关性分析图

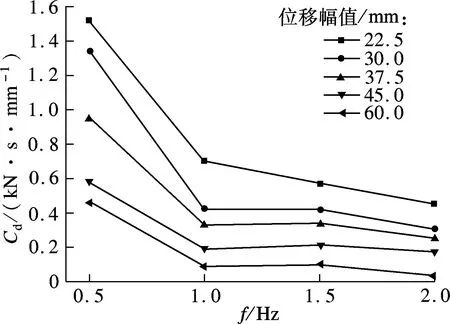
(b) 等效阻尼系数的频率相关性分析图

3.5 剪切储存模量

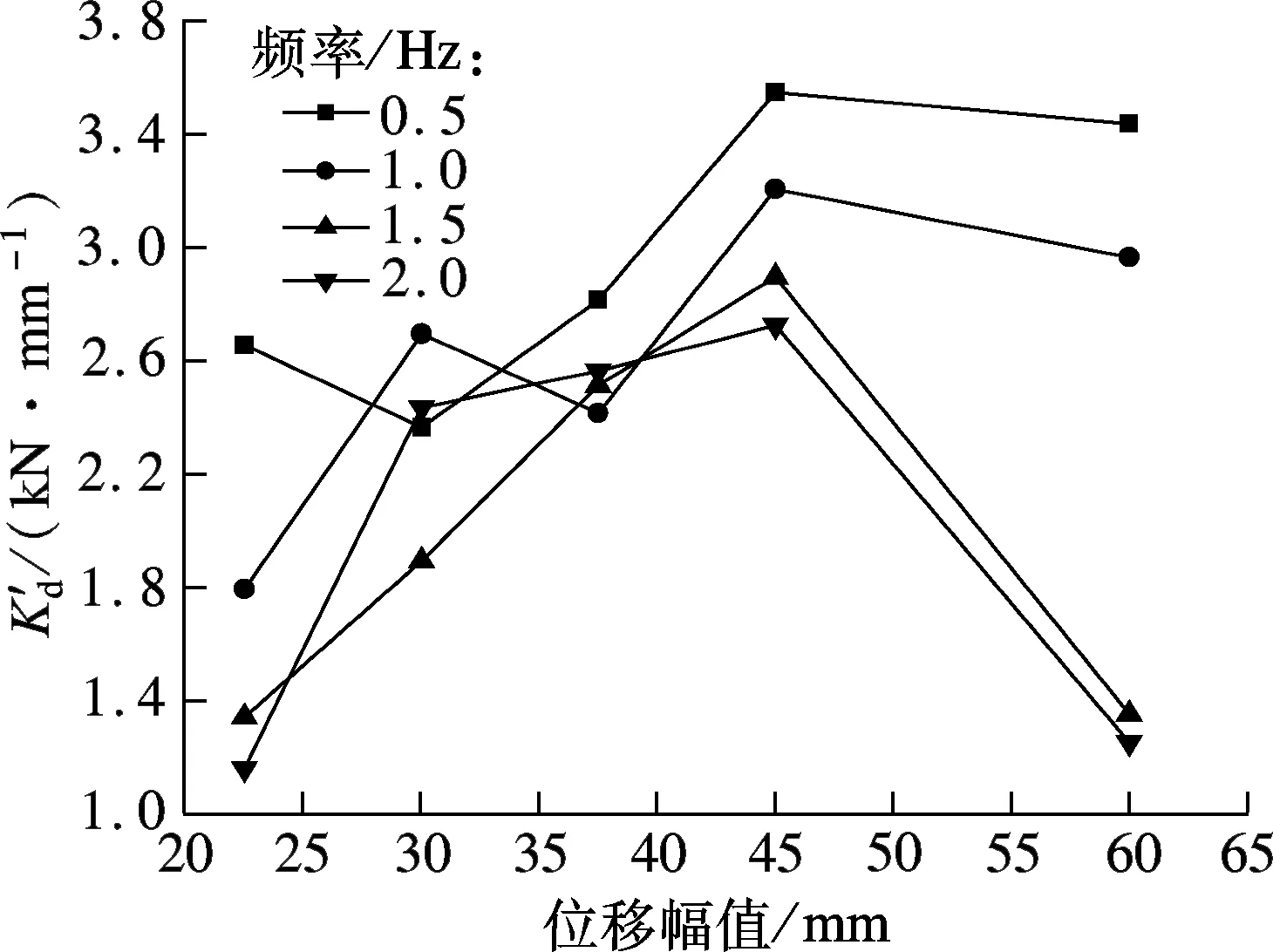
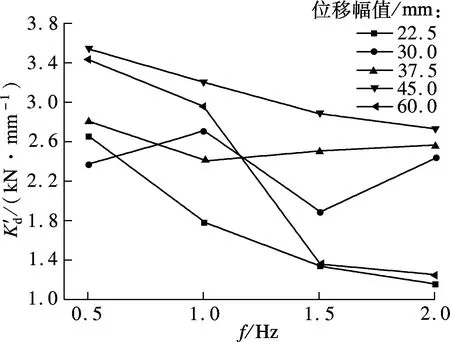
剪切储存模量G′定义为存储刚度和黏弹性材料层厚度的乘积再与黏弹性材料受剪面积的比值.从该定义可知,剪切储存模量的位移相关性和频率相关性与存储刚度保持高度一致.由图8(a)可知,每种频率工况下构件的剪切储存模量随位移幅值呈抛物线型变化,4种频率下皆当位移幅值为45.0 mm时剪切储存模量达到最大,最大值随着频率的增大而减小,当频率最小(0.5 Hz)时剪切储存模量达到最大(3.54 MPa),当频率最大(2.0 Hz)时剪切储存模量达到最小(2.7 MPa).由图8(b)的整个趋势来看,除位移幅值为30.0和37.5 mm两种情况出现偏差外,其他位移幅值工况下构件的剪切储存模量则随频率呈单调递减变化.

3.6 剪切损耗模量

剪切损耗模量G″定义为损耗刚度和黏弹性材料层厚度的乘积再与黏弹性材料受剪面积的比值.从该定义可知,剪切储存模量的位移相关性和频率相关性与损耗刚度保持高度一致.由图9(a)可知,在每种频率下,构件剪切损耗模量皆随位移幅值的增大呈单调递减变化,递减率几乎保持一致.而从剪切损耗模量的频率相关性分析来看,除最大位移幅值60.0 mm外,其他位移幅值与频率几乎零相关.

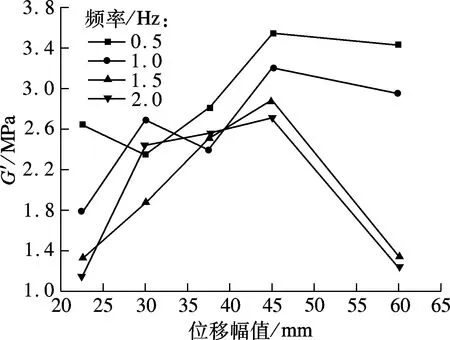
(a) 剪切储存模量的位移相关性分析图

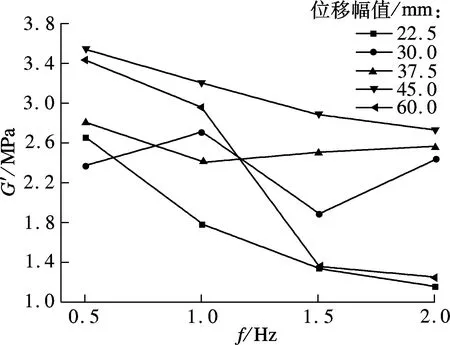
(b) 剪切储存模量的频率相关性分析图

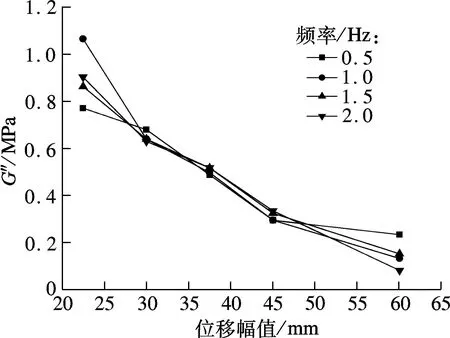
(a) 剪切损耗模量的位移相关性分析图

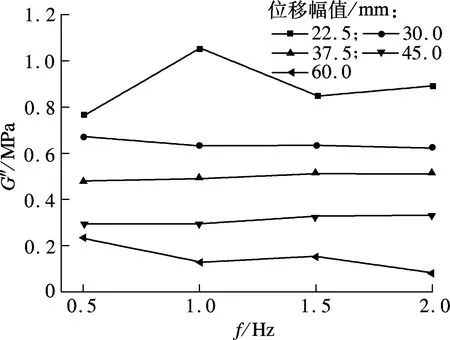
(b) 剪切损耗模量的频率相关性分析图

3.7 损耗因子

损耗因子η即损失系数,定义为损失刚度与存储刚度之比,即最大黏滞力(零位移时的荷载)与最大弹性力(最大位移时的荷载)的比值.由图10(a)可知,损耗因子在4种频率工况下,其值皆随着位移幅值的增大而减小,当频率为2.0 Hz、位移幅值为22.5 mm情况下，损耗因子出现峰值(0.77),处于一个比较高的状态.

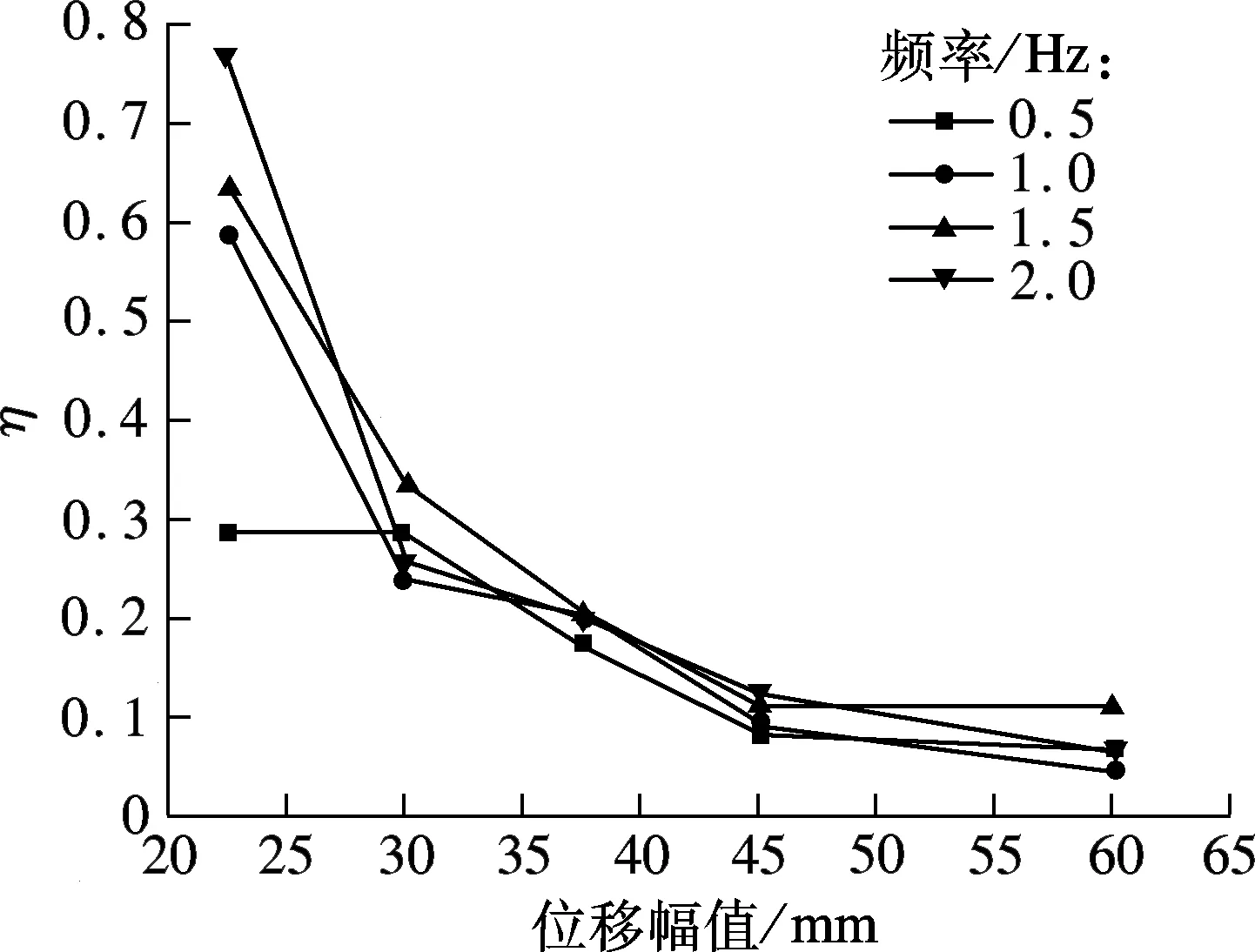
(a) 损耗因子的位移相关性分析图

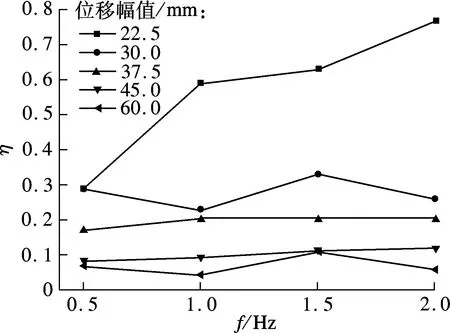
(b) 损耗因子的频率相关性分析图

4 结论

1) 通过直接对黏弹性阻尼材料进行温度扫描试验,可间接得出黏弹性阻尼墙构件随温度的变化规律,更精确和直观.

2) 等效阻尼系数与频率呈递减关系,最大阻尼力、损耗刚度、损耗因子和剪切损耗模量与频率则呈现零相关,存储刚度、剪切储存模量则在位移幅值为30.0和37.5 mm时,随着频率的升高先减后增.

3) 存储刚度和剪切储存模量与位移幅值呈抛物线型变化,当位移幅值达到45.0 mm、频率为0.5 Hz时存储刚度和剪切储存模量达到峰值,分别为3.54 kN/mm和2.7 MPa;损耗刚度、损耗因子和剪切损耗模量则与位移呈单调递减变化;当频率为0.5和1.0 Hz时,最大阻尼力呈单调增加;当频率升高至1.5和2.0 Hz时最大阻尼先增后减,最大阻尼力皆在位移幅值达到45.0 mm时达到峰值,分别为173.5 kN和175.7 kN.

4) 当频率为2.0 Hz、位移幅值为22.5 mm情况下,损耗因子出现峰值0.77,这与黏弹性材料温度扫描试验得出的损耗因子的峰值0.79只有微小差别,说明本文设计的“5+4”式黏弹性阻尼墙在短轴向剪切加载模式下可以很好地发挥黏弹性阻尼材料的阻尼性能,为黏弹性阻尼墙在实际工程中应用奠定了必要的基础.

References)

[1]Bergman D M, Hanson R D. Viscoelastic mechanical damping devices tested at real earthquake displacements[J].EarthquakeSpectra, 1993, 9(3): 389-417.

[2]Cermac J E, Woo H G C, Lai M L, et al. Aerodynamic instability and damping on a suspension roof[C]//3rdAsia-PacificSymposiumonWindEngineering. Hong Kong,China,1994: 699-704.

[3]Crosby P, Kelly J M, Singh J P. Utilizing viscoelastic dampers in seismic retrofit of a thirteen-story steel framed building[C]//ProcASCEStructCongrⅫ.Atlanta,Georgia,USA, 1994: 1286-1291.

[4]Chang K C, Chen S J, Lai M L. Inelastic behavior of steel frames with added viscoelastic dampers[J].JournalofStructuralEngineering, 1996, 122(10): 1178-1186.

[5]Chang K C, Soong T T, Lai M L. Effect of ambient temperature on viscoelastically damped structure [J].JournalofStructuralEngineering, 1992, 118(7): 1955-1973.

[6]Min K W, Kim J, Lee S H. Vibration tests of 5-storey steel frame with viscoelastic dampers [J].EngineeringStructures, 2004, 26: 831-839.

[7]Soong T T, Dargush G F.Passiveenergydissipationsystemsinstructuralengineering[M]. New York: Wiley, 1997:2-20.

[8]Tan X M. Vibration control of structures with viscoelastic dampers[D]. Hong Kong, China: Department of Civil and Structural Engineering, Hong Kong Polytechnic University, 1998.

[9]李爱群.工程结构减振控制 [M].北京:机械工业出版社,2007:1-8.

[10]中华人民共和国建设部标准定额研究所.JG/T 209—2012建筑消能阻尼器[S].北京:中国标准出版社,2012.

Experiments of mechanical properties of super large viscoelastic damping wall under shear loading along transverse direction

Xu Junhong Li Aiqun

(School of Civil Engineering, Southeast University, Nanjing 210096, China)

To improve the accuracy of temperature dependence of viscoelastic damping device, the temperature scan experiments of viscoelastic material were conducted. Then, the system of shear loading along the transverse direction was put forward and the experiments of mechanical properties of “5+4” super large viscoelastic damping wall (VDW) were developed using this system. The curves of tanδ-T,G′-TandG″-Tof the viscoelastic material and the force displacement hysteretic curves were obtained through experiments. In addition, dynamical performance, such as the maximum damping force, loss factor, equivalent damping coefficient, storage stiffness, loss stiffness,loss modulus, storage modulus of VDW, were obtained. Results show that the loss factor (0.79) of viscoelastic material only slightly differ from the loss factor (0.77) of VDW, which proves that the “5+4” super large VDW has excellent damping properties under the system of shear loading along the transverse direction.

temperature scan; shear loading along the transverse direction; “5+4” viscoelastic damping wall; maximum damping force; loss factor

2014-09-08. 作者简介: 许俊红(1984—)，女，博士生；李爱群(联系人)，男，博士，教授，博士生导师，aiqunli@seu.edu.cn.

“十一五”国家科技支撑计划资助项目(2006BAJ03A04)、国家自然科学基金资助项目(51278104)、中建股份科技资助项目(CSCEC-2010-Z-01).

许俊红,李爱群.短轴向剪切加载模式下超大型黏弹阻尼墙力学性能试验[J].东南大学学报:自然科学版,2015,45(1):133-138.

10.3969/j.issn.1001-0505.2015.01.024

TU317.2

A

1001-0505(2015)01-0133-06