间接空冷系统变工况快速计算模型

马 欢 司风琪 李 岚 祝康平 阎文生

(1东南大学能源热转换及其过程测控教育部重点实验室, 南京 210096)(2中电神头发电有限责任公司, 朔州 036800)

间接空冷系统变工况快速计算模型

马 欢1司风琪1李 岚1祝康平2阎文生2

(1东南大学能源热转换及其过程测控教育部重点实验室, 南京 210096)(2中电神头发电有限责任公司, 朔州 036800)

以某600MW机组大型间接空冷系统为对象,分别建立了凝汽器热力计算模型与空冷塔数值计算模型,按照正交实验方法设计了49组工况,通过耦合迭代的方法对机组变工况运行进行了数值模拟,得到了相应的变工况运行特性信息．以所得数值模拟结果为样本,基于最小二乘支持向量机,建立了反映机组变工况运行特性的背压快速计算模型,在机组运行的全工况范围内反映了环境温度、侧风风速和热负荷变化对机组背压的影响．该方法结合了数值模拟方法机理建模的准确性和最小二乘支持向量机良好的泛化能力,计算高效,可为机组经济与安全运行提供连续定量的指导．

间接空冷系统;变工况;数值模拟;最小二乘支持向量机;背压

与常规湿冷系统相比,间接式空冷系统可大幅减少由于蒸发、风吹和排污所带来的汽水损失,在我国富煤贫水地区有很好的应用前景．间接空冷系统是一个由凝汽器、泵与输水管道、空冷塔等构成的封闭系统,其热力性能容易受到机组负荷及外界环境的影响．机组背压是反映机组运行状况的综合指标[1],研究间接空冷系统变工况运行性能,掌握机组背压的变化规律,对于机组安全性与经济性运行具有重大意义．

现场试验[2]是获得机组变工况运行特性的有效途径,但是由于间接空冷系统对象尺度大且复杂,造成现场试验工作量大且成本高,而且外界环境条件往往不可控,因此限制了试验研究的效果．数值模拟方法以详细的物理过程为基础,通过数值计算可以较好地模拟出过程运行特性,设置不同的初始条件,可以得到相应负荷和环境条件下的系统特性,因此引起了研究者们的广泛关注．为获得间接空冷系统变工况运行特性,张春雨等[3]建立了哈蒙式间接空冷系统凝汽器压力变工况数学计算模型,分析了影响系统运行性能的因素,为提高系统性能提供了理论依据．文献[4-6]还建立了间接空冷系统变工况运行特性的数值计算模型,以变工况数值计算为基础,分析了机组背压的变化规律．

大型间接式空冷系统是一个大物理尺度的复杂对象,机组运行与影响因素间存在很强的非线性关系．若要定量地研究机组全工况运行特性,单纯地使用数值模拟手段从时间和连续性考虑是不可取的．支持向量机(SVM)是一种非常有力的机器学习方法,具有出色的泛化能力,被广泛地用于复杂非线性系统的建模中[7]．最小二乘支持向量机(LSSVM)是向量机的改进,降低了求解难度,提高了运算速度[8]．

本文以某600MW机组间接空冷系统为对象,分别建立了空冷塔特性模型和凝汽器热力计算模型,通过两者耦合进行了机组冷端变工况特性的模拟,并与现场运行数据进行对比,验证了数值模型的正确性．然后，采用正交试验方法设计了49组模拟工况,并以模拟结果为样本,建立了基于LSSVM的机组背压快速计算模型,研究分析了机组热负荷、环境温度和侧风速度对背压的影响．该模型结合了数值模拟机理建模的准确性和最小二乘支持向量机良好的泛化能力,具有良好的工程应用价值．

1 数值计算模型

1.1 哈蒙式间接空冷系统

哈蒙式间接空冷系统汽水流程如图1所示.循环冷却水从凝汽器中吸热后进入空冷塔冷却,完成对排汽吸热和对空气放热的循环．

空冷塔内的流动是惯性力、压力、黏性力和浮力的动态平衡,与传热相互影响,紧密相连．

对塔内的三维流动及传热可做以下假设:

1) 稳态模拟,各参数不随时间变化.

2) 空气是干燥的、不可压缩的理想气体[9].

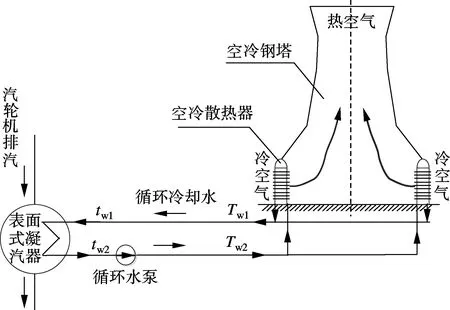
图1 哈蒙式间接空冷系统结构图

3) 用Boussinesq假设来处理浮力的影响[10]．

根据上述假设,可通过下式来描述空气侧流动及传热:

·V=0

(1)

ρ(V·)V=-p+τ-ρβ(T-Tref)g+Sh

(2)

ρ(V·)T=

(3)

ρ(V·)k=

(4)

ρ(V·)ω=

(5)

式中,V,ρ,P,μ,μt和τ分别表示速度矢量、密度、压力、层流黏度、湍流黏度和切应力;β为空气膨胀率;g为重力加速度;层流普朗特数Pr=0.71,湍流普朗特数Prt=0.75;Sh,Qh为动量方程和能量方程的源项，只存在于散热器区域内的动量和能量方程中;T,Tref为环境温度和参考温度;k为湍流动能;ω为耗散率;Gk为由平均速度梯度产生的湍流能;Gω为由耗散产生的湍流能;Yk,Yω分别为湍流动能和耗散率的损耗;Dω为交叉扩散项;σk,σω分别为湍流动能和耗散率对应的普朗特数．

空气经过散热器的压降与流体动压成正比,即

(6)

式中,vn为通过散热器速度的垂直分量;kn为无量纲压损系数．

空气流经散热器管束的对流换热量为

Qa=Aah(Tw-T)

(7)

式中,Aa为空冷散热器面积;h为空冷散热器传热系数;Tw为进出塔水温的平均值．

凝汽器主凝结区的蒸汽凝结温度为

(8)

式中,tw1为凝汽器进水温度;Ac为凝汽器有效面积;K为凝汽器传热系数[11]；Dw为冷却水量;cw为水的比热;Δt为冷却水温升．

根据凝汽器热平衡方程可得

(9)

式中,Dc为进入凝汽器的蒸汽量;f(ts)为对应水温ts下的汽化潜热.

在式(8)、(9)构成的方程组中,Ac为已知,Dc,Dw在特定工况下为定值,tw1为自变量,ts为因变量,对应饱和压力Ps可由水蒸气物性求得，Ps近似为凝汽器压力Pc,也近似于机组背压PB．

稳定工况下,凝汽器的放热量与空冷塔对循环水的冷却量相等,循环水进出凝汽器的温度tw1,tw2分别与出进空冷塔的水温Tw2,Tw1相等，且均保持不变．当机组运行参数波动时,上述平衡关系被破坏,因而上述模型无法直接用于机组的变工况计算．本文使用耦合迭代模拟法,流程图如图2所示.通过截取机组过程变化数据并假定其处于稳态进行模拟,根据得到的结果再进行稳态判定,然后输出最终状态,得到变工况下的运行参数．

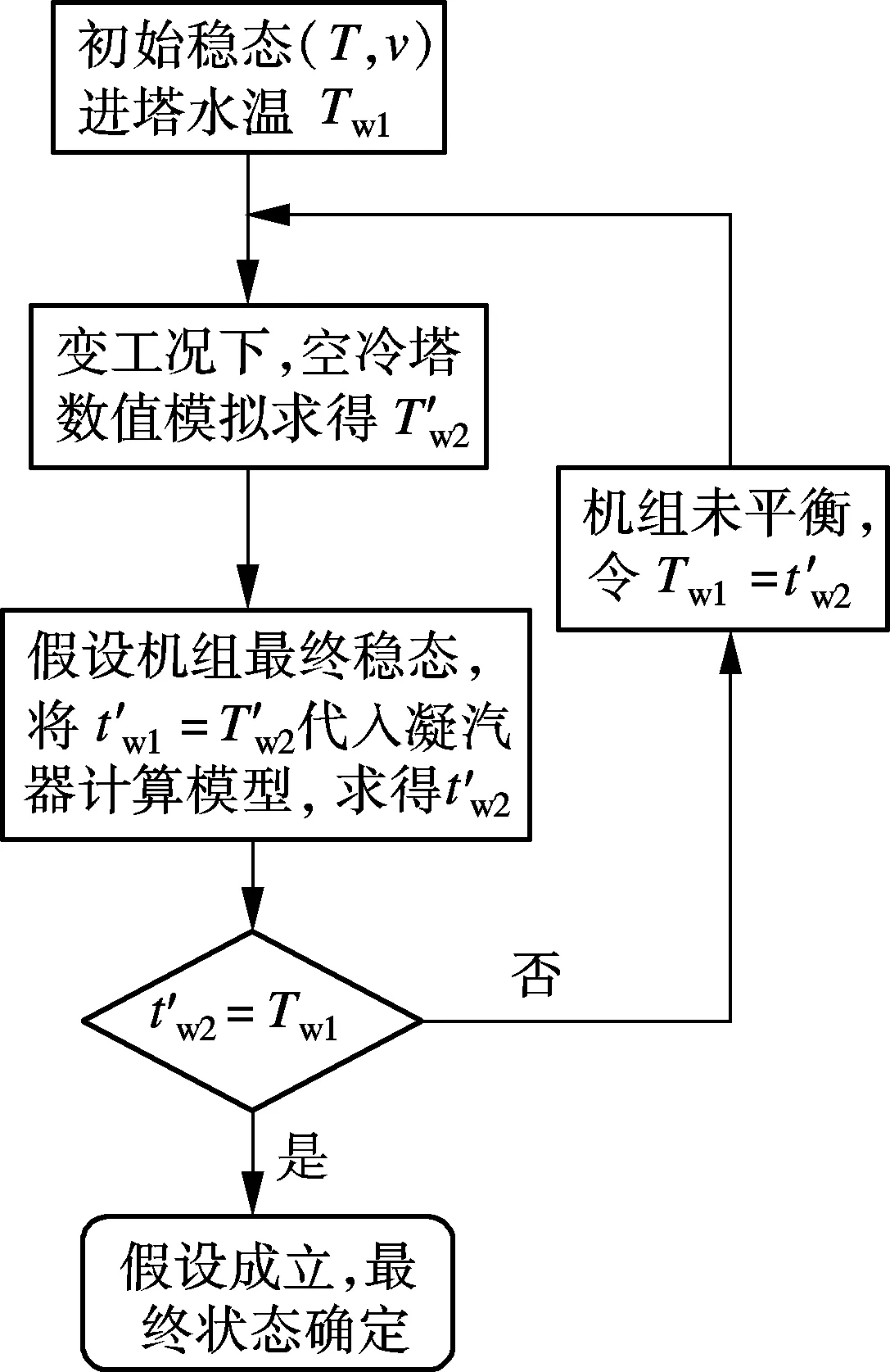
图2 耦合迭代法流程图

1.2 对象模型

本文以某600MW超临界间接空冷机组为研究对象,其中凝汽器为哈蒙式N-35000型;冷却面积为35000m2;流程数和壳体数为1∶2;冷却水管材为TP304不锈钢，管径24mm，壁厚0.5mm;设计流速为2.3m/s．

空冷塔为钢筋混凝土双曲线薄壳式风筒空冷塔,散热器在其外围垂直布置,空冷塔的几何尺寸如表1所示．该机组的空冷塔还兼作锅炉排烟及脱硫设施的布置场地,即具有三合一功能,如图3所示．根据散热器实验报告可得空冷散热器压损系数和传热系数为

(10)

(11)

表1 空冷塔结构尺寸表 m

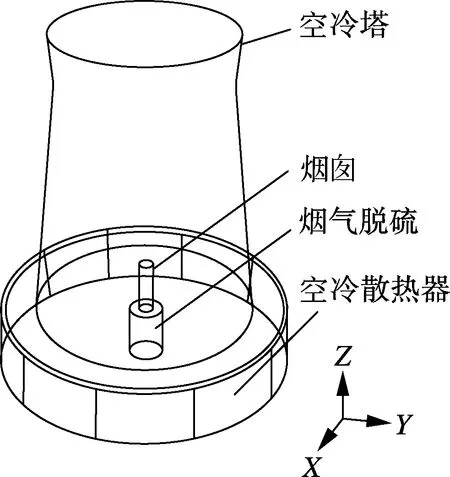
图3 空冷塔示意图

计算区域如图4所示,采用非结构化四面体和结构化六面体相结合的网格方式对区域进行多区块划分,在保证计算精度的同时减少网格总数．进口面在无风时为压力进口边界,有侧风时为速度进口边界,进口面风速采用幂指数风速廓线计算公式[12],计算不同高度的风速值．计算区域出口为压力出口边界,指定所给温度和速度下的湍流动能和湍流耗散率．地面和塔壁取壁面边界,绝热无滑移．

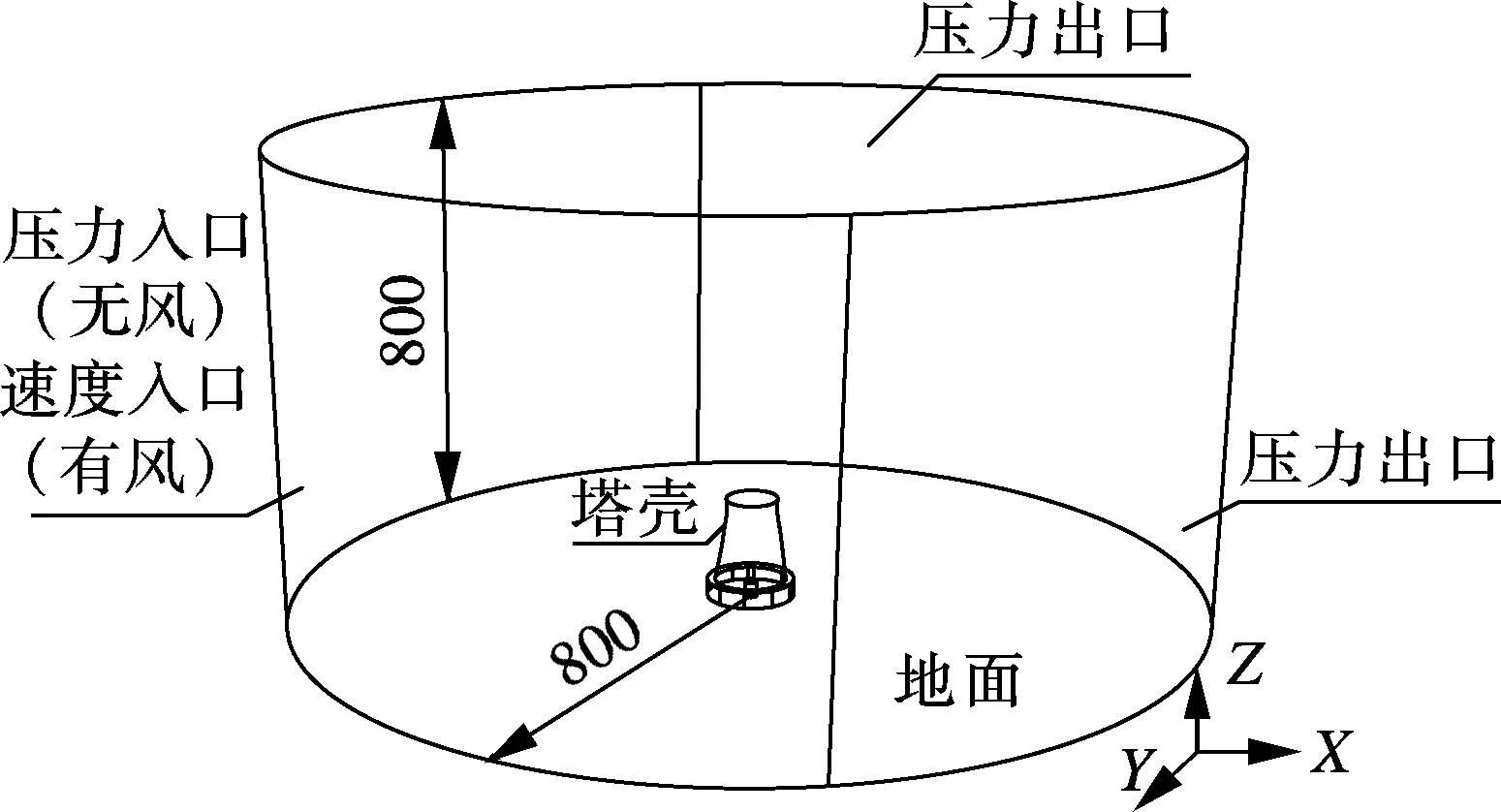
图4 计算区域示意图(单位:m)

1.3 正交模拟实验设计

一般可认为机组背压主要受到排汽量Dc、循环水量Dw、环境温度T和侧风风速v变化的影响．而在夏季或冬季运行过程中,循泵一般不随意启停,因此主要考虑Dc,T和v三因素的影响．本文按照“三因素七水平”正交实验设计[13],采用正交表L49(78)安排模拟实验,共计49组,部分实验安排如表2所示．表中，ε表示热负荷率,为实际运行与额定负荷下排汽量之比．

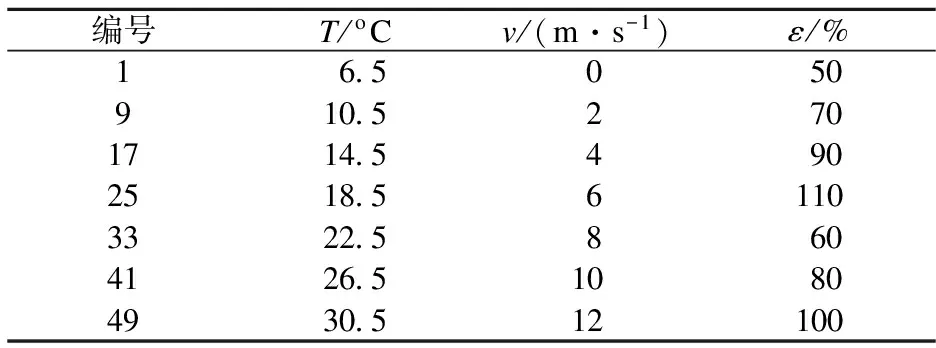
表2 模型变量及部分模拟实验工况

2 机组变工况特性计算模型

2.1 最小二乘支持向量机

SVM通过结构风险最小化原理来提高泛化能力,可较好解决小样本、非线性、高维数等实际问题． LSSVM是向量机的改进,通过选取不同的损失函数,将SVM的二次规划问题转变为求解线性方程的问题,加快了收敛速度,更适用于工程应用,可较好地实现实时建模与模型修正．对于给定训练数据集(xi,yi),其中,i=1,2,…,m,xi∈Rn为模型输入量,yi∈R为模型输出量．选择一非线性映射φ(·)，将样本从原空间Rn映射到高维特征空间,从而实现输入空间中的非线性回归转化为高维特征空间中的线性回归．根据结构风险最小化原理,回归问题可表示为约束优化问题，即

(12)

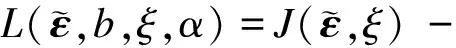
(13)

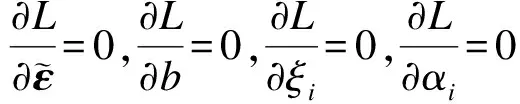
定义核函数K(xi,xj)=φ(xi)·φ(xj),将优化问题转化为求解线性方程组，即

(14)

通过最小二乘法求出回归系数αi和偏差b,得到如下非线性计算模型：

(15)

2.2 计算模型

本文选取正交实验模拟结果为训练数据,建立了基于LSSVM的机组背压快速计算模型.将环境温度T、侧风风速v和热负荷率ε作为模型输入变量,将机组背压PB作为输出变量,通过观察背压可了解机组的运行状态,为进一步运行决策提供指导．

将样本数据按下式进行归一化处理：

(16)

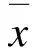
核函数选用如下径向基核函数：

K(x,xi)=exp(-‖x-xi‖2/(2σ2))

(17)

式中,σ为核宽度．

模型性能评价指标采用如下的平均误差计算公式:

(18)

为了验证模型的准确性,本文从厂级监控信息系统(SIS)中选取10组工况进行了数值模拟,并以此为LSSVM的测试样本,详细工况见表3．

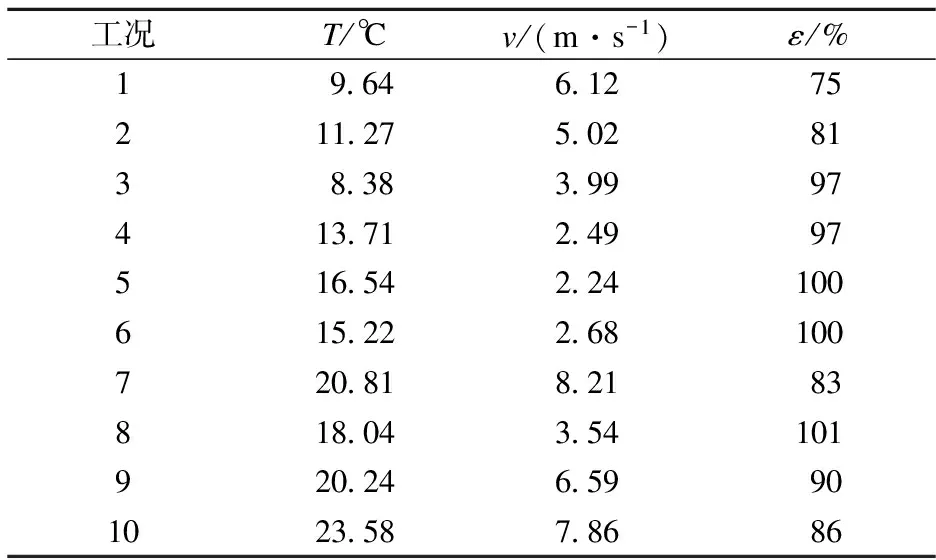
表3 部分运行工况信息

综合考虑模型精度与平滑度,由单纯形法[14]优化选择模型参数C=2955,σ=22.5,得到模型平均训练误差γ=1.69%.将测试样本输入到训练好的模型中,结果如表4所示.由表可见，计算值与模拟值相近,由式(18)得到的平均泛化误差γ=2.41%．通过对比背压的实际运行值,得到数值模型的最大误差和平均误差分别为8.47%和4.76%,快速计算模型的最大误差和平均误差分别为6.92%和4.50%．可见基于LSSVM的机组背压快速计算模型并未造成误差累计,反而使最大误差减小了．这得益于结构风险最小化的特性,使其具有良好的泛化能力,能够在变工况下准确计算背压．

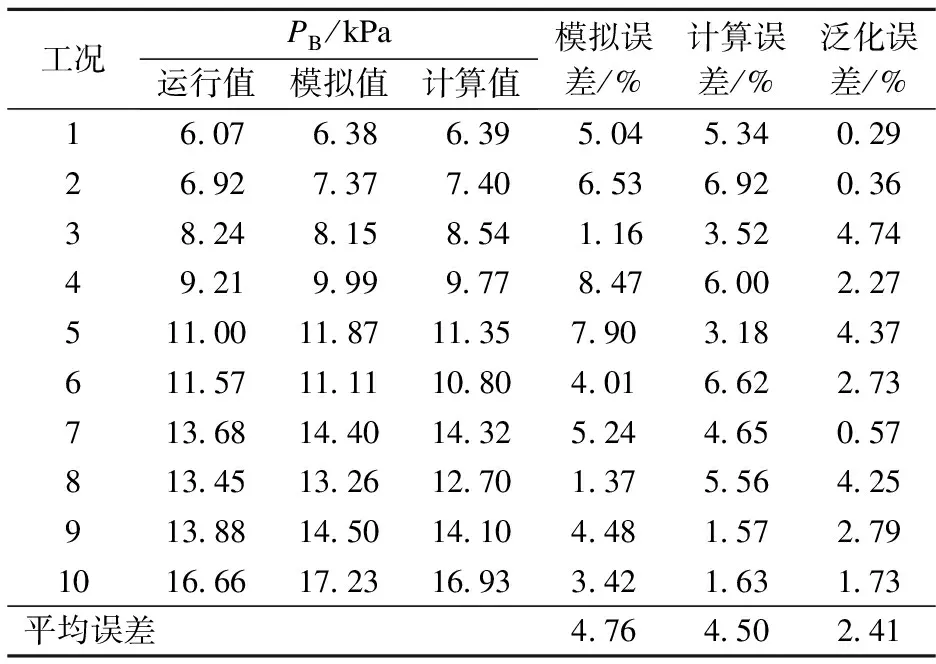
表4 背压快速计算模型的校验

本文中建模的计算机为戴尔T7600工作站,2GHz主频,64GB内存．使用数值模拟完成1个工况需8h,而利用最小二乘支持向量机完成1个工况输出仅需10s．本文将两者相结合,首先利用数值模拟机理建模的特性,取得可靠的小样本数据,其次基于此样本数据,利用最小二乘支持向量机良好的泛化能力建模,满足工程应用的快速性与连续性．针对间接空冷系统,相比单纯的数值模拟,本文方法有着更快的计算效率，可定量连续快速地为机组运行提供实时指导．

2.3 机组变工况分析

图5为机组背压与2个不同影响因素的曲面图．图6为机组背压与不同影响因素的关系.由图5(a)和图6(a)可知,随着环境温度的升高,机组背压明显增大．这是由于环境温度升高使得空冷散热器传热温差下降,传热恶化,出塔水温升高．凝汽器进水温度上升削弱了凝汽器传热性能,导致机组背压升高．由图5(b)和图6(b)可知,机组背压随着负荷的增加而增大．这是因为机组升负荷时排汽量增加,总散热量增加,使得机组排汽温度上升,背压上升．由图5(c)和图6(c)可知,风速在0～12m/s的范围内,机组背压随着侧风风速的增大而增大,这是因为风速的变化改变了空冷塔及周围流场．风速增大减少了进塔空气量[5],削弱了空冷塔的散热性能,由于空冷塔及凝汽器的耦合作用,从而使得机组背压增大．由图5(a)、(c)可得,在相同变化率下,风速对背压的影响要小于环境温度和热负荷的影响．

(a) 环境温度与侧风风速的影响(ε=80%)

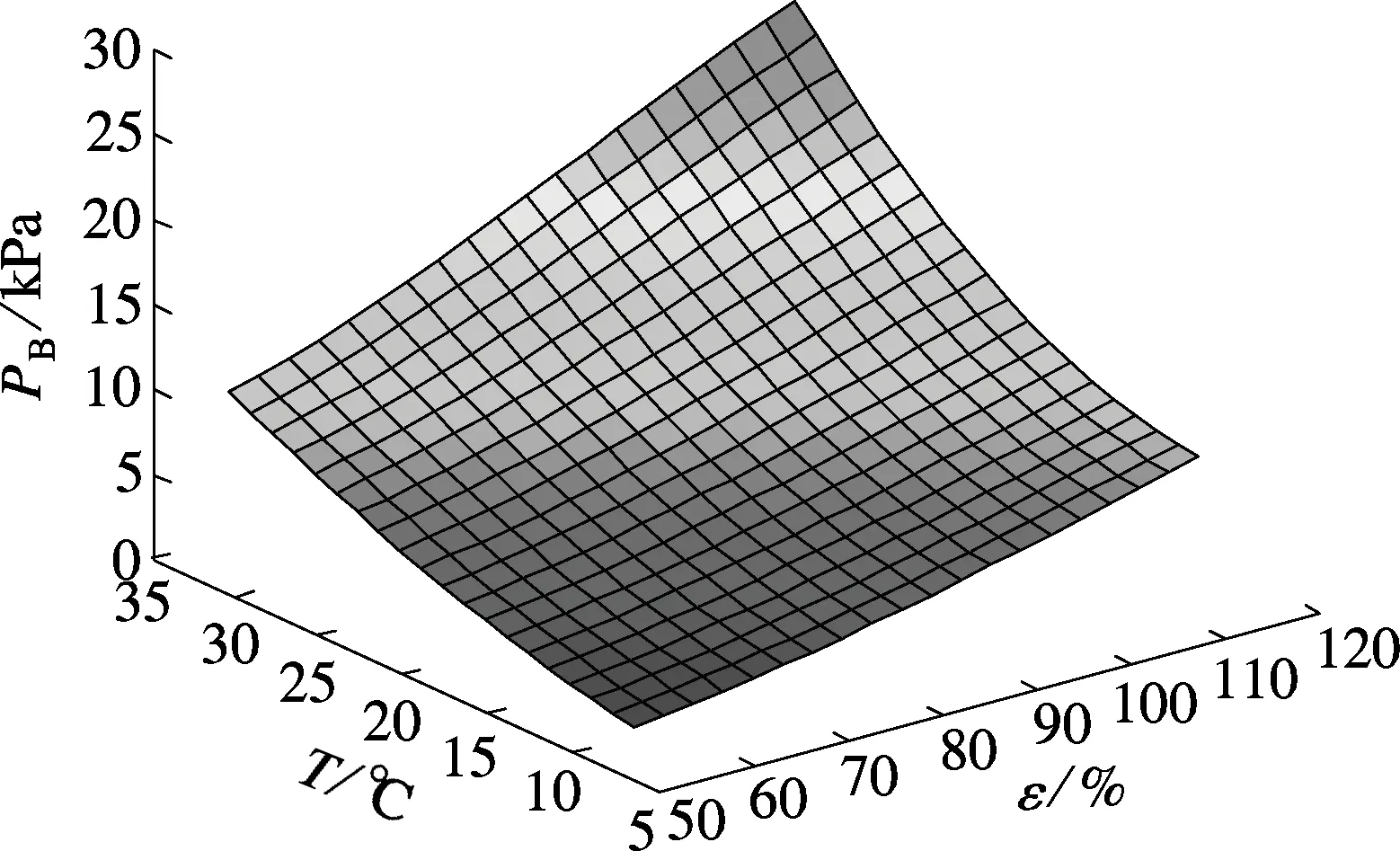
(b) 热负荷与环境温度的影响 (v=4m/s)

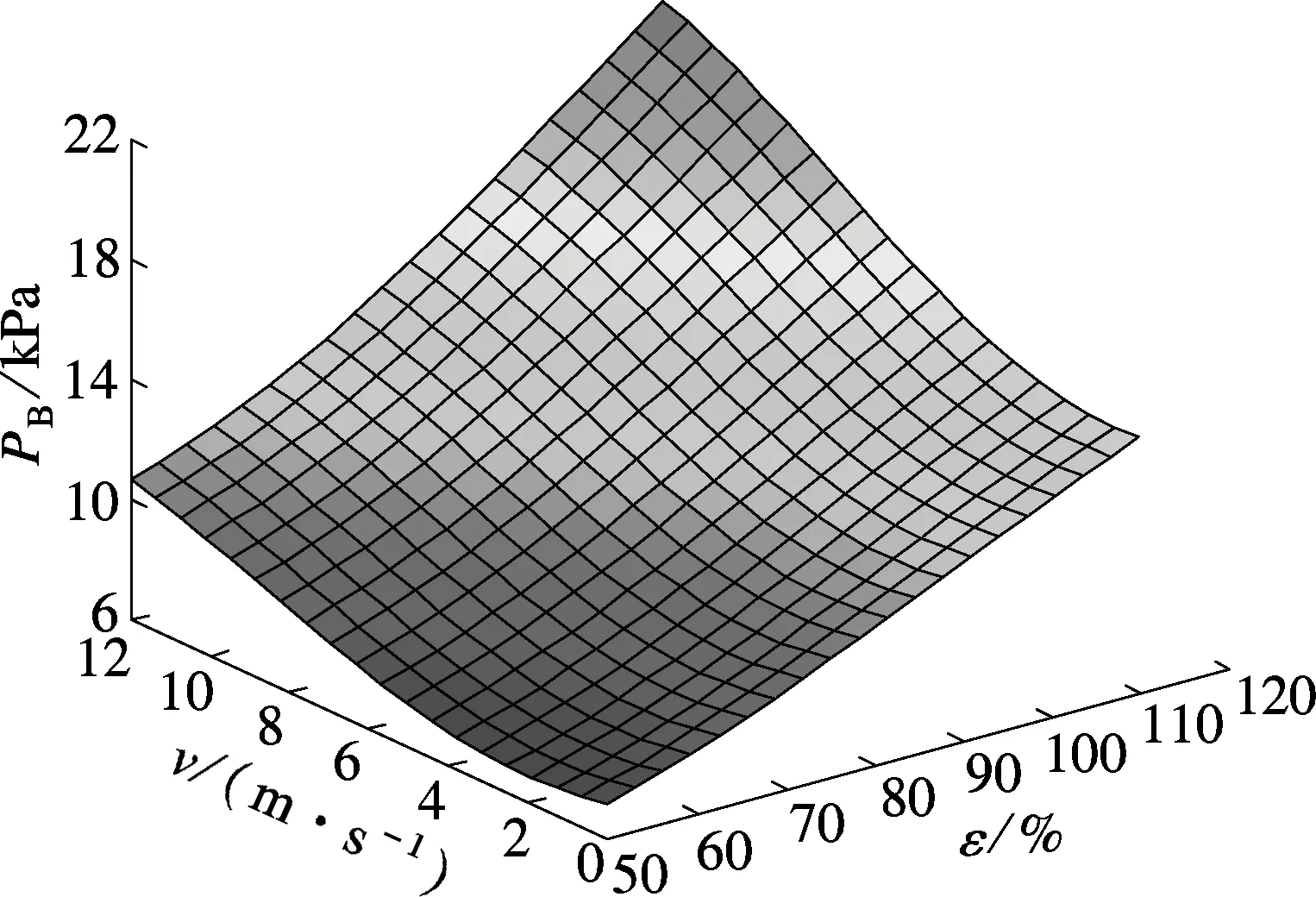
(c) 侧风风速与热负荷的影响 (T=20℃)

环境温度和侧风风速是自然因素,不可人为控制,而本文所建机组背压快速计算模型可有效地计算出给定环境下,机组安全运行的热负荷区间,对机组实际运行操作具有重大意义．

3 结论

1) 本文以某600MW超临界间接空冷机组为例,通过耦合凝汽器与空冷塔系统,建立了机组冷端数值计算模型．通过正交实验法科学安排模拟工况,完成了对机组变工况运行的数值模拟．

2) 以数值模拟数据为样本,建立了基于最小二乘支持向量机的机组背压快速计算模型．通过与实际运行数据和模拟结果相比,该模型可准确计算不同工况下机组运行背压．

3) 模型计算表明，机组背压随环境温度、侧风风速和热负荷任一因素的增加而升高.相对环境温度和热负荷,侧风风速对机组的影响较小．

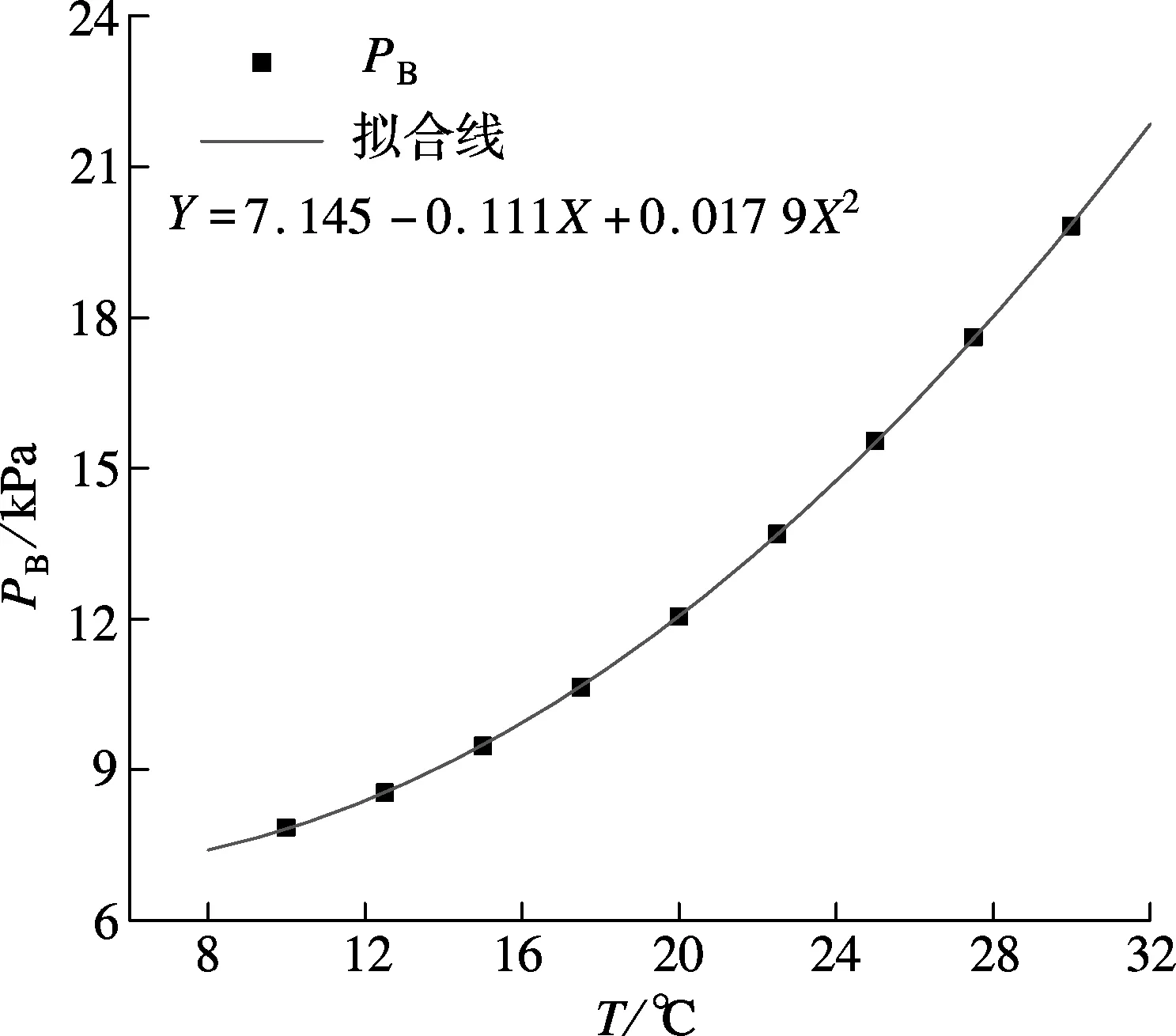
(a) 背压与环境温度的关系 (v=3m/s, ε=90%)

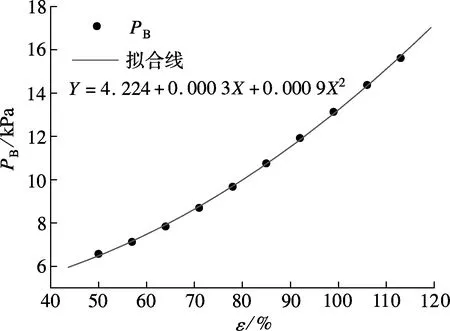
(b) 背压与热负荷的关系 (T=16℃, v=7m/s)

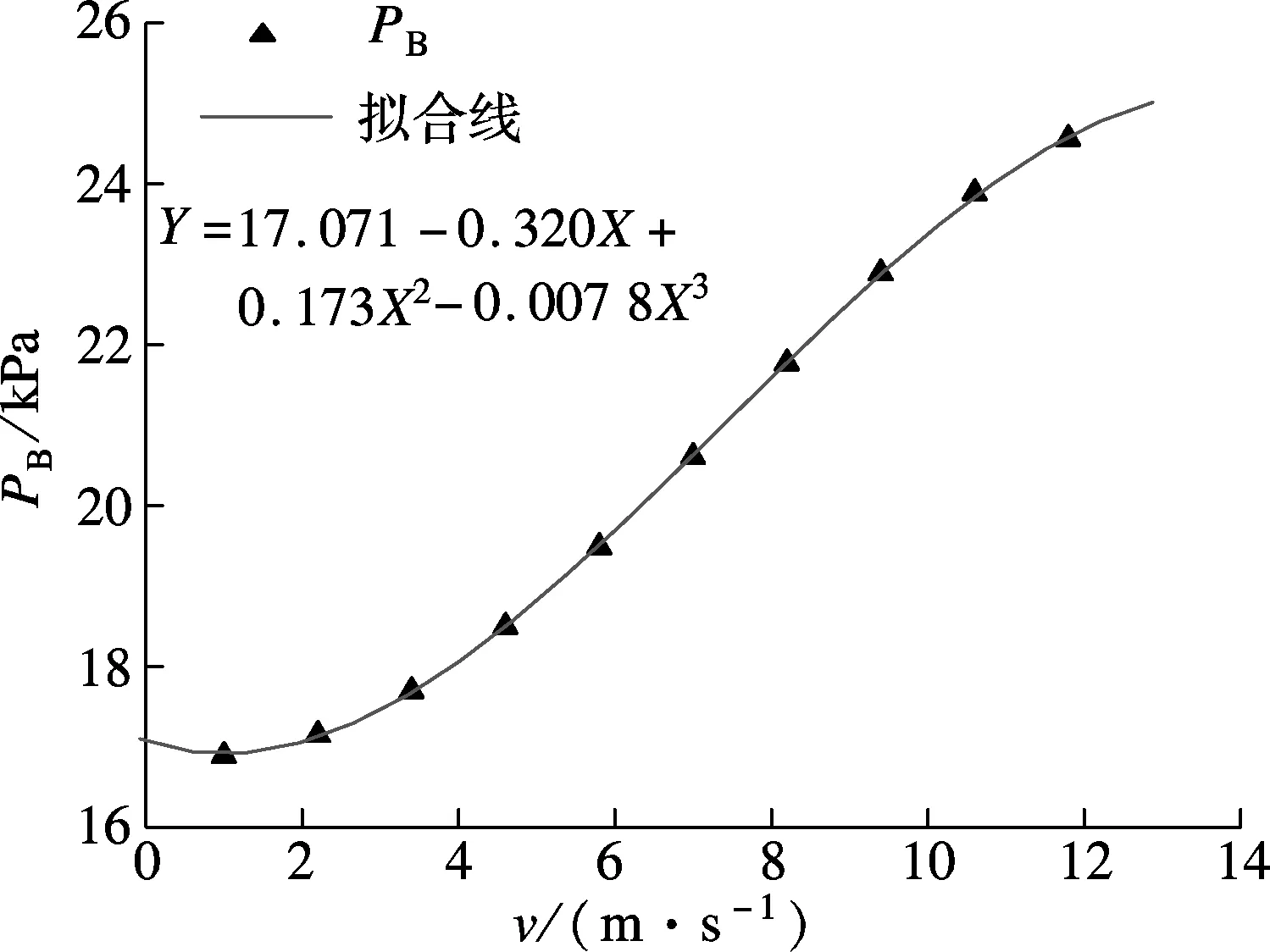
(c) 背压与侧风风速的关系 (T=25℃, ε=100%)

4) 本文模型结合了数值模拟机理建模的准确性和最小二乘支持向量机良好的泛化能力,可为机组经济性与安全性运行提供连续定量指导,并为同类型机组变工况运行特性的研究提供了一种新技术手段．

References)

[1]杨立军,杜小泽,杨勇平.空冷凝汽器全工况运行特性分析[J].中国电机工程学报,2008,28(8):24-28. Yang Lijun,Du Xiaoze,Yang Yongping.Performance analysis of air-cooled condensers at all operating conditions[J].ProceedingsoftheCSEE, 2008, 28(8): 24-28.(in Chinese)

[2]Du Preez A F,Kröger D G.The effect of the heat exchanger arrangement and wind-break walls on the performance of natural draft dry-cooling towers subjected to cross-winds[J].JournalofWindEngineeringandIndustrialAerodynamics,1995, 58(3):293-303.

[3]张春雨,严俊杰,李秀云.哈蒙式间接空冷系统变工况特性的理论研究[J].动力工程,2000,20(1):566-570. Zhang Chunyu,Yan Junjie,Li Xiuyun. Theoretical research on part load operation performance of Hamen indirect air-cooled system[J].JournalofPowerEngineering, 2000, 20(1):566-570.(in Chinese)

[4]卜永东,杨立军,杜小泽,等.电站空冷系统变工况性能的数值研究[J].中国电机工程学报,2012, 32(35):66-73. Bu Yongdong,Yang Lijun,Du Xiaoze,et al.A numerical approach to off-design performance of dry cooling systems in power plants[J].ProceedingsoftheCSEE, 2012, 32(35):66-73.(in Chinese)

[5]Yang L J,Wu X P,Du X Z,et al.Dimensional characteristics of wind effects on the performance of indirect dry cooling system with vertically arranged heat exchanger bundles[J].InternationalJournalofHeatandMassTransfer, 2013, 67:853-866.

[6]孔令华.空冷机组冷端系统运行特性分析及优化[D].北京:华北电力大学能源动力与机械工程学院,2008.

[7]李瑾,刘金朋,王建军.采用支持向量机和模拟退火算法的中长期负荷预测方法[J]. 中国电机工程学报,2011,31(16):63-66. Li Jin,Liu Jinpeng,Wang Jianjun.Mid-long term load forecasting based on simulated annealing and SVM algorithm[J].ProceedingsoftheCSEE, 2011,31(16):63-66.(in Chinese)

[8]de Brabanter K,Karsmakers P,de Brabanter J,et al.Confidence bands for least squares support vector machine classifiers:A regression approach[J].PatternRecognition, 2012, 45(6):2280-2287.

[9]Al-Waked R,Behnia M.The effect of windbreak walls on the thermal performance of natural draft dry cooling towers[J].HeatTransferEngineering, 2005, 26(8):50-62.

[10]Goodarzi M,Amooie H.A proposed heterogeneous distribution of water for natural draft dry cooling tower to improve cooling efficiency under crosswind[C]//IEEE4thConferenceonThermalPowerPlants.Tehran,Iran,2012:1-6.

[11]西北电力设计院.电力工程水务设计手册[M].北京:中国电力出版社,2005:122-123.

[12]Yang L J,Chen L,Du X Z,et al.Effects of ambient winds on the thermo-flow performances of indirect dry cooling system in a power plant[J].InternationalJournalofThermalSciences,2013, 64:178-187.

[13]任露泉.试验设计及其优化[M].北京:科学出版社,2009:13-25.

[14]敖特根.单纯形法的产生与发展探析[J].西北大学学报:自然科学版,2012,42(5):861-864. Ao Tegen.Analysis of the formation and development of the simplex method[J].JournalofNorthwestUniversity:NaturalScienceEdition, 2012, 42(5):861-864.(in Chinese)

Fast calculation model of indirect air-cooled system under off-design condition

Ma Huan1Si Fengqi1Li Lan1Zhu Kangping2Yan Wensheng2

(1Key Laboratory of Energy Thermal Conversion and Control of Ministry of Education, Southeast University, Nanjing 210096, China) (2China Power Shentou Power Generating Co.,Ltd., Shuozhou 036800, China)

Taking a 600MW indirect air-cooled unit as an example, thermal calculation model of the condenser and numerical calculation model of air-cooled tower are established, respectively. In order to obtain operating characteristics of the indirect air-cooled system under off-design condition, 49 numerical simulations were carried out with the coupled method according to orthogonal experimental design. Based on least square support vector machine, a fast calculation model for back pressure which reflects operating characteristics of the unit is established based on the results of numerical computation. By this model, the effects of ambient temperature, crosswind speed and thermal load on back pressure of the unit are obtained under all working conditions. Combining the accuracy of numerical simulation based on mechanism and excellent generalization of least square support vector machine, this model has fast calculation speed and provides a continuous and quantitative guidance for the economic and safe operation of the unit.

indirect air-cooled system; off-design condition; numerical simulation; least square support vector machine; back pressure

2014-07-24. 作者简介: 马欢(1991—)，男，博士生；司风琪(联系人)，男，博士，教授，博士生导师，fqsi@seu.edu.cn.

国家自然科学基金资助项目(51176030)、中电国际科技计划资助项目(2013-006-ZDG-KJ-X).

马欢,司风琪,李岚,等.间接空冷系统变工况快速计算模型[J].东南大学学报:自然科学版,2015,45(1):79-84.

10.3969/j.issn.1001-0505.2015.01.015

TK264

A

1001-0505(2015)01-0079-06