基于网格变形与代理模型的横梁参数化建模与轻量化优化

罗 黎 孙蓓蓓 陈翰翔

(东南大学机械工程学院, 南京 211189)

基于网格变形与代理模型的横梁参数化建模与轻量化优化

罗 黎 孙蓓蓓 陈翰翔

(东南大学机械工程学院, 南京 211189)

建立了包含导轨结合面的横梁有限元模型,并通过模态实验验证了有限元模型的正确性,在多种极限工况下对原横梁进行了静动态特性分析与评价;针对现有优化方法的不足,采用了一种新的优化设计方法:通过网格变形技术实现结构尺寸的参数化建模,基于拉丁超立方采样、相对灵敏度分析和Kriging近似模型建立横梁结构优化的代理模型以代替现有的有限元仿真模型;以体积最小为优化目标,以刚度、强度和动态性能不变为约束条件,采用遗传算法进行优化设计．优化结果表明:在保持横梁最大变形、静刚度以及一阶模态频率基本不变的情况下,横梁总质量减少了58 kg(减少了5.9%)．

参数化;网格变形技术;轻量化;代理模型

数控转塔冲床是一种加工多孔薄板的冲裁设备,横梁是数控转塔冲床的送料机构,其动态响应性能直接关系到送料的准确性,同时也影响板材的加工精度和送料速度.随着数控转塔冲床工作速度的提高,横梁的轻量化成为保证加工精度和高速度的必然要求．

目前,国内外轻量化设计主要有3种途径[1]:合理采用质量较轻或刚度较高的金属或非金属材料[2]、对原有结构进行优化改进及基于先进控制技术的系统轻量化设计．

横梁轻量化的关键是建立准确的有限元模型,由于冲床横梁结构复杂,各部件间存在大量结合面,传统的建模方法忽略结合面的影响,将各部件间进行刚性连接,这与实际结构存在较大的误差. 在现有工程优化方法中,大多直接将仿真模型与优化算法耦合,这通常会导致优化过程的低效,因为优化迭代中仿真分析需要消耗大量的计算成本[3],此外,优化中有限元网格会产生穿透和单元质量问题,使得单次仿真失效而导致整个优化过程的终止．

针对以上问题,本文采用一种全新的集成优化设计方法, 在建立各部件准确的结合面模型基础上,利用网格节点的移动与变形实现横梁结构的参数化有限元建模,将壁厚和实体结构尺寸同时取为设计变量,运用拉丁超立方技术对设计变量进行采样和灵敏度分析,筛选掉对横梁性能影响较小的设计变量,建立基于Kriging近似模型的优化代理模型,并采用遗传算法(GA)实现横梁轻量化优化设计,取得了较好的轻量化设计效果．

1 横梁有限元模型的建立与静动态特性分析

1.1 几何模型与网格划分

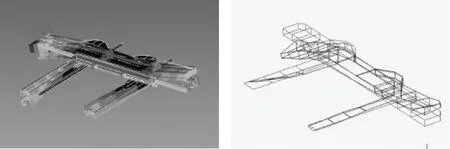
如图1所示,数控转塔冲床横梁主要由横梁方管、滚珠丝杠传动系统、电机、轴溜板、护罩等组成,横梁通过电机带动滚珠丝杠实现加工板材沿X,Y方向进给运动．

利用CAD软件Solidworks对几何模型进行简化处理:忽略工艺上的倒角和倒圆以及连接用的小直径孔;为了提高计算精度与速度,对薄板结构(L/H>10,L为板长,H为板高)进行抽壳处理;为了避免划分的网格出现畸形和结构模型出现病态,合并位置较近的节点．由于机床横梁整体结构较大,为了提高有限元模型的计算精度,节省计算时间与空间,将实体结构划分为六面体网格,薄板结构划分为四边形面网格．

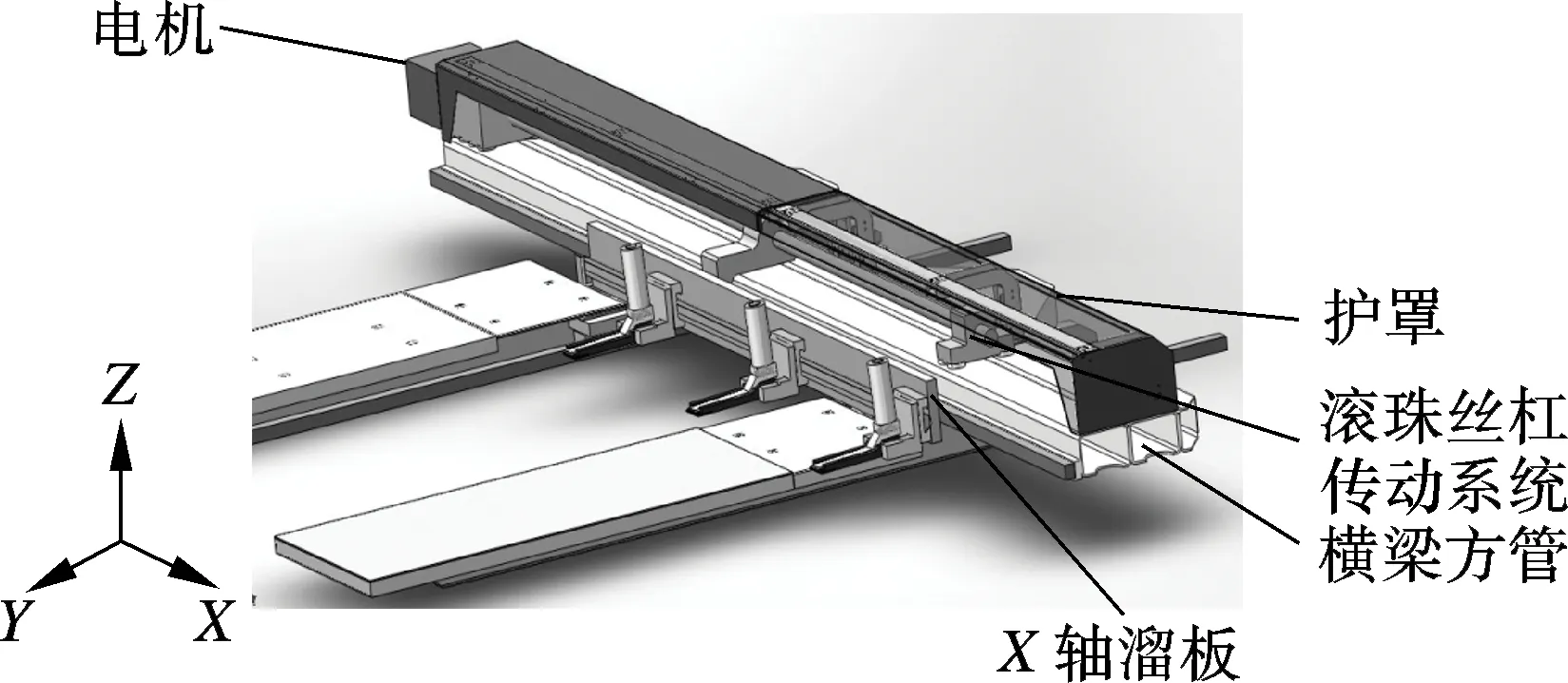
图1 横梁三维CAD模型

1.2 连接方式及边界条件的确定

机床常用的连接方式主要有焊接、铆接、螺栓连接等,此外机床上存在大量的结合面,如滚动导轨结合面．本文主要考虑焊接、滚动导轨结合面这2种连接方式,在Hyperworks软件中可以通过CWELD单元、CELAS1弹簧单元来实现,该数控转塔冲床横梁各部件连接方式如表1所示．

横梁主要通过Y进给方向导轨与机身相连,故在有限元中约束导轨底部6个方向自由度,与实际情况相符．

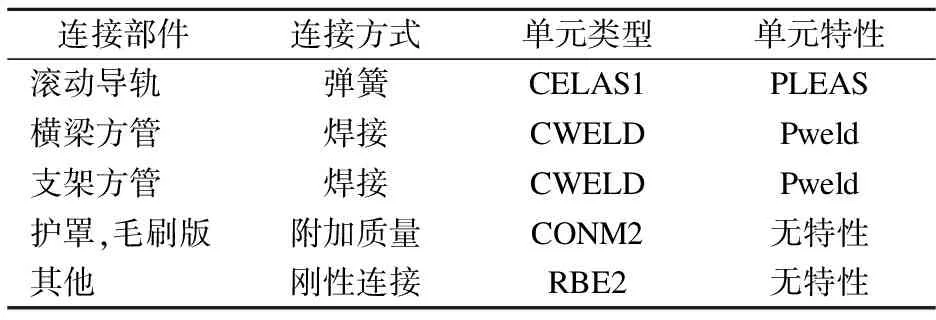
表1 横梁各部分连接方式

1.3 导轨结合面参数识别

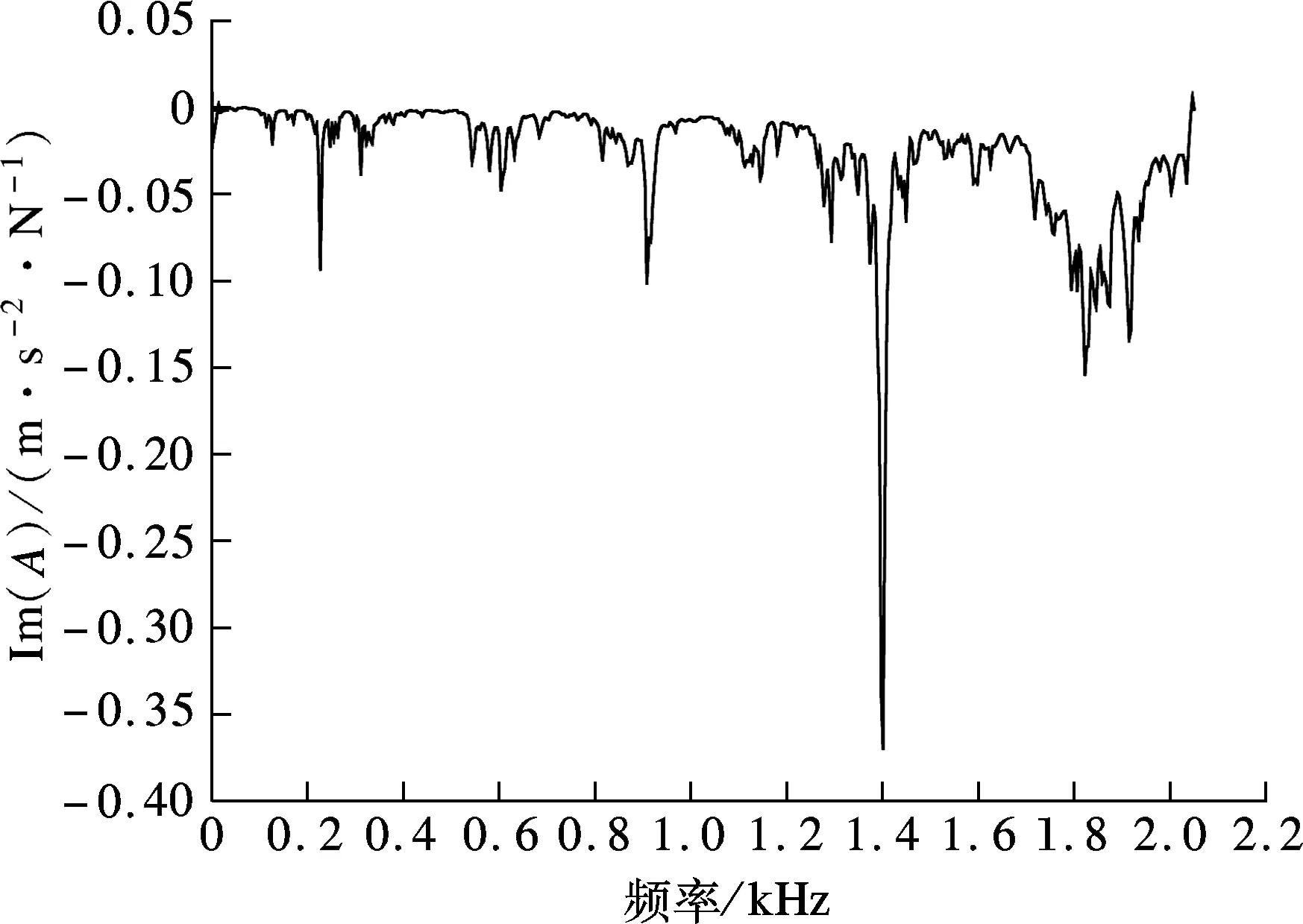
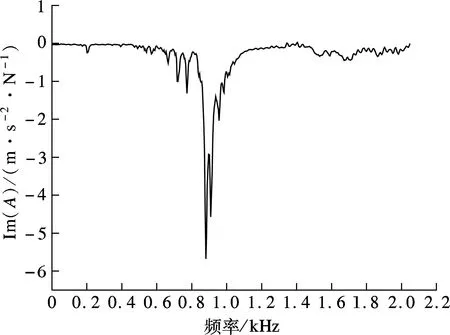
研究表明[4],机床中结合部接触刚度约占整机总刚度的 60%,结合部接触阻尼约占整机总阻尼的90%.机床结合部很大程度上影响了整机的动力学特性,模型中是否考虑结合面,其计算结果相差几倍甚至几十倍,因此本文考虑了结合面这一因素.实验测试是获取结合面参数最有效的方法,图2分别为Y,X方向导轨实频和虚频特性曲线,图中，A为幅值.在实频特性曲线的拐点处(即与频率轴交点处)可以确定出该阶模态的共振频率wn,根据机械振动理论可知

(1a)

ζ=(c/2)Mwn

(1b)

(1c)

式中,K为接触刚度;M为滑块质量;ζ为模态阻尼比;c为接触阻尼．

通过计算得到滚动导轨结合面接触参数,如表2所示．

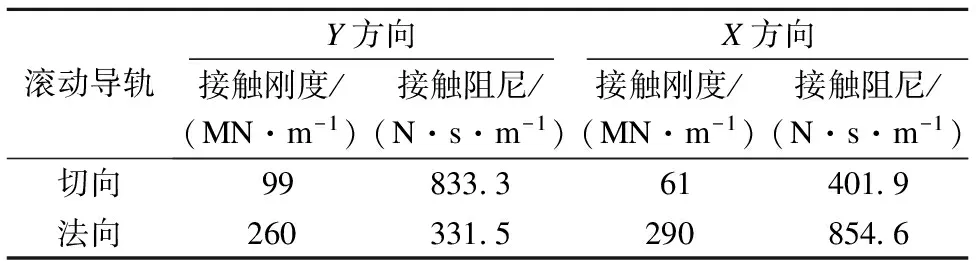
表2 滚动导轨接触面刚度和阻尼参数

1.4 横梁有限元模态分析

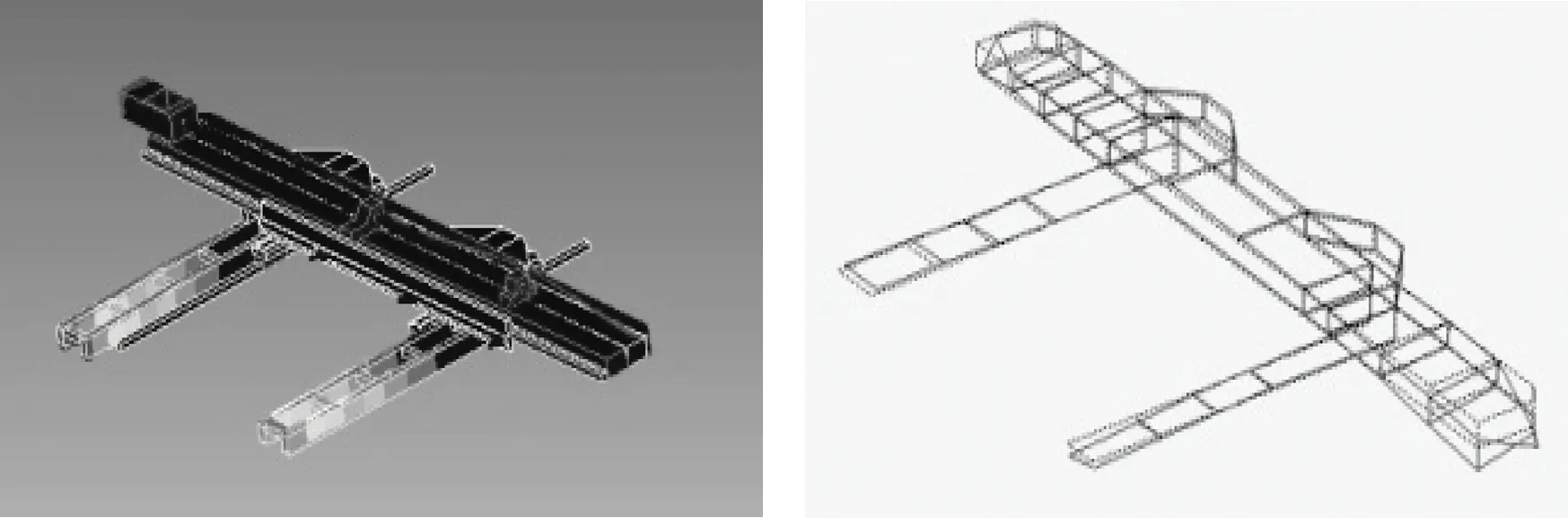
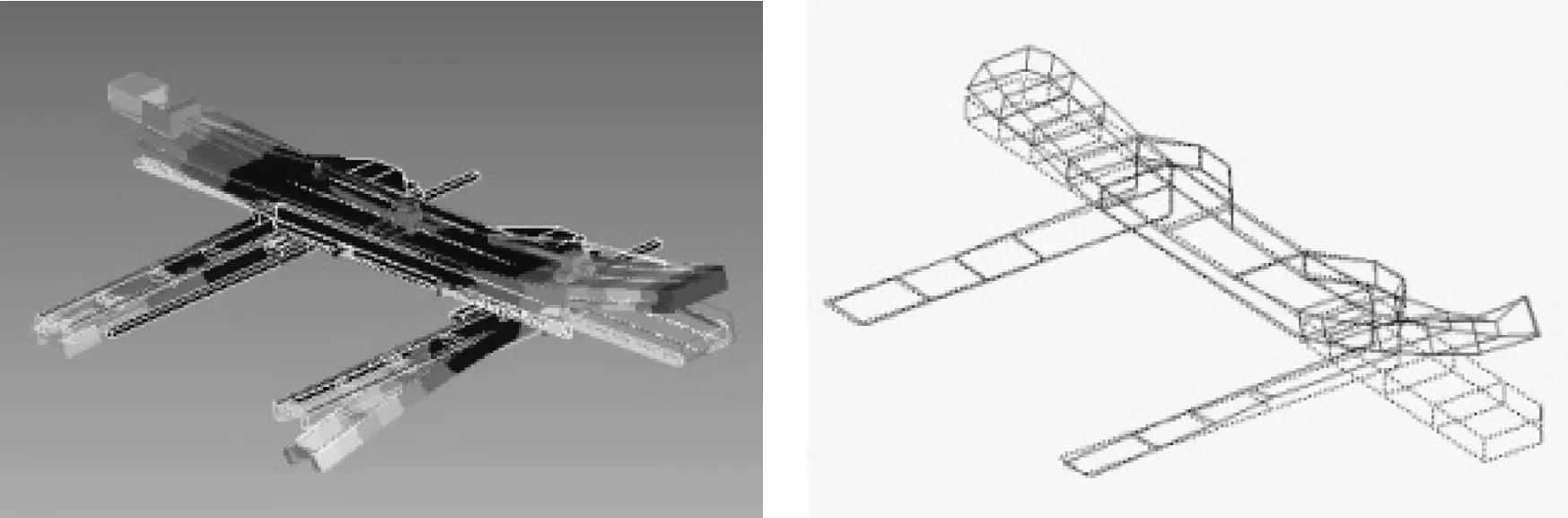
采用Hypermesh软件对零部件划分网格,并建立相应的连接关系,有限元模型如图3所示,网格总数为274 042,计算X轴溜板位于中间时横梁的约束模态;模态实验采用单点激励多点响应的方法(选取横梁端部一点为激励点,横梁结构框架上均匀布置多个响应点),锤击激励频率范围为0～1 000 Hz．将横梁模态测试结果与有限元计算结果进行对比后,得到固有频率最大误差为6.8%,这个误差在允许范围内．有限元计算的前4阶振型和实验模态的前4阶振型如图4所示(模态实验的第2阶振型未激励出来).由图可见，第1阶振型表现为横梁两端上下振动,相位相差180°;第3阶振型表现为横梁基本不动,底下支架上下振动;第4阶振型表现为横梁两端上下振动,且相位一致．通过上述分析可以看出，实验模态振型与有限元计算模态振型相一致,因此验证了本文所建有限元模型的正确性．

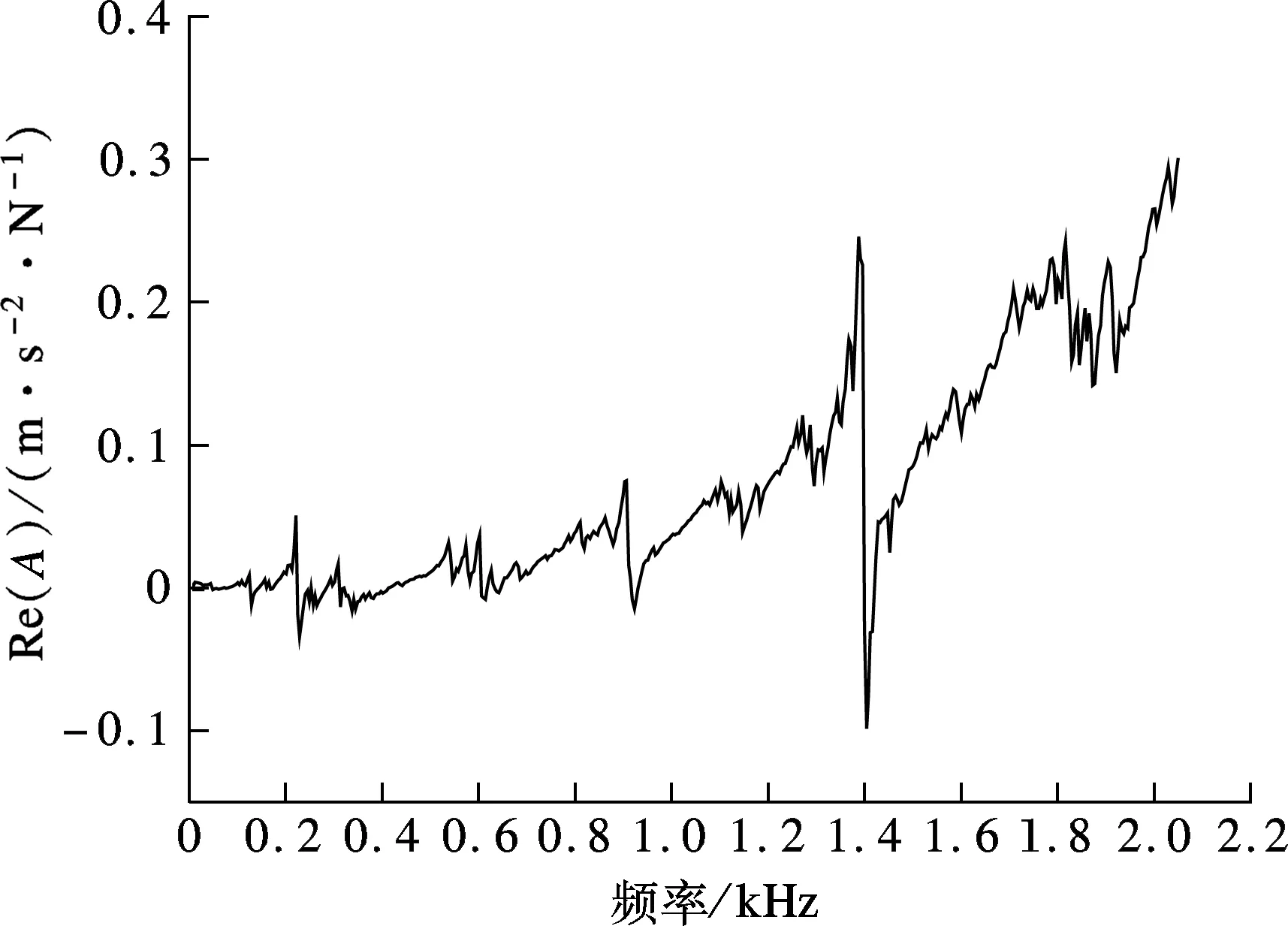
(a) Y方向导轨实频特性曲线

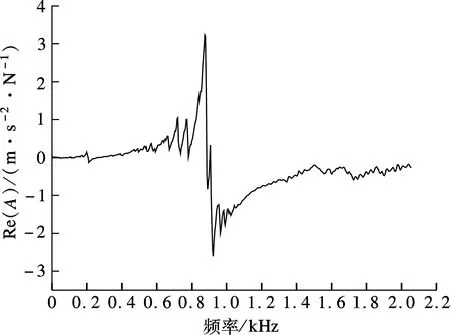
(b) X方向导轨实频特性曲线

(c) Y方向导轨虚频特性曲线

(d) X方向导轨虚频特性曲线

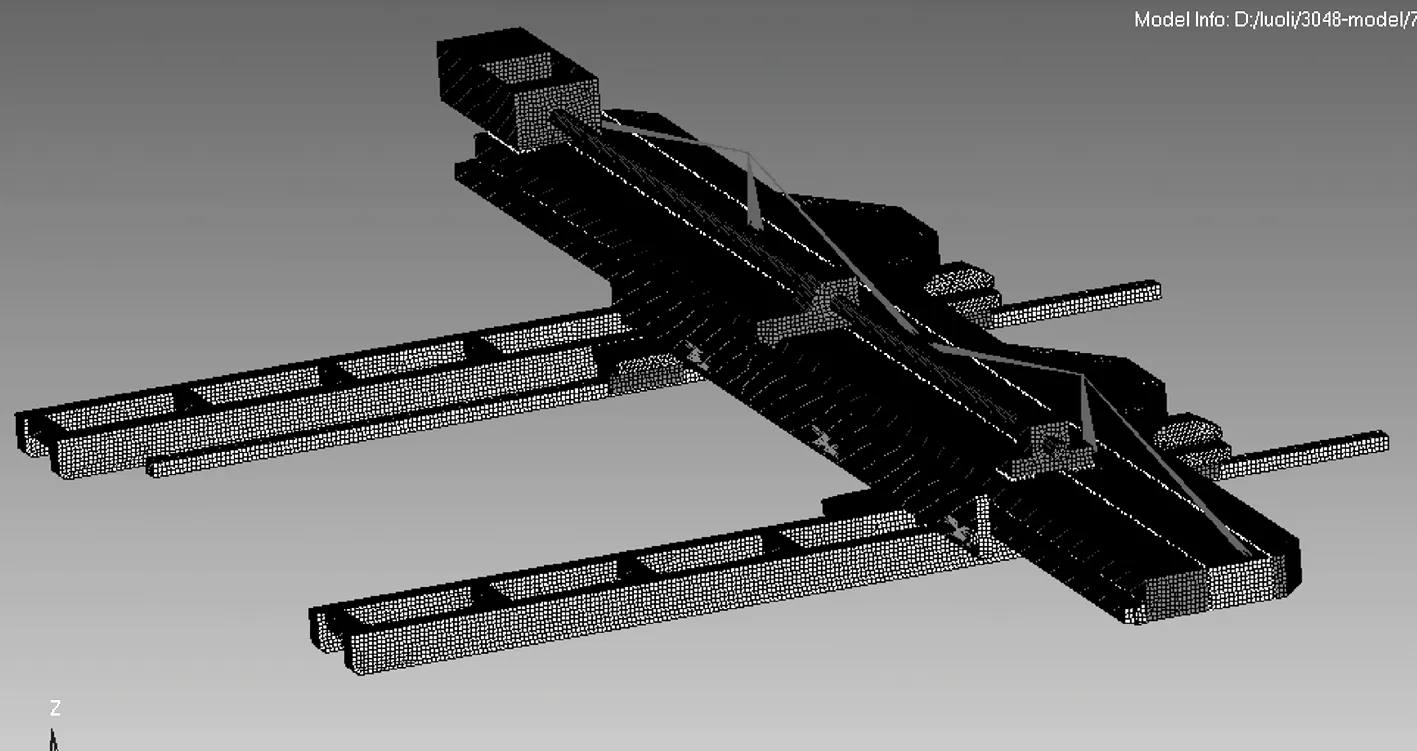
图3 横梁有限元模型

(a) 第1阶，有限元 (b) 第1阶，实验

(c) 第3阶，有限元 (d) 第3阶，实验

(e) 第4阶，有限元 (f) 第4阶，实验

1.5 横梁危险工况静动态性能分析

表3 横梁模态测试与有限元计算结果对比

由于X轴溜板在左右运动过程中,对横梁的动态性能影响较大,尤其是在2个极限位置(最左边与最右边)的情况下,横梁的动态性能较差,加工精度较低．本文对3种工况(X轴溜板在最左边、中间、最右边)进行了计算,结果如表4所示.结果表明:X轴溜板在最左边时一阶固有频率及沿Y方向静刚度最低,变形量最大,因此,本文选取X轴溜板在最左边位置时进行后续的优化计算．其性能参数如下:第1阶固有频率为21.3 Hz;横梁加速度为1.2g时的最大变形为0.999 mm;横梁端部施加2 kN力时,横梁沿Y方向最大变形量为0.107 mm(由于Y方向刚度对加工精度影响较大),横梁Y方向静刚度为

(2)

式中,F为横梁端部施加的力;S为横梁沿Y方向最大变形量．

表4 3种工况下横梁性能参数

2 横梁轻量化设计

通过对横梁进行静动态分析,得到了横梁在最危险工况下的性能参数．本文在保证横梁一阶固有频率、最大变形量、Y方向静刚度基本不变的前提下,对横梁进行轻量化设计,优化流程如图5所示．

2.1 基于网格变形技术的模型参数化

本文将结构壁厚与结构形状作为设计变量,结构壁厚属于尺寸变量的范畴,较容易实现;结构形状属于形状变量,实现难度较大,在结构优化中应用较少[5-6].由于变量的参数化不易实现,形状优化被视为是一个更具挑战性的任务,网格变形技术的出现为形状优化提供了有效的工具．

CAE模型的网格变形通过给定的表述形式实现节点的移动,表述形式可以是矩阵表示的数学形式,也可以是由目标形状定义的几何形式[7-8]．Hypermorph中网格变形过程主要通过可变形区域、变形控制节点和变形约束来实现．变形控制节点有多种变换方式,如平移、旋转、比例缩放和投影等,变形约束是通过控制各节点之间的坐标变化量来控制网格变形后模型的外形．变形过程中,只有网格节点坐标发生改变,而网格编号及网格节点间的拓扑关系不变,因此变形后网格不需要重新划分．

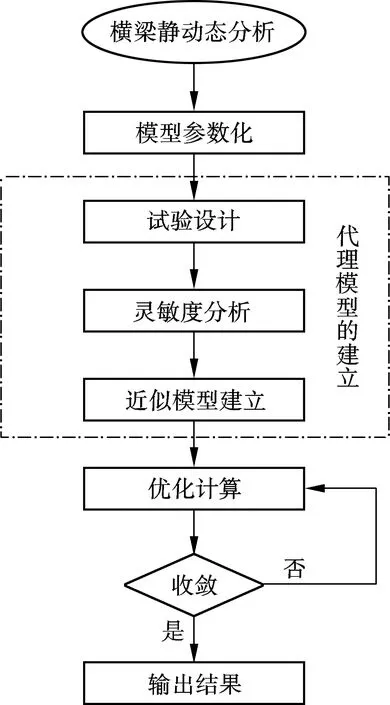
图5 优化流程图

本文建立了4个尺寸变量(变量1～变量4),采用上述方法创建了20个形状变量(变量5～变量24)．根据每个零件的作用、成形特点、市场上的板材规格等因素确定设计变量的范围,如表5所示．结构设计变量示意图如图6所示.

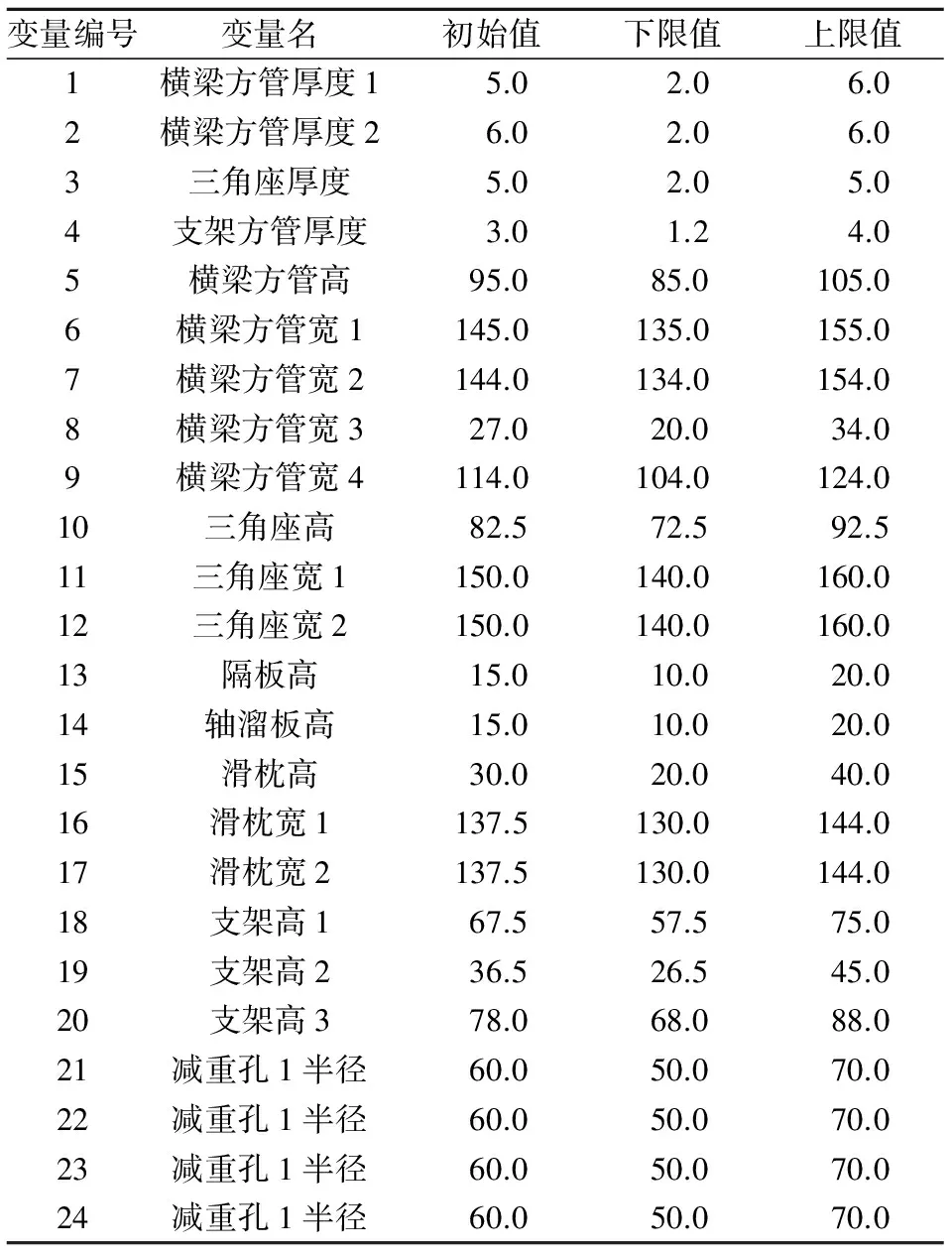
表5 横梁参数化设计变量 mm

2.2 横梁结构优化数值代理模型的建立

本文基于拉丁超立方采样、相对灵敏度分析和Kriging近似模型,建立数值代理模型,可以高效地实现优化迭代,不仅解决了优化有限元网格时产生的穿透和单元质量问题,而且避免了传统优化迭代中需要消耗大量计算成本的有限元仿真分析．该代理模型的建立有如下3个步骤:① 运用拉丁超立方进行试验设计;② 对设计变量进行相对灵敏度分析,筛选设计变量;③ 建立基于Kriging近似模型的优化代理模型．

拉丁超立方采样技术(LHS)是一种常用的研究多因素多水平的试验设计方法．拉丁超立方采样采用多维分层抽样方法,对于k个试验因素的设计问题,LHS的主要步骤为:① 将每个试验因素的设计空间按照概率相等的原则划分为n个互不重叠的分区,每个分区的概率为1/n;② 从设计因素的每一个分区中抽取一个样本,对于k个试验因素,则有n×k个样本;③ 将抽取到的样本进行随机但不重复地配对,最终形成具有n个样本点的设计矩阵,即

Xm=[Xm1,Xm2,…,Xmk]m=1,2,…,n

(3)

灵敏度分析可筛选掉对横梁模态频率、最大变形、静刚度性能敏感的设计变量[9]．一般来说，灵敏度小的零件质量也较小,即最大幅度地减小其结构尺寸,横梁质量也难以有较大的降低.相反,灵敏度大的零件质量也较大,但减轻这些零件的质量会使横梁各项性能参数下降较大,所以在进行绝对灵敏度分析时,可能会将质量大、可减质量的零部件忽略．因此，本文采用相对灵敏度(即质量灵敏度与模态或刚度灵敏度的比值)来进行灵敏度分析．图7为模态相对灵敏度分析结果.由图可见，相对灵敏度数值越大,说明该设计变量对横梁轻量化优化越重要,是需要保留的设计变量．经分析和筛选，发现模态、静刚度、最大变形相对灵敏度值均排在后15位的设计变量(即共有8个设计变量)需筛掉．

近似模型的基本思想是通过数理统计和试验设计的方法,在设计变量和相应值之间建立一种现实的函数关系来近似复杂的实际问题或函数．常用的近似模型方法有最小二乘法(LSR)、移动最小二乘法(MLSM)、Kriging近似模型等, 其中Kriging近似模型在考虑精度和鲁棒性时相对于其他近似模型是相对可靠的[10],故本文采用Kriging近似模型来建立横梁的近似模型．

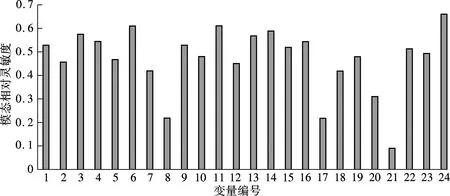
图7 设计变量模态相对灵敏度

Kriging模型是一种基于统计理论,充分考虑变量空间相关特征的差值技术．模型中包含了线性回归部分和随机过程部分，即

y(X)=FT(X)β+Z(X)

(4a)

式中,F(X)为已知的回归模型的基函数,提供模拟的全局近似;β为基函数的回归系数;Z(X)为一个过程,具有以下性质:

E[Z(X)]=0

(4b)

E[Z(W),Z(X)]=δz2[R(θ,W,X)]

(4c)

式中,δz2为该随机过程方差;R(θ,W,X)为点W和点X之间的变异函数;θ为关联模型的参数,表示试验样本之间的空间相关性．

为了提高近似模型的精度,采用试验样本响应值的线性组合来估计任意待测点的响应值,并使其响应值与预测值之间的均方差最小．采用Hyperwork软件近似(approximation)模块来构造Kriging代理模型,并通过残差分析(即求解器提取的响应值和由近似模型提取的响应值之间的差异)来检验近似模型的准确性.图8为体积响应残差图,由图可见，响应点均匀落在直线两侧,因而可以确定所建立的近似模型精度较高．

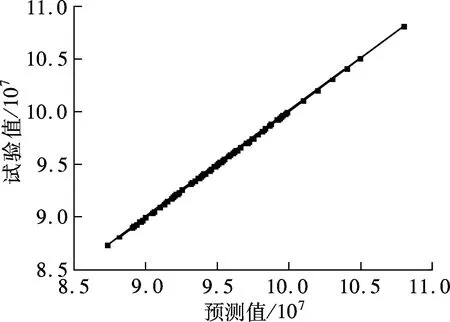
图8 体积响应残差图

2.3 基于遗传算法的轻量化设计

遗传算法是模拟自然界中生物的遗传和变异过程而形成的一种自适应全局优化概率搜索算法,具有良好的全局优化性能和稳健性,且对搜索空间和目标函数没有特殊要求．因此本文采用遗传算法进行优化计算．

本文将横梁体积作为优化目标,横梁一阶固有频率、最大变形以及静刚度作为约束条件,并在上述代理模型的基础上,运用遗传算法进行优化计算,优化结果与原模型对比如表6所示.由表可见,优化后横梁质量减少了5.9%,而一阶固有频率变化了0.4%，最大变形变化了1.0%，横梁静刚度降低了1.8%,总体来说，各约束条件变化较小,仍然满足设计要求．横梁总质量减少了58 kg,轻量化效果较明显．

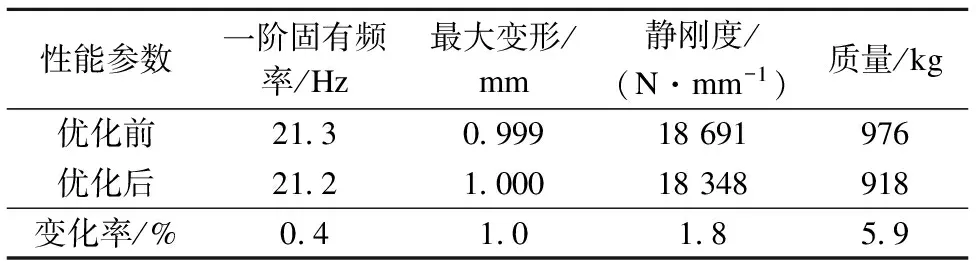
表6 优化前后性能参数对比

为了检验代理模型的正确性,将优化后的尺寸重新导入到有限元中进行计算,计算结果如表7所示.由表可见，代理模型与有限元计算结果之间的误差在2%以内,更进一步说明了所建立的代理模型的准确性．

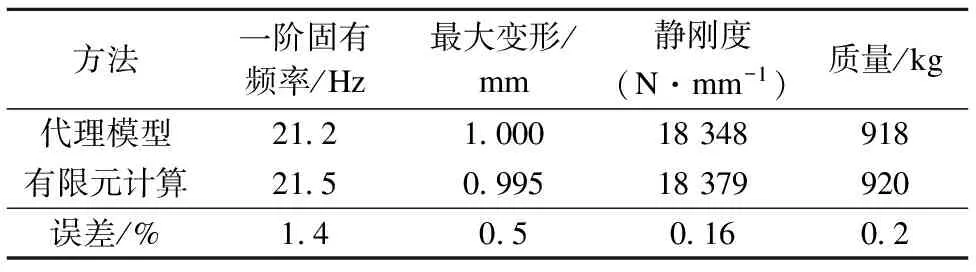
表7 代理模型与有限元计算结果对比

3 结论

1) 针对数控转塔冲床横梁结构的特点,建立了包含导轨结合面的有限元模型,并通过实验验证了有限元模型的正确性,为后续优化设计奠定了基础．

2) 针对现有结构轻量化优化设计大多采用单一变量(如结构壁厚为设计变量)的不足,将网格变形技术应用到横梁结构的轻量化优化中,建立了以结构壁厚和结构形状同时作为变量的参数化有限元模型．

3) 运用拉丁超立方技术对设计空间进行了采样,并采用相对灵敏度分析方法筛选设计变量,结合具有高精度、鲁棒性较好的Kriging模型,拟合得到了用于横梁结构优化的代理模型,高效地实现了优化迭代,避免了传统优化迭代中需要消耗大量计算成本的有限元仿真分析．

4) 结合网格变形技术、代理模型技术和遗传算法,对数控转塔冲床横梁结构进行轻量化设计,在保持横梁性能参数基本不变的情况下,质量减少了58 kg,减重为5.9%．

References)

[1]Kroll L, Blau P, Wabner M. Lightweight components for energy-efficient machine tools [J].CIRPJournalofManufacturingScienceandTechnology, 2011, 4(2):148-160.

[2]Sakundarini C, Taha Z, Abdul-Rashid S H, et all. Optimal multi-material selection for lightweight design of automotive body assembly incorporating recyclability [J].Materials&Design, 2013, 50:846-857.

[3]穆雪峰,姚卫星,余雄庆.多学科设计优化中常用代理模型的研究[J].计算力学学报,2005,22(5):608-612. Mu Xuefeng,Yao Weixing,Yu Xiongqing. A survey of surrogate models used in MDO[J].ChineseJournalofComputationalMechanics, 2005, 22(5):608-612.(in Chinese)

[4]Zhang G P,Huang Y M, Shi W H, et al.Predicting dynamic behaviours of a whole machine tool structure based on computer-aided engineering[J].InternationalJournalofMachineTools&Manufacture, 2003, 43(7): 699-760.

[5]方剑亮,高云凯,王婧人,等. 基于网格变形技术的白车身多目标形状优化[J].机械工程学报,2012,48(24):119-126. Fang Jianliang, Gao Yunkai, Wang Jingren, et al. Multi-objective shape optimization of body-in-white based on mesh morphing technology [J].JournalofMechanicalEngineering, 2012, 48(24):119-126. (in Chinese)

[6]Hae Chang Gea. Topology optimization: a new microstructure based design domain method [J].Computers&Structures, 1996, 61(5): 781-788.

[7]Auweraer H, Langenhove T, Brughmans M, et al. Application of mesh morphing technology in the concept phase of vehicle development [J].InternationalJournalofVehicleDesign, 2007, 43(1/2/3/4):281-305.

[8]季枫,王登峰,陈书明,等.轿车白车身隐式全参数化建模与多目标轻量化优化[J].汽车工程,2014,36(2):254-258. Ji Feng, Wang Dengfeng, Chen Shuming, et al. Implicit parameterization modeling and multi-objective lightweight optimization for a car’s body-in-white [J].AutomotiveEngineering, 2014, 36(2):254-258. (in Chinese)

[9]郭磊,张辉,叶佩青，等.基于灵敏度分析的机床轻量化设计[J].清华大学学报：自然科学版,2011,55(6):846-850. Guo Lei, Zhang Hui, Ye Peiqing, et al. Lightweight design of a machine tool based on sensitivity analysis[J].JTsinghuaUniversity:Science&Technology, 2011, 55(6):846-850. (in Chinese)

[10]Jin R, Chen W, Simpson T W. Comparative studies of meta modeling techniques under multiple modeling criteria[J].JournalofStructuralandMultidisciplinaryOptimaization, 2001, 23(1):1-13.

Parametric modeling and lightweight optimization for cross beam of punch based on grid deformation and agent model

Luo Li Sun Beibei Chen Hanxiang

(School of Mechanical Engineering, Southeast University, Nanjing 211189, China)

The finite element model for cross beam including guide joint surface is established, and the reliability of the model is validated through modal experiments. The static and dynamic analyses for the cross beam under different operating conditions are carried out. Due to the shortcomings of existing optimization methods, a new method is proposed. A parameterized model is set up through the mesh deformation technology. An agent model is built through Latin hypercube sampling, relative sensitivity analysis and the Kriging approximation model. Taking the volume as the goal, the stiffness, strength and the first order natural frequency as the constraint conditions, the lightweight design is produced by GA(genetic algorithms). The optimization results show that the mass of the cross beam can be reduced by 58 kg(5.9%), while the maximum deformation, strength and the first order natural frequency keep basically unchanged.

parameterization; mesh deformation technology; lightweight; agent model

2014-07-29. 作者简介: 罗黎(1990—)，女，硕士生；孙蓓蓓(联系人)，女，博士，教授，博士生导师，bbsun@seu.edu.cn.

江苏省科技支撑计划资助项目(BE2014133)、江苏省前瞻性联合研究资助项目(BY2014127-01)、教育部重点实验室开放基金资助项目(UASP1301).

罗黎,孙蓓蓓,陈翰翔.基于网格变形与代理模型的横梁参数化建模与轻量化优化[J].东南大学学报:自然科学版,2015,45(1):56-62.

10.3969/j.issn.1001-0505.2015.01.011

TG385.1

A

1001-0505(2015)01-0056-07