关于平面解析系统的定性结构

唐 敏, 黄土森

(浙江理工大学理学院, 杭州 310018)

关于平面解析系统的定性结构

唐 敏, 黄土森

(浙江理工大学理学院, 杭州 310018)

首先证明拓扑等价微分系统的两个性质,分析了平面解析系统拓扑结构及其分类的局限性;其次给出平面解析系统定性结构的定义,并根据拓扑结构和定性结构对非退化平面解析系统的奇点进行分类,结果表明平面解析系统的定性结构比拓扑结构能更好地刻画系统的定性行为。这些结果推广了平面解析系统奇点理论中的有关结论,对研究平面解析系统的相图具有参考价值。

相图; 拓扑结构; 定性结构; 分类

0 引 言

微分方程定性理论根据微分方程本身研究其轨道的全局分布情况,因此,在平面微分系统的定性研究中,确定系统的相图的信息十分重要[1]。一个微分系统的相图是指这个微分系统的(定向)轨道的集合[2]。一般地,通过一些有意义的轨道来表示相图,并且对于正则轨道(即不是奇点的轨道),用一个箭头来表示其方向[2]。对于一些特别简单的平面微分系统可以直接画出其相图,但绝大部分平面微分系统却很难直接画出相图,因此,要画出平面微分系统的相图,一般先研究该系统局部相图的结构,画出局部相图,然后构造出整个系统的相图。由于在系统的常点(即非奇点)的轨道的结构是简单的,而在系统的奇点附近的轨道的结构有可能十分复杂[2],因此,在研究平面微分系统的相图时,只需研究系统的奇点附近轨道的结构。正由于系统的奇点附近的轨道的结构可能十分复杂,所以往往对原来的系统在奇点进行某种形式的变换,把奇点分成有本质区别的不同类型,这就是相图的分类问题。目前国内外文献中最常用的相图分类方式是:拓扑等价分类与拓扑共轭分类[3-4]。

本文首先证明拓扑等价微分系统的两个性质,并分析按照拓扑等价分类微分系统是比较粗糙的,因为它不能很好地区分平面解析系统奇点的类型,比如非退化平面线性微分系统的结点与焦点属于同一个拓扑类型,但它们却具有不同的动力学行为。为了能更好地对微分系统进行分类,需引进其他的分类方法。文献[5]研究了非退化平面线性微分系统,认为拓扑结构与定性结构是两个不同的概念,但没有给出定性结构的严格定义。目前国内外的文献还没有给出平面解析系统定性结构的严格定义。如果有轨道进入奇点,那么只能以螺旋形进入或沿固定方向进入。本文将根据平面解析系统的这个特征,给出平面解析系统定性结构的严格定义,并按照拓扑结构和定性结构分别对非退化平面解析系统的奇点进行分类,并进行分析。

1 平面系统的拓扑结构

令

x=f(u,v),y=g(u,v)

(1)

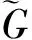
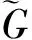
(2)

b)T在G的每个点上是连续的;

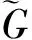
则把T称为uv平面到xy平面的拓扑坐标变换。

定义1.2[4]称T为uv平面到xy平面的正则坐标变换,如果函数组f,g在G的每个点具有直到p≥1的连续偏导数,且满足

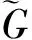
特别地,如果函数组f、g是Cp(或解析)类的,则称相应的正则映射是Ck(或解析)类的。

值得注意的是在平面微分系统的定性研究中,常用的极坐标变换

x=rcosθ,y=rsinθ

在含原点的区域中不是一个拓扑变换。

Andronov等[4]指出一个区域或集合上的平面微分系统的定性性质是指该系统的轨道、轨道的集合以及相图在拓扑映射下保持不变的那些性质,同时用间接的方法定义平面系统的拓扑结构,即不去定义(实际上也难以定义)什么是一个平面微分系统的拓扑结构,而是定义何时两个平面微分系统具有相同的拓扑结构,由此可以对平面微分系统进行分类。

定义1.3[4]给定两个平面微分方程组

(3)

与

(4)

它们分别定义在平面区域G1与G2上。称系统(3)与(4)的相图分别在G1与G2上具有相同的拓扑结构,如果存在G1到G2上的一个映射T,满足下面的三个条件:

a)T是一个拓扑映射;

b) 若G1中的两个点位于系统(3)的同一轨道上,则它们在T下的象位于系统(4)的同一轨道上;

c) 若G2中的两个点位于系统(4)的同一轨道上,则它们在T-1下的象位于系统(3)的同一轨道上。

满足条件a)、b)和c)的一个映射称为从系统(3)到系统(4)的保轨道映射。

把满足定义1.3中的两个微分系统(3)与(4)通常称为是拓扑等价的,并且拓扑映射T一般不能保持时间参数不变。如果T还保持时间参数不变,则称两个微分系统是拓扑共轭的[2-3]。下面给出具有相同拓扑结构的两个微分系统的一个性质。

定理1.4 如果两个微分系统具有相同的拓扑结构,则它们的奇点的个数及闭轨的个数是相同的。

证明:令φ(t,(x,y))与ψ(t,(x,y))分别为系统(3)与(4)生成的流。因为系统(3)与(4)具有相同的拓扑结构,所以存在单调的时间函数α(t,(x,y))使得

T∘φ(t,(x,y))=ψ(α(t,(x,y)),T(x,y)),

其中,T∘φ(t,(x,y))表示T与φ(t,(x,y))的复合[3]。若(x0,y0)是系统(3)的一个奇点,则对任意的t∈R使得φ(t,(x0,y0))=(x0,y0),于是对任意的t∈R使得

T(x0,y0)=ψ(α(t,(x0,y0)),T(x0,y0))。

所以T(x0,y0)是系统(4)的奇点;反之,由于T是一个同胚映射,同理可证:若(x0,y0)是系统(4)的一个奇点,则T-1(x0,y0)是系统(3)的奇点。故系统(3)与(4)的奇点的个数是相同的。其次,如果φ(t,(x0,y0))是系统(3)的一条闭轨道,即存在一个实数τ>0使得

φ(τ,(x0,y0))=(x0,y0)。

从而

T∘φ(τ,(x0,y0))=T(x0,y0)。

于是

ψ(α(τ,(x0,y0)),T(x0,y0))=

ψ(α(0,(x0,y0)),T(x0,y0)),

这表明存在t1=α(0,(x0,y0))及t2=α(τ,(x0,y0))使得

ψ(t2,T(x0,y0))=ψ(t1,T(x0,y0)),

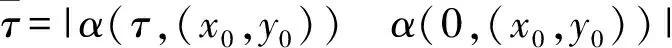
综上,系统(3)与(4)奇点个数及闭轨个数相同。

另外,注意到定义1.3中的拓扑映射T并不要求保持两个系统轨道的方向是一致的,但在文献[2-3]中拓扑等价还要求拓扑映射T保持两个系统轨道的方向也是一致的。可能存在这样的两个系统,保轨道映射能保证区域中的一部分轨道的方向一致,在剩下部分的区域中的轨道的方向是相反的。例如考察下面的两个系统

(5)

(6)

其中G1=G2=R2。取恒等映射为保轨道映射T,则在单位圆外保持轨道的方向一致,而在单位圆内轨道的方向相反,这里单位圆周上的点及原点为奇点。

然而当系统的奇点个数为有限时,可以证明不会出现这种情形。

虽然定义1.3中的两个微分系统的轨道一般都是光滑的(即具有一阶连续的导数,只要两个系统的右端函数是连续的),但不能保证保轨道映射是光滑的。

定理1.5 考虑下面的两个线性系统

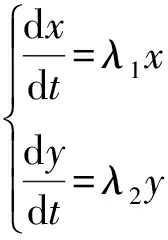
(7)

与

(8)

则它们是拓扑等价的,但保轨道映射T在奇点不可微。

证明:因为t=0时,式(7)过(x0,y0)的解为

热浸镀是一种用途极广的金属材料表面改性技术。它可显著提高金属材料表面的耐蚀性，提高耐高温气蚀，抗氧化或者耐磨性,还可使金属制品表面均匀光洁，具有良好的装饰作用[1]。关于热浸镀铝,德国人在 1893年发表了论文，随后人们相继发明了多种钢材热浸镀铝工艺。1939年，美国阿姆科钢铁公司首先采用森吉米尔法实现了带钢连续热镀铝硅合金的工业化生产。1952年，美国通用汽车公司又实现了熔融熔剂法热浸镀铝的工业化生产，到 60年代，热浸铝钢材的生产与应用几乎遍及所有工业发达的国家。由于镀铝钢材可应用于含硫和含氯的气氛中，可代替某些不锈钢，因此，近年来热浸镀铝钢材的应用日益广泛[2]。

(9)

式(8)过(u0,v0)的解为

(10)

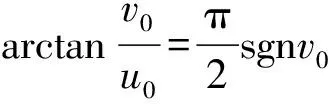
先证明系统(7)与(8)是拓扑等价的。实际上,在xy平面与uv平面中分别取单位圆周

Cxy={(x,y)|x2+y2=1}与Cuv={(u,v)|

u2+v2=1}。

任取(x0,y0)∈Cxy,令(u0,v0)=(x0,y0),并构造xy平面到uv平面的映射T如下:

a)T(0,0)=(0,0);

b) 当x0y0≠0时,(u,v)=T(x,y),其中

c) 当x0y0=0时,可同理定义(u,v)=T(x,y)。

则可以证明映射T是一个系统(7)到(8)的识别映射,因此,系统(7)与系统(8)是拓扑等价的。

再证系统(7)到系统(8)的任何保轨道映射都不是C1。实际上,由于(7)的两个特征值分别为λ1与λ2,而(8)的两个特征值分别为α±iβ,显然它们不对应成比例,故系统(7)与(8)的任何保轨道映射在奇点是不可能可微的。

由定理1.5可知:两个微分系统虽然可以具有相同的拓扑结构,但它们之间的任何保轨道映射可以不具有可微性。

在微分系统的局部定性研究中,只需要考虑局部拓扑结构。令P0是平面微分系统

(11)

定义域G的一个内点,P0可以是一个奇点,也可以是一个常点。

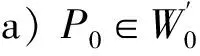
这样的一个区域W0称为系统(9)的局部拓扑结构区域(或邻域)。

由平行化定理可知,在常点的局部拓扑结构是简单的,即从拓扑上讲就是平行线。至于在奇点,其局部拓扑结构可能是十分复杂的,有的系统甚至在上述意义下可能没有局部拓扑结构。

例1.7 考虑下面的平面系统

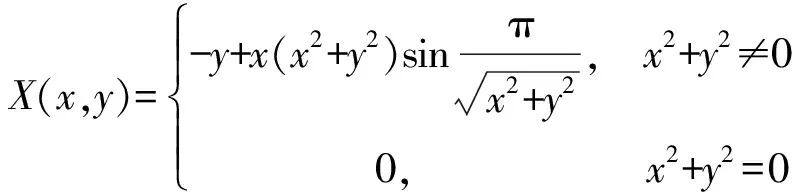
C1:x2+y2=32,C2:x2+y2=22,

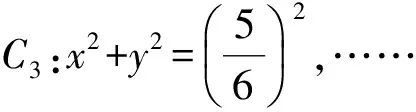
使得在C2k-1与C2k之间没有极限环,而在C2k与C2k+1之间恰有k个极限环。则这个系统在定义1.6意义下奇点O是不具有局部拓扑结构。

然而,对于解析系统而言的任何奇点总是具有局部拓扑结构的,但是难以用直接的方法来定义一个奇点的局部拓扑结构的具体含义,而一般用下面的间接的方法来定义。由于是局部的,这里的保轨道映射不一定映整轨道到整轨道,而是允许映轨道段到轨道段。

定义1.8 令P1与P2分别是系统(3)与(4)的具有局部拓扑结构的两个点(可以是奇点,也可以使正则点)。称系统(3)与(4)在这两个点的局部拓扑结构是相同的,如果分别存在P1与P2的邻域W1与W2及映射

T:W1→W2

使得T(P1)=P2且轨道弧对应于轨道弧段。

2 平面解析系统的定性结构

正如前面的定理1.5所表达的,对于非退化平面线性微分系统的焦点与结点,它们的拓扑结构是相同的,然而从动力学上看,它们显然有本质的区别。因此在有些文献,比如文献[5]中,认为平面微分系统的拓扑结构与定性结构是不同的。正如定义1.3或定义1.6那样,两个平面微分系统的拓扑结构是否相同可以通过一个拓扑映射来定义。至于如何定义两个平面微分系统的定性结构是否相同,就作者所知,目前国内外文献还没有严格的定义,大多数文献中就某两个具体的微分系统讨论它们是否具有相同的定性结构,比如对非退化平面线性微分系统,焦点、结点(包括正常结点、退化结点与临界结点)具有相同的拓扑结构,但它们具有不同的定性结构[5]。

下面对平面解析系统,利用文献[2,5]中的一个结果给出其定性结构的严格定义。

命题2.1[2,5]若原点O(0,0)是式(7)的奇点,即X(0,0)=Y(0,0)=0,且设X(x,y),Y(x,y)在原点的一个邻域U中是解析的。则式(11)如果有轨道进入奇点O(0,0),它只能螺旋形地进入或沿固定方向进入。

定义2.2 定两个平面解析系统

(12)

与

(13)

设P1与P2分别是式(12)与(13)的孤立奇点,且在它们的邻域中有定义。称系统(12)与(13)在P1与P2具有相同的定性结构,如果满足下面两个条件:

a) 它们在定义1.6意义下具有相同的拓扑结构,记保轨道段映射为T;

b) 系统(12)的一条轨道段沿固定方向趋于P1当且仅当在映射T下对应于系统(13)的轨道段沿固定方向趋于P2;等价地,系统(12)的一条轨道段螺旋形地趋于P1当且仅当在映射T下对应于系统(13)的轨道段螺旋形地趋于P2。

命题2.1表明,上面的定义是合理的。有了定性结构的严格定义以后,类似于根据拓扑结构对平面系统进行拓扑分类,现在可以利用定性结构,也可以对平面解析系统进行分类。

考虑平面非退化的解析系统

(14)

其中a、b、c、d是实数,且ad-bc≠0,而Φ(0,0)=ψ(0,0)=0。显然原点O(0,0)是孤立奇点,并且

是系统(14)的特征方程。若令p=-(a+d),q=ad-bc,则D(λ)=λ2+pλ+q=0,该方程的根

称作系统(14)的特征根。

由于对任何n阶常系数线性系统,当特征根实部k个为负,n-k个为正(k=0,1,…,n),对固定的k,它们的轨道的拓扑结构都相同[5],因此当按拓扑结构对系统(14)的奇点进行分类时,只有以下三种不同的类型:

a) 若λ1、λ2的实部同号,则系统(14)的焦点或结点为一类;

b) 若λ1、λ2的实部异号,则(14)的鞍点为一类;

c) 若λ1、λ2的实部均为零,则(14)的中心为一类。

由a)可知,当按拓扑结构来分类系统(14)时,不能把系统的焦点与结点区分开来。然而,从动力学的角度来看,焦点与结点是不同的,因此按照拓扑结构来分类系统(14)是比较粗糙的。现按定义2.2的定性结构对系统(14)的奇点进行分类,则它的奇点可分为下面六种不同的类型:

a) 若λ1,λ2为两个不同的实根且同号,则存在两条不同的直线,使得系统(14)的奇点附近的所有轨道都沿确定的方向进入(或离开)奇点,并且只有两条轨道沿两条直线中的一条所确定的方向相向进入(或离开)奇点,剩下的所有轨道沿另外一条直线所确定的方向进入(或离开)奇点,称这样的奇点为正常结点;

b) 若λ1,λ2为两个相同的实根,且初等因子为单时,则对过奇点的任意直线,有且仅有系统(14)的奇点附近的两条轨道沿这条直线所确定的方向相向进入(或离开)奇点,称这样的奇点为临界结点;

c) 若λ1,λ2为两个相同的实根,且初等因子为重时,则存在一条直线,使得系统(14)的奇点附近的所有轨道只可能沿这条直线所确定的方向进入(或离开)奇点,称这样的奇点为退化结点;

d) 若λ1,λ2为两个异号的实根,则存在过奇点的两条直线与系统(14)的奇点附近的四条轨道,使得其中的两条轨道沿其中的一条直线所确定的方向相向进入(或离开)奇点,而另外两条轨道沿另一条直线所确定的方向相向离开(或进入)奇点,称这样的奇点为鞍点;

e) 若λ1,λ2为两个共轭的复特征根,且实部非零,则系统(14)的奇点附近的所有轨道只能螺旋形地进入(或离开)奇点,称这样的奇点为焦点;

f) 若λ1,λ2为两个共轭的纯虚根,则系统(14)的奇点附近的所有轨道或者都是闭的,或者所有轨道只能螺旋形地进入(或离开)奇点,出现前者称为中心,出现后者称为细焦点。关于中心与细焦点的区分问题称为稳定性问题,虽然理论上已经解决,但对一个具体的系统要区分它们仍有待继续研究的课题。

通过上面的分析可知,虽然焦点、正常结点、退化结点、临界结点具有相同的拓扑结构,但它们却具有不同的定性结构,并且轨道的动力学行为存在很大的差别。所以按定性结构对平面非退化的解析系统的奇点进行分类比拓扑结构进行分类更加精细,从而能够更好地刻画系统的动力学行为。至于一般的平面解析系统的奇点(特别是退化奇点)的定性结构分类问题仍有待继续研究,但下面的结果表明这样的类型只有有限多个。

命题2.3[2,5]设O(0,0)是系统(11)的具有局部拓扑结构的孤立奇点,则存在O(0,0)的一个邻域Sδ(O),使得在Sδ(O)的闭包内的双曲扇形与抛物扇形的个数是有限的,从而椭圆扇形的个数也是有限的。

定理2.4 设O(0,0)是系统(11)的具有局部拓扑结构的孤立奇点,则奇点O(0,0)仅有有限种不同类型的定性结构。

证明 由定义1.6与命题2.4立即得到。

3 结 论

微分方程定性理论的基本思想是根据微分系统本身的结构与特点,用尽可能简单的方法来确定其轨线的分布图形,即对微分系统的轨线作“全局”分布的研究。这必须解决三个问题:奇点附近轨线的结构、经过奇点的分界线的去向、极限环的个数及相对位置。为研究奇点附近轨线的结构,通常用拓扑变换法对系统的奇点进行拓扑分类,使得属于同一类的奇点具有相同的拓扑结构。但正如本文中所分析的那样,虽然拓扑等价系统具有相同个数的奇点与极限环(见定理1.4),但由于这样的拓扑变换可能是不可微的(见定理1.5),所以在使用上是不方便的;同时平面非退化线性系统的焦点与结点属于同一个拓扑类型,因此在这个意义下对奇点进行拓扑分类是比较粗糙的,它不能很好地区分系统奇点的动力学行为。为了能更好地对微分系统的奇点进行分类,本文根据平面解析系统如果有轨道进入奇点只能螺旋形地进入或沿固定方向进入这个特征给出了平面解析系统定性结构的定义,并按照拓扑结构和定性结构分别对平面非退化解析系统的奇点进行分类,结果是:按照拓扑结构可以分为三类,其中焦点与结点属于同一类;按照定性结构可以分为六类,把焦点、正常结点、退化结点与临界结点区分开来。这表明,对于平面非退化解析系统,按定性结构进行分类比按照拓扑结构进行分类能更好地刻画系统的动力学行为。至于一般的平面解析系统的奇点(特别是退化奇点)的定性结构分类问题仍有待继续研究。

[1] Algaba A, Fuentes N, García C. Centers of quasi-homogeneous polynomial planar systems[J]. Nonlinear Analysis: Real World Applications, 2012, 13: 419-431.

[2] Dumortier F, Llibre J, Artes J C. Qualitative Theory of Planar Differential Systems[M]. Berlin: Springer-Verlag, 2006: 4-8.

[3] Wiggins S. Introduction to Applied Nonlinear Dynamical Systems and Chaos[M]. New York: Springer-Verlag, 1990: 1-6.

[4] Andronov A A, Leontovich E A, Gordon I I, et al. Qualitative Theory of Second-order Dynamic Systems[M]. Israel Program for Scientific Translations. New York: Halsted Press(A Division of Wiley), 1973: 6-12.

[5] 张芷芬, 丁同仁, 黄文灶, 等. 微分方程定性理论[M]. 北京: 科学出版社, 1985: 19-96.

(责任编辑： 康 锋)

Analysis on Qualitative Framework of Planar Analysis System

TANGMin,HUANGTu-sen

(School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018, China)

This paper firstly proves 2 properties of topological equivalence differential systems, and analyzes topological structure of planar analytic system and limitations of its classification; and then gives the definition of qualitative framework of planar analytic system, and makes classification according to the singular points of topological structure and qualitative framework on non-degenerating planar analytic system. The result shows that the qualitative framework of planar analytic system can better depict qualitative behavior of system compared with topological structure. Those results popularize relevant conclusions in singular point theory of planar analytic system, and have reference value to research on phase diagram of planar analytic system.

phase diagram; topological structure; qualitative framework; classification

1673- 3851 (2015) 01- 0140- 06

2014-03-10

国家自然科学基金项目(10871181,11101370)

唐 敏(1990-),女,贵州普安人,硕士研究生,主要从事微分方程定性理论方面的研究。

O175.14

A