时间偏移下的多源目标精确定位方法

2015-05-06严长虹

传感技术学报 2015年2期

关键词：信标偏移量测距

严长虹,金琳

(1.盐城工学院信息学院,江苏盐城 22400;2.盐城工学院经济与管理学院,江苏盐城 22400)

时间偏移下的多源目标精确定位方法

严长虹1*,金琳2

(1.盐城工学院信息学院,江苏盐城 22400;2.盐城工学院经济与管理学院,江苏盐城 22400)

采用到达时间(TOA)测距实现源目标定位的方法比较简单,因此在无线传感器网络定位领域得到了广泛的应用。将TOA定位模型转化为线性优化问题,提出了一种存在时间偏移下的多源目标精确定位方法。该方法将定位计算过程分成两步,包括多源目标位置初始值估计和优化计算过程。两步计算方法将定位结果用代数解表示,避免了数值计算过程中的局部最优问题。仿真分析了时间偏移量及噪声大小对定位误差的影响。结果表明即使存在较大的时间偏移量,优化计算后的定位误差也能非常接近于克拉美罗(CRLB)下界值。

无线传感器网络;定位;到达时间(TOA);多源目标

节点位置坐标的自主估计是无线传感器网络中的重要内容[1-2],为了满足部署大量无线传感器节点的廉价要求,定位的硬件成本必须较低,因此传统的GPS定位方法对无线传感器网络来说是不适合的。GPS定位方法的局限性激发了一种新的传感器网络定位方法,即利用已知位置的信标节点去推算其余未知源目标节点的位置坐标。在这种定位方式下,定位过程可划分为两步:借助于一定的方法测量或估计节点间的距离或方向角信息;以节点间的这些信息通过定位算法求出源节点坐标。因此,定位精度不但取决于测量技术的精度,而且也决定于所采用的定位算法。

国内外已经开展了很多无线传感器网络定位方法的研究,这些定位方法大多数在定位成本和定位精度间进行权衡选择[3]。通常测距误差越小,定位算法获得的定位精度越高,当然对测距方法的要求也就越高。根据定位过程中是否需要直接测量节点间距离,可以把定位算法分为:基于非测距和测距的定位算法。非测距定位算法无需测量节点的绝对距离或方位,而是利用节点间的链路关系估计距离并计算节点位置,定位成本较低,但定位误差相对较大[4]。为获取较高的定位精度,一般采用测距定位算法。测距定位算法需要直接测量节点间的绝对距离或方向角,并利用节点间的实际距离来计算未知节点的位置,该方法需要测量节点间间距,常用的测量有接收信号强度指示(RSSI)[5-6],到达时间(TOA)[7],到达时间差(TDOA)[8]和声音能量强度[9]等方法。

在已知信号传播速度的前提下,TOA方法根据信号在两个目标之间的传播时间来估计发送者和接收者之间的距离,相比较而言,其实现原理简单,因此已有大量的文献介绍使用该方法实现目标定位[10-14]。Chan等[10]提出了基于一种TOA测距方法下的最优线性无偏估计方法,但该方法没有考虑节点间到达时间偏差。文献[11]以目标间的发射与反射TOA测距模型,提出了一种精确的被动目标位置线性估计方法,但该方法并未考虑节点间的时间偏移量。为此Wang等[12]对存在时间偏移量下的被动目标位置估计进行了改进,并提出了定位计算方法。也有学者将定位优化模型转化为凸优化问题,如文献[13]提出源节点信号发射时间未知下的半正定规划(SDP)放松定位算法,但该文献并未考虑多源定位问题。为此文献[14]介绍采用SDP放松方法将上述TOA定位模型扩展到多源目标定位。SDP定位方法的不依赖于初始解,但计算复杂度较高。

根据节点间的TOA往返时间测距模型并考虑节点间存在传送时间偏移量,本文将多源目标定位问题转化为线性估计模型,以两步线性计算方法精确确定源目标位置坐标,提出了存在时间偏移量下的多源目标精确定位计算方法。本文第1部分首先介绍了多源TOA定位问题描述;第2部分推导了该定位模型下的CRLB下界值;第3部分详细介绍了所设计的定位计算方法,包括目标位置初始值估计及优化计算过程;第4部分为仿真与分析;最后部分为结论。

1 问题描述

考虑在二维平面上分布着M+N个节点,其中包括N个未知位置坐标的源节点(源节点的坐标值假设为xi=[xiyi]T,i=1,2,…,N)以及M个已知位置坐标的信标节点(其坐标值为xj=[xjyj]T,j=N+1,N+2,…,N+M,信标节点位置坐标可以预先部署GPS或依靠人力测量方式获取)。信标节点j发送给源节点i信号,源节点i接收到该信号后立刻又转发回信标节点j,将节点间的信号往返时间记为ti,j,因此有

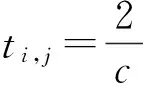
(1)

(2)

显然对式(2)所描述的优化问题可采用数值方法计算。然而当采用数值计算方法时,计算结果依赖于初始值,若初始值选择不合适,可能会使结果陷入局部最优,导致计算结果错误。

为此本文提出一种存在时间偏移下的多源目标位置线性估计方法。该方法采用两步线性估计方法实现,将定位结果采用代数解表示,避免了数值计算方法下选择初始解的问题。首先将非线性优化定位模型转化为线性估计问题,初步估计多源目标节点位置坐标。然后对初步估计的源目标位置进行再次优化求精计算,从而得到目标位置的精确解。

2 克拉美罗下界值

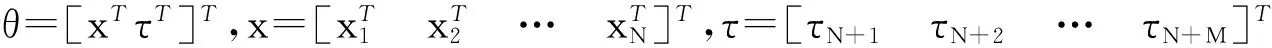
(3)

式(3)中,

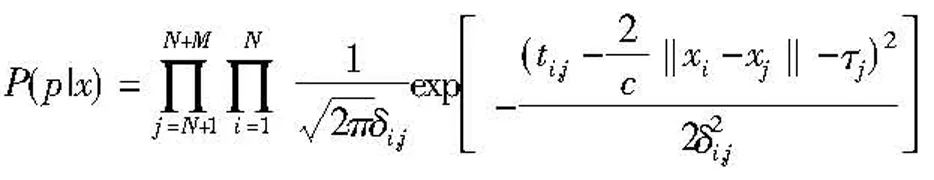
(4)

将式(4)代入式(3)并求微分,因此有F∈R(2N+M)×(2N+M),并且矩阵F的元素值为

(5)

式(5)中,j∈Ai表示了源节点i与信标节点j间可测距。向量θ的CRLB下界为F逆矩阵的对角元素,可以表示为

(6)

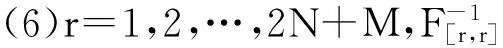
(7)

3 多源目标定位

式(2)所描述的TOA测距模型中包含未知参数τj,故难以实现对单源节点目标位置的确定,本节设计了多源目标的两步线性估计方法,以精确定位目标节点位置坐标。

3.1 多源目标位置初始值估计

将式(1)重新表示为

2‖xi-xj‖=c(ti,j-τj-ni,j)

(8)

式(8)中,i=1,2,…,N,j=N+1,N+2,…,N+M且j∈Ai。对式(8)左右两边平方,忽略高阶项,式(8)再表示为

(9)

由于τj≪tij,将式(9)再次表示为

(10)

Aη=b+α

(11)

式(11)中,α为噪声部分,矩阵A的行向量值为:

当所有源节点与信标节点间共存在L次TOA测距时,A∈RL×(3N+M),b∈RL×1,α∈RL×1。

根据线性最小二乘平方原理,未知参数η的无偏估计值为

(12)

式(12)中维度为L×L的矩阵Σα=E(αTα),其值大小为

(13)

式(13)中,Σα的计算取决于参数值τj。可预先设置Σα为单位矩阵,近似地求解时间偏移值τj,j=N+1,N+2,…,N+M,然后以该近似值计算Σα,再以式(12)重新精确计算参数η。

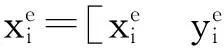
3.2 目标位置优化计算

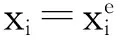
(14)

Δτ=[ΔτN+1ΔτN+2…ΔτN+M]T,可将式(14)写成如下矩阵形式

CΔθ=d+α

(15)

(16)

式(16)中维度为L×L的矩阵Σα=E(αTα),其值计算同式(13)。同样根据参数Δθ的定义,从参数Δθ抽取出Δxi即为优化增量部分。因此最终的源节点目标位置可以表示为

(17)

式(17)中,i=1,2,…,N。

将参数Δθ的方差表示为ΣΔθ,由式(16)可以推导出ΣΔθ有以下关系式

(18)

3.3 算法的计算复杂度分析

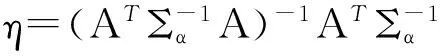
O[2L2(3N+M)+L(3N+M)2+(3N+M)3]≤

O[(3N+M)(2M2N2+3MN2+M2N+(3N+M)2]≈

O(6M2N3+2M3N2)

(19)

O[2L2(2N+M)+L(2N+M)2+(2N+M)3]≤

O[(2N+M)(2M2N2+2MN2+M2N+(2N+M)2]≈

O(4M2N3+2M3N2)

(20)

4 仿真分析

针对上述所设计的两步线性估计方法,采用MATLAB软件进行了仿真与分析。在100m×100m的二维平面上,分别设置5个信标节点(M=5)在(25,25),(25,50),(50,50),(75,25),(75,75)坐标点。同时随机生成了10个源节点(N=10),当源节点与信标节点间距离小于60m时,认为可实现TOA测距,源节点位置坐标及节点间测距情况如图1所示。为评价所设计算法的定位性能,源节点的定位精度采用均方误差(MSE)判断。假设目标节点与源节点间的测距噪声都服从均值为0,方差为δ2的高斯分布,首先仿真测试了不同源节点ID上的定位误差结果。

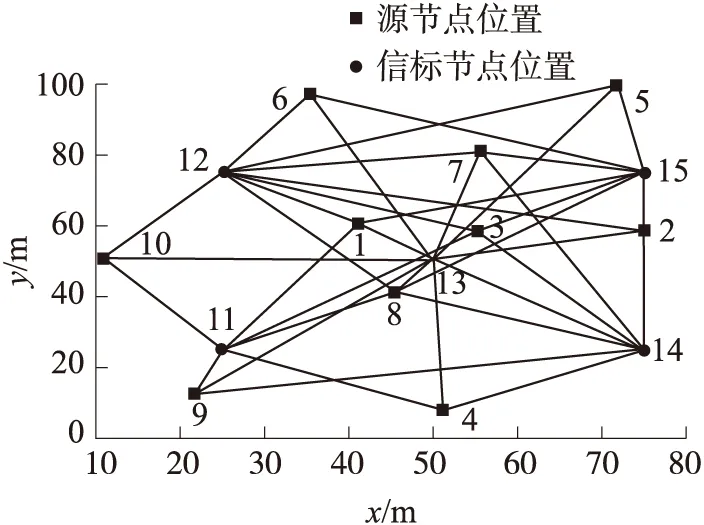
图1 节点地理位置分布

4.1 不同源节点ID的定位误差比较

设置所有源节点和信标节点间的测距噪声为δ2=12,所有信标节点上的时间偏移量τj=τ=20 ns,j=N+1,N+2,…,N+M。对算法下的MSE定位误差仿真运行5 000次,采用5 000次运行结果的平均值分析其定位误差,图2绘出了不同源节点上的定位误差比较结果。由该图可见,经过优化计算后,所有源节点上的定位结果较初始估计值有极大的改善,已基本与CRLB下界值一致。由于所采用的信标节点位置分布不同,经过优化计算后各源节点上的定位误差有所不同,如源节点ID为5的对数MSE值,即10log(MSE)为-11.7 dB,而源节点ID为8的对数MSE值为-15.4 dB。

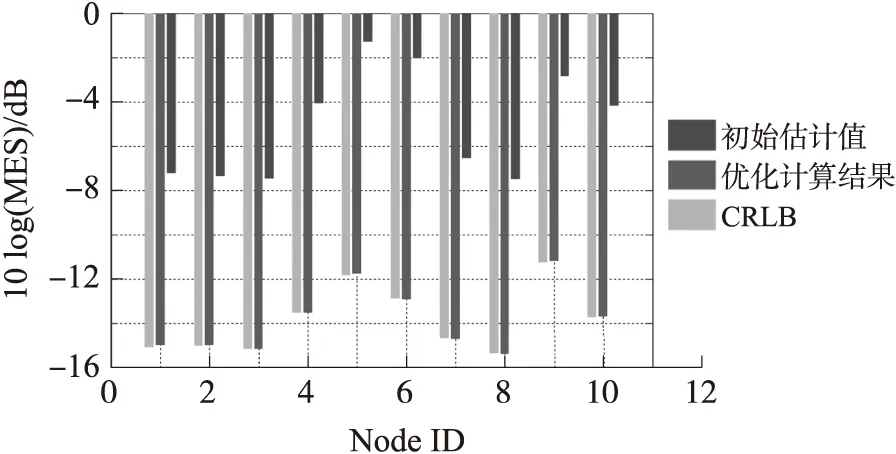
图2 不同源节点ID的定位误差比较

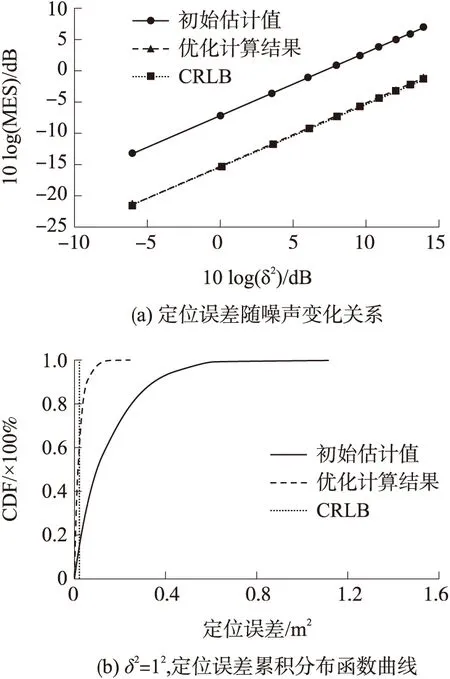
图3 源节点ID为8时噪声对定位误差的影响

4.2 噪声对定位误差的影响

调整噪声δ2从0.52到52之间变化,即10log(δ2)从-6.0dB到14.0dB之间变化,时间偏移量τ=20ns,图3(a)绘出了源节点ID为8时定位误差与噪声之间的变化关系。该图反映的结果同图2结果一致,经过优化计算后的源节点定位结果较初始估计值有极大的改善,非常接近CRLB下界值。同时也可以看出对数MSE值与噪声10log(δ2)之间有近似的线性关系,随着噪声的增加而增大。当噪声10log(δl2)为-6.0dB时,优化计算后的对数MSE值为-21.3dB;而当噪声10log(δ2)为14.0dB时,优化计算后的对数MSE值增加到了-1.2dB。

设定δ2为12,时间偏移量τ=20ns,图3(b)绘出了5 000次随机测试下、源节点ID为8的定位误差的累积分布函数曲线(CDF)。初始估计值下仅有15%左右的定位误差小于CRLB,而经过优化计算后,有65%左右的定位误差小于CRLB下界值,说明经过优化计算后,定位误差大大减少了。

4.3 时间偏移量对定位误差的影响

目标位置初始值估计时,方程对时间偏移量进行了近似线性处理,导致初始估计出现偏差,为此仿真分析了时间偏移量τ对定位误差的影响。设定δ2为12,调整时间偏移量τ从20ns到200ns之间变化,图4绘出了ID为5和8的源节点的定位误差随时间偏移量的变化关系曲线。由该图可见,初始估计值的定位误差随着时间偏移量τ的增加而增大,而经过优化计算后,两个节点的定位误差随时间偏移量τ的增加而保持基本不变。当时间偏移量τ=20ns时,源节点ID为5的初始估计的对数MSE值为-1.1dB,优化计算后的对数MSE为-11.8dB;当时间偏移量τ=200ns时,初始估计的对数MSE值增加到了1.3dB,而优化计算后的对数MSE值仍然为-11.8dB,该结果说明优化计算结果更加可靠。

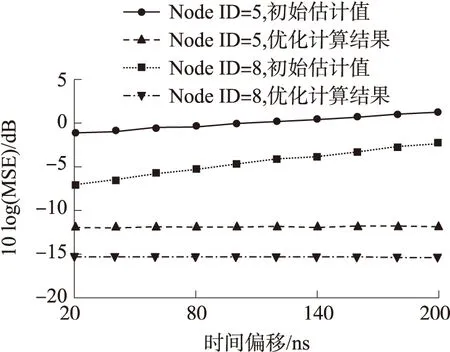
图4 定位误差随时间偏移量的变化关系

5 结论

本文介绍了一种存在时间偏移下的多源目标定位方法。该方法通过目标位置的初始值估计和优化计算两步过程实现,经过优化计算后的定位精度可以基本和CRLB下界值一致。以多源目标定位问题为出发点,将定位问题模型描述为线性最小二乘估计问题,避免了数值计算方法中因初始值选择不当而引起的局部最优问题。仿真结果发现,优化计算后的定位结果具有较高的可靠性,在较大的时间偏移量下,其定位误差还可以保持稳定,非常接近于CRLB下界值。

[1] 叶苗,王宇平.一种新的容忍恶意节点攻击的无线传感器网络安全定位方法[J].计算机学报,2013,36(3):532-544.

[2]Zhao Jizhong,Xi Wei,He Yuan,et al.Localization of Wireless Sensor Networks in the Wild:Pursuit of Ranging Quality[J].IEEE Transactions on Networking,2013,12(1):311-323.

[3]Liu Yunhao,Yang Zheng,Wang Xiaoping,et al.Location,Localization,and Localizability[J].Journal of Computer Science and Technology,2010,25(2):274-297.

[4]Zhong Ziguo,He Tian.Achieving Range-Free Localization Beyond Connectivity[C]//Proceedings of ACM SenSys,2009:281-294.

[5]Robin Wentao Ouyang,Albert Kai-Sun Wong,Chin-Tau Lea.Received Signal Strength-Based Wireless Localization Via Semidefinite Programming:Noncooperative and Cooperative Schemes[J].IEEE Transactions on Vehicular Technology,2010,59(3):1307-1318.

[6]吴晓平,陆炳斌,沈浩.基于RSSI定位模型的非视距关系识别方法[J].传感技术学报,2013,26(11):1584-1589.

[7]Ismail Güvenç,Chong Chiachin.A Survey on TOA Based Wireless Localization and NLOS Mitigation Techniques[J].IEEE Communications Surveys and Tutorials,2009,11(3):107-124.

[8]Yang Le,Ho K C.An Approximately Efficient TDOA Localization Algorithm in Closed-Form for Locating Multiple Disjoint Sources With Erroneous Sensor Positions[J].IEEE Transactions on Signal Processing,2009,57(12):4598-4615.

[9]吕方旭,张金成,刘立阳.基于WSN的多声源目标定位算法[J].传感技术学报,2012,25(8):1121-1125.

[10]Chan F K W,So H C,Zheng J,et al.Best Linear Unbiased Estimator Approach for Time-of-Arrival Based Localisation[J].IET Signal Processing,2008,2(2):156-162.

[11]Shen Junyang,Andreas F Molisch,Jussi Salmi.Accurate Passive Location Estimation Using TOA Measurements[J].IEEE Transactions on Wireless Communications,2012,11(6):2182-2192.

[12]Wang Yuan,Ma Shaodan,Philip Chen C L.TOA-Based Passive Localization in Quasi-Synchronous Networks[J].IEEE Communications Letters,2014,18(4):592-595.

[13]Xu Enyang,Ding Zhi,Dasgupta Soura.Source Localization in Wireless Sensor Networks From Signal Time-of-Arrival Measurements[J].IEEE Transactions on Signal Processing,2011,59(6):2887-2897.

[14]Shen Hong,Ding Zhi,Dasgupta Soura,et al.Multiple Source Localization in Wireless Sensor Networks Based on Time of Arrival Measurement[J].IEEE Transactions on Signal Processing,2014,62(8):1938-1949.

Accurate Positioning Approach of Multiple Source Target Under Time Offest

YANChanghong1*,JINLin2

(1.School of information engineering,Yancheng Institute of Technology,Yancheng Jiangsu 224000,China;2.School of Economics and Managment,Yancheng Institute of Technology,Yancheng Jiangsu 224000,China)

It is relatively simple to utilize time of arrival(TOA)ranging for realizing the positioning of multiple source targets,so it is widely applied in the positioning field of wireless sensor networks.Converting the TOA positioning model to the problem of linear optimization,an accurate positioning method for multiple source targets is put forward when there are time offsets.The method divides the process of positioning calculation into two steps,including the initial estimation of multiple source targets and the process of optimization computation.The two-steps calculation method represents the positioning results as the algebraic solutions and avoids the local optimum problem in the process of numerical calculation.The simulations analyze the impacts of time offsets and noises on the positioning errors.The results show that the positioning errors of the optimization calculation can be very close to the Cramer Rao lower bound(CRLB),even if there are larger time offsets.

wireless sensor networks;localization;time of arrival(TOA);multiple source target