基于可变电阻的超级电容精确建模方法*

2015-05-06索春光刘士华张文斌严玉廷

传感技术学报 2015年2期

关键词：等效电路充放电残差

索春光,刘士华,张文斌,苏适,严玉廷,杨洋

(1.昆明理工大学,昆明 650000;2.云南电力试验研究院(集团)有限公司电力研究院,昆明 650063)

基于可变电阻的超级电容精确建模方法*

索春光1*,刘士华1,张文斌1,苏适2,严玉廷2,杨洋2

(1.昆明理工大学,昆明 650000;2.云南电力试验研究院(集团)有限公司电力研究院,昆明 650063)

超级电容应用越来越广泛,精确的模型可以真实的反映实际应用场合的信息,给用户的使用提供依据。然而传统的模型忽略了等效电路模型中各个参数和充放电电流的关系,所以模型精确度较低。提出将等效电路模型中的一个常电阻扩展为一个随电流变化的可变电阻的模型。通过多种倍率的充放电实验获取建模所需的实验数据,使用Parameter Estimation工具辨识出模型的各个参数值。采用多项式拟合的方法精确可变电阻的动态值。结果表明,无论是在大电流、小电流下,还是大小电流切换的瞬间,扩展的超级电容模型动态特性更加准确。

超级电容;等效电路模型;参数辨识;动态模型

由于超级电容功率密度大,瞬间可以大功率放电,更具有充放电次数多和使用寿命长的特点[1]。所以,超级电容在电能的存储和回收方面具有广泛的应用。超级电容大多应用在混合动力汽车[2-3]、直流电源[4]、城市轨道牵引网路[5]、无线传感网络[6]和微电网[7]等领域。例如,由于无线传感器自身携带的电池能量有限,需要尽可能的收集能量,所以近些年学者把超级电容也应用于传感技术领域[8],其中文献[8-9]将带有超级电容的电源管理电路应用于传感器,延长了电源系统的续航能力。为了在实际应用中对超级电容的动态特性有深入了解,并充分实现系统仿真、优化超级电容的使用方法、优化混合动力系统结构设计及控制策略等目的,需要建立一个能够精确反映超级电容特性的模型[10]。

目前国内外超级电容模型多采用时变等效电路模型或在这个基础上进行简化的一些模型。相对于传统的线性时不变常系数模型,时变等效电路模型引入了随时间变化的参数(可变电容),基于此建立的模型就可以模拟超级电容在工作过程中的动态特性。然而,在参数辨识及仿真的过程中,模型的部分参数随充放电电流的不同变化较大。所以,当模型工作在电流变化范围比较大的情况下,就会导致仿真的数据与实验获取的数据相差较大,模型的可信度降低。

本文发现超级电容等效电路模型中一个电阻的参数值与充放电电流有着密切的关系,所以建立了变参数的扩展模型。通过Simscape Language在simulink中建立各元件的模型,同时使用Parameter Estimation得到模型中各参数的精确值。

1 超级电容等效电路模型

目前超级电容模型主要包括电化学模型和等效电路模型两种。电化学模型内部含有复杂的数学计算,同时计算结果为一组无法反映超级电容动态特性的静态值。所以,电化学模模型多用于理论分析。然而,等效电路模型以基本的电路元件为基础来模拟超级电容的动态特性,所以更适合实际应用场所。

目前,使用比较广泛的超级电容等效电路模型为时变等效电路模型。Zubieta等效电路模型是Bonert R于1997年提出的[11],如图1所示。其中Ci0为超级电容的等效电容,反映超级电容的储能特性;Rlea为超级电容的自放电电阻,是影响超级电容长时间储能效果的参数;Ci1·VCi反映超级电容在充电过程中的非线性特性;多RC分支反映停止充电后,超级电容内部电荷重新分配的的物理现象。

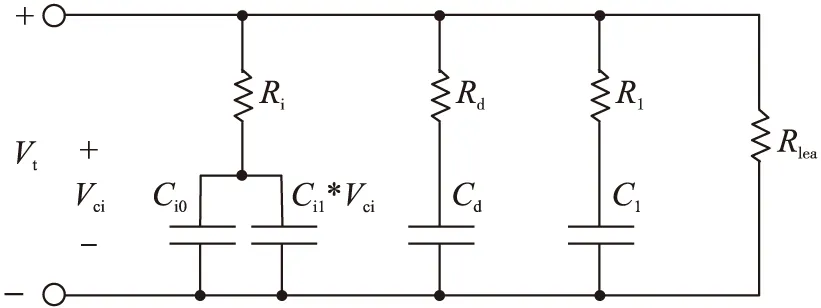
图1 Zubieta等效电路模型

2 超级电容的精确建模方法

2.1 模型参数辨识方法

Zubieta等效电路模型选定后,需要确定等效电路中各个参数的值。确定各元件特性参数的过程如图2所示。模型对恒流实验中的一个充放电的循环进行重复的仿真计算,同时将仿真计算的结果与实验数据测试得到的电压曲线进行比较,当两者的误差达到一定范围时,就可获取超级电容模型中各元件的特性参数。

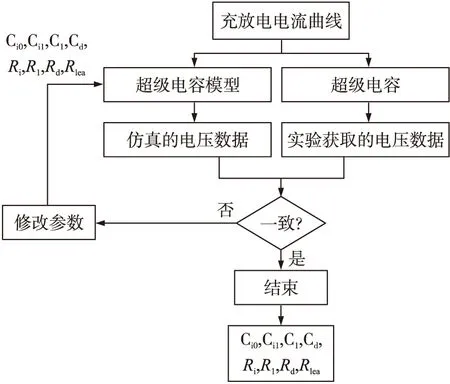
图2 参数辨识流程图

文中选用凯迈嘉华的UCP-3000F超级电容为研究对象,在恒温条件下获取超级电容的充放电曲线。实验中,分别采用10 A、25 A、50 A、75 A和100 A的电流进行充放电,得到相应的充放电曲线。按照上述参数辨识方法,选取Simulink中的Parameter estimation工具,得到各种充放电电流下对应的模型参数,见表1。为方便起见,这里将使用10 A充放电电流建立的超级电容模型表示为M10,同理可知M25,M50,M75,M100的含义。

表1 不同电流条件下的模型参数

2.2 传统辨识方法的缺陷

根据表1中的参数,建立对应充放电电流的超级电容模型。模型Mi(i=10,25,50,75,100)都使用图3中的90A电流进行充放电,将获得的仿真数据和实验数据进行比较。从图中可以明显发现,模型M50、M75、M100在90A的充放电条件下,仿真数据与实验获取的数据基本吻合,也就是说建立的模型是可信的。但是,模型M10和M25的仿真数据与实验获取的数据吻合度较低,尤其是模型M10仿真的数据与实验获取的数据相差较大。所以,在模拟超级电容小电流充放电时,使用传统方法获得的模型会出现精度不高的问题。通过上述分析,本文假设Zubieta模型的部分参数与电流的大小相关。

为了进一步研究参数Ci0,Cd,C1,Ri,Rd,R1,Rlea与电流的关系,需要更详细的充放电数据。因此,分别选择10A、20A、30A、40A、50A、60A、70A、80A、90A、100A的电流进行充放电实验。通过实验数据得到各种充放电电流下的模型参数。其中,Ci1是一个以电容终端电压为自变量的量,所以本文中采用中值求出Ci1;并在此基础上进行一定的修正,最后得出Ci1为345F。将得到的参数分别做成关于充放电电流的的曲线,如图4所示。

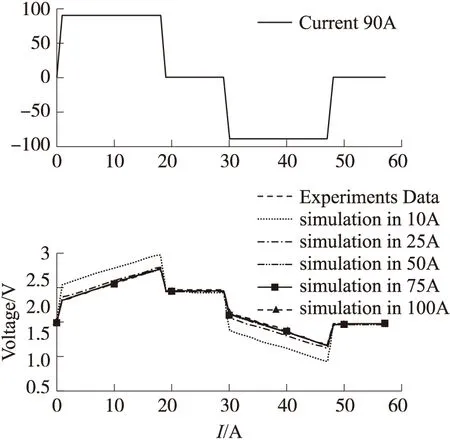
图3 90 A电流条件下的Mi(i=10,25,50,75,100)模型的仿真曲线

从图4可以发现,Zubieta模型中的各个参数与充放电电流都有一定的关系。其中Cd,Ci0,C1,Rd,R1,Rlea与电流成一种无规律的关系,但是Ri却随电流的增大而减小。因此,本文认为Ri是影响模型精确的因素。

由于参数Cd,Ci0,Cl,Rd,Rl,Rlea与电流没有规律可循,因此本文把模型Mi(i=10,20,30,40,50,60,70,80,90,100)中对应参数的平均值作为新模型的参数值。最后得到的参数值见表2。

表2 参数Cd,Ci0,Cl,Rd,Rl,Rlea

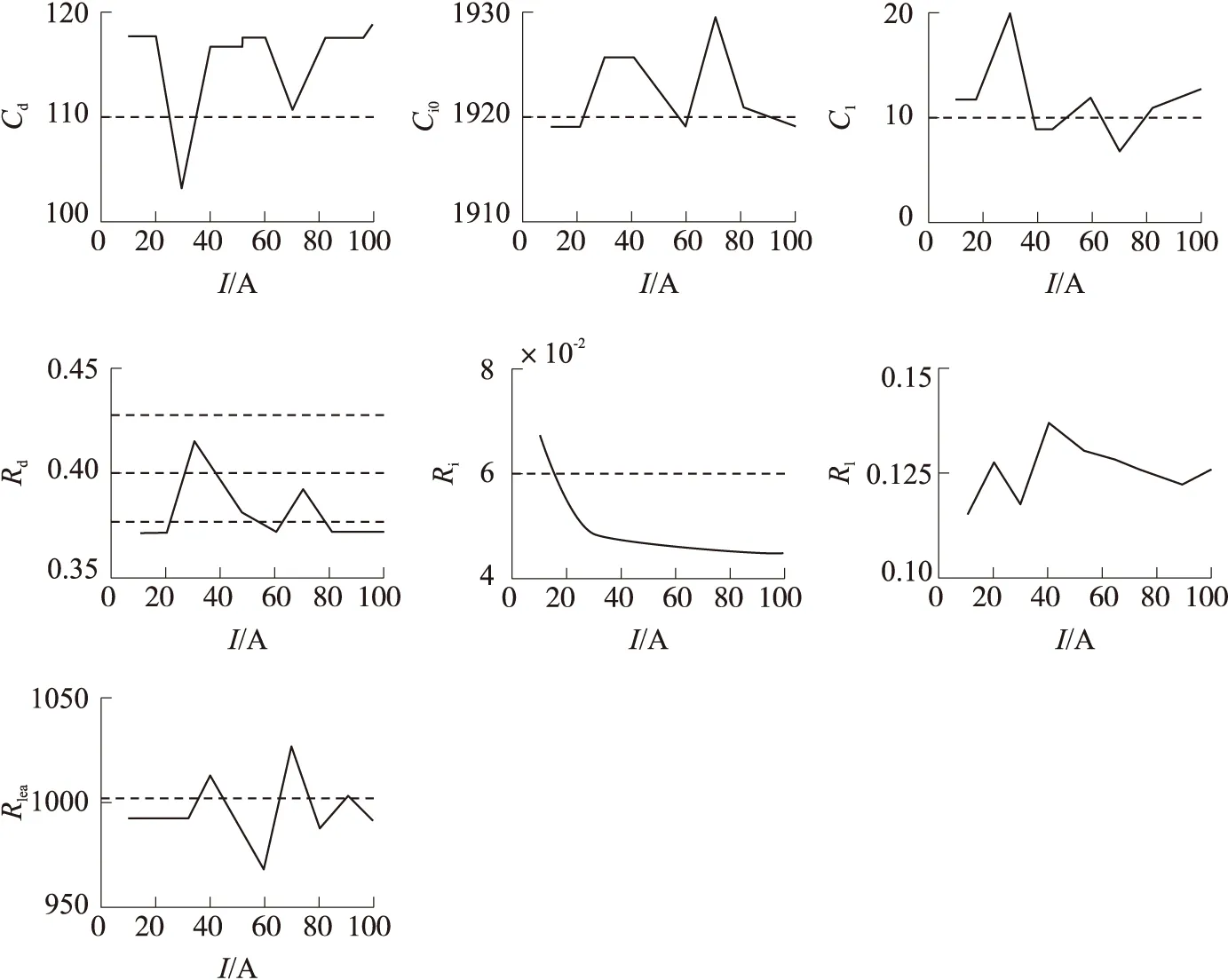
图4 不同电流下的的模型参数

2.3 基于Ri参数可变的精确辨识

图4中可以看出,参数Ri是随着电流的变化而变化的。由于参数Ri是动态变化的一个量,所以传统的模型将Ri固定为一个常量的模型精确度低,会出现模型仿真结果与实际不符的后果。本文采取多项式拟合的方法对参数Ri进行曲线拟合,拟合后的表达式为

Ri=p1x7+p2x6+p3x5+p4x4+p5x3+p6x2+p7x+p8

(1)

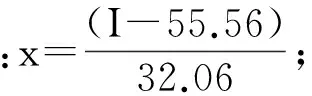
p1=-2.152 8×10-5;p2=8.653 3×10-5;

p3=-0.000 109 4;p4=3.755×10-5;

p5=-1.889 5×10-5;p6=8.974 2×10-5;

p7=-0.000 143 32;p8=0.004 593 8

其中:是实时采集的电流。p1、p2、p3、p4、p5、p6、p7和p8为常数。

图5 多项式拟合后的Ri参数

图5为多项式拟合曲线与原始参数曲线的比较图。从图中可以看出,使用多项式拟合后的曲线基本上可以准确代表原始参数曲线。所以Ri将随着输入电流动态改变,这样就提高了参数Ri的精度,进而提高了模型的准确性。

基于参数Ri随电流实时变化的特性,本文提出一种超级电容精确模型的新方法。在Zubieta等效电路模型的基础上,将固定电阻Ri替换为可变电阻。同时,可变电阻Ri的阻值是与充放电电流相关的变量。本文采用simulink中的SimscapeLanguage建立改进后的超级电容等效电路模型[12]。如图6所示。

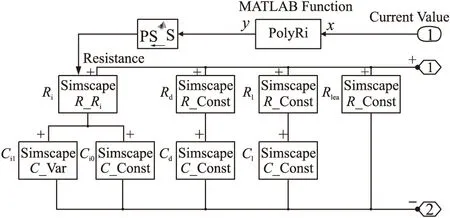
图6 改进后的单体超级电容模型

3 模型的验证

3.1 实验方法

本文使用凯迈嘉华的UCP-3000F超级电容作为实验的对象,超级电容的部分参数见表3。

表3 UCP-3000F超级电容超级参数

图7 实验平台

本文使用NEWARE 20 V-100 A的充放电机进行实验,为排除外界温度对超级电容动态特性的影响,所有实验都是在宏展仪器的恒温恒湿度箱中进行的,恒温箱的温度为20 ℃,相对湿度为50%,如图7所示。使用NI 6255 USB数据采集卡对超级电容的电压数据的采集,数据采样率为1 000 sample/s。

3.1 模型的验证

为验证本文提出的超级电容模型的可信度和精确度,进行变电流充放电和固定电流充放电的仿真,最后将仿真结果与超级电容以90 A充放电得到的实验数据进行对比分析。

图8为变电流充放电工况下,超级电容两端的电压残差图。绿线表示变化的充放电电流,电流的变化范围为0～100 V;蓝线表示参数Ri为常数时,实验过程中超级电容两端的电压与仿真模型两端的电压的差值,也就是电压残差;红线表示Ri为变参数时的电压残差。从图中可以看出,在30 A～100 A的充放电电流条件下,无论是固定的参数Ri还是用多项式拟合后的参数Ri,对模型的精确度影响不大。但是当充放电电流小于30 A时,影响却很大,见图8中的橙色圆圈部分。

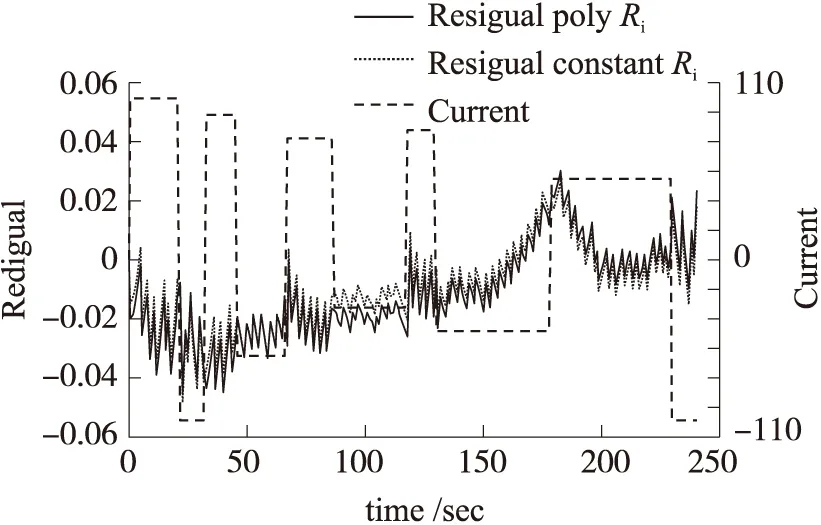
图8 变电流充放电实验数据下的仿真电压残差图

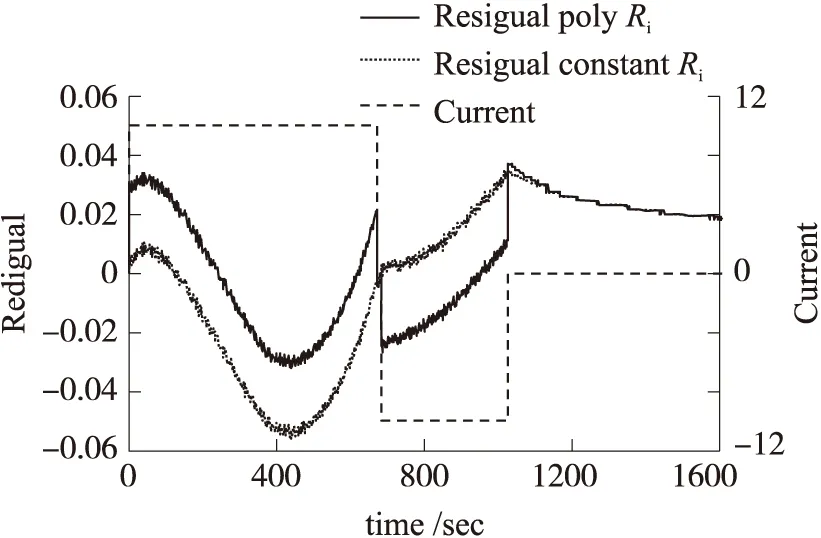
图9 10 A充放电实验数据下的仿真电压残差图

为了更进一步的研究模型参数Ri在小电流充放电时对模型精确度的影响,做了如图9所示的固定充放电电流10A下的电压残差图。图中,各线代表的含义与图8相同。由图中可以看出使用多项式拟合后的参数Ri建立的模型,其仿真结果(红线)与实验数据的电压残差为:稳态时0.03V左右,瞬态突变时0.025V。而使用常参数Ri后的电压残差为:稳态0.055V,瞬态0.035V。超级电容模型对于变电流工况有更好的适应性,主要是因为变电流可以减小极化内阻对压降的影响,所以瞬态误差比恒流充放电略微小一点。综合以上分析,在固定小电流充放电下,本文提出的基于可变电阻Ri的超级电容模型的精度比传统的模型提高了28%。

4 结论

在进行传统的超级电容模型参数辨识时发现,模型中各个参数与充放电电流都有一定的关系。其中,电阻Ri随着电流的增大而减小。本文将超级电容经典的时变等效电路进一步推广,引入一个与充放电电流相关的可变电阻Ri。采用多项拟合的方法将常参数Ri精确为一个随充放电电流变化的变参数。文中选用simulink作为工具,简化了参数辨识中的复杂计算,也提高了参数辨识的效率。本文最后,将仿真数据与实验数据对比,详细分析了变电流和固定小电流充放电下超级电容两端的电压残差。验证结果表明,基于可变电阻Ri的超级电容模型是可信的,提高了超级电容模型在小电流充放电下的精度,可以更准确的描述超级电容工作的动态过程。

[1] 苏波,李艳秋,于红云,等.从环境中获取能量的无线传感器节点[J].传感技术学报,2008,21(9):1586-1589.

[2]Rotenberg D,Vahidi A,Kolmanovsky I.Ultracapacitor Assisted Powertrains:Modeling,Control,Sizing,and the Impact on Fuel Economy[C]//Control Systems Technology.IEEE Transactions on,2011,19(3):576-589.

[3]Eddahech A,Ayadi M,Briat O,et al.Multilevel Neural-Network Model for Supercapacitor Module in Automotive Applications[C]//Power Engineering,Energy and Electrical Drives(POWERENG),2013 Fourth International Conference on IEEE,2013:1460-1465.

[4]任喜国,杨承志.超级电容直流电源的研究[J].科学技术与工程,2013,13(19):5642-5648.

[5]赵坤,王迅,杨中平,等.超级电容储能系统抑制直流牵引网压波动的研究[J].北京交通大学学报,2011,35(2):133-136.

[6]Yang H,Zhang Y.Evaluation of Supercapacitor Models for Wireless Sensor Network Applications[C]//Signal Processing and Communication Systems(ICSPCS),2011 5th International Conference on IEEE,2011.

[7]Weiran X Q B H Z.EDLC Charging Performance for Microgrid Applications[J].东南大学学报(英文版),2010,26(3):415-420.

[8]王玮,沈继忠,董利达.自供电磁阻车辆检测节点设计[J].传感技术学报,2013,26(12):1734-1739.

[9]李兴圣,李平,文玉梅,等.一种磁电换能器及其能量管理电路研究[J].传感技术学报,2009,22(7):954-960.

[10]王红梅.混合动力挖掘机用超级电容的建模与参数辨识[J].电源技术,2014,38(8):1504-1506.

[11]Zubieta L,Bonert R.Characterization of Double-Layer Capacitors for Power Electronics Applications[J].Industry Applications,IEEE Transactions on,2000,36(1):199-205.

[12]Faranda R,Gallina M,Son D.A New Simplified Model of Double-Layer Capacitors[C]//Clean Electrical Power,2007.ICCEP’07.International Conference on IEEE,2007.

Accurate Modeling of Supercapacitor Based on Variable Resistor*

SUOChunguang1*,LIUShihua1,ZHANGWenbin1,SUShi2,YANYuting2,YANGYang2

(1.Kunming University of Science and Technology,Kunming 650000,China;2.Yunnan Electric Power Test and Research Institute(Group),Kunming 650063,China)

Supercapacitor is widely in many applications,and accurate models will reflect the information just like the real situation of the practical application and provide a basis to users.However,the relationship between each parameter and the charge and discharge currents is ignoring in the traditional modeling.So the accuracy of the model is lower.This paper presents an extended model in which the constant resistance is replaced by a variable resistor with the current changes.The experimental data was obtained by a charge and discharge experiment,and the Parameter Estimation was used to identify the values of the model parameters.The dynamic value of the variable resistor was got in polynomial fitting method.The results showed that characteristics of the extended dynamic supercapacitor model was more accurate.

supercapacitor;equivalent circuit model;parameter identification;dynamic model