基于VFD滤波器的测控信号动态信息加载方法*

李伟，杨文革，赵江

(装备学院 光电装备系，北京 101416)

基于VFD滤波器的测控信号动态信息加载方法*

李伟，杨文革，赵江

(装备学院 光电装备系，北京 101416)

针对动态性能测试中的测控信号大动态信息加载问题，提出了一种基于VFD滤波器的加载方法。该方法采用整点延时对原静态信号实现整数倍采样间隔延时，然后采用VFD滤波器对整点延时信号实现高精度小数延时，从而得到精确延时信号，实现测控信号的大动态高精度模拟。仿真分析表明，该方法不但能实现测控信号的大动态高精度模拟，且能适应于不同体制测控信号的动态模拟，为动态性能测试过程中的静态测控信号加载动态信息提供了一种方法。

VFD滤波器；动态加载；小数延时；动态模拟；大动态

0 引言

新型的飞行器测控(telemetry,track and command,TT&C)试验中，为检测飞行器上应答机与地面测控设备之间的兼容性，需对其进行对接试验。试验中，动态性能测试是系统性能测试的一项重要指标，传统的动态性能测试是通过飞机挂载应答机进行校飞试验，但由于飞机速度偏低等局限，导致校飞试验无法检测测控设备在高速运动状态下的动态性能[1]；另一种是基于硬件平台对存储的静态测控信号进行延时存储等处理，模拟飞行器在运动状态下的动态信号，但其只能实现整数采样周期的延时，模拟的动态精度较低。

在引入上下变频和存储转发设备的对接过程中，为实现应答机和测控设备的动态性能检测，需对存储的中频数字静态测控信号加载动态信息，模拟动态测控信号。针对此应用，本文提出了一种基于VFD(variable fractional delay)滤波器的测控信号动态模拟方法，并对其进行了分析与仿真验证。结果表明，该方法能适应多种测控体制信号的动态模拟，且能实现大动态特性的高精度模拟。

1 动态信息加载原理与实现方案

在理想情况下，接收信号Sr(t)和发射信号Ss(t)的关系可表示为

(1)

式中：τ为信号传输延时；k为信号的幅度衰减。

由式(1)可知，动态信号模拟时加载的动态信息包括功率(即幅度)变化信息和延时变化信息。功率变化信息主要与电磁波传播的距离和信道特性有关，在实际的模拟中可以采用功率衰减器实现[2]，其实现方法相对简单，因此本文重点讨论延时信息加载。

由于滤波器对通过的信号具有群延时效应，且群延时在通带内线性可控[3]，因此可通过精确控制数字滤波器的群延时，实现延时信息加载，但常规的有限长单位冲激响应(finite impulse response,FIR)滤波器的群延时为定值，且延时为采样间隔的整数倍。此种滤波器用于动态模拟时精度低，且需要根据延时信息不断改变滤波器参数，系统实时性要求较高。

为解决上述滤波器小数群延时连续可变问题，C.W.Farrow提出了一种Farrow结构的可变小数延时(variable fractional delay，VFD)滤波器[4]。Farrow结构滤波器的频率响应与小数延时有关，但滤波器的系数与延时无关，因此在实际应用中，只需计算存储一次滤波器系数即可。由于该方法在实时处理中有着不可比拟的优越性，使得该方法在其后二十年里得到深入研究和开发，并广泛应用于回波对消、宽带雷达波束形成、数字信号合成等方向[5-6]。VFD滤波器对信号进行延时处理的不足之处是，原数据需先进行整数点延时处理。

根据VFD滤波器的特性，拟定延时滤波器实现动态信息加载方案如图1所示。

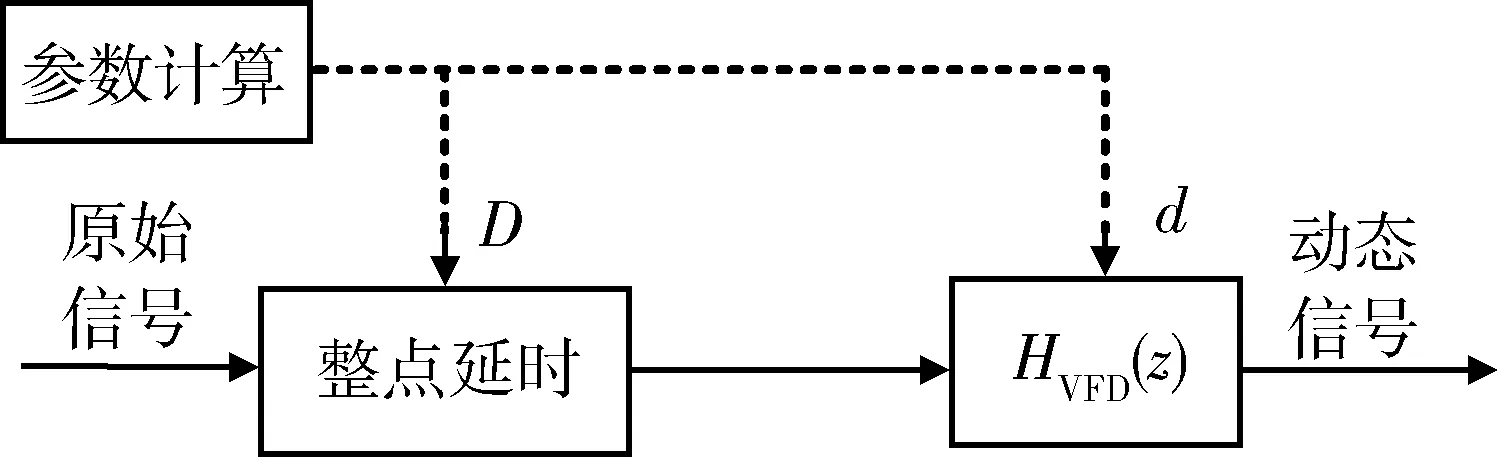
图1 基于延时滤波器的动态信息加载方案Fig.1 Dynamic loading scheme based on VFD filter

参数计算模块根据轨道参数计算出原始数据对应的精确延时，并将其延时分为整数倍采样间隔延时D和小数倍采样间隔延时d(0≤d<1)2部分。整点延时模块根据参数D对原数据先进行整点延时，然后再通过VFD滤波器加入小数延时，即实现对原数据加载动态延时信息。整点延时可采用文献[7]介绍的方法，此处不再重复，后文主要介绍使用VFD滤波器实现精确的小数延时。

2 延时滤波器的设计与仿真

假设x(t)是一个连续时间信号，对x(t)进行τ延时处理后可得到其延时信号为

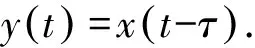
(2)

分别对x(t)，y(t)进行采样得到离散信号x(n)和y(n)，则

(3)

式中：Dτ=τ/Ts，Ts为采样周期，通常延时值τ并不是整数倍的抽样间隔，则数字延时值Dτ可以表示为Dτ=⎣D」+d，⎣D」表示小于Dτ的最大整数，d表示Dτ的小数部分。

对延时后的输出信号y(n)进行离散时间傅里叶变换(DTFT)得到[8]：

(4)

式中：Y(ω)，X(ω)为别为y(n)和x(n)的离散时间傅里叶变换。

由式(4)可知，延时处理的系统响应函数可以表示为

(5)

由于理想滤波器在物理上是不能实现的，一般采用N阶有限长FIR滤波器h(n)逼近hid(n)的方法来实现[9]，系统对应的频率响应为

(6)

如果用小数延时d的M阶多项式近似滤波器系数h(n)，则可以将参数d从滤波器系数中分离出来，此处考虑到多项式的收敛性，故只考虑延时Dτ的小数部分，式(6)中的h(n)可以定义为[10-11]

(7)

将式(7)代入到(6)中可得

(8)

分析式(8)可知，H(z,d)可看作是小数延时d对M个N阶直接型FIR滤波器Cm(n)输出的加权和。虽然滤波器的频率响应和小数延时d有关，但各分支滤波器的系数与延时d取值无关，因此当延时值d改变时并不需重新计算或加载滤波器系数。

本文根据Deng T. B.在文献[10]提出的基于加权最小二乘法(weighted least square,WLS)算法的VFD滤波器设计方法，设计滤波器阶数N=65，M=8的VFD滤波器。WLS算法定义频率响应加权误差函数为

(9)

(10)

式中：W1(ω)和W2(p)分别为

(11)

(12)

其中，为表达方便引入自变量p(p=d)。定义绝对误差表达式[12]为

(13)

仿真得到的VFD滤波器幅频特性如图2所示。

理想的VFD滤波器的幅度响应在整个频带范围内为定值1，且不随着延时大小而变化，但由图2中VFD滤波器幅频响应与延时的关系可知，实际的VFD滤波器不可能实现全频带内理想的全通，因此在高频部分出现了较大偏差。由图2还可以看出，在延时为0或0.5个采样点间隔时，幅频响应较为接近理想值。图3给出了仿真得到的VFD滤波器和理想VFD滤波器频率响应的绝对误差曲线，从图中可以看出，在0～0.9π的通带范围内，频率响应的绝对误差基本维持在-80 dB以下，表明仿真得到的VFD滤波器与理想的VFD滤波器近似程度很好。图4给出了仿真得到的滤波器的群延时特性。

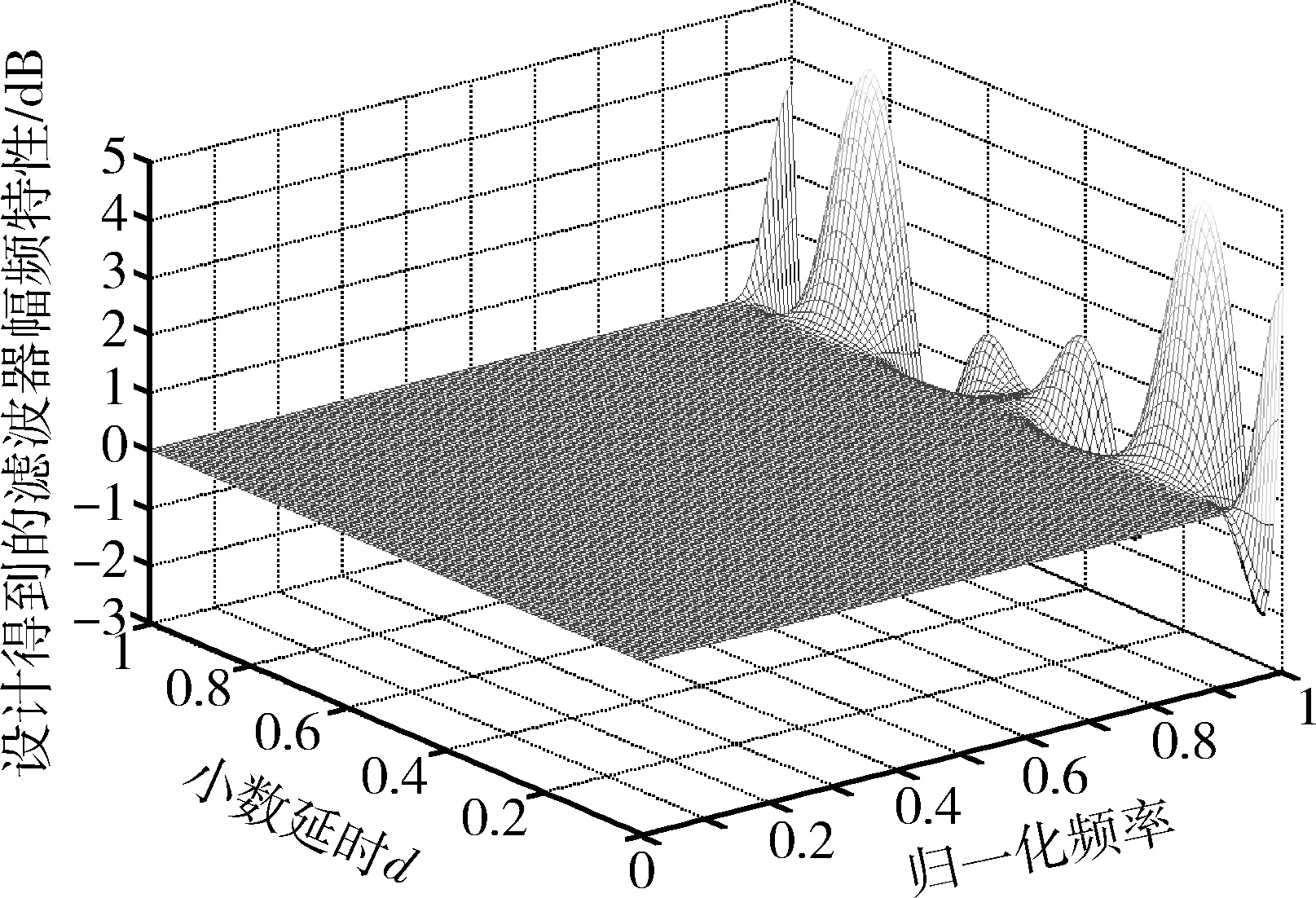
图2 仿真所得VFD幅频响应与延时关系Fig.2 Magnitude response of simulated VFD filter

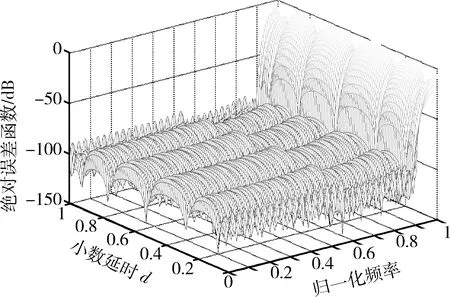
图3 频率响应的绝对误差Fig.3 Absolute error of variable frequency response

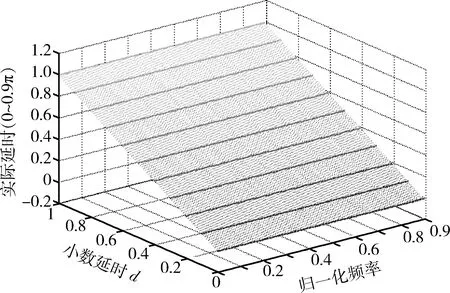
图4 VFD滤波器群延时Fig.4 Variable fractional delay of VFD filter

从图4中可以看出，滤波器的群延时随着输入的小数延时值d的改变而改变，且在0～0.9π的通带范围内，群延时和理想的群延时基本相等。图5给出了0～0.9π间的群延时误差曲线，从图中可以看出，群延时误差最大约为4×10-3个采样间隔。

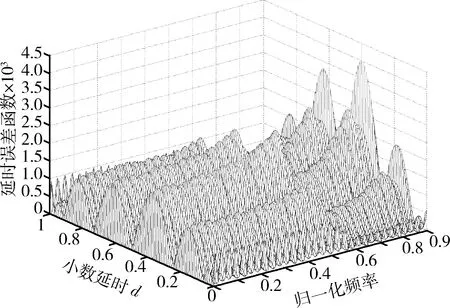
图5 小数延时误差Fig.5 Absolute error of variable fraction delays

3 精度分析

由加载方案原理可知，使用本节所述方法加载延时信息时，加载的延时信息的精度主要取决于延时信息的精度、整点延时精度和滤波器实现的小数延时的精度。由于延时信息的精度取决于动态参数的解算精度，在此不予考虑，又因为现有的整点延时方法已相当成熟，且精度可以达到ps级，因此不考虑整点延时精度对距离的影响，此处只考虑滤波器群延时精度对距离信息的影响。

从图5可以看出，使用VFD滤波器实现延时信息加载的精度最低约为4×10-3个采样间隔，则延时信息加载精度ΔT和距离信息加载精度可分别写为

(14)

ΔR=cΔT.

(15)

如果采样间隔按1/56 MHz计算，光速c取3×108m/s，则距离信息加载精度ΔR≤0.022 m。

由距离信息加载精度结论可知，基于延时滤波器动态信息加载得到的动态信号，任意两数据点之间的延时误差不超过2ΔT，结合多普勒与延时信息的关系可知，基于VFD滤波器的动态信息加载的多普勒信息加载精度为

(16)

假设延时误差ΔT取其最大值4×10-3Ts，积分时间仍按t2-t1=0.05 s，按照式(16)计算可知，采用延时滤波器加载动态信息时，多普勒信息加载精度为0.2 Hz。根据多普勒与速度的关系可知，速度信息加载精度为0.2×10-2m/s(f0取70 MHz)。

4 仿真验证

为验证动态信息加载方案的有效性，现采用标准TT&C信号进行仿真实验，仿真参数如表1所示。

此处对比信号为文献[7]所述方法得到的整点延时信号和直接生成的标准延时信号，仿真结果如图6所示。

从仿真时域效果来看，虽然整点延时信号与标准延时信号较为接近，但仍存在明显误差，而经整点延时和VFD滤波器得到的动态信号与标准延时信号一致性良好；从仿真频域效果图来看，本文所述方法得到的动态信号多普勒与原信号的频差为-800 kHz，与加载的动态信息一致(fd=-800 kHz)。以上结果表明，基于VFD滤波器的动态信息加载方案可正确实现动态信号模拟，且效果优于整点延时的动态信息加载效果。

表1 仿真参数Table 1 Simulation parameters

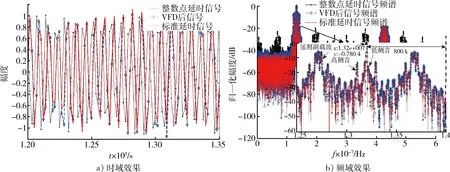
图6 TT&C信号动态加载效果图Fig.6 Dynamic loading results of TT&C signal

5 结束语

本文结合传统的整点延时与VFD滤波器，成功实现了较高精度的测控信号大动态模拟，为测控设备动态性能测试中的动态信号模拟提供了一种有效的解决方案。仿真结果表明，本文采用的方法能够较好地实现测控信号大动态模拟。结果还表明，采用该方法模拟测控信号动态时，不需要限制原信号格式，相比传统解调模式的动态信号模拟具有更好的适应性。

[1] 李伟, 杨文革, 程艳合. 扩频测控信号大动态信息高精度加载方法[J].飞行器测控学报, 2013, 32(4): 321-326. LI Wei, YANG Wen-ge, CHENG Yan-he. Approach of Accutate Loading of High Dynamic for Spread Spectrum TT&C Signals[J]. Journal of Spacecraft TT&C Technology, 2013, 32(4): 321-326.

[2] 邓永铭. 采用开环模式实现深空动态模拟源设计[J]. 电讯技术, 2009, 49(7): 73-76. DENG Yong-ming. Implementation of Dynamic Simulating Source Design by Using Open Loop Mode [J]. Telecommunication Engineering, 2009, 49(7): 73-76.

[3] 胡广书. 数字信号处理——理论、算法与实现[M]. 北京: 清华大学出版社, 2003. HU Guang-shu. Digital Signal Processing[M]. Beijing: Tsinghua University Press, 2003.

[4] FARROW C W. A Continuously Variable Digital Delay Element[C]∥IEEE International Symposium Circuits and Systems (ISCAS’88),Espoo:IEEE,1988, 6: 2641-2645.

[5] 陈彩莲, 于宏毅, 罗柏文，等. 一种灵活高效的分数延迟数字滤波器[J]. 信息工程大学学报, 2009, 10(4): 457-460. CHEN Cai-lian, YU Hong-yi, LUO Bo-wen, et al. Flexible and Efficient Implementation for Fractional Delay Digital Filter[J]. Journal of Information Engineering University, 2009,10(4): 457-460.

[6] Jong-Jy Shyu, Soo-Chang Pei, Cheng-Han Chan. Minimax Phase Error Design of Allpass Variable Fractional-Delay Digital Filters by Iterative Weighted Least-Square Method[J]. Signal Processing，2009, 89(9): 1774-1781.

[7] 雷鸣, 李珂. 采用闭环双口RAM实现深空动态模拟源的设计[J]. 电讯技术, 2011, 51(3): 33-36. LEI Ming, LI Ke. Design of Dynamic Simulating Source for Deep Space Communication by Using Close Loop Dual-Port RAM[J]. Telecommunication Engineering, 2011, 51(3): 33-36.

[8] Jong-Jy Shyu, Soo-Chang Pei. A Generalized Approach to the Design of Variable Fractional-Dealy FIR Digital Filters[J]. Signal Processing, 2008, 88(6): 1428-1435.

[9] Timo I Laakso, Vesa Valimaki, Matti Karjalainen, et al. Splitting the Unit Delay-Tools for Fractional Delay Filter Design[J]. IEEE Trans. Signal Processing, 1996,13(1): 30-60.

[10] DENG Tian-bo. Discretization-Free Design of Variable Fractional-Delay FIR Digital Filters[J]. IEEE Trans. Analog and Digital Signal Processing, 2001, 48(6): 637-644.

[11] DENG Tian-bo. Symmetry-Based Low-Complexity Variable Fractional-Delay FIR Filter[C]∥International Symposium on Communications and Information Technologies 2004(ISCIT 2004), Sapporo, Japan, 2004:194-199.

[12] TARCZUNSKI P J, CAIN G D, HERMANOWICZ E, et al. WLS Design of Variable Frequency Response FIR Filters[C]∥ IEEE Trans. Circuits and Systems, Hong Kong, 1997：2244-2247.

Approach of Dynamic Loading for TT&C Signal Based on VFD Filter

LI Wei, YANG Wen-ge, ZHAO Jiang

(Academy of Equipment，Department of Optical and Electrical Equipment，Beijing 101416，China)

A processing method based on variable fractional delay (VFD) filter is proposed to implement the accurately loading high dynamic for TT&C signal．The method could achieve the high accuracy and high dynamic simulation for the TT&C signal, which adopts the way of store-delay to implement integer delay for the static data, and uses the VFD filter to implement high accuracy fractional delay for the integer delay signal．Simulation results show that the proposed method can not only accurately and commendably implement loading high dynamic for telemetry, track and command (TT&C) signal, but also suit for dynamic simulations of signals of different forms．It provides a good way for dynamic simulation in the dynamic performance test of TT&C equipment．

variable fractional delay(VFD) filter；loading dynamic；fractional delay；dynamic simulation；high dynamic

2014-02-16；

2014-06-05

李伟(1989-)，男，湖南衡阳人。硕士生，主要研究方向为航天测控和数字信号处理。

通信地址：101416 北京市怀柔区3380信箱装备学院研4队 E-mail：loxwei@163.com

10.3969/j.issn.1009-086x.2015.03.026

TN713;V556；TP391.9

A

1009-086X(2015)-03-0146-05