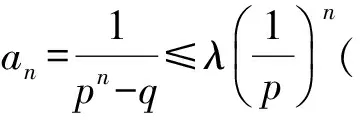基于学生视角设计教学 实现难点有效突破
——有感于一节高三数列专题复习课
2015-05-04刘美良鲁迅中学柯桥校区浙江绍兴312000
●刘美良 (鲁迅中学柯桥校区 浙江绍兴 312000)
基于学生视角设计教学 实现难点有效突破
——有感于一节高三数列专题复习课
●刘美良 (鲁迅中学柯桥校区 浙江绍兴 312000)
道法自然,是道家思想的一个基本观点,也是平常为人处事的一个基本原则.在高三的复习教学中更应如此,即遵循学生的认知规律,尽力站在学生的角度设计教学,让数学知识、方法在学生的心里自然地生发出来,从而实现难点的有效突破.
1 问题背景
有关数列和式不等式的证明已成为高考、模考命题的新热点.对于数列和式不等式的证明,高三学生普遍感觉束手无策,无章可循.为此,备课组组织了一次集体备课,集中研讨有关数列和式不等式的证明问题,并由同组的一位年青教师执教,公开展示了一节“探寻一类数列和式不等式的求证策略”专题复习课.整节课的设计基于学生视角,层次清晰,教学自然.笔者感触颇深,特整理成文与同行共赏.
2 教学片断(简录)
师:2015年浙江省数学高考对数列这部分内容的考查难度明显提升,这从样卷和各地模考试题中已见端倪,尤其是数列中一类和式不等式的放缩问题,更是大家“心中的痛”(学生会心地笑).今天我们一起直面这类问题,探寻其求证的方法(展示课题并出示问题).
问题 已知数列{an}的前n项和Sn满足:an+Sn=1,n∈N*.
1)求数列的通项公式;
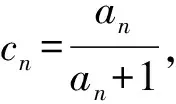
师:请同学思考并求出通项an.
(稍后有学生发言.)
师:考虑很全面,退位作差时初始检验不能忘记.第2)小题数列{cn}的和能求吗?
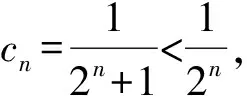
师:通过减1将分式放大,并转化为基本数列——等比数列求和,很自然、很合理!
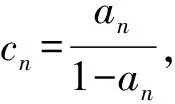
师:是2类基本数列:等差、等比数列的求和吗?若不是,怎么转化?请大家思考、讨论,并发表个人想法.
(不一会儿有学生示意.)
生:应该转化为等比数列求和.因为
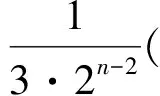
所以Tn=c1+c2+…+cn<
师:这位同学的直觉思维很强,有相当的功力!但这一步对部分同学来说有点突兀,老师想听听其他同学的想法?
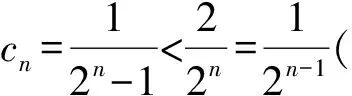
师:这是运用什么原理或性质?
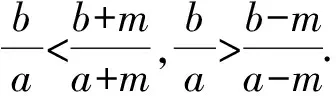
师:根据糖水浓度不等式,将原式转化为等比数列模型,进而求和,结论更精准.这说明:放缩要有“度”哦!还有其他想法吗?
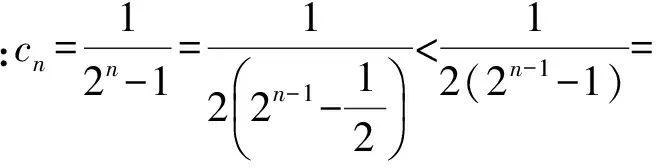
师:借用迭代法转化为递推模型达到放缩.请大家谈谈以上3种方法的异同之处并总结.
生:共同点是将数列{cn}通过放缩转化为等比数列的模型;不同的是转化的方式不同,并且2个等比数列的公比、首项不同.
师:能对上述数列{cn}模型进行一般化推广吗?请大家讨论,总结放缩方法.
(学生交流,师生共同总结、完善.)
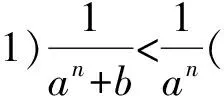
2)构造递推数列:
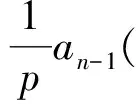
从而
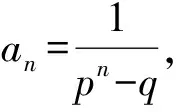
①当n≥2时,pan 师:请说说你的想法.以上的模型还能用吗? (经思考和对比后,学生发言.) 师:哪位同学能把首项搞定? 生(脱口而出):那就待定呗! 师:怎么待定呢?请继续思考,讨论! 生:应该是恒成立问题. (学生一下子豁然开朗,情绪高涨!) 生:那就分离变量吧! 生:当n≥1或n≥2时都有可能吧? 经过分组讨论,整理形成以下的解法: f(n)max=f(1)=2, 于是λ可取2.即当n≥1时,有 因此Tn=c1+c2+…+cn< 因此Tn=c1+c2+…+cn≤ 经过思考与交流,学生很快完成以下变式3的解答: 因此Tn=c1+c1+…+cn≤ 自编题2(课后) 已知数列{an}的前n项和Sn满足:2Sn=an+1-2n+1,n∈N*,若a1,a2+5,a3成等差数列. 1)求数列{an}的通项公式; f(n)max=f(1)=3, 于是λ可取3,因此 3.1 复习教学设计应基于学生的“原生态” 人教社章建跃老师指出:教学设计的首要问题是理解数学,基于学生的原认知、原生态;设计思想是让学生领悟到知识、方法、技巧的来源.课程标准也明确指出,数学教学应揭示数学概念、法则、结论的发展过程,体会蕴含其中的思想方法,追寻数学发展的历史足迹. 因此,数学教学设计应从学生的知识水平、认知特点、学习困惑、思维习惯等方面进行,注意知识与方法产生的自然性与合理性.本节课从问题1入手,让学生观察发现结构特征,形成问题解决的转化方法;变式1的教学,教师放手发动学生分析问题,共同寻求问题解决的途径,达到一题多解.这2个问题看似简单,实质上对数列和式不等式的放缩解决起到了良好的导向作用,实现“多解归一”,即转化为等比数列求和的思维目标,为后续问题的解决指明了方向,架设学生思维攀爬的“脚手架”.在这个过程中,既有对不等式基本性质、糖水不等式、数列迭代等知识的唤醒、运用,又在无形中渗透了转化化归的数学思想.所谓有化有归,突出了本节课的主题,使本节课的设计贴近学生、层次清晰、灵活本真、自然生态. 3.2 复习教学应揭示问题的本质 3.3 复习课教学应让学生在课堂上生长 记得有一位语文老师说:课堂呈现的不仅仅是“鲜花”,还应该有“花开的声音”.课堂上最美的声音是学生生命里“拔节”的声音.高三是知识、能力长得最快的“季节”,复习课堂是学生能力的主战场.“如何让学生在课堂上快速生长”已成为教学设计、教学活动开展需要思考的重要课题.那种“满堂灌、一言谈、教师讲、学生听”的复习模式应扔进时代的垃圾箱,而应创设民主、和谐、生态的教学氛围,教师要“闭口”,学会等待、敢于放手.给学生自主思考的时间、空间,让其发现解决问题的切入口、方法源,促使学生领悟知识,内化活动经验,并尝试改题、编题,使能力在课堂上生长. [1] 严士健,张奠宙,王尚志.数学课程标准(实验)解读[M].南京:江苏教育出版社,2004. [2] 潘彩,王弟成.春风化雨 润物无声[J].数学通讯,2014(12):63-68.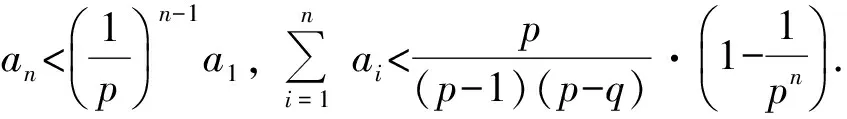
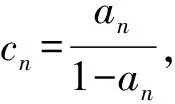
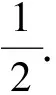
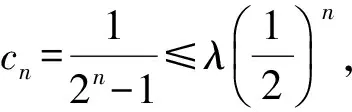
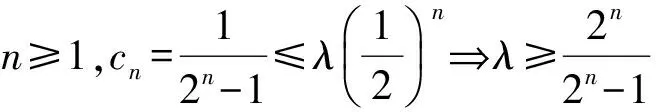
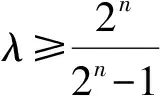
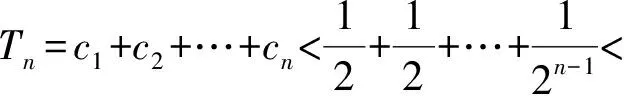
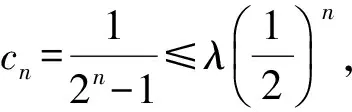
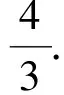
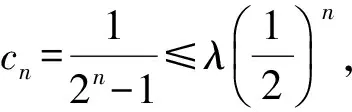
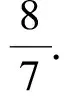
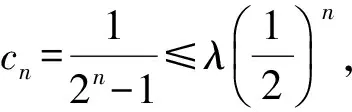
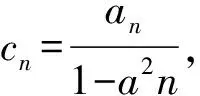
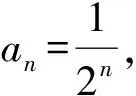
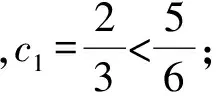
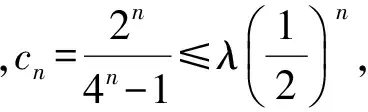
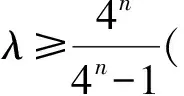
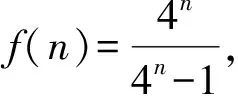
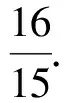
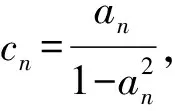
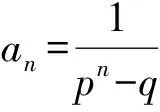
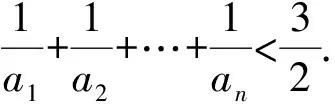

3 感悟与体会