利用空间向量特殊化与几何性质解立体几何中的轨迹问题

●李芳奇 (温州市第二高级中学 浙江温州 325000)

●唐恒钧 (浙江师范大学教师教育学院 浙江金华 321004)

利用空间向量特殊化与几何性质解立体几何中的轨迹问题

●李芳奇 (温州市第二高级中学 浙江温州 325000)

●唐恒钧 (浙江师范大学教师教育学院 浙江金华 321004)

高考数学命题重视知识的交叉渗透，在知识网络的交汇点设计试题.近几年来，各省市数学高考试题以立体图形为载体的轨迹问题时有出现，将立体几何和解析几何巧妙地整合在一起，立意新颖，综合性强.这类试题由于知识点多，数学思想和方法考查充分，因此求解比较困难，通常需要学生有较强的空间想象能力.而空间向量法作为一种将立体几何问题转化为代数运算的方法，极大程度地降低了对学生空间想象能力的要求.此外，教师在教学中也应牢抓图形的几何特征，培养学生的空间思维能力.本文以一堂课的教学实录为例，以期抛砖引玉.

1 问题提出

例1 设m是平面α内的一条定直线，P是平面α外的一个定点，动直线n经过点P且与m成30°角，则直线n与平面α的交点Q的轨迹是

( )

A．圆 B．椭圆 C．双曲线 D．抛物线

这是笔者所在学校期末试卷中的一道选择题，正确答案为C.该题的正确率在50%左右，答不出来的学生普遍反映无从下手，只能凭感觉猜.笔者调查5位正确作答的学生，其中有4位给出的方法是空间向量建系，只有1位学生是根据直线n的几何模型特征，得知它是一个圆锥面从而求解.

由于选择题答案的唯一确定性，选择空间向量建系法的学生，在处理此问题时就显得比较灵活，可以以此为依托，求得轨迹方程，从而得知是什么类型的曲线.笔者进而追问他们是如何建系的.

生1：以平面α所在的面建立xOy平面.

师：直线m的方向向量如何表示？点P的坐标呢？

生1：设直线m的方向向量为m=(1,0,0)，P(1,1,1)，Q(x,y,0)，则

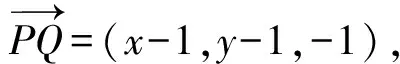
从而

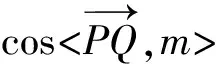
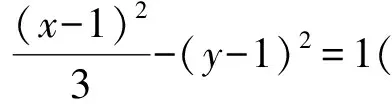
师：这是双曲线的标准方程吗？

生1：好像……不是，是经过平移后的双曲线.

生2：选点P为(0,0,1)更方便，此时

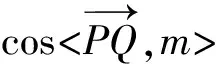
化简得

师：对于选择题而言，用最快速、便捷的方法求解乃是上上策.生1已经很棒，当然还是选生2的方法更好！大家再仔细读题“动直线n经过点P且与m成30°角”，某直线过定点与一条定直线成定角的轨迹是什么？此类问题在历年高考中屡有涉及.

2 高考链接

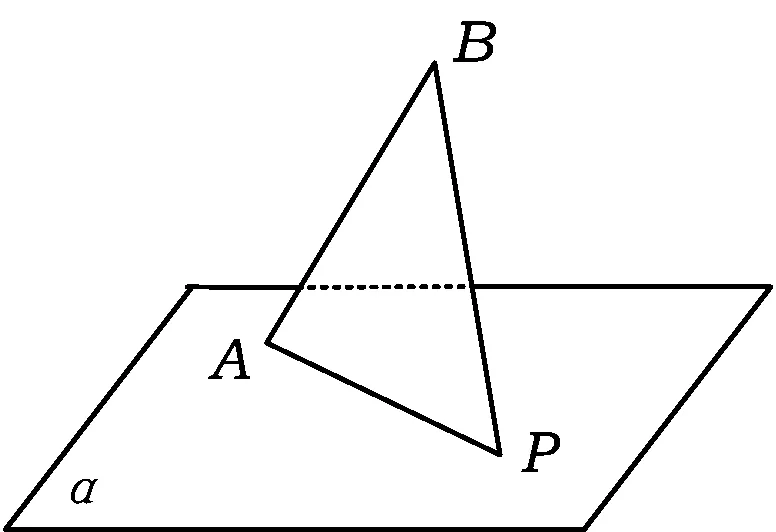
图1

例2 如图1，AB是平面α的斜线段，A为斜足.若点P在平面α内运动，使得△ABP的面积为定值，则动点P的轨迹是

( )

A．圆 B．椭圆

C．1条直线 D．2条平行直线

(2008年浙江省数学高考理科试题第10题)

分析 由于线段AB是定长线段，且△ABP的面积为定值，因此动点P到线段AB的距离也是定值，可知点P在以AB为轴的圆柱侧面上.又因为点P在平面内运动，所以相当于用一个与AB不垂直的平面去截圆柱，得到的截痕为椭圆，即点P的轨迹是圆柱侧面与平面α的交线.

类似的还有2006年北京市数学高考理科试题第4题.

例3 平面α的斜线AB交α于点B，过定点A的动直线l与AB垂直，且交α于点C，则动点C的轨迹是

( )

A．1条直线 B．1个圆

C．1个椭圆 D．双曲线的1支

(2006年北京市数学高考理科试题第4题)

分析 由直线l始终与AB垂直，可知l的运动轨迹是直线AB的垂面β，而点C又在平面α内，因此点C的轨迹是2个平面的交线.故选A.

例3变式 直线AB与平面M成α角，交平面M于点B，直线PA始终与直线AB保持β角，点P在平面M上，求点P的轨迹方程.

根据人教版教科书选修2-1对圆锥曲线定义的介绍，可知：1)当α≠90°,β=90°时，动点P的轨迹是1条直线.2)当α=90°,β≠90°时，动点P的轨迹是1个圆.3)当α≠90°,β≠90°时，是1个圆锥面，更具体地说，当α=β时，为抛物线；当0<α<β时，为双曲线；当β<α<90°时，为椭圆.

经过例3变式题的研究之后，学生很容易利用所学知识得到：在例1中，不论2条直线m,n成多少度角，其本质是2个圆锥的轴与截面是平行的，因此所得的轨迹为双曲线.

3 拓展应用

例4 如图2，在底面为平行四边形的四棱锥P-ABCD中，E,F分别是棱AD，BP上的动点，且满足AE=2BF，则线段EF中点的轨迹是

( )

A．1条线段 B．1段圆弧

C．抛物线的一部分 D．1个平行四边形

(2015年浙江省普通高中数学学业水平考试第25题)

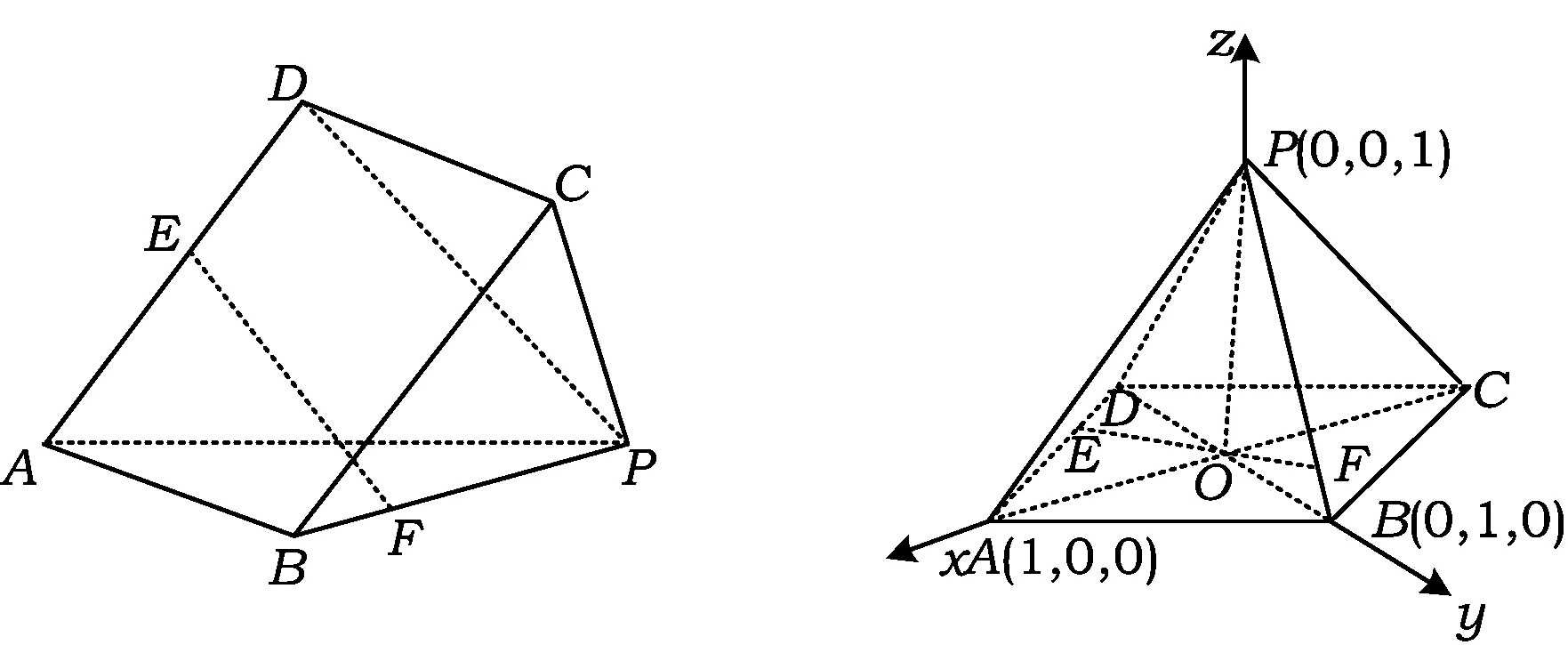
图2 图3

不同于前面例题中涉及到的角度问题，例4是关于长度关系的题型.学生思考片刻后，大部分学生表示毫无头绪，也有小部分学生尝试采用空间向量建系法.

师：如何建系？底面为平行四边形，建系起来貌似不那么方便呀.

生3：这是选择题，可以取特殊的四棱锥！

师：看来例1给了大家很大的启发，学以致用，很好！选何种四棱锥？如何建系？

生3：选最特殊的正四棱锥，以正方形ABCD为底面画图建系(如图3).

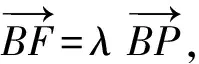
师：我们学过此类方程吗？

生4：没有，不过x,y,z都是一次项，我就猜选A吧！

师：通过图形特殊化用空间向量处理，得出一个我们暂时没有学过的方程，生4猜的答案是正确的.

(学生惊呼、赞叹！)

师：但是，说服力稍欠.仔细观察AE,BF这2条异面直线，大家回忆下，通常我们如何处理异面直线间的位置关系？

生：平移.

师：对！经过平移，把空间问题转化成平面问题.

具体解法有2种：

解法1 如图4，取AB的中点M，作EG平行于AB交BC于点G，联结FG，取GF中点N，则四边形OMBN为平行四边形，从而MO∥BN.作CH∥GF交BP于点H，取CH的中点K，因为AE=2BF，所以BG=2BF，而∠CBP是确定的角，于是△BGF∽△BCH，因此点N在BK上，故O在平行于直线BK的一条直线上.

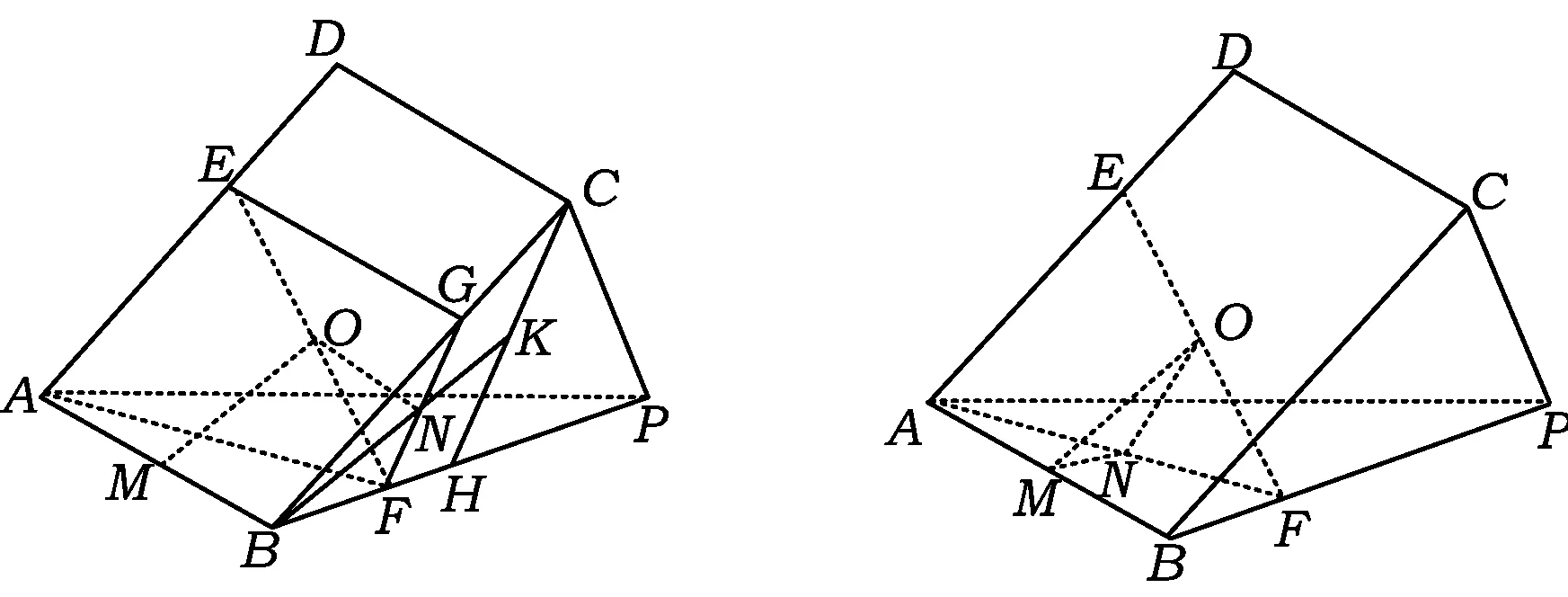
图4 图5

解法2 如图5，取AB的中点M，AF的中点N，联结OM,ON,MN,从而MN∥BF，NO∥AE,且满足NO=2MN.又因为点M的位置确定，且MN始终平行BP，且∠MNO是确定的角.根据三角形相似可知，点O的轨迹是一条直线.

4 若干反思

本文所提的解决立体几何中的轨迹问题，在高考中屡有涉及，且作为选择题的压轴题，难度颇大.但此类问题既然是以立体几何为载体和背景，又以求轨迹为目标，其解题的基本思路也就可以从几何性质和解析几何方法着手，这也是解决此类问题的通性通法.

一方面，指向解题目标，以空间向量法实现形至数的转化.在本文的例1和例4中都体现了这样的思路.学生在使用空间向量法时常会遇到的一个困难是“如何合理地建系”，这是在教学中需要给予关注的.考虑本课是在期末考试中一道得分率不高的选择题基础上设计的一节习题课，学生真实的解题思维并不能通过所选择的最终答案得以揭示，因此在本课的教学中，笔者强调通过与学生间的对话呈现他们真实的思维过程.更重要的是，通过这样的对话让学生感受到建系方式的多样性与选择方法.如在例1中，生1和生2都是通过向量方法解决问题，但与他们的对话中展现给全班学生的是：不同的建系方式导致后续运算、判断等环节难度的差异.另外，考虑到此类问题常以选择题的形式出现，因此特殊化就显得极为重要.特别是在一般情况下建系较为困难时，需要考虑空间向量的特殊化.如例1中设点和直线的特殊化，例4中设几何体形状特殊化、出现的特殊化向量等.

另一方面，尽管此类问题看似是解析几何问题，但几何性质在解题过程中仍起到举足轻重的作用，解题也可以从条件出发挖掘其中蕴含的几何性质，并利用解析几何中常见曲线的定义进行判断.如例2、例3及其变式、例4的解法2都是使用了该思路.

总之，学生解决具有知识交叉综合的数学问题不仅仅是一种挑战，更有助于其自身知识的不断整合与深化，也有助于其数学问题解决能力的提升.因此，知识交叉综合的数学问题是有价值的，未来也许会越来越多见.在教学中，教师要有意识地引导学生去解决此类问题，特别是要教给学生一些通性通法.