一道一元二次方程根的分布题的探索、变式及推广

●杨 虎 (礼县职业中等专业学校 甘肃礼县 742200)

一道一元二次方程根的分布题的探索、变式及推广

●杨 虎 (礼县职业中等专业学校 甘肃礼县 742200)

一元二次方程与一元二次函数、一元二次不等式在中学数学教学中占有重要地位，特别是一元二次方程根的分布问题，更突显方程与函数、不等式之间的紧密联系.虽然这部分知识在高考中的考查有降低要求的趋势，直接考查更是不多，但从培养学生的数学思维能力、数学素养方面来说，引导学生通过对一元二次方程根的分布问题的深入思考，进一步巩固一元二次方程的相关知识，加强对函数及不等式学习的理解，体会数形结合思想方法的重要性有很大的帮助.下面对一道一元二次方程根的分布问题进行探索，对其变式进行探究并加以推广，从而归纳总结一元二次方程根的分布问题的类型及解题规律，以达到触类旁通之效.

1 问题的思考及探索

题目 已知一元二次方程x2+(m+2)x+3+m=0的2个根都小于3，求参数m的取值范围.

错误解法 设方程的2个根分别为x1,x2，根据题意

即

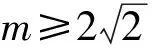
思考 学生在此解法中，由于对题目没有作深入的分析，对已知条件x1<3，x2<3运用不当，想当然而为之，误认为x1<3,x2<3，便可以得到x1+x2<6.在这里x1<3,x2<3是x1+x2<6的充分条件而不是充要条件，因此出现了以上错误的解法，那么此题应如何正确解答呢？

探索1 运用求根公式，直接求解

解法1 设方程的2个根分别为x1,x2，由求根公式得

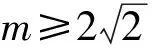
“直接”也就是用平时常用的、最容易想到的方法解题.由于本题是一元二次方程根的问题，自然想到用求根公式，在上面的探索中我们体会到，此解法思维过程简捷，列式简单，但是运算较复杂，特别是对无理不等式的处理，需要学生有扎实的基本功.此时我们不禁发问：能否把问题转化，使其简单一点呢？

探索2 运用转化思想，韦达定理求解

遇到一元二次方程问题，我们自然会想到韦达定理，那么此题运用韦达定理解决能否将问题简化呢？我们不妨一试.

解法2 设方程的2个根分别为x1,x2，由韦达定理知

x1+x2=-(m+2)，x1x2=3+m,

要使方程的2个根都小于3，则需Δ=(m+2)2-4(3+m)≥0且x1<3,x2<3，可等价转化为

即

得

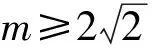
很显然上述探索将问题巧妙地转化后再用韦达定理，达到了简化问题的效果.那么此题是否还有更简单的方法呢？

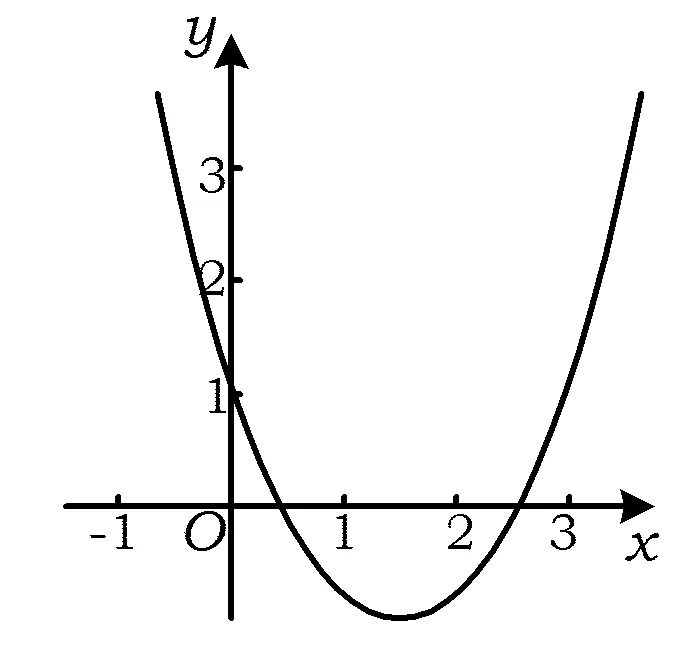
图1

探索3 运用数形结合思想，根据函数图像求解

如图1，一元二次方程的2个根都小于3，也就是一元二次函数与x轴的2个交点都在3的左边，故此题也可用数形结合思想(利用一元二次函数的图像)来求解，即通过对函数f(x)=x2+(m+2)x+3+m的开口方向、对称轴、判别式、特殊点等方面的考查来解决(有时某个方面可以省略，如判别式、对称轴等).

解法3 设一元二次方程为x2+(m+2)x+3+m=0,所对应的二次函数为

f(x)=x2+(m+2)x+3+m,

二次项系数a=1，函数图像开口向上.要使得方程x2+(m+2)x+3+m=0的2个根都小于3，也就是一元二次函数x2+(m+2)x+3+m=0与x轴的2个交点都在3的左边，则需

得

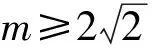
至此，我们发现在以上的3种探索方法中，探索3运用数形结合思想、根据函数图像求解，思维过程最为简捷，运算最为简单，故不失为此题最精妙的解法.不难概括其基本思路是：设出一元二次方程对应的一元二次函数，结合函数图像的特征，对方程的判别式、给定定义域上的函数值、对称轴在定义域上的分布情况进行全面分析，再列出合适的不等式求解.那么这样的思维方法是否也适用于其他同类问题呢？

2 变式探究

变式探究1 若一元二次方程x2+(m+2)x+3+m=0的2个根都大于3，求参数m的取值范围.

变式探究2 若一元二次方程x2+(m+2)x+3+m=0的一根大于3，另一根小于3，求参数m的取值范围.

变式探究3 若一元二次方程x2+(m+2)x+3+m=0的2个根都在[3,4]外，且一根比3小，另一根比4大，求参数m的取值范围.

探究过程 由以上探索3的基本思路，设一元二次方程x2+(m+2)x+3+m=0对应的二次函数为f(x)=x2+(m+2)x+3+m，根据函数图像特征有:

1)如图2,要使一元二次方程x2+(m+2)x+3+m=0的2个根都大于3，也就是一元二次函数f(x) =x2+(m+2)x+3+m与x轴的交点都在3的右边，则需

得

解得m的值不存在.

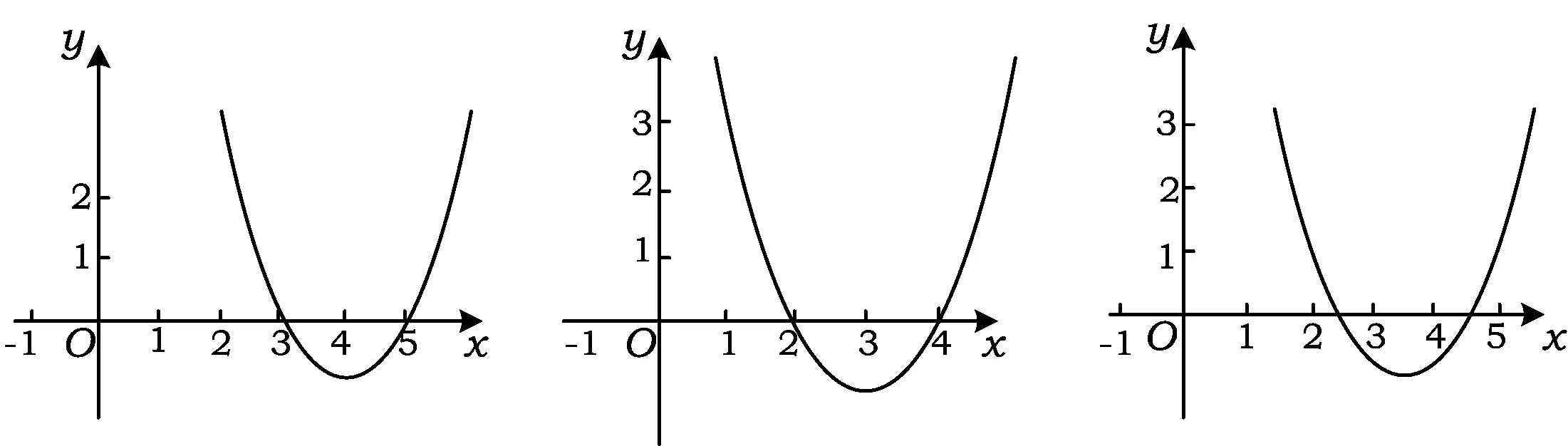
图2 图3 图4

2)如图3,要使一元二次方程x2+(m+2)x+3+m=0的一根大于3，另一根小于3，只需f(3)<0，即

9+3(m+2)+3+m<0,

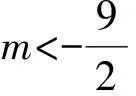
3)如图4,要使一元二次方程x2+(m+2)x+3+m=0的2个根都在[3,4]外，且一根比3小，另一根比4大，则需

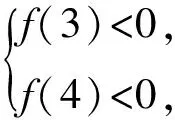
即

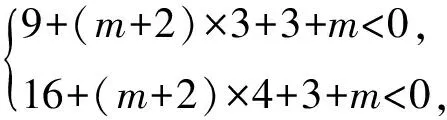
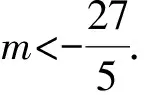
在对以上变式的探索中我们发现，设出一元二次方程对应的一元二次函数，结合函数图像的特征，对方程的判别式、给定定义域上的函数值、对称轴在定义域上的分布情况(有时某个方面可以省略，如判别式、对称轴等)进行全面分析，再列出合适的不等式求解，这种解题思路及基本方法具有一般性，完全适用于其他一元二次方程根的分布问题.

3 推广

基于以上的探索思考、探究归纳，对一元二次方程根的分布类型及解题规律进行推广如下：

对一元二次方程ax2+bx+c=0(其中a≠0)和二次函数f(x)=ax2+bx+c=0，有：

推广1 方程f(x)=0的2个根都比k小的充要条件是

推广2 方程f(x)=0的2个根都比k大的充要条件是

推广3 方程f(x)=0的一根都在(m,n)内，另一根在(p,q)内的充要条件是

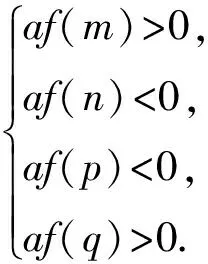
推广4 方程f(x)=0的2个根都在[m,n]内的充要条件是

推广5 方程f(x)=0的一根比k大，一根比k小的充要条件是af(k)<0.

推广6 方程f(x)=0的2个根都在[m,n]外，且一根比m小，另一根比n大的充要条件是

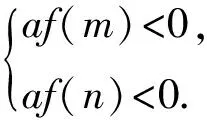
结束语 一元二次方程、一元二次不等式的许多问题常常要借助于与之对应的一元二次函数图像的性质，利用数形结合思想探求解题方法，同时也有不少二次函数问题的解决又常与对应的一元二次方程的根及一元二次不等式的解集密切相关.因此，熟练掌握“3个二次”的内在联系与相互转化，借助函数的图像，是解决诸如此类问题的最佳思路.

[1] 康士凯．新课标高中数学解题思维方法[M].上海:上海科学普及出版社，2007：94-97．

[2] 钟山．高中数学解题方法技巧规律大全[M].北京:现代教育出版社,2007:59-61．

[3] 薛金星.怎样解题(高中数学)[M].北京:北京知识出版社,2007:13-16．

[4] 任勇．高中数学高效学习法[M].北京:人民日报出版社,2001：20-23．

[5] 李永新，李德禄.高中数学教材教法[M].长春:东北师范大学出版社,2000：38-40．