纳米压痕法表征BNT薄膜的压电性能

廖艳果, 胡和平，*， 郑学军

(1.南华大学 数理学院,湖南 衡阳 421001；2.湘潭大学 低维材料及其应用教育部重点实验室,湖南 湘潭 411105 )



纳米压痕法表征BNT薄膜的压电性能

廖艳果1, 胡和平1，2*， 郑学军2

(1.南华大学 数理学院,湖南 衡阳 421001；2.湘潭大学 低维材料及其应用教育部重点实验室,湖南 湘潭 411105 )

利用有限元方法模拟了BNT薄膜/基底体系的纳米压痕过程，分析讨论了BNT薄膜的压电参数对加载的最大压痕载荷、加载曲线指数的影响，用量纲分析结合有限元方法建立了压痕的加载参数和BNT薄膜的压电参数的无量纲关系.

有限元方法；加载曲线；压电参数；无量纲关系

BNT薄膜(即铁电薄膜)因具有独特的压电性、铁电性、介电性、热释电性以及非线性光学等性能，在铁电存储器、红外探测器、集成光电器件、空间光调制器、光学传感器等方面有着极其广泛的应用前景，正朝着实用化发展.BNT薄膜的制备、结构及性能的研究受到广泛的关注.BNT薄膜所具有的压电性能对其应用具有重要的意义，准确测量其压电参数十分重要[1]，目前国内对薄膜压电性能的测量方法很少，怎样表征其压电性能成为一项重要任务.绝大多数的薄膜都束缚于基底材料之上，这样给其压电性能的表征带来了困难，体现在以下几个方面：(1) 从基底上剥离出薄膜比较困难，剥离的薄膜一般非常薄，为微纳米级，对如此薄的试样样品进行压电性能测试容易发生破坏和损伤，这样就会对测试所得的实验结果产生较大的影响；(2) 如果直接对薄膜/基底体系进行压电性能测量，则测量出的结果往往受到基底性能的影响，而与薄膜的真实压电性能有差异.因此我们需要发展新的方法来表征薄膜材料的压电性能.

目前，测量薄膜压电性能的方法主要分为直接测量法和间接测量法.直接测量法主要有气腔压力法、悬臂梁法、激光干涉法、激光多普勒振动法等，间接测量法有传统阻抗分析法等.随着现代测试技术的发展，人们通过微纳米压入法来研究薄膜材料的力学、压电等性能[2].微纳米压痕法可以在不分离薄膜和基底的情况下，测量出薄膜的力学、压电等性能，该方法对样品尺寸要求小，精确性高，成为一种表征薄膜材料力学、压电性能的常用方法.本文运用量纲分析并结合有限元方法建立了纳米压痕的加载曲线参数和BNT薄膜的压电参数之间无量纲关系，为表征BNT薄膜的压电性能提供了一种新的方法.

1 量纲分析

BNT薄膜材料的力学本构关系可表示如下[3]：

εij=sijklσkl，

(1)

其中σkl为应力分量，εij为应变分量，sijkl为材料的弹性常数.BNT薄膜材料为横观各向同性材料，(1)式中的应力应变关系又可表示为：

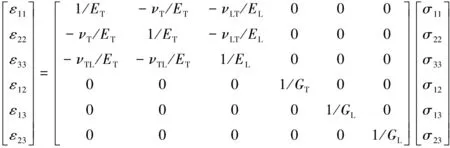
(2)

式中，EL为纵向弹性模量，ET为横向弹性模量，GL为纵向剪切模量，GT为横向剪切模量，νTL，νLT和νT是材料的泊松比.这7个力学参数并不是独立的，其中，横向剪切模量GL和横向弹性模量ET与泊松比νT关系如下：

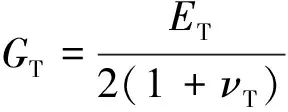
(3)

而横向和纵向弹性模量与泊松比之间满足如下关系：

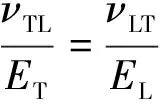
(4)

这样，独立的弹性常数就只有5个，为ET，EL，GL，νTL和νT.根据研究，各向异性材料的压痕模量为各个不同方向杨氏模量的加权平均，对于横观各向同性材料，其压痕模量近似为不同方向弹性模量的平均值[4～6]，即

Em=(ET+EL)/2， (5)

式中Em为纳米压痕实验测定的压痕模量.

图1是一个典型的锥形压痕的加卸载曲线，图中，Fmax为最大载荷，hm为压入的最大深度.可用如下幂指数函数来拟合加载部分，即Fm=chx.

纳米压痕过程中Fmax和x应是薄膜和基底的力学参数(s11,s13,s33,s55,s66,ES,νs)以及薄膜厚度(t)、最大压痕深度(hm)、介电常数(κ33)、压头半角(θ)和压电参数(e15,e31,e33)的函数.因此，Fmax和指数x应该是以上这些参数的函数，即

(6a)

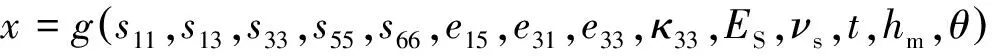
(6b)

本文中采用θ=70.3°的Berkovich金刚石压头，如果薄膜的弹性常数即sij已知，介电常数κ33可通过选用块体材料的值或者查文献近似表示，νs可近似地取为0.3[7～9]，则公式(6)可简化为：

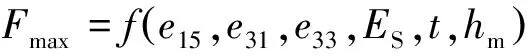
(7a)

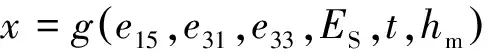
(7b)

取ES、hm与e33作为基本参量，并应用∏定理，可得

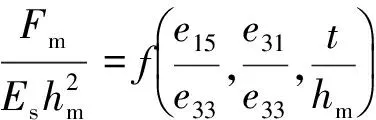
(8a)

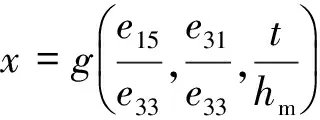
(8b)

在这里，固定t/hm为5，方程(8)可进一步简化为

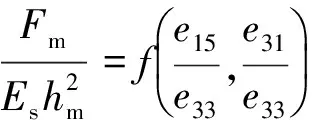
(9a)

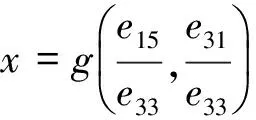
(9b)

2 有限元数值模拟

本文使用有限元软件 ABAQUS 对纳米压痕过程进行数值模拟, 总的来说，为了简化问题，模拟压痕过程中，假设Berkovich 金刚石压头为刚性压头，薄膜和基底之间为完美结合，压头和薄膜之间的摩擦为库仑摩擦，摩擦系数为0.1.根据投影面积与压入深度的比值, 将 Berkovich 压头等效成 70.3°的圆锥形压头[7～9], 因为试样和压入过程具有轴对称性, 可将三维的问题简化成二维的轴对称问题.我们在其压入过程的有限元网格划分中：被压材料靠近压头部位的网格较密, 靠边缘部位的网格比较稀, 在模拟过程中用了8 055个四节点轴对称线性减缩积分单元 (CAX4R) 的网格单元，其压入过程的有限元网格划分如图2所示.

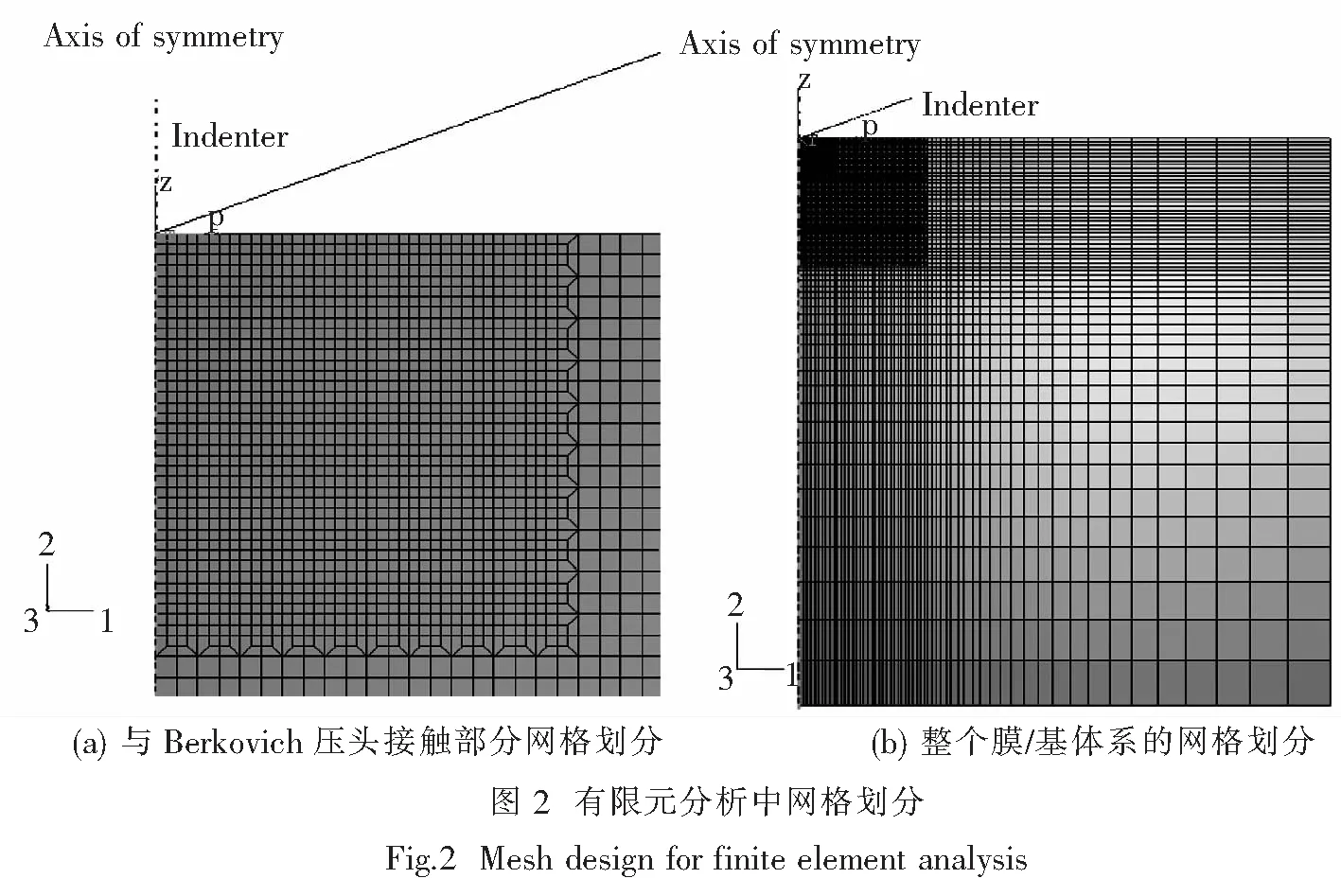
表1 BNT与Si基底热物理参数

Tab.1 The thermal physical parameters of BNT and Si substrate

密度/(103kg·m-3)比热/(J·kg-1·℃-1)导热率/(W·m-1·℃-1)热扩散系数/(m2·s-1)热膨胀系数/(10-6K-1)BNT8．4362102．041．17×10-615Si2．47031508．89×10-52．5

在用有限元分析软件模拟BNT薄膜/基底体系纳米压痕过程中，通过改变其压电系数的值，就可以得到不同压电系数组合下的加载曲线.然后通过拟合数值模拟中无量纲化的加载参数与压电系数的关系，即方程(9)，就可以得到具体的无量纲方程表达式.我们选用沉积在Si基底上的BNT薄膜的膜厚为1 μm，数值模拟计算中要用到的BNT薄膜和Si基底材料的热物理参数如表1所示.

3 数值计算结果和讨论

通过大量的有限元模拟，我们可以得到加载曲线指数x、无量纲化的最大加载力Fmax/EShm2与无量纲化压电系数之间的关系曲线，如图3所示.

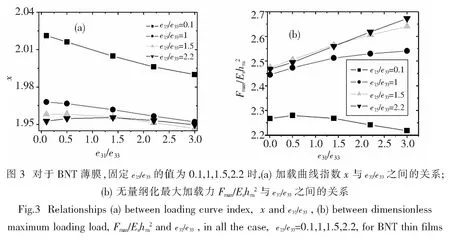
通过Origin软件拟合图3的关系，方程(9)的具体形式如下：

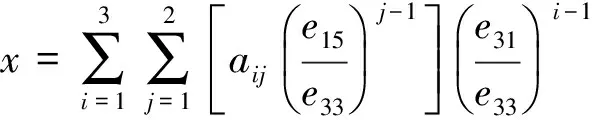
(10a)

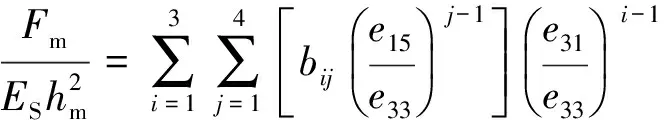
(10b)

方程(10)中的拟合系数aij和bij列于表2.

表2 方程10中拟合的系数

在无量纲方程(10)中，有未知压电参数e31，e33和e15，要求得这三个压电参数，首先需要确定基底的弹性模量和薄膜材料的力学参数，另外还需要通过纳米压痕实验得到BNT薄膜材料的压痕模量Em，最后通过纳米压痕实验得到加载-位移曲线，从曲线中得到最大加载荷载Fmax和幂指数x.

应变压电系数d33也是表征压电材料压电性能的一个参数，它和压电系数eij有如下的关系[11]：

d33=2e31s13+e33s33,

(11)

其中，弹性常数sij是已知的，只要知道了d33的值，就可以建立一个关于压电系数eij的方程.利用方程(10)和(11)，就可求得三个压电参数e31，e33和e15，其整个分析过程的流程如图3所示.

4 结 论

应用有限元法模拟了横观各向同性BNT薄膜的纳米压痕过程，并结合无量纲方法建立了加载曲线参数和BNT薄膜的压电系数之间的无量纲关系.提供了一种表征BNT薄膜压电性能的新方法，该方法不需要把薄膜从基底中分离出来，在不破坏试样的情况下即可表征出BNT薄膜的压电参数.该方法为BNT薄膜在现代微电子、微机电系统(MEMS)、信息存储等工程、工艺当中的广泛应用提供了技术支持.但是，在应用该方法时，注意到如果压头压入很浅时，需要考虑尺度效应，因此只有在压入不太浅时，才可用该模型来表征BNT薄膜的压电参数.

[1] YANG Y T, LIAO J D, LEE Y L,et al. Ultra-thin phospholipid layers physically adsorbed upon glass characterized by nano-indentation at the surface contact level[J]. Nanotechnology，2010, 6(14):195 702.

[2] 廖艳果, 胡和平, 王晓锋. 压痕法表征韧性膜力学性能的量纲分析[J]. 材料研究与应用，2013, 7(4)：235-237.

[3] SAHA R, NIX W D. Effects of the substrate on the determination of thin film mechanical properties by nanoindentation[J]. Acta Materialia， 2002,50(1):23-38.

[4] VLASSAK J, CIAVARELLA M, BARBER J,et al. The indentation modulus of elastically anisotropic materials for indenters of arbitrary shape[J].Journal of the Mechanics and Physics of Solids， 2003(51):1 701-1 721.

[5] WANG J S, ZHENG X J, ZHENG H,et al. Identification of elastic parameters of transversely isotropic thin films by combining nanoindentation and FEM analysis[J].Computational Materials Science，2010, 49(2):378-385.

[6] TAO Y W, ZHENG X J, LIU W,et al. Determination of the mechanica lconstants of ZnS nanobelt by combining Nanoindentation test and finite element method[J].International Journal of Solid sand Structures, 2013,50:487-497.

[7] 廖艳果, 胡和平, 周益春.加工硬化对薄膜基底体系临界压痕极限的影响 [J]. 湘潭大学自然科学学报, 2011, 33(2):17-21.

[8] 廖艳果, 胡和平, 周益春. 能量法表征硅基底上韧性薄膜的塑性性能 [J]. 材料研究与应用，2010，4(1)：44-47.

[9] 廖艳果, 蒋丽梅, 胡和平，等. 韧性薄膜/韧性基底体系弹性模量表征的新方法(英) [J]. 湘潭大学自然科学学报, 2013, 35(2):20-25.

[10] LIAO Y G, ZHOU Y C, HUANG Y L,et al. Measuring elastic-plastic properties of thin films on elastic-plastic substrates by sharp indentation [J]. Mech Mat, 2009, 41(3): 308-318.

[11] DAMJANOVIC D. Ferroelectric, dielectric and piezoelectric properties of ferroelectric thin films and ceramics [J]. Rep Prog Phys, 1998, 9(61):1 267-1 324.

责任编辑：罗 联

Identification of Piezoelectric Properties of BNT Thin Films by Nanoindentation Method

LIAOYan-guo1,HUHe-ping1,2*,ZHENGXue-jun2

(1.School of Mathematics and Physics, University of South China, Hengyang 421001；2.Key Laboratory of Low Dimensional Materials and Application Technology of Ministry of Education,Xiangtan University, Xiangtan 411105 China)

In this paper, the finite element method (FEM) has been employed to study the nanoindentation experiment of BNT thin film/substrate systems. The influences of the piezoelectric properties of BNT thin films on the maximum indentation load and loading curve index have been analyzed. Using dimensional analysis and finite element computation method, the corresponding dimensionless relationship between the loading parameters and piezoelectric properties of BNT thin films has been obtained.

finite element method (FEM)； loading curve； piezoelectric properties； dimensionless relationship

2015-03-24

湖南省科技厅项目 (2012GK3136) ; 湖南省衡阳市科技局项目 (2011KJ75)

胡和平(1964— ),男，湖南 衡阳人，副教授. E-mail:liaoo@qq.com

TN384

A

1000-5900(2015)03-0009-06