大口径平面面形绝对测量及重力影响分析
2015-05-03王艳茹冉铮惠
徐 德,王艳茹,冉铮惠
(中国工程物理研究院计量测试中心,四川 绵阳 621000)
0 引 言
数字波面干涉测量技术将光学干涉和数字计算技术相结合,可以实现高精度、快速、非接触式和自动化测量,在惯性约束聚变(ICF)、空间遥感探测以及极紫外光刻(EUVL)等大型超精密光学系统工程中应用广泛[1-4]。激光平面干涉测量结果的准确性受参考平面面形精度的制约,为了得到平面光学元件绝对面形偏差,研究人员提出了多种解决方案,其中最常用且较容易实现的是G.Schulz和J.Schwider[5-6]提出的三平面互检法。但该方法只能得到3个平面沿着轴线方向的面形偏差。Bernard S.Fritz[7]对该方法进行了改进,通过增加一次旋转测量,并利用Zernike多项式作为基函数进行最小二乘法拟合,得到全面形偏差。Chiayu Ai和James C.Wyant[8-9]在三平面互检算法方面开展了大量研究,提出利用奇偶函数法进行任意平面全面形绝对测量的算法理论,该方法不需要进行波面拟合,算法更加简单,且计算速度更快。
影响三平面互检结果准确性的另一个重要因素是镜片自身重力引起的面形变化[10],而目前这方面的研究较少。本文通过有限元分析的方法对镜片在不同夹持方式下的面形变化进行了仿真分析,基于仿真分析结果对三平面互检数据进行修正,最终得到3个平面的绝对面形偏差。
1 奇偶函数算法的基本原理
假设 A、B、C 3 个面的面形分别用 FA(x,y),FB(x,y),FC(x,y)表示,通过数学推导可知,对于任意非对称二维函数 F(x,y),有:

其中:
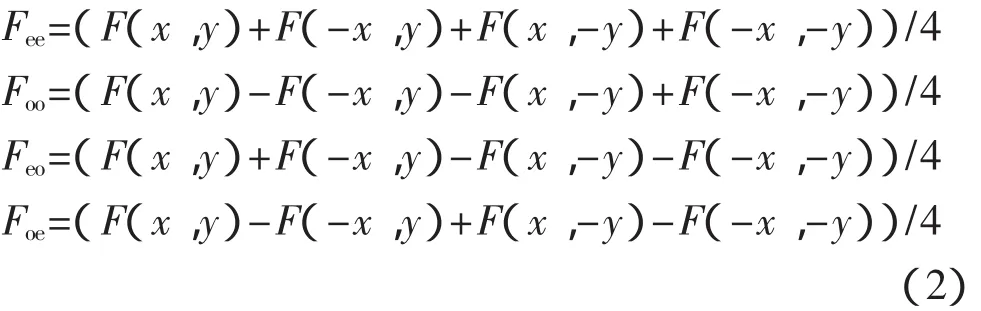
Fee、Foo、Feo、Foe分别代表 F(x,y)中的偶-偶、奇-奇、偶-奇、奇-偶分量。所以任意非对称函数F(x,y)都可表示为上述4个分量之和。根据该原理,进行图1所示的8种组合干涉测量,即可实现上述4个分量的测量,从而得到全口径面形F(x,y)。

图1 基于8组干涉测量的三平面互检校准原理图
8组干涉测量所对应的数学表达式为

其中,上标x表示绕y轴翻转,上标角度θ表示逆时针旋转θ角度。首先求出Aoe+Aeo,Boe+Beo,Coe+Ceo分量:
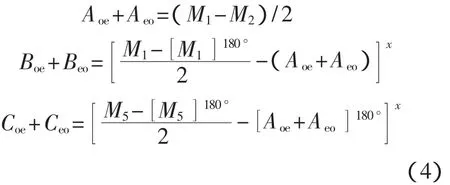
设:

Aee、Bee、Cee3 个分量可由下式求出:

定义 A′、B′、C′为以上 3 个分量之和,即:

对于3个面的奇-奇分量,不能由前面表达式直接得到。分析可知,分布在同一圆周上的所有点所对应的函数若在直角坐标系中为奇-奇函数,则将其转化到极坐标中后应为关于角变量θ的奇函数,且函数周期为180°。因此,可将一奇-奇函数Foo(x,y)表示为下式所示的傅里叶正弦级数的形式:

通过进一步的变换推导可求 Aoo、Boo、Coo,对于平滑表面,取级数前两项即可。
先求取级数,第1项:

设:

可求得级数第2项为

最终全面形表达式为
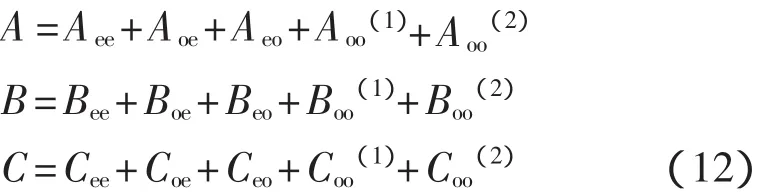
2 重力变形的仿真分析
在进行三平面互检绝对测量过程中,需要将其中两片平面镜进行多个角度的旋转,在保证环境条件满足测量要求的前提下,镜片自身重力导致的镜片形变将会对测量结果产生影响。为获取大口径光学元件因自重所引入的面形分量大小以及面形分布情况,针对不同的夹持方式(三爪工装夹持、圆弧工装夹持及180°柔性吊带工装夹持),采用ANSYS有限元分析软件对大口径光学元件面形分布进行了仿真计算。
有限元分析参数设置如下:镜片尺寸φ320mm×60mm,材料为石英玻璃,杨氏模量69GPa,泊松比为0.208,密度 2120 kg/m3,热导率 1.7W/mK,热膨胀系数5.5×10-7K-1,网格尺寸10mm,单元类型为solid45。
对于三爪工装,实际只有下方两个支撑点对镜片产生应力,上方的支撑点仅对镜片起保护作用,图中x和z坐标轴在镜片平面内,y轴沿镜片法线方向。因此,对下方两个支撑点处沿x和z方向的位移约束为0。图2为三爪工装夹持的仿真结果,其表面变形的PV值为5.6nm。

图2 三爪工装夹持的受力变形仿真结果(单位:m)
为了改进局部应力集中的问题,在三爪工装的基础上设计了不同几何参数的圆弧式工装夹具,即将线接触改为与镜片侧面曲率相同的圆弧式面接触夹持方式,并通过增加柔性材料以增大其接触面。同样利用有限元法仿真计算不同接触面积的圆弧工装对镜片产生的应力,约束条件与图2中类似,即镜片侧面与圆弧支撑面接触处沿x和z方向位移为0。图3为圆弧张角为15°和30°的仿真计算结果,相应的面形变化的PV值分别为2.7,1.84nm。由此可见,随着支撑圆弧的面积增大,所产生的面形变化量也随之减小。
此外,还对180°柔性吊带工装夹持情况下的镜片表面面形变化进行了仿真分析,使镜片侧面与吊带支撑面接触处沿x和z方向位移为0,仿真计算结果如图4所示,其表面变形的PV值仅为0.41nm。
由上述仿真结果可知,与三爪工装和圆弧工装相比,采用柔性吊带工装进行夹持时,镜片沿法线方向的形变量大大减小,这是因为柔性吊带工装与镜片侧面的接触面增大,对局部应力进行匀化的结果。因此在实际测试中,对于大口径光学元件垂直放置时,为了减小光学元件因自身重力所引入的面形误差,推荐采用柔性吊带支撑这种装夹方式。
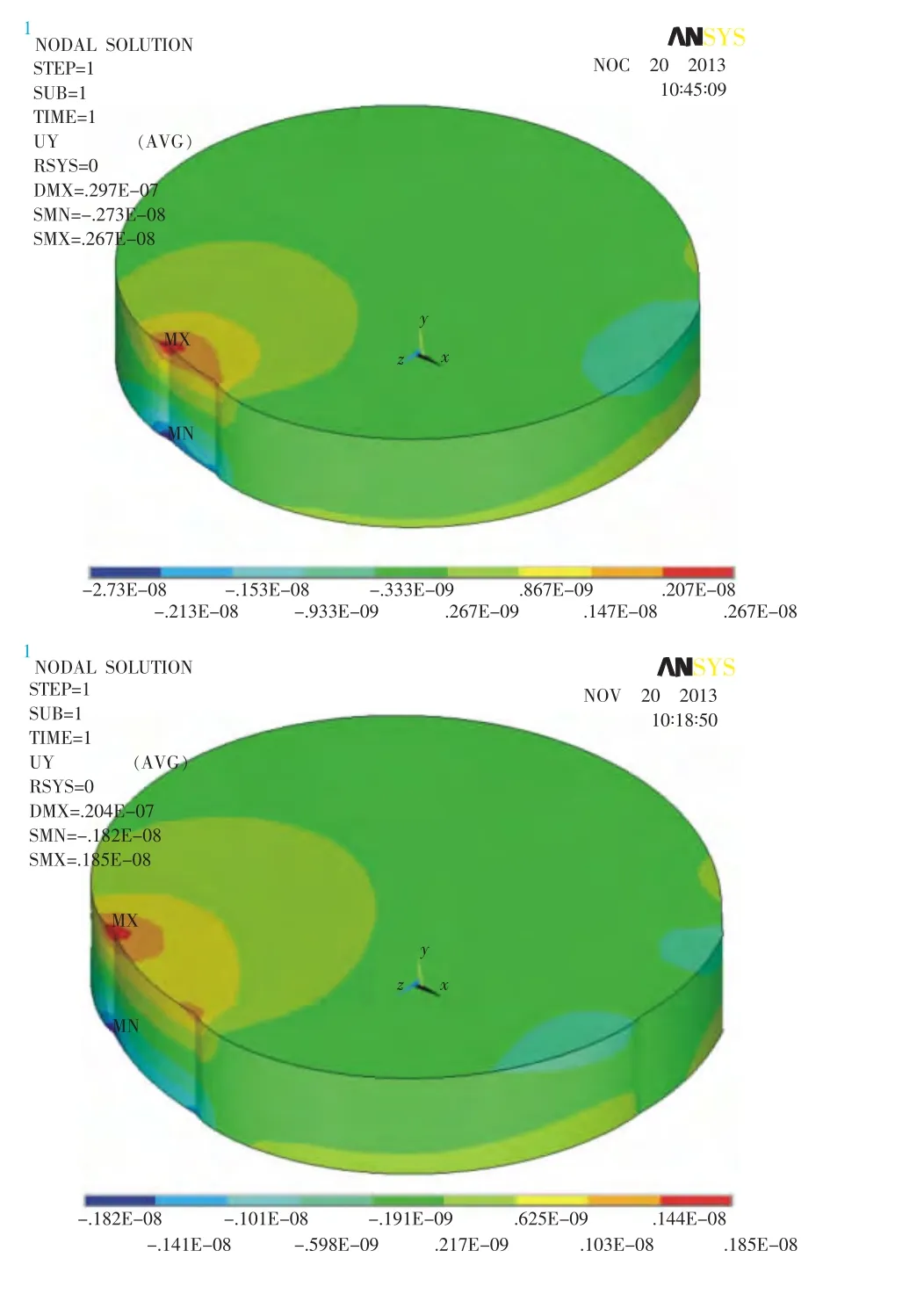
图3 张角分别为15°和30°圆弧工装夹持的受力变形结果(单位:m)

图4 柔性吊带工装夹持的受力变形仿真结果(单位:m)
3 实验测量与数据处理
按照公式所表示的8种组合进行测量,每种组合测量5组×10次=50次,剔除测量结果中受到振动和空气扰动影响的数据,取有效测量结果的均值,作为每种组合的测量结果,进一步计算处理,测量结果如表1所示。

表1 三平面互检8组干涉测量结果1)
根据奇偶函数法的数学模型,编写三平面互检的数据处理程序,可得到最终A、B、C 3个平面的绝对面形信息。上述测量结果中包含旋转角度误差和横向平移误差,国外有研究机构采用昂贵的精密八维调整架和特殊的中心对准方法来解决该问题。本文利用图像处理的方法,基于最小二乘法建立数学模型,通过优化分析得到两次测量之间的旋转角度偏差及平移误差,并对测量结果进行补偿。在不考虑镜片应力变形的情况下,最终测量结果如图5所示。
通过计算得到,3个面的绝对面形数据分别为
A 面:PV_A=0.1041λ,rms_A=0.0194λ
B 面:PV_B=0.1010λ,rms_B=0.0136λ
C 面:PV_C=0.1282λ,rms_C=0.0195λ
若考虑应力变形,需将实验测得的8组数据扣除应力变形量之后再进行计算。由于柔性吊带工装所产生的应力变形量最小,因此,仅对该情况进行分析。利用编写的程序计算得到的面形分布情况如图6所示。

图5 未进行应力变形补偿的A、B、C 3个平面面形的绝对测量结果
此时3个面的绝对面形数据分别为

图6 应力变形补偿后A、B、C 3个面的绝对面形
A 面:PV_A=0.1038λ,rms_A=0.0194λ
B 面:PV_B=0.1009λ,rms_B=0.0136λ
C 面:PV_C=0.1281λ,rms_C=0.0195λ
由图6可知,3个平面的面形偏差基本为环状分布,这与8组干涉测量中的每次测量结果有区别。由于3片平面镜的加工是利用环形抛光工艺完成的;因此,面形偏差按照环状分布与最终测量的分布情况相吻合。此外,将图5中未进行应力变形补偿的结果与图6进行对比后可知,采用柔性吊带支撑时,3个镜片在应力变形补偿前后其面形偏差分布基本一致。由于重力和装夹产生的面形变化PV值分别为0.0003λ,0.0001λ,0.0001λ,而 rms值则基本相同。因此,对于φ300mm口径的石英玻璃镜片而言,采用柔性吊带工装进行夹持所造成的镜片应力变形量非常小,这对于较大口径光学元件的高精度面形检测是很有利的。
4 结束语
本文基于Chiayu Ai和James C.Wyant提出的奇偶函数法三平面互检理论,通过8组干涉测量得到3个待测平面的面形数据。利用有限元分析的方法研究了不同工装夹持方式下镜片因重力所产生的变形情况,并基于有限元仿真计算结果对三平面互检的数据进行修正和补偿。研究结果表明,对于φ300mm口径的石英玻璃镜片,利用柔性吊带工装支撑时其面形变化量仅为0.0001λ量级,对测量结果的影响几乎可以忽略。
[1]张蓉竹.ICF系统光学元件高精度波前检测技术研究[D].四川:四川大学,2003.
[2]Burge J H,Davison W,Martin H M,et al.Development of surface metrology for the Giant Magellan Telescope primary mirror[C]∥Proc SPIE 7018,Advanced Optical and Mechanical Technologies in Telescopes and Instrumentation,701814,2008.
[3]张宇,金春水,马冬梅,等.极紫外光刻物镜系统波像差检测技术研究[J].红外与激光工程,2012(12):1-8.
[4]Tejnil E,Kenneth A.Goldberg S H L.At-wavelength interferometry for extreme ultraviolet lithography[J].J Vac Sci Technol,1997,15(6):2455-2461.
[5]Schulz G,Schwider J.Precisemeasurement of plainness[J].Appl Opt,1967,6(6):1077-1084.
[6]Schulz G,Schwider J,Hiller C,et al.Establishing an optical flatness standard[J].ApplOpt,1971,10(4):929-934.
[7]Fritz B S.Absolute calibration of an optical flat[J].Opt Eng,1984,23(4):379-383.
[8]Ai C,Wyant J C.Absolute testing of flats decomposed to even and odd functions[C]∥SPIE,1992(1776):73-83.
[9]Ai C,Wyant J C.Absolute testing of flats by using even and odd functions[J].Appl Opt,1993,32(25):4698-4705.
[10]Malacara D.Optical shop testing(3rd edition)[M].New Jersey:John Wiley&sons Inc,1978:40-44.
