短时傅里叶变换声-超声检测信号缺陷识别

艾春安， 蔡笑风，， 刘继方， 王晓明

（1.第二炮兵工程大学动力工程系，陕西 西安 710025；2.第二炮兵工程大学士官学院，山东 青州 262500）

0 引 言

自从1979年NASA Lewis研究中心的A.Vary提出声-超声检测技术并将其成功应用于纤维复合材料的损伤检测后，该检测技术迅速得到广泛应用[1-2]。Aduda[3]等在对声-超声信号进行谱分析时发现，信号频谱呈现出以相同基频为间隔的一系列峰值，认为声-超声信号可用共振波理论解释；法国Boinet、Marlot[4]等利用声-超声技术对金属与电解液界面产生的气体进行实时监测，并对监测信号进行时频分析，得出了流体中动态气泡的变化规律。张训亚[5]利用声-超声技术提取反映木材声波传播效率的一个或多个参数，并与木材主要性质建立关系模型，以实现木材质量的有效预测；张蕾[6]基于声-超声技术对铝板中Lamb波的时频特性进行理论和实验研究，实现了铝板结构损伤监测的定性研究；车飞[7]采用基于短时傅里叶变换的时频分析方法，对薄板中传播的声超声信号进行处理分析，取得了良好效果。

声-超声信号作为一种非平稳信号，含有较多突变分量，其1阶、2阶统计量和功率谱的估计显然不能简单地使用平稳信号的估计方法。因此本文提出将短时傅里叶变换这一典型线性时频分析应用于声-超声检测信号的缺陷识别研究中。

1 短时傅里叶变换

信号 z（t）的短时傅里叶变换（STFT）定义为

式中：*——复数共轭；

g（t）——时间宽度很短的窗函数，沿时间轴滑动。

由于信号乘以一个相当短的窗函数等价于取出信号在分析地点附近的一个切片，所以可以理解为信号在“分析时间”附近的傅里叶变换[8]。

函数 STFT z（t，f）可以看作是信号 z（t）与窗函数 g（u）的时间平移-频率调制形式 gt，f（u）的内积，即：

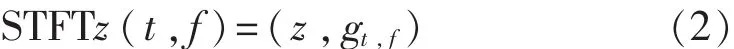
式中

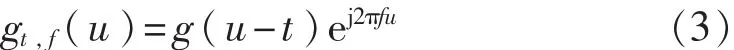
而

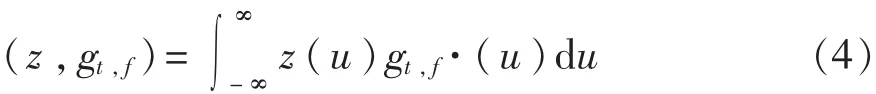
原则上，分析窗函数g（t）可以在平方可积分空间即L2（R）空间内任意选择。不过在实际应用中，选择的窗函数是一个窄的时间函数，以使式（1）的积分仅受 z（t）及其附近的影响。g（t）的宽度越小，则时频分辨率越好，同时局部平稳性的假设越成立；在频域，由于ej2πfu为δ函数，因此仍可保持较好的频域分辨率[9]。

2 检测信号的提取

2.1 声-超声检测系统

声-超声检测基本原理是利用压电换能器在材料表面激发询问应力波，该应力波在材料内部与材料的微结构经过复杂的相互作用，到达置于材料的同一或另一表面的接收装置，通过分析接收到的声-超声信号可确定材料内部性能的变化，进而判断材料内部是否存在缺陷[10]。

2.2 检测对象

试验制作的检测试件为某型火箭发动机壳体粘接结构，由钢壳体/绝热层构成，其中绝热层材料为三元乙丙橡胶，在粘接界面上预制了一个空气夹层脱粘缺陷及两个孔洞缺陷。试件长220mm，宽120mm，钢壳体厚度3mm，绝热层厚度5mm。其实物照片如图1所示。

2.3 检测信号

图1 钢壳体试件实物照片

图2 试件上各位置处时域波形图

试验中选用2.5MHz探头，考虑到探头频率的有效范围和奈奎斯特采样定律，设定采样频率为50MHz，基线为47，采样深度为8K。在试件上无缺陷、脱粘缺陷及孔洞位置处各采集一组数据，平均滤波后的时域波形如图2所示，图示信号中1部分表示始波，2部分表示含试件内部缺陷信息的应力波。

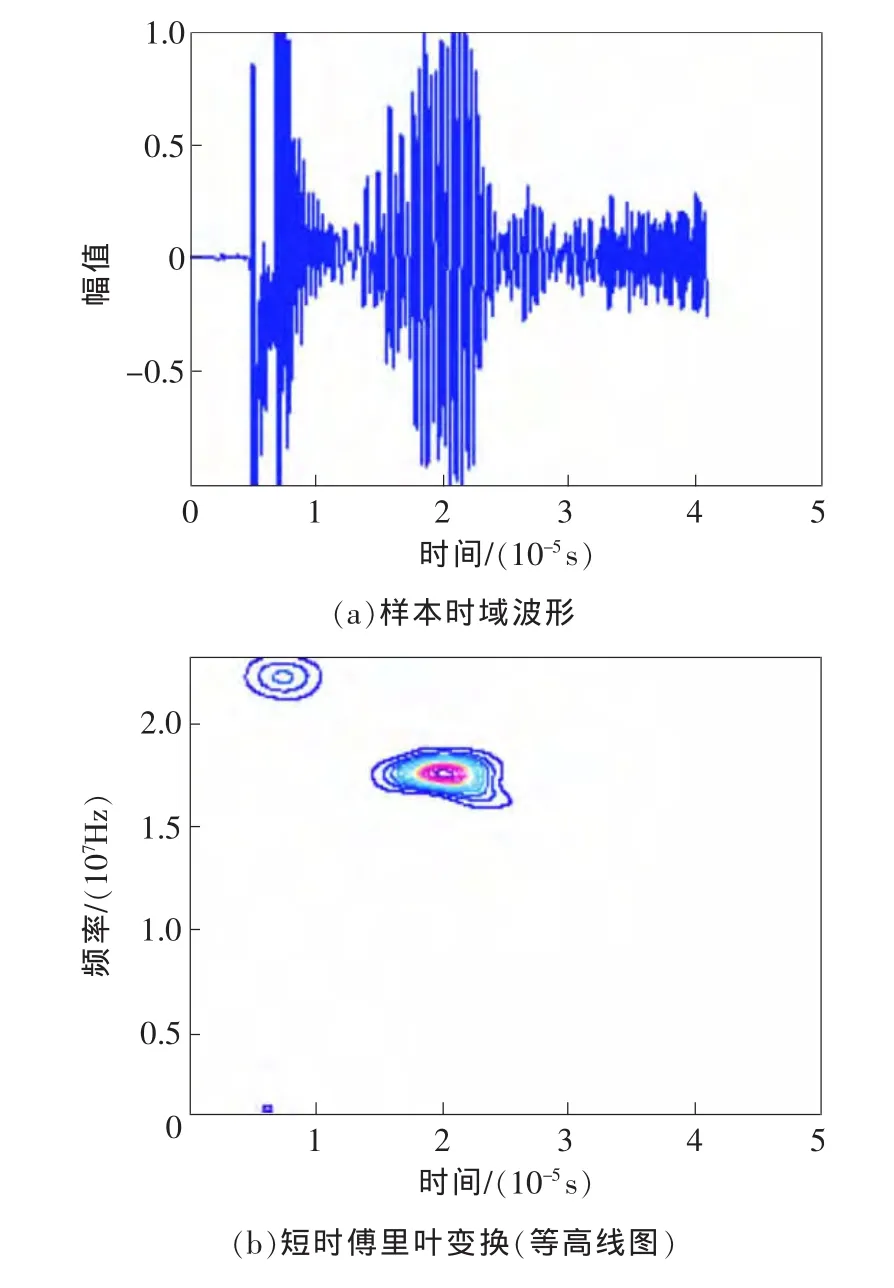
图5 孔洞1信号时频分析

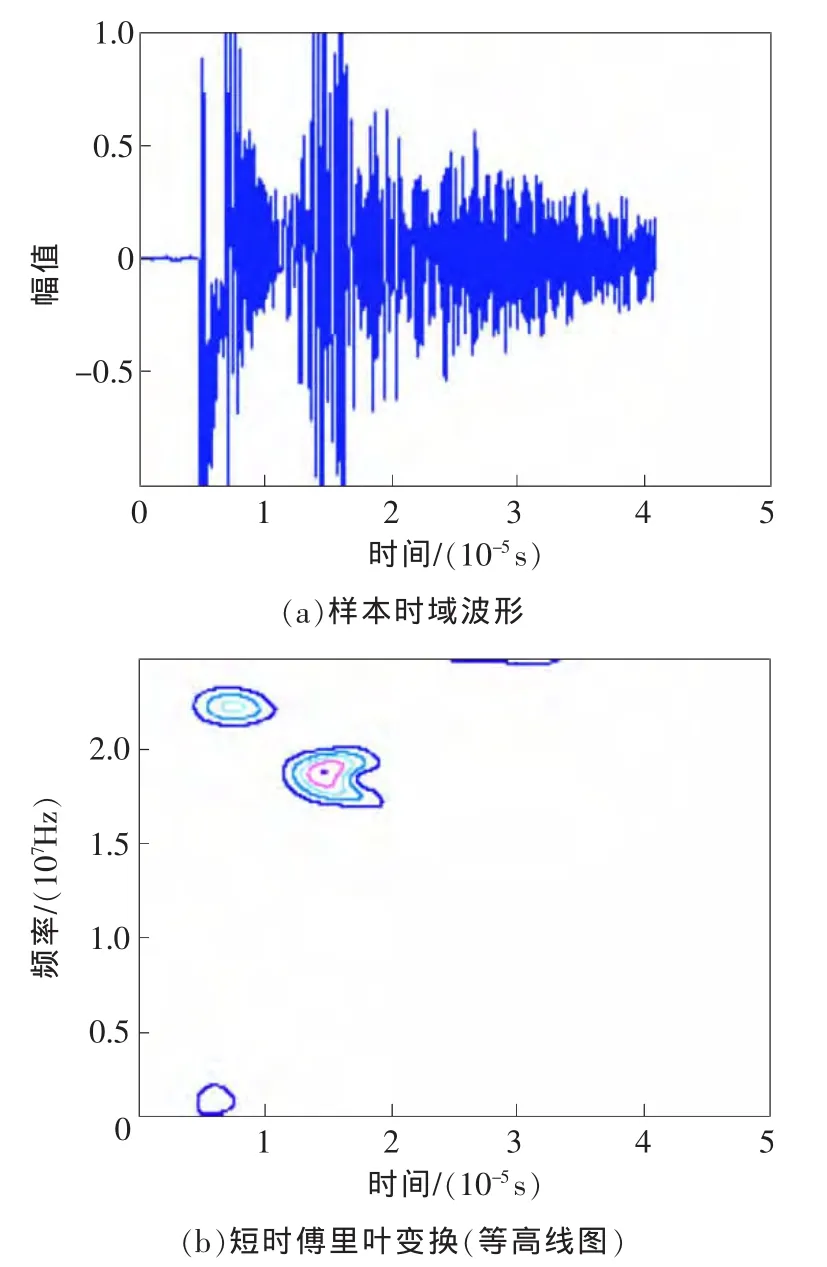
图6 孔洞2信号时频分析

3 检测信号的缺陷识别

取样本长度为2048，选用长度为85的hamming窗对检测信号进行短时傅里叶变换，试件中无缺陷信号、脱粘信号、孔洞1及孔洞2信号的时频分析分别如图3～图6所示。

从图中可以得出：

1）对比4图发现，无缺陷信号相较于有缺陷信号时频面特征较少，主要集中在3～10μs之间，分别以2，22MHz为中心，对比样本时域波形可知，两者分别为始波及其谐波分量。

2）脱粘及两孔洞信号中存在明显的缺陷特征，其中脱粘信号缺陷特征位于20～40μs之间，以15MHz为中心；两孔洞信号缺陷特征均位于10～20μs之间，以18MHz为中心，两者时频特性相近。

3）当选用85点的hamming窗函数进行短时傅里叶变换时，脱粘信号具有相对较好的频率分辨率，而孔洞缺陷具有较好的时间分辨率。

4 结束语

接收到的声-超声信号携带了大量的结构信息，不同结构其时频特性不同，相近结构其时频特性相似。当选用2.5MHz探头，采样频率设为50MHz时，脱粘缺陷信号频段位于15MHz附近，孔洞缺陷信号频段位于18MHz附近，从而通过提取时频特征实现对声-超声检测信号的缺陷识别。

[1]Joseph L，Rose.Ultrasonic waves in solid media[M].1999：23-31.

[2]Tua P S，Quek S T.Detection of cracks in plates using piezoactuated Lamb waves[M].2004（4）：51-60.

[3]Aduda BQ，Rawlings R D.Spectral analysis of acoustoultrasonic waves for defect sizing[J].NDT&E International，1996，94（4）：237-240.

[4]Boinet， Marlot， Lenain.First results from coupled acoustoultrasonics and electro-chemical nosie techniques applied to gas evolving electrodes[J].Electrochemistry Communications，2007，9（9）：2174-2177.

[5]张训亚.兴安落叶松木材性质的声-超声技术预测[D].北京：中国林业科学研究院，2011.

[6]张蕾，杜振宴，武利为.基于小波再分配尺度谱的Lamb波时频特性研究[J].强度与环境，2013，40（3）：31-35.

[7]车飞，彭伟.薄板声-超声检测信号的时频分析研究[J].南昌航空大学学报：自然科学版，2007，21（3）：36-40.

[8]张贤达.现代信号处理[M].北京：清华大学出版社，2002：19-27.

[9]胡广书.数字信号处理[M].北京：清华大学出版社，2003：51-62.

[10]尼涛.SRM复合材料壳体粘接结构声-超声检测方法研究[D].西安：第二炮兵工程学院，2010.