全玻璃真空太阳集热管空晒性能的数值模拟分析*

刘佰红， 高文峰， 刘滔， 林文贤， 邢秀兰， 胡小芳

(云南师范大学 太阳能研究所，教育部可再生能源材料先进技术与制备重点实验室，云南 昆明 650092)



全玻璃真空太阳集热管空晒性能的数值模拟分析*

刘佰红， 高文峰， 刘滔， 林文贤， 邢秀兰， 胡小芳

(云南师范大学 太阳能研究所，教育部可再生能源材料先进技术与制备重点实验室，云南 昆明 650092)

利用FLUENT对Ø58×1 800 mm全玻璃真空管在不同发射率、真空度下空晒热性能进行数值模拟与分析，并通过空晒实验来验证模拟结果的正确性.数值分析结果表明：发射率越低，真空管的热损失越小，真空管的热性能越好.真空管空晒热性能随真空夹层压强的增加而减小，真空管空晒性能变化主要位于10-1～10 Pa范围，当压强小于10-1Pa或大于10 Pa时，由真空夹层间气体的导热损失引起的真空管热性能变化已不明显，为了保证良好的真空管热性能，真空夹层的真空度应当维持在10-2Pa的数量级.

发射率；真空度；热损系数；空晒性能参数

1 引 言

真空管具有结构简单、价格便宜、安装和运输方便、保温性能好、光热转换效率高等优点[1]，因而在我国有着广泛的应用市场.

目前真空管性能的研究主要集中在理论分析与实验结合的方面，殷志强等人[2]从能量方程式推导出真空太阳能集热管的光-热性能参数，分析了真空管热性能的影响因素，提出了真空管空晒热性能评价标准，并做相应的实验进行验证.Ma[3]通过实验分析了空晒性能参数、闷晒太阳辐照量和平均热损系数三个参数对真空管热性能的影响，得出涂层发射比是影响真空管空晒性能参数和平均热损系数的主要因数，增大涂层吸收比可以提高真空管的闷晒性能.Badar等人[4]通过实验测量和数学模型相结合的方式分析了真空夹层内残余气体对真空管热量损失的影响，但热损测量值比理论值高.吴家庆等人[5]通过对全玻璃真空集热管的真空获得与真空寿命的研究表明：从良好的绝热效果和投资成本综合考虑，真空度选择在10-4～10-5托(1.33×10-2Pa～1.33×10-3Pa)为宜.Gui等人[6]研究了选择性吸收涂层发射率的影响，结果表明：真空管夹层间的压强在不大于5×10-2Pa时，由真空夹层间空气的导热引起的损失可以忽略.杨静芸等人[7]利用FLUENT对三腔式全玻璃真空管与常规全玻璃真空管在闷晒状态下管内流体的流动状态及性能进行数值模拟与分析，结果表明三腔式全玻璃真空管相较于常规全玻璃真空管具有启动速度快、温升高、管内流体流速大等特点.

本文采用数值模拟方法对Ø58×1 800 mm全玻璃真空管空晒状态下的热性能、管内工质的温度分布及变化情况进行模拟分析.探讨真空管高温状态下热损失机理及影响因数，为优化真空管的生产工艺和技术提供依据.

2 全玻璃真空太阳集热管热性能的影响因素分析

真空管在不同的辐射强度及环境温度下其空晒温度存在很大的差异，殷志强等人[2]通过大量的测试实验，分析得出了评价真空管空晒性能的参数

(1)

式中：Ac为真空管的有效采光面积(m2)；Aa为内管的表面积(m2)；τ为罩玻璃管透射比(AM1.5)；α为吸收涂层的吸收比(AM1.5)；G为太阳辐照度(W/m2)；Ul为热损系数(W/m2·K)；Ta为环境温度(K)；Tg为加热工质平均温度(K).从式(1)中可以看出，热损系数对真空管空晒性能参数起着决定性作用.真空管的热损主要有三个部分构成：不锈钢卡子和管口玻璃传导热损；吸收涂层的发射热损；真空夹层气体的导热.因此热损系数

σεT(Tg2+Ta2)(Tg+Ta)

(2)

式中：kg为真空管内不锈钢卡子和开口端玻璃传导损失kg≈0.003 2W/K[2]；K为真空管夹层气体的导热系数(W/(m·K))；εT为内管温度为T时吸收涂层的半球发射比.

3 数值模型及边界条件

选择市场常见的普通全玻璃真空管作为分析案例，真空管的外管管径为58mm，管长为1 800mm，内管管径为47mm，玻璃管壁厚为1.7mm，容积3.26L.根据全玻璃真空管的几何尺寸，利用ICEM构建网格模型.

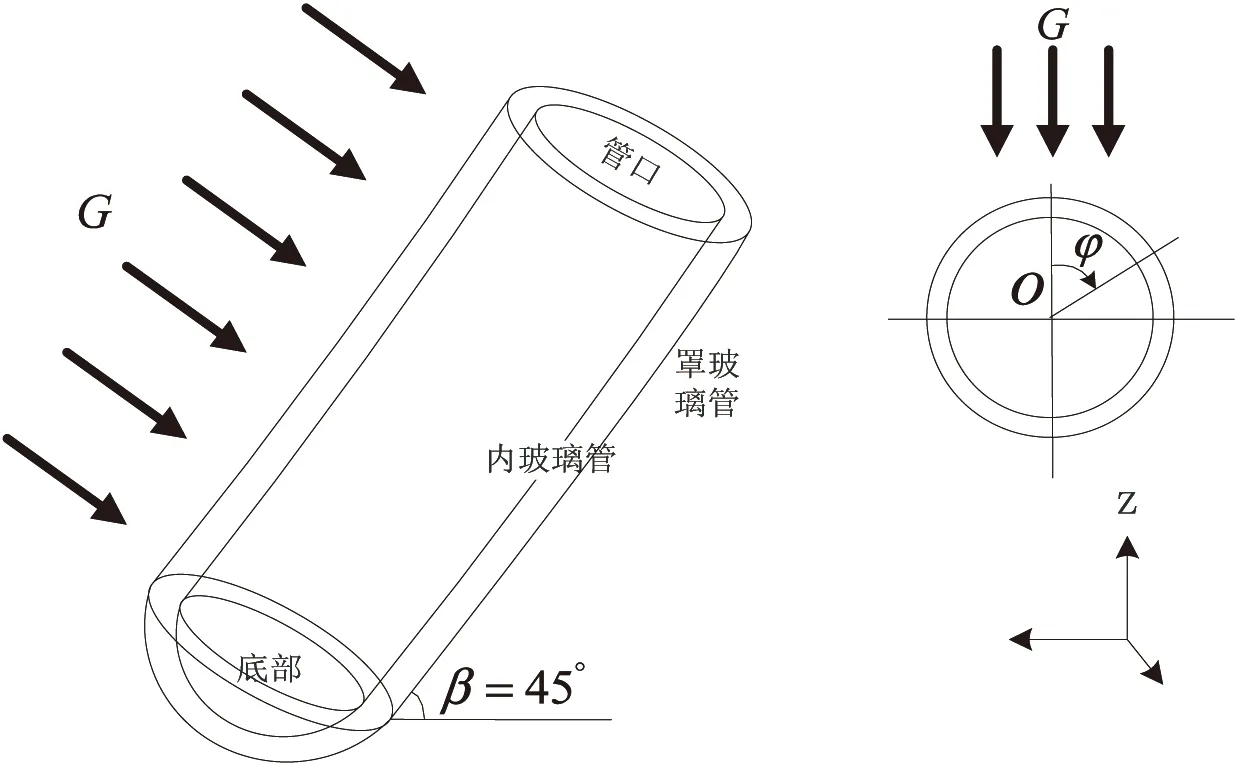
图1 全玻璃真空管空晒示意图

将ICEM生成的网格模型，导入Fluent中求解计算，根据实际辐射情况，建立辐射模型边界条件，真空管南北向放置，倾角45°，地点设置为昆明(E102°N25°)，模拟时间为2014年11月21日13时，其模型示意图如图1所示.为便于研究，需要对模型做以下几方面的假设:

1)采用Boussinesq假设，并假设在空晒条件下真空管内的空气随温度的热膨胀系数为1/273K;

2)真空管底部卡子无热传导损失；

3)忽略能量方程中的黏性耗散热；

4)涂层的吸收率和发射率不随温度的变化而改变；

5)真空管玻璃的物性参数均不随温度的变化而改变.

在不影响计算结果精度的前提下，为了减少FLUENT求解计算时间，需要进行网格独立性验证.分别计算了3种不同网格数下真空管空晒最高温度，结果见表1.对三种网格数下的计算结果进行对比可以得出，当网格数为174 477时，继续增加网格数量，空晒最高温度几乎不变，因此选择174 477的网格数进行求解计算.

表1 三种网格数网格独立性验证

4 实验验证

为了验证模拟结果的正确性，根据GB/T17049-2005[8]的方法及步骤进行了真空管空晒测试，分别选取5根透过率与吸收率相近的真空管，对应的发射比为0.028、0.031、0.041、0.06、0.082，测试期间太阳辐照度900～1 000W/m2，环境温度15～20 ℃，记录真空管内温度变化.利用FLUENT对发射比分别为0.04、0.06、0.08、0.1、0.12的真空管进行空晒数值模拟，并与测试结果进行对比.

图2为模拟与测试的空晒性能参数Y-ε的曲线，由图2可以看出，2条曲线变化趋势一致，真空管的空晒性能参数随发射率的升高呈现出降低的趋势，相同发射率下实验测得的真空管空晒性能参数比模拟结果平均低50K·m2·(kW)-1，这是由于真空管的涂层吸收比随温度的升高变化不大，而涂层发射比随空晒温度升高却迅速增大，史月艳等人[9]测量不同温度下AlN-Al真空管的发射比，结果表明300 ℃下真空管的发射比比80 ℃下真空管的发射比增加了57.1%.所以发射比在0.041、0.06、0.082时实验所测的空晒性能参数Y应近似等于发射比在0.06、0.09、0.12时模拟所得的空晒性能参数，从图中可以看出当模拟发射比比实验发射比大50%时，模拟与实验所得的空晒性能参数几乎相等.总体看来，模拟结果与实验测试结果吻合较好，所以通过模拟求解计算，用于分析真空管的热性能是合理的.

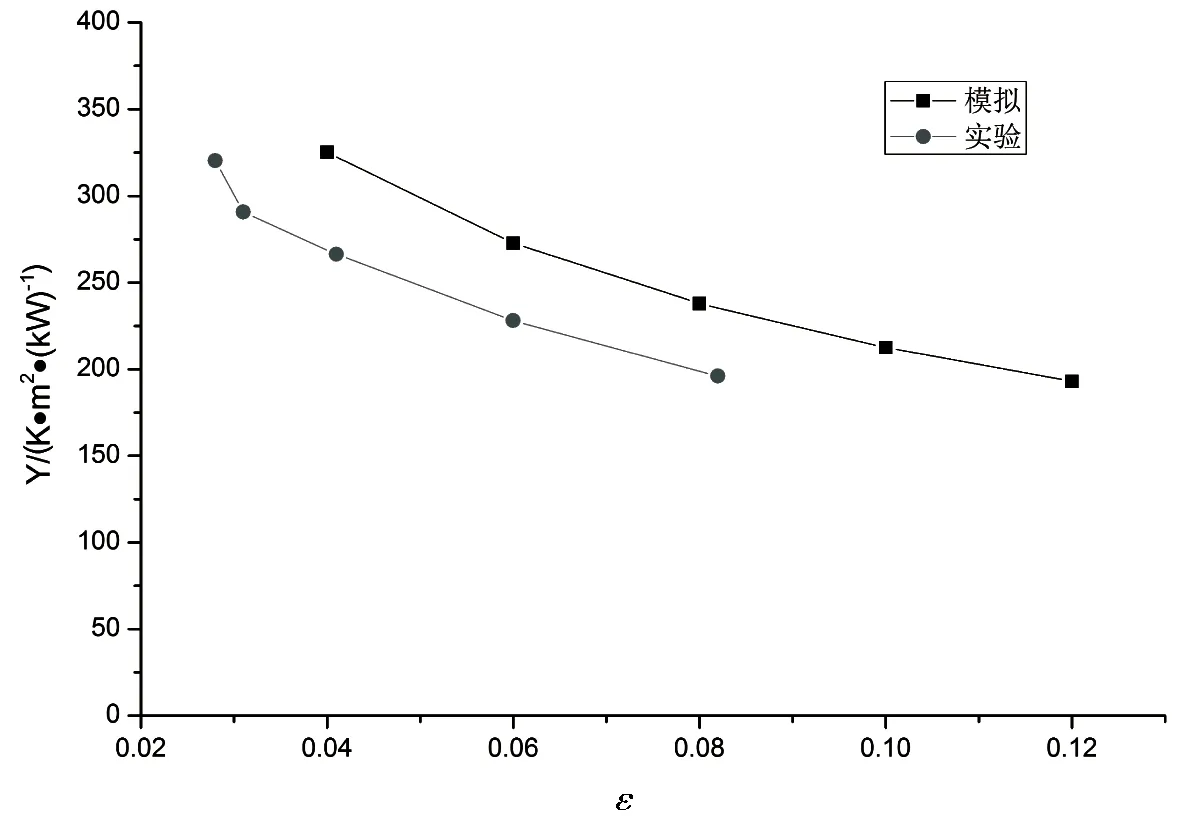
图2 空晒性能参数的数值模拟结果与实验对比

5 模拟结果与分析

5.1 发射率对真空管热性能的影响分析

1)不同发生率下真空管空晒温度对比

初始辐照G=988W/m2，环境温度为300K，τ=0.92，α=0.92，忽略真空部分的导热损失，分别将涂层的发射率设定为0.04、0.06、0.08、0.1、0.12，对真空管进行120min的辐射模拟求解计算，每隔10min取一次数据，将统计的结果进行整理分析得出不同发射率下，真空管内空晒温度随空晒时间的变化关系，如图3所示.从图中可以看出，不同发射率下真空管空晒温度曲线变化趋势相同，初始阶段，温度迅速升高，随着空晒时间的增长，温度升高的速率逐渐趋缓并达到相应的平衡状态，温度不再升高.发射率在0.04、0.06、0.08、0.1、0.12下分别对应的空晒温度为610K、560K、520K、480K，即发射率越低其空晒温度越高.

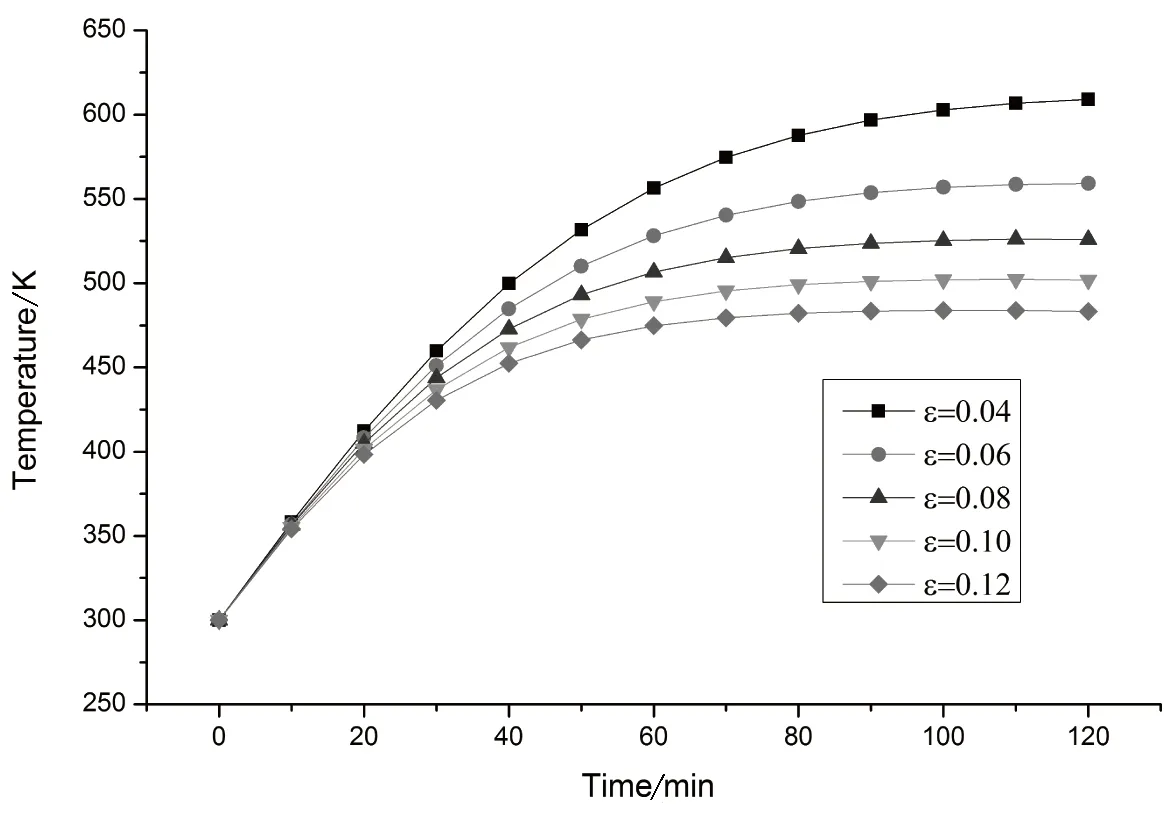
图3 不同发射率下真空管空晒温度随时间的变化

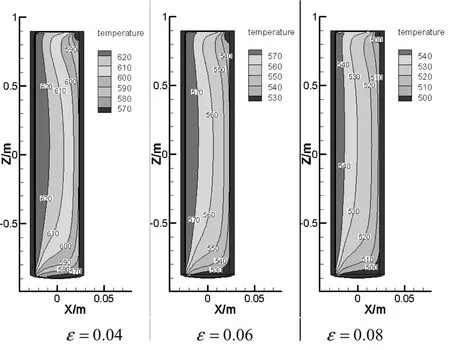
图4 不同发射率下真空管轴向截面的等温图

当真空管空晒温度不再升高时，截取真空管轴向截面，如图4所示，发射率分别为0.04、0.06、0.08时真空管内部温度的等温线图.从图中可以看出发射率低的真空管内部的整体温度明显高于发射率高的真空管内部的整体温度.图中等温度曲线显示，真空管中部温度变化较为均匀，加热壁面(左边为太阳辐射面)附近工质温度较高，向右温度逐渐降低.底部和顶部温度变化较大，且两端平均温度相对中部平均温度较低，这是由于真空管空晒情况下，由管口导热引起的损失较大，所以靠近管口的工质温度较低，而底部则是在密度差引起的热浮力作用下，使得管底部工质的温度低于中部工质温度.

2)发射率对真空管热损系数的影响

图5为辐射强度988W/m2，环境温度为300K，真空管的热损系数随空晒温度的变化关系，从图中可以看出真空管的热损系数随温度的升高逐渐增大，发射率越高，其曲线斜率越大，热损系数随温度的变化越明显.

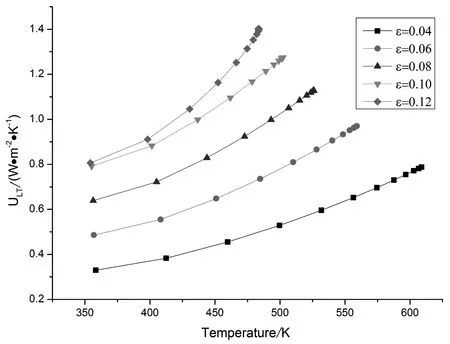
图5 真空管的热损系数随空晒温度的变化关系

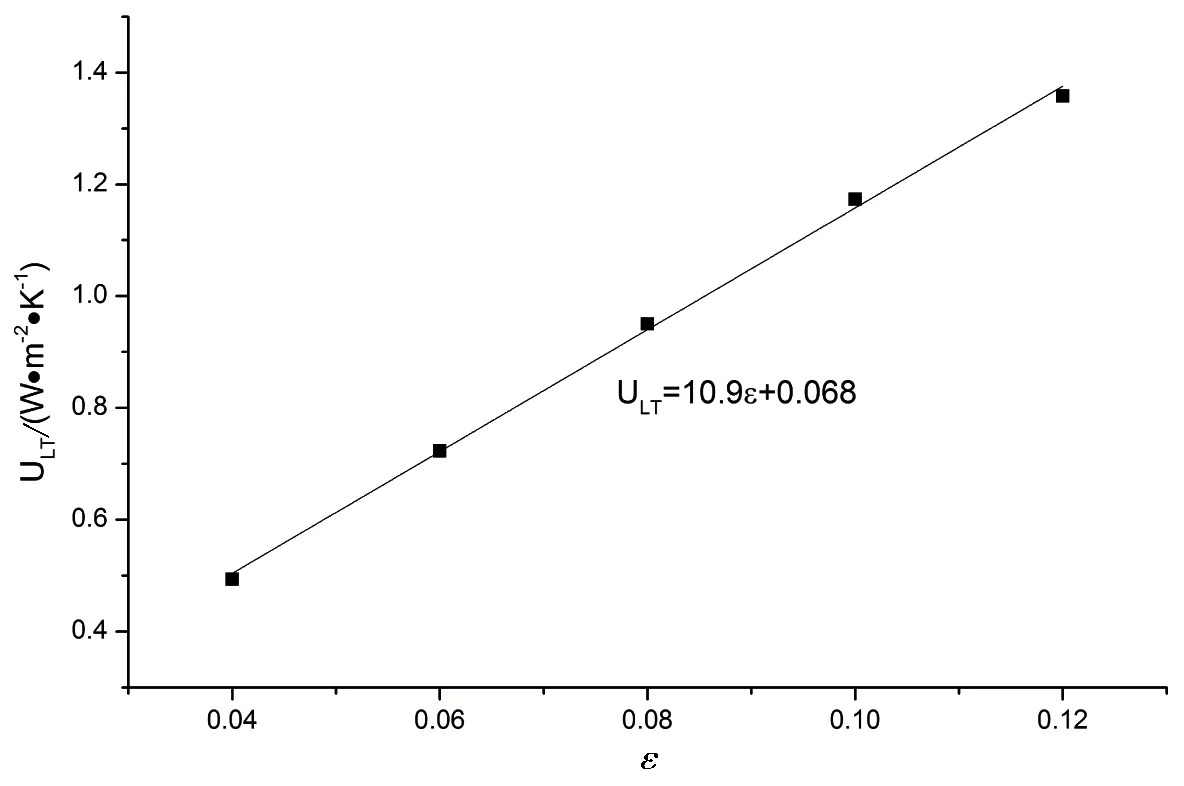
图6 热损系数随发射率的变化关系

图6为G=988W/m2，环境温度为300K，真空管空晒温度为480 ℃时，发射率与热损系数的关系，从图6中可以得出真空管的热损系数随发射率的增加几乎成线性正比例增加，其线性回归公式

(3)

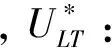
3)发射率对空晒性能参数的影响

如图7所示，真空管的空晒性能参数随涂层发射率的增加而减小，发射率为0.04时真空管的热性能参数为Y=325K·m2·(kW)-1，当发射率增加到0.12时真空管的热性能参数Y=193K·m2·(kW)-1，真空管的Y减少了132K·m2·(kW)-1，其拟合公式

Y*=350e-16.5ε+150

(4)

式(4)中，Y*为空晒性能参数(拟合值)，K·m2·(kW)-1.

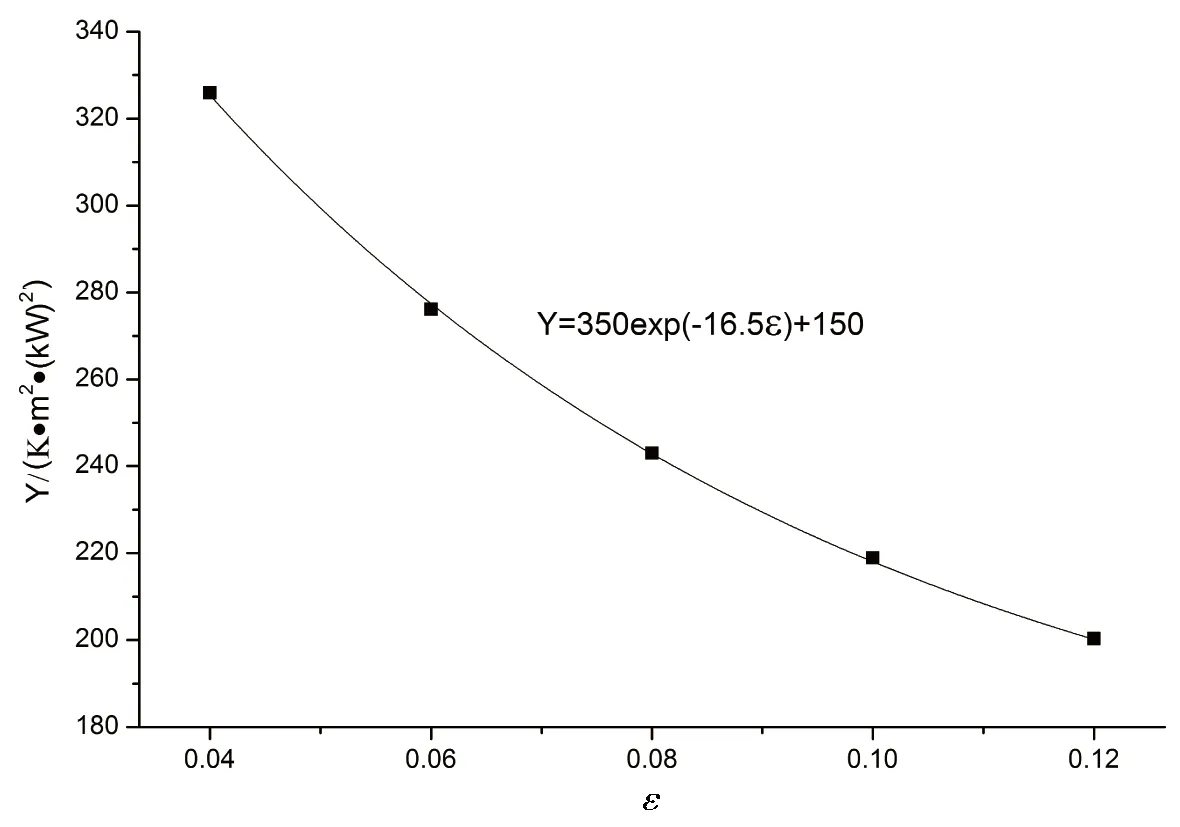
图7 真空管空晒性能参数Y与涂层发射率的关系

5.2 真空度对真空管空晒性能的影响

1)真空度对空晒温度的影响

为了探究真空夹层的真空度对真空管空晒性能的影响，分别选取了10-3Pa、10-2Pa、10-1Pa、1.0Pa、10Pa、102Pa、103Pa的真空压强进行模拟求解，辐照G=988W/m2，环境温度为300K，ε=0.06，α=0.92，τ=0.92，对真空管进行120min的辐射模拟求解计算，分析模拟结果，得到真空管内空晒温度随时间的变化关系，如图8所示.从图8中可以看出，真空管内的空晒温度开始一段时间内温度迅速升高，随着空晒时间的增长，温度升高速率逐渐趋缓，最后达到相应的平衡状态，温度不再升高.真空管夹层间的压强越大，空晒最高温度越低，达到平衡状态所用时间就越短.

当真空管空晒温度不再升高时，截取真空管轴向截面，得到压强分别为1.0×10-3、1.0Pa、1.0×105Pa时真空管内部温度等温线图，如图9所示.图中真空管的左侧为太阳辐射壁面，所以左侧温度较高，右侧温度较低；压强低的真空管内部的整体温度明显高于压强高的真空管内部的整体温度；真空管中部温度变化较为均匀，顶部和底部温度变化较大，且平均温度相对中部温度较低.这是由于真空管在空晒情况下，管内温度较高，由管口导热引起的损失较大，所以靠近管口的工质温度较低，而底部则是在密度差引起的热浮力作用下，使得真空管低部工质的温度低于中部工质温度.

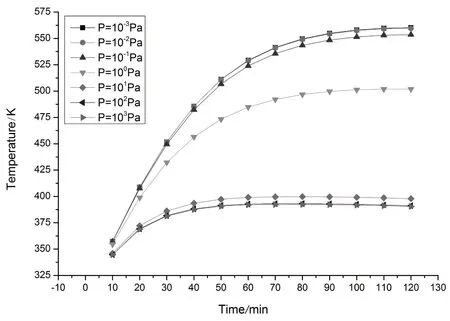
图8 真空管空晒温度随时间的变化的关系

图9 不同真空度下真空管轴向截面的等温图

2)真空度对热损系数的影响

图10表示不同真空度下真空管的热损系数随空晒温度的变化关系，不同曲线分别对应着不同的真空度，真空管的热损系数随温度的升高逐渐的增大，压强位于10-3Pa、10-2Pa、10-1Pa时，热损系数随温度变化的曲线几乎重合，空晒温度560K下的热损系数1.0W/(m2·K)比空晒温度355K下的热损系数0.5W/(m2·K)增加了一倍.然而当压强高于1.0Pa时，其热损系数将不随温度的增加而增加.

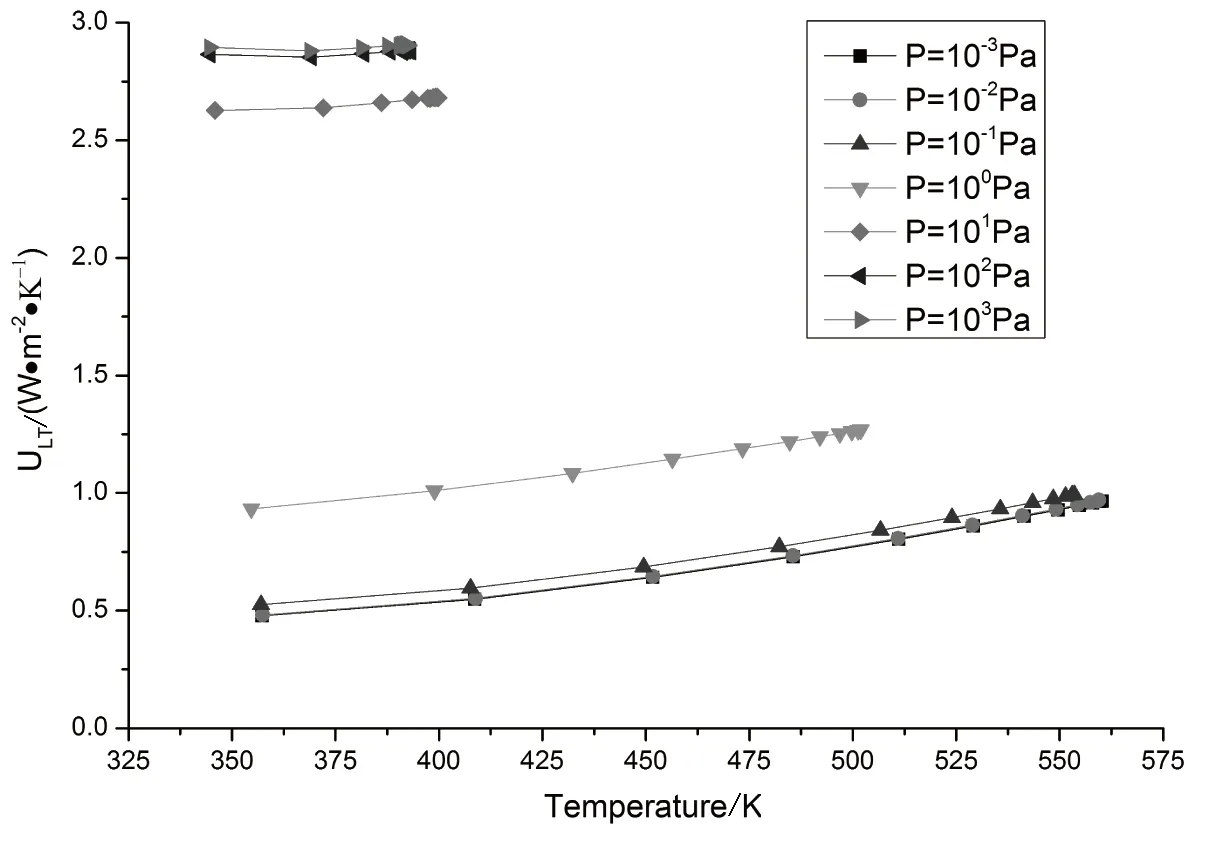
图10 不同真空度下热损系数随空晒温度的变化关系

如图11为空晒温度390K时真空管的热损系数随真空度的变化关系，从图中曲线可以看出压强为10-1～10Pa是热损系数变化最为明显的区域，当压强从10-1Pa升高到10Pa时，热损系数从0.5W/(m2·K)增大到2.7W/(m2·K).当压强小于10-1Pa或大于102Pa时，热损系数的变化很小.

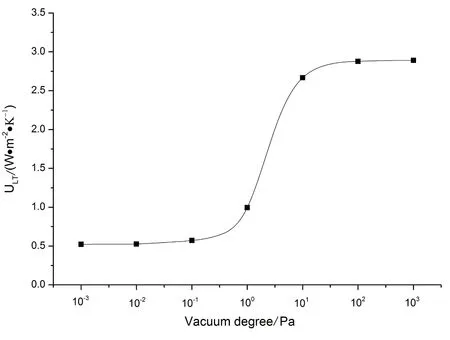
图11 热损系数随真空度的变化关系

3)真空度对空晒性能的影响

图12为真空管空晒性能参数随真空度的变化关系，真空管的空晒性能参数随压强的升高而降低，从图12中可以看出空晒性能参数随压强的变化主要位于10-1～10Pa的范围，其空晒性能参数从264K·m2·(kW)-1下降到102K·m2·(kW)-1，当压强小于10-1Pa或大于10Pa时热损系数变化很小.所以为了保证良好的真空管热性能，通常需要将真空管夹层间的压强维持在10-2Pa的数量级.

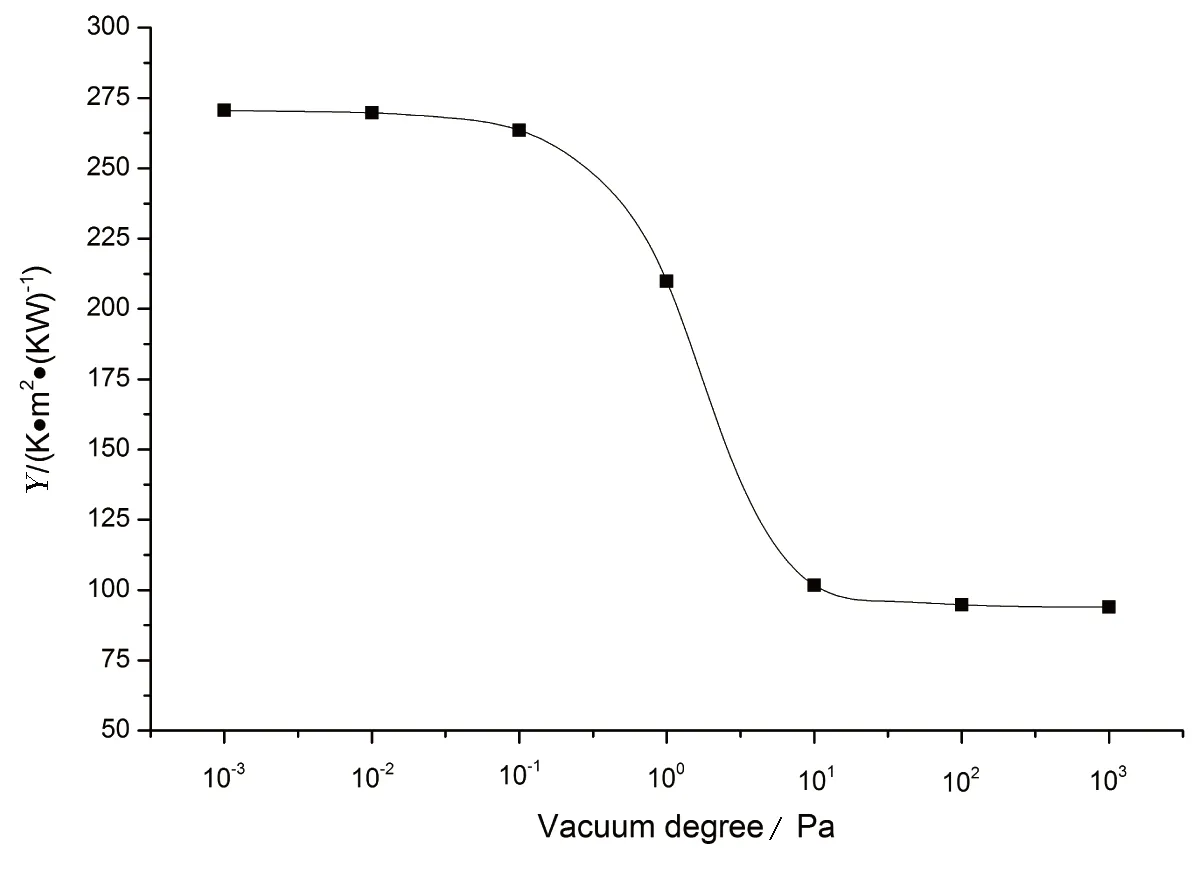
图12 真空管空晒性能参数与真空度的关系

6 结 论

通过对全玻璃真空管的空晒性能及其影响因素模拟分析，得出以下结论：

1)影响真空管空晒性能的主要参数为发射率和真空度.

2)真空管的热损系数随发射率的增加而增大，且同一发射率下其热损系数随真空管空晒温度的升高而增大，发射率升高真空管的空晒性能参数下降.

3)真空管空晒性能变化主要位于10-1～10Pa范围，当压强小于10-1Pa或大于10Pa由真空夹层间气体导热损失引起空晒性能的变化很小，所以为了保证良好的真空管热性能，通常需要将真空管夹层间的真空度维持在10-2Pa的数量级.

4)涂层发射率越低，由辐射引起的热损失就越小，真空管的热性能越好.

[1]YINZHIQIANG.DevelopmentofsolarthermalsystemsinChina[J].SolarEnergyMaterials&SolarCells,2005,86:427-442.

[2] 殷志强，唐轩．全玻璃真空太阳集热管光-热性能[J]．太阳能学报，2001，22(1)：1-5．

[3]MAFANGFANG,GAOWENFENG,LIUTAO,etal.Anexperimentalstudyontheimpactsofkeyparametersofall-glassevacuatedtubesonthethermalperformancesofall-glassevacuatedtubesolarwaterheaters[J].J.RenewableSustainableEnergy,2013，5(2)：347-355.

[4]ABDULWAHEEDBADAR,REINERBUCHHOLZ,FELIXZIEGLER.Experimentalandtheoreticalevaluationoftheoverallheatlosscoefficientofvacuumtubesofasolarcollector[J].SolarEnergy,2011,85(7):1447-1456.

[5] 吴家庆，陶祖岩，王凤春,等．玻璃真空集热管的真空获得与真空寿命[J]．清华大学学报，1982，22(2)：142-148．

[7]GUIYUZONG,XUEZUQING,ZHOUXIAOWEN,etal.Determinationofemittanceofselectiveabsorbingsurfaces[J].SolarEnergy,1998,64(4-6):241-243.

[8] 杨静芸，高文峰，刘滔，等．三腔式全玻璃真空管闷晒性能的数值模拟及实验验证[J]．太阳能，2014，12(12)：55-60．

[9]GB/T17049-2005，全玻璃真空太阳集热管[S]．

[10]殷志强，史月艳，林子为．用于全玻璃真空集热管的黑镍选择性吸收涂层[J]．清华大学学报，1982，22(4)：49-58．

Numerical Simulation and Analysis on Stagnation Performance of All-glass Evacuated Collector Tubes

LIU Bai-hong, GAO Wen-feng, LIU Tao, LIN Wen-xian, XING Xiu-lan, HU Xiao-fang

(Solar Energy Research Institute,Key Laboratory of Advanced Technique & Preparation for Renewable Energy Materials of the Ministry of Education of China,Yunnan Normal University,Kunming 650092,China)

In this paper, FLUENT has been used to simulate and analyze the stagnation performance of all-glass evacuated tubes,which size is Ø58×1 800mm,with different emittance and vacuum degree.In addition, the accuracy of numerical simulation also being verified through test.The numerical simulation results show that the lower is the emittance,the smaller is the heat loss and the better is the thermal performance of all-glass vacuumed tubes. What′s more, the stagnation performance of all-glass evacuated tube decreases with the increase of the air pressure in the vacuum jacket. The stagnation change of all-glass evacuated tube mainly in the range of 10-1～10 Pa. When the air pressure is lower than10-1Pa or greater than 10 Pa,the thermal performance change caused by heat conduction loss of air in the vacuum jacket is not obvious.Therefore the vacuum degree of air jacket should maintain in the order of 10-2Pa in order to guarantee good thermal performance of all-glass evacuated tube.

Emittance; Vacuum degree; Heat loss coefficient; Stagnation parameter

2015-06-10

国家自然科学基金资助项目(51266016，51469035).

刘佰红(1989-)，男，河南信阳人，硕士研究生，主要从事太阳能热利用及计算流体力学方面研究.

高文峰(1970-)，男，副教授，主要从事太阳能热利用及计算流体力学方面研究.E-mail:413900096@qq.com.

TK513

A

1007-9793(2015)04-0005-06