一类控制方向未知不确定性系统的自适应迭代学习控制*

李广印， 孙云平, 贾纳豫

(1.云南师范大学 信息学院,云南 昆明 650092;2.玉溪师范学院 信息技术工程学院,云南 玉溪 653100)



一类控制方向未知不确定性系统的自适应迭代学习控制*

李广印1， 孙云平1, 贾纳豫2

(1.云南师范大学 信息学院,云南 昆明 650092;2.玉溪师范学院 信息技术工程学院,云南 玉溪 653100)

采用了一种自适应迭代学习的控制方法,对于一类含有未知控制方向以及参数化和非参数化不确定性系统进行了研究.结合连续的Nussbaum增益技术,很好地处理了系统中控制方向未知的问题.在满足局部Lipschitz连续条件下,非参数化不确定性可以得到有效的解决.通过构造微分-差分耦合参数自适应律,提出一种自适应迭代学习控制方案,保证系统跟踪误差沿迭代轴方向渐进收敛于零.基于一个构造的Lyapunov泛函,给出闭环系统收敛的一个充分条件.实例仿真结果验证了设计方法是有效的.

不确定性系统;Nussbaum增益;未知控制方向;局部Lipschitz连续;Lyapunov泛函

1 引 言

迭代学习控制(ILC)能够高效的处理在一个有限的时间区间上的各种控制跟踪以及周期扰动问题,它的基本思想是基于前一次操作的错误信号来修正当前的控制输入,以此达到提高响应质量的效果[1-2].对于迭代学习控制的研究还存在如下问题.

一是关于系统的初始条件问题.系统初始条件可分为相同的初始条件和对接条件两种情况.在迭代学习控制中相同的初始条件要求在每一个迭代过程有相同的初始状态,而对接条件则将上一次迭代的结束状态作为当前迭代的初始状态,同样要求参考目标在每一次迭代过程当中的初始状态参数等于末尾状态参数.基于压缩映射的迭代学习控制,要求相同的初始条件是非常有必要的[4],其本质上是为了能够产生一个能够收敛到某一个固定点的序列，但是在实际应用中要求比较完美的重置效果,实现起来还是比较困难的.初始条件存在细微的误差就有可能导致系统跟踪误差的发散[1].为了削弱系统的限制条件进行了大量的尝试工作,对接条件在实际应用当中好像表现得更为出色.文献[1,3]针对一类一阶参数化迭代学习控制系统,利用Lyapunov技术[4],基于五种不同的初始条件进行了讨论.文献[5]基于对接条件对自适应迭代学习控制进行了探究.

二是控制方向未知的问题.控制方向在系统的设计过程起着关键性的作用.在许多事实结果当中,都会做一个很有必要的控制方向已知的假设,为了不失一般性,然后继续假设方向为正的情况.然而,在一些特殊情况下,很难根据物理意义判别系统的控制方向.现在Nussbaum增益技术是解决控制方向未知问题的一种常用方法[6-8].

怎样处理系统的不确定性是第三个问题.系统不确定性一般都假设能够参数化[9-10],系统不确定性的结构是知道的,但是只能对一些未知常参数或未知周期时变的参数进行适当的参数化.所以,基于参数化的迭代学习控制方法的分析以及性能都依赖于上述假设,当参数化假设不满足时,这种方法就会不起作用[11].但是,还没有涉及双线性耦合参数的参数化问题.本文设计了一种自适应迭代学习控制方案,基于对接条件,对于含有未知控制方向以及参数化和非参数化不确定性系统进行了讨论.通过设计的自适应控制策略,使得跟踪误差沿迭代轴方向渐进趋于零.然后利用构造的一个Lyapunov泛函,给出闭环系统收敛的一个充分条件.数值仿真结果验证了所设计方法是有效的.

2 问题描述

考虑下列非线性不确定系统：

(1)

其中i是迭代次数,t∈[0,T],T是一个已知大于零的常数.xi=[x1,i,x2,i]T∈R2为可测的系统的状态向量,ui(t)∈R为系统的控制输入,ϑ(t)∈R为连续未知的时变参数,θ∈R为未知的常参数,ξ(xi,t)∈R为已知的连续非线性函数,f(xi,t)为一个未知非线性函数.b≠0为一个符号及值均未知的常参数,b的符号决定系统的控制方向.

对于给定的参考信号xd(t)∈R2，有：

(2)

其中xd=[xd,1,xd,2]T∈R2,s(xd,t)是一个已知的光滑函数,xd(0)是参考信号的初值.

假设1θ是一个未知常参数,但是符号已知,可以设定θ>0.

假设2xi(0)=xi-1(T)，xd(0)=xd(T).

假设3f(x,t)是非线性函数,满足局部李普希茨连续条件,即

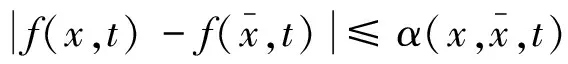
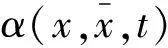
定义1ν(·)是一个光滑的Nussbaum函数,具有以下特点:

(3)

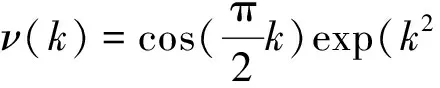
引理V(·)和k(·)是定义在区间[0,tf]上的光滑函数,∀t∈[0,tf],V(t)≥0，ν(·)是一偶的光滑的Nussbaum类型函数,b≠0是一个已知的常数,如果下列不等式成立:

(4)

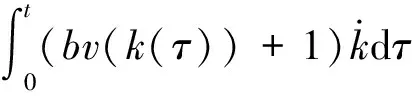
3 自适应迭代学习控制设计

对于∀t∈[0,T],跟踪误差动态方程如下

(5)

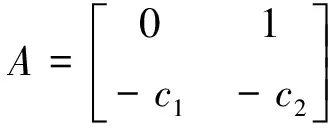
ATP+PA=-Q

(6)

因此,对∀w∈R2,不等式-wTQw≤-λQ‖w‖2都成立,其中λQ是矩阵Q的最小特征值.

定义Lyapunov函数

(7)

对(7)式中的V1,i(t)求导得

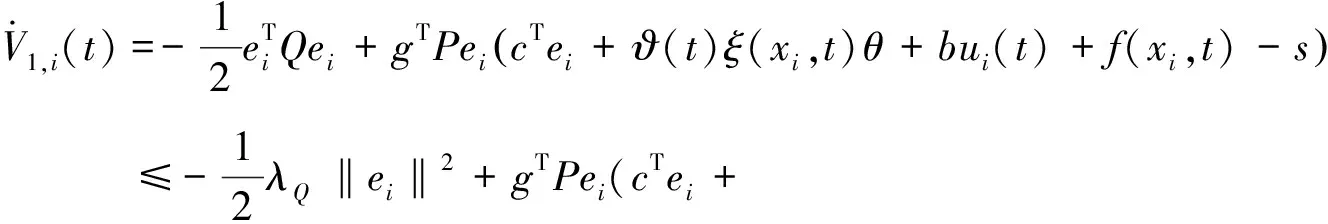
(8)

根据假设3,利用Young's 不等式,可得

(9)

将(9)式代入(8)式得

(10)

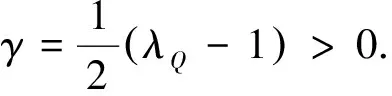
构造的第i次迭代的学习控制律如下:

(11)

时变参数ϑ(t)的学习律为:

(12)

时不变参数θ的学习律为:

(13)

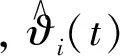
投影函数proj(·)定义为:

(14)

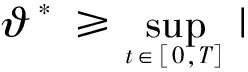
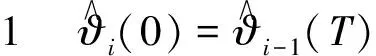
证明 首先证明第一个式子.

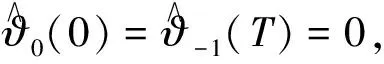
(15)

由(12)式可得

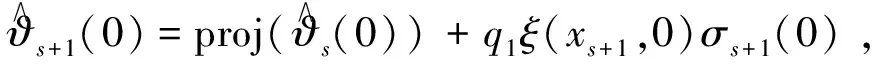
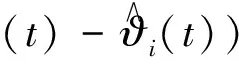
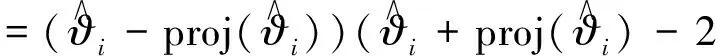
(16)

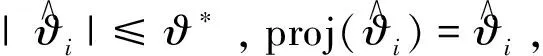
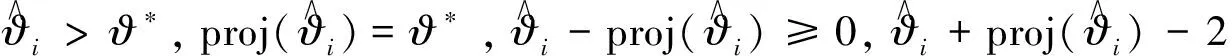
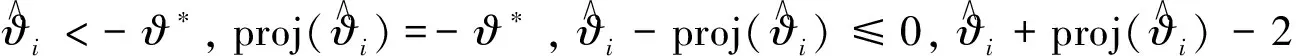
4 收敛性分析

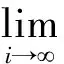
证明 构造的Lyapunov泛函为

(17)

对任意t∈[0,T],Vi(t)在区间[0,T]上的差分为

(18)

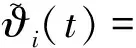
根据(10)式,计算(18)式右边第一项,得

(19)

(20)

根据参数学习律(13)式,计算(18)式右边第四项,得

(21)

把(19)、(20)和(21)式分别代入(18)式

(22)

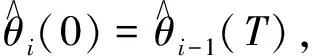
(23)

重复利用(23)式可以得到

(24)

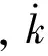
(25)

可以进一步得到Vi(t)的导数为

(26)

从而求得

(27)

定义E(t+(i-1)T)=Vi(t),对任意∀t∈[0,T].由(25)式和(27)式得

(28)

当i→,可以得到

(29)

下面证明V0(T)的有界性

(30)

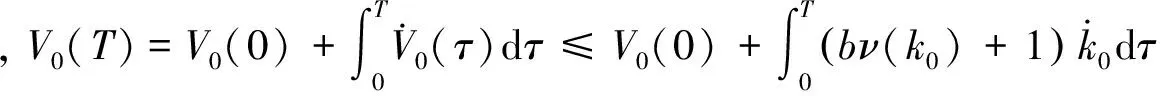
(31)

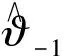
(32)

因为ϑ(t)在区间[0,T]上连续,所以ϑ(t)在区间[0,T]上有界,又因为θ是未知常数,所以存在如下有限正常数

(33)

将(33)式代入(32)式

V0(0)=M1+M2+M3<

(34)

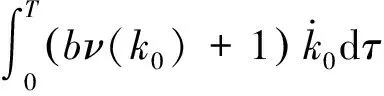
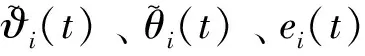
5 仿真例子

考虑如下时变系统

(35)

目标轨线

(36)

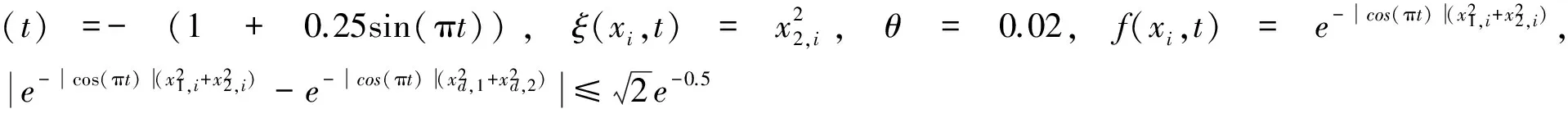
情况1 当b>0时,取b=4,最大跟踪误差|ei|sup的曲线如图1所示,Nussbaum增益函数ν(·)的曲线如图2所示,时变参数ϑ(t)的估计曲线如图3所示,时不变参数θ的估计曲线如图4所示,控制律ui(t)的曲线如图5所示.

情况2 当b<0时,取b=-4,最大跟踪误差|ei|sup的曲线如图6所示,Nussbaum增益函数ν(·)的曲线如图7所示,时变参数ϑ(t)的估计曲线如图8所示,时不变参数θ的估计曲线如图9所示,控制律ui(t)的曲线如图10所示.

图1 最大跟踪误差的曲线 图2 Nussbaum-type函数的曲线

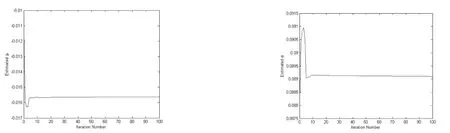
图3 时变参数ϑ(t)的估计曲线 图4 时不变参数θ的估计曲线

图5 控制器ui(t) 图6 最大跟踪误差的曲线

图7 Nussbaum-type函数的曲线 图8时变参数ϑ(t)的估计曲线

图9 时不变参数θ的估计曲线 图10 控制器ui(t)

6 结 论

基于对接条件,对于含有未知控制方向以及参数化和非参数化不确定性系统,提出了一种自适应迭代学习的控制方法.利用Nussbaum增益技术,使得系统控制方向未知的问题得到处理.双线性耦合参数的参数化问题的解决得益于构造的微分-差分耦合参数自适应律.系统的非参数化不确定性输入增益通过满足局部Lipschitz连续条件也得到了很好的处理.最后在设计的自适应迭代学习的控制方案下,使得系统的跟踪误差沿着迭代轴的方向逐渐趋向于零.基于构造的一个Lyapunov泛函,给出了闭环系统内所有信号有界的一个充分条件.实例数值仿真结果验证了该方法是有效的.

[1]XUJX.Asurveyoniterativelearningcontrolfornonlinearsystems[J].Int.J.Control.，2011,84(7):1275-1294.

[2]ANHSH,CHENYQ,MOOREKL.Iterativelearningcontrol:briefsurveyandcategorization[J].IEEETrans.Syst.ManCybern，2007,37(6):1109-1121.

[3]XUJX,YANR,CHENYQ.Oninitialconditionsiniterativecontrol[J].IEEETransactionsonAutomaticControl，2005,50(9):1349-1354.

[4] 雷靖，黄俊娇.非线性系统基于李雅普洛夫第一方法的控制律设计[J].云南民族大学学报：自然科学版，2014，23(4)：262-265.

[5]YANGZ,CHANCW.Conditionaliterativelearningcontrolfornon-linearsystemswithnon-parametricuncertaintiesunderalignmentcondition[J].IETControlTheoryandApplications，2009,3(11):1521-1527.

[6]NUSSBAUMRD.Someremarksonaconjectureinparameteradaptivecontrol[J].System&ControlLetters，1983,3(11):243-246.

[7]YUM,YEXD,QIDL.Robustadaptiverepetitivelearningcontrolforaclassoftime-varyingnonlinearsystemswithunknowncontroldirection[J].ControlTheoryAppl，2013,11(3):336-342.

[8]XUJX,YANR.Iterativelearningcontroldesignwithoutaprioriknowledgeofthecontroldirection[J].Automatic，2004,40(10):1803-1809.

[9] 郑平安，孙云平，杨昆，等.含有时变延迟的双线性参数化系统的重复学习控制[J].云南师范大学学报：自然科学版，2014,34(1):1-8.

[10]SUNMX,WANGDW,CHENPN.Repetitivelearningcontrolofnonlinearsystemsoverfiniteintervals[J].ScienceChina，2010,53(1):115-128.

[11]YANGZY,YAMSCP,LILK,etal.Universalrepetitivelearningcontrolfornonparametricuncertainandunknownstate-dependentcontroldirectionmatrix[J].IEEETransactionsonAutomaticControl，2010,55(7):1710-1715.

Adaptive Iterative Learning Control for a Class of Uncertain Systems with Unknown Control Direction

LI Guang-yin1, SUN Yun-ping1, JIA Na-yu2

(1.School of information,Yunnan Normal University,Kunming 650092,China；2.School of Information Technology and Engineering,Yuxi Normal University,Yuxi 653100,China)

A method of adaptive iterative learning control is searched for a class of uncertain systems with unknown control direction and both parametric and non-parametric uncertainties.A technique of the continuous Nussbaum gain is incorporated into the control design to counteract the lack of a priori knowledge of the control direction which determines the motion direction of the system under any input.Nonparametric uncertainties satisfying local Lipschitz continuous condition can be effectively handled. A new adaptive iterative learning control mechanism is constructed with both differential and difference updating laws to guarantee the asymptotic convergence of the system tracking error sequence along the iteration axis. Based on a constructed Lyapunov functional,a sufficient condition of the convergence of the closed-loop system is given.The simulation result shows the effectiveness of the proposed method.

Uncertain systems; Nussbaum gain; Unknown control direction; Local Lipschitz continuous; Lyapunov functional

2014-11-15

国家自然科学基金资助项目(61164017)；云南省科技厅基金资助项目(2010ZC069)；云南省教育厅基金资助项目(2010Y006，2014Y412).

李广印(1989-),男, 河南安阳人，硕士研究生,主要从事自适应控制与学习控制方面研究.

孙云平.E-mail:sunypxd@163.com.

TP13

A

1007-9793(2015)04-0019-09