数学课堂中的“逆势而为”

谢家文

一、在“逆例（型）”中导入，培养逆向思维意识

大部分数学知识有着一定的生活原型，教师喜欢在新授教学的导入环节寻找生活原型，创设有明显生活原型的教学情境，唤醒学生已有的生活体验，试图拉近知识与学生的距离，让学生学得轻松而精彩。其实有不少生活原型，学生本来很熟悉了，课堂上还利用它们，学生容易熟视无睹，不但提不起兴趣，也难以引发他们对生活原型的真正思考。如果此时能逆着生活原型创设情境，就会产生认知冲突，吸引他们往深层次思考。

例如，“轴对称图形”一课的教学。一位教师并没有戴着生活中两边大小一样的眼镜进入课堂，而是一大一小，与生活原型不同。全班一片笑声，笑声过后，教师问道：“为什么笑？”学生说：“两边大小不一样，很滑稽。”教师追问：“怎么知道不一样？你能用什么方法证明吗？”学生反馈：“把眼镜对折。”教师又步步紧逼：“如果眼镜不能对折呢？”经过学生的讨论，最终得出：“把它们放在纸上描画出来，就可以对折。”教师顺势引出概念：“如果一个图形沿着一条直线对折后两部分完全重合，这样的图形就叫作轴对称图形。”轴对称图形的产生过程就这样一步步地呈现出来。这里得益于教师创造了一个不对称的生活实例，引发学生认知冲突，从而很自然地抽象出轴对称图形的本质特征，形成概念。在数学教学中多一些逆向的生活实例引入新课，不但能引发认知冲突，深化认知，还能培养学生对生活中习以为常的生活现象、生活例子多一些逆向的眼光，从而培养逆向思维意识。

二、在逆思中新授，培养逆向思维意识

先入为主——先听进的话或先获得的印象，往往在头脑中占主导地位。此话映射在教学上就是——教师新授时的思维方向对学生的思维意识起着举足轻重的作用。为此，在新授时，笔者会思索例题教学思路的互逆性，时常会引导学生逆向思考例题的解题思路，以训练学生的逆向思维意识。

例如，在教学习题：“成人票24元，儿童票半价。星期天，爸爸妈妈带着玲玲去‘冰雪天地游玩。购门票需要花多少钱？”常用的正向思维是：“爸爸的票钱+妈妈的票钱+玲玲的票钱=一共要的钱”，这也是例题中两种常规解法的思路依据。当这两种解法学生都明白了，笔者追问学生：“如果反过来用减法可以吗？”学生在讨论与思考中得出：“看作三个成年人的钱-玲玲少用的钱=一共要的钱。”逆向思路也解出来了，学生感到很兴奋，也感受到了成功的喜悦。多几次对例题解法的逆向追问、逆向思考与逆向探索，学生的逆向思维意识就能得到培养。

三、在“逆练”中练习，培养逆向思维意识

在例题教授环节完成后，不少教师喜欢变换条件去训练学生，不断强化例子所传递出的解题方法，只要学生熟练了，就立刻停止采用这种方式训练学生：一方面，学生很容易僵化，易养成按部就班的惰性思维——“唯书论”，学生的创新求异思维不易发展；另一方面，很多学生会练得很枯燥，不利其积极情感态度的形成。其实，还可以进行一些逆思维练习，打破学生对常用解法的惯性认识。常用的“逆”练习有两种形式：一是逆着教材的格式进行练习。这就是一种最简单的逆向思维练习，在低年级教学中可以经常使用。

例如，“20以内数的认识”一课。学生能熟练地从1数到20后，教师不能仅局限于此，还要求学生会从20倒着数到1，会填一些倒着数的数格练习。在教学“10以内的加法”后，教师不但要让学生练“3+4=？”这样正向形式的练习，还要让他们练习“7=□+□”这种逆向形式的练习，能满足学习层次不同的学生的学习需要。二是逆着教例的解题方法去练。例如，“乘数是两位数的小数乘法”，例题的方法是被乘数先乘乘数的个位再乘十位（即从低位开始乘的方法）。练习时，当学生会用这种方法计算，且比较熟练后，教师说：“是不是一定要从乘数的低位开始乘起呢？我们能不能反过来从乘数的高位开始乘起呢？”学生的探究热情高涨，经过尝试，发现完全可以。为了印证这种方法的可行性，教师道出了市场上很多菜农不借助计算器，却很快算出总价的奥秘。

这样“逆”着练，不但丰富了解法，适应不同层次学生的发展需要，更重要的是能打破学生的常规思维，开拓求异思维，从而发展学生的逆向思维意识。

四、在“逆追”中归纳，培养逆向思维意识

知识自成体系，但它散落在各册教材或各个课时中，学完一部分知识后，教师都要组织学生进行归纳，促使知识系统的形成，常用的方法是顺着知识的推进过程进行归纳，这种方式有一个缺点：学生凭着知识学习先后顺序的自然感觉去归纳，没有真正去思考为什么这样构网成络，缺乏对知识之间内在逻辑联系的思考。在教学时，笔者常逆着知识的进程进行归纳。

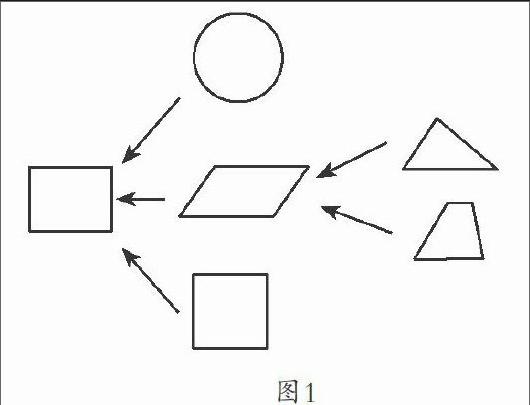
例如，在学习“圆面积计算”一课，小学阶段平面图形部分的认识也结束了。为构建知识系统，笔者进行了总结。总结时，笔者不是顺着图形的先后学习顺序及内在联系去归类总结，而是从最后学的圆形逆过来去追寻知识系统，直接提问：“我们学了许多平面图形，今天来构建知识树，如果从刚学的圆逆推回去，你认为圆的上一层平面图形是什么？为什么？”于是学生就从已学过的平面图形（长方形、正方形、平行四边形、三角形、梯形）中去寻找，通过分析它们之间的内在“机理”，发现圆可以转化成长方形，得出圆的上一层知识点是长方形。针对在分析中学生知道了梯形和三角形不是圆的上一层知识点，笔者追问道：“既然梯形不是圆的上一层知识点，那么梯形的上一层知识点是什么呢？”学生构建出“梯形→平行四边形”的知识联结，接着放手让学生运用逆推思维和平行思维去寻找各种平面图形的关系，最终形成这样的知识树（如图1），学生在追溯过程中，找到了小学阶段的平面图形知识的根是长方形，同时理清了各种图形之间的逻辑关系，使这些散乱的知识，变成了一串有序、紧密联系的知识链。教学中，多一些这种寻根溯源的逆向归纳总结，学生不但能深入分析知识间内在的逻辑关系，形成深刻的知识链，而且在逆向寻“根”中，培养了学生的逆向思维意识。

（作者单位：福建省长汀县城关中区小学 责任编辑：王彬）endprint