基于部门利益下的集体决策与投票博弈
2015-04-29刘振彬
刘振彬


摘 要: 部门利益下的集体决策与投票由于影响因素的不同可能会得出许多不同的结果。在建立基于利益相关部门之间、利益相关部门与其他部门之间、利益无关的各个部门之间视角下的假设基础上,讨论了这三种情况下对集体决策与投票的影响模型,分析其在实际运行中的可能性。通过对三种博弈模型的分析与归纳,探讨了公共部门人事管理中的集体决策逻辑。
关键词: 部门利益; 博弈; 集体决策与投票; 假设
中图分类号: F 045.6 文献标志码: A 文章编号: 1671-2153(2015)01-0093-04
0 引 言
无论是从国家层面上看西方的多党制还是两党制到中国的人民代表大会制,还是从现代企业董事会制到一般组织的少数服从多数的基本定律,现代民主社会的发展似乎在一直强调着:集体决策与投票才是最重要的。熊彼特曾经指出,民主是重要的,因为它使当局的立场合法化以及投票承载着一种信任,一种政治体系或政治制度得到了承认,即被合法化了。透过熊彼特的观点,我们可以这样认为,民主之所以重要,因为它是基于集体决策与民众投票下的民主,它的存在是人们追求公平正义的结果。集体决策能够让我们很大程度上避免了专政与暴政的存在,减少个人偏见对决策的影响,投票又让多数人表达了个人的利益与诉求,让多数人的选择偏好得到集中反映。
在涉及整个组织利益的重要决策中,集中的集体决策与投票往往是必不可少的环节。那么,在部门利益的视角下,利益相关部门之间、利益相关部门与无关利益部门之间、部门与部门之间的决策选择对集体决策的结果产生什么样的影响,其结果与预期是否一致,能否实现资源的最优配置以及人们所期望的效率,或者最大程度上实现了公平正义?在此背景下,本文试图通过基于部门利益的若干视角,运用博弈论的相关理论,建立以对问题的假设上,探讨集体决策与投票的合理性。同时,通过假设验证的探讨,本文进一步的结合人事管理的相关观点,回归讨论人事管理中的集体决策逻辑。
1 部门利益与博弈假设
假设一:以利益相关的各个部门代表参加下的集体决策与投票,得出的结果可能是最优的,也可能是最差的。
假定组织的某项决策是由相关的各个部门代表集体决定或者投票产生与通过,而且假定决策通过才能使组织的利益实现最大化。在部门利益最大化的前提下,部门不会以组织利益最大化进行活动,而是每个部门代表都会选择自身利益最大化或者是最优的决策选择。也就是说,在部门利益最大化的条件下,每个部门代表的选择不是基于对问题选项的科学分析和理性思考,而是建立在追求自身部门利益最大化的博弈过程。一项决策的产生,可能是A部门所希望,也可能是B部门所希望的,但是可能C部门与D部门反对这项决策,或者希望修改其中的一些条件才会支持这项决策,而C部门与D部门各自所希望修改的条件会产生冲突。这样的背景下(在这里暂且不讨论串通结盟的情况),按照少数服从多数的原则,这项决策可能会有几个结果,如表1所示。
由表1可以看出,无论部门之间做出如何的选择或投票,决策过程中集体需要面对的选择组合至少有20种,而无论组合与组合之间如何进行选择,最终都只能在4种决策结果中进行选择。为了简化讨论上述的结果分布,以便更加明了的对假设一的检验。下面将通过只有A和C两个变量的囚徒困境对上述的政策结果做进一步的简化,如图1所示。
由图1可以看出,对变量的简化并没有影响决策的结果分布。这里依然有通过、妥协支持、妥协反对、反对这四种决策结果。因此,在假设下,无论利益部门如何追求实现自身利益的最优结果,以及组织决策过程中利益部门的多寡,只要存在利益矛盾或者利益不一致性,决策结果都至少会损害到其中一方的利益。
假设二:以利益相关的各个部门和其他利益无关部门共同代表参加下的集体决策与投票,决策均衡点会随着噪音的影响而产生变动。
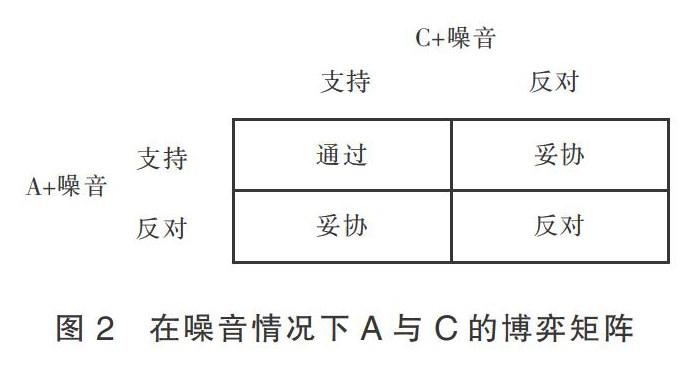
为了论述加入其他部门这一情况对集体决策与投票的影响,继续以上述的博弈矩阵为例。在没有其他部门这一噪音的情况下,得出利益相关部门的博弈矩阵,如图1所示。假定在完全信息动态的条件下,其他部门会受到利益相关部门的信息干扰,即通常所说的串通结盟或者利益收买,那么,作为一种噪音,其他部门的选择就会对集体决策与投票的结果产生影响,如图2所示。
在前面的假设一中,组织决策效用是一条由不同决策支持比组成的曲线。加入其他部门这一噪音后,不同决策支持比所产生的效用会应噪音的依附而产生相应的变化。由于不知道假设一中效用函数的具体形式,在这里用组织决策的收益曲线来代替说明在噪音影响下决策均衡点的变动情况,如图3所示。
图3中,曲线a是没有噪音情况下的政策收益函数,曲线b和曲线c是加入噪音情况下的政策收益函数。由于噪音的选择会可能倾向A的选择,也可能是倾向B的选择,也可能是在两者之间分布,这取决于双方的博弈过程,因此,这就产生了不同于曲线a的两条收益曲线b和c。但对于组织者来说,决策的最高收益是不变的,即曲线a的最高点,因此,曲线b和c的最高点是和曲线a一致的,均衡点的变动在于决策支持比之间的博弈。但对于组织者来说,此时决策的最高收益并不定在曲线b或者曲线c的最高点上,因为决策支持比的选择是众多的,也有可能是分散的,因此概率最大的收益点应该是在曲线b与c的交点上。
假设三:以利益无关的各个部门共同代表参加下的集体决策与投票,得出的结果可能会是最差的。
假定在组织的决策需要各个部门的参与讨论与决策才能得出组织利益最优化的方案,然而由于与个人部门利益无关,利益无关的各个部门必然会选择冷漠或者尽量避免参与决策所带来的成本损失。在这一前提下,假设有n个利益无关的部门要求参与集体决策与投票。每个组织的代表都希望能够为组织的决策做出贡献,但是他们都偏好别人去参与决策(因为去参与组织的决策可能要付出成本,比如,需要放弃部门的工作或者个人的闲暇、其他机会成本等)。如果没有人愿意参与组织的决策,那么自己去参与,总比受到来自组织的批评与给与的压力要好。具体来说,无关部门之间的博弈如下:
(1)参与者集合:n个部门,N={1,…,n}
(2)策略空间:Si={C,D},C代表参与讨论提议与决策,D表示不参与讨论提议与决策,i=N。
(3)偏好:对于第i个参与者,如果别人提出决策意见而自己不提议,收益为v;如果自己提出提议那么收益就为v-c>0;如果没有任何代表提议,那么组织的收益就为0。
假设每个代表提议的概率都为1>P>0,那么1-P就是不提议的概率,因而混合策略(假设二情况下的噪音选择)为(P,1-P)。如果参与者运用混合策略,那么概率为正的纯策略下的期望值都应该相等。如果第i个代表提出提议,那么他的收益为v-c;如果他没有提议,那么就会有两种情况:一种是没有代表提议,另一种是至少有一个代表参与决策讨论与提议。因而对于组织而言,集体决策与投票的期望值为
0×Pr{没有代表提议}+v×Pr{至少有一个代表提议}。
在均衡条件下必有v-c=0×Pr{没有代表提议}+v×Pr{至少有一个代表提议},此时没有代表提议的概率为Pr=1-Pr,将其代入上式可得v-c=1-Pr。根据已知条件,Pr=(1-P)n-1,由此得P=1-(c/v)1/(n-1)。
进一步,由于该博弈存在唯一一个混合纳什均衡,因此:
Pr{没有代表提议}= Pr{出席会议的代表i没有提议}×Pr{其他代表没有提议}。
对上式关于n求导,得
即随着出席会议的代表数增加,没有代表提议的概率是增加的,由于至少有一个代表提议的概率等于1减去没有代表提议的概率,因而出席会议的代表越多就越有可能出现所有代表都不提议的情况。由于存在这多个不同利益部门的代表,任意一个代表不提议的概率为(c/v)1/(n-1),同时由于c/v<1,当n增加时,不提议的概率(c/v)1/(n-1)会变大,原因在于利益无关的各个部门产生了相互依赖或者侥幸的心理,总是寄希望于其他部门参与集体提议与讨论。虽然每个部门都希望组织的利益能够实现最大化,但是又存在这一点点私心,最终就会可能出现最差的结果。
2 结果与讨论
(1) 基于假定条件下的以利益相关的各个部门代表参加下的集体决策与投票,可以得出最优的结果,也可以得出最差的结果。
在假定的条件下,多部门参与的决策与投票的选择至少有20种,即使在简化了的只有两个利益部门的囚徒困境矩阵中,组织依然要面对通过、妥协支持、妥协反对、反对这四种利益部门决策结果的选择博弈,同时还要寄希望于部门之间的博弈刚好落在效用最高点上,这样才能使得整个组织的收益是最大的。但是效用最高点只有一个,也就是说,组织效用能搞实现最大化的至少概率为1/4,实现收益最大化的概率随着利益部门的增多而变小(假定条件下没有简化前的多部门博弈收益最大化的概率为1/20)。虽然在实际情况中,假设一下的诸多假设可能是不成立的,但是在部门利益最大化的条件下,每个部门代表的选择不是基于对问题选项的科学分析和理性思考,而是建立在追求自身部门利益最大化的博弈过程。因此,现实中不会只存在一种结果,使得组织的效用实现最优,即组织的效用依然是一条由各种结果组成的曲线。
(2) 以利益相关的各个部门和其他利益无关部门共同代表参加下的集体决策与投票,决策均衡点下的组织收益水平往往比没有噪音的条件下更低。
在假设二的条件下,由于有利益无关的其他部门加入到组织的集体决策与投票中来,组织的收益函数由曲线a更变为曲线b和曲线c。相对于假设一的情况来说,此时组织的组织效用能搞实现最大化的概率将会更低。因此,对于组织来说,噪音的增加使得组织获得更高收益的概率会更低。因为决策支持比的选择由于噪音的干扰将会变得更多更分散,因此概率最大的收益点应该是在曲线b与c的交点上。
(3) 由于冷漠与自私自利的存在,以利益无关的各个部门共同代表参加下的集体决策与投票,得出的结果并不会是组织所想要的。
在假设三的模型中,由于至少有一个代表提议的概率等于1减去没有代表提议的概率,因而出席会议的代表越多就越有可能出现所有代表都不提议的情况。实际上如果只有一个部门出席参与决策,那么决策提议的概率是1,但是事实上由于存在这多个不同利益部门的代表,任意一个代表不提议的概率为(c/v)1/(n-1),同时由于c/v<1,当n增加时,不提议的概率(c/v)1/(n-1)就会变大,因此集体决策与投票最终就会可能出现最差的结果。
上述的结果是建立在理想的假设条件下得出的,是对现实问题进行修补性或者说是有条件限制的探讨,从特定的范围内验证现实问题的运行逻辑。因此,结果的得出是有赖于建立在理想的假定条件,而理想的假定条件在实际环境中是特殊的存在着,因为假设中的条件在现实运行中是很难达到的,比如假设一中对决策通过才能使组织的利益实现最大化的假定。现实中也可能会出现会议操纵或者议程既定、利益部门的惯性思维等情况,而且,在实际中,信息的非完全性与传递的不可测量或者完全信息静态下的博弈会降低对结果的可信度。
参考文献:
[1] NASH J. Equilibrium points in n-person games[J]. Proceeding of the National Academy of Sciences of the United of America,1950,36:48-49.
[2] NASH J. Non?鄄cooperative games[J]. Annals of Mathematics,1951,54:286-295.
[3] 姚国庆. 博弈论[M]. 北京:高等教育出版社,2007.
[4] 帕特里克·麦克纳. 公共选择经济学[M]. 长春:长春出版社,2008.
[5] 戈登·塔洛克. 论投票——一个公共选择的分析[M]. 成都:西南财经大学出版社,2007.
[6] 奥尔森. 集体行动的逻辑[M]. 上海:上海三联书店,1990.
[7] 宗计川. 公共选择理论框架下投票出席行为论述[J]. 中国行政管理,2013(1):117-120.
[8] 毕文君. 从投票规则体制的视野反思教育决策民主性[J]. 法治与社会,2008(6):231-232.
[9] 刘长发. 关于部门利益的若干理论思考[J]. 四川行政学院学报,2005(6):5-8.
[10] 何丽华. 协商民主与票决民主的必要结合——当代集体决策的现实选择[J]. 贵州社会主义学院学报,2010(4):39-42.
(责任编辑:徐兴华)
