强化学习方法的对比分析
2015-04-29栾咏红章鹏
栾咏红 章鹏

摘 要: 强化学习是指从环境状态到行为映射的学习,使智能体从环境交互中获得的累积奖赏最大化。文章在介绍强化学习原理和方法的基础上,对动态规划、蒙特卡罗算法和时间差分算法进行了分析,并以栅格问题为仿真实验平台进行算法验证,分析比较了蒙特卡罗算法与时间差分算法学习速率的收敛性,以及学习率对时间差分算法的影响。实验结果表明,时间差分算法收敛速度比蒙特卡罗算法快一些;学习率选取较大时,时间差分算法收敛速度会快一些。
关键词: 强化学习; 动态规划; 蒙特卡罗方法; 时间差分方法; 值函数
中图分类号:TP18 文献标志码:A 文章编号:1006-8228(2015)12-93-05
Comparative analysis of reinforcement learning method
Luan Yonghong1,2, Zhang Peng2
(1. Suzhou Institute of Industrial Technology, Suzhou, Jiangsu 215104, China; 2. Institute of Computer Science and Technology, Soochow University)
Abstract: Reinforcement learning is the learning from environment state mapping to action, to maximize the accumulated reward from the interaction with the environment. On the basis of the introduction of principles and methods of reinforcement learning, the dynamic programming, Monte Carlo algorithm and temporal-difference algorithm are analyzed, and the gridworld problem is used as the experiment platform to verify these algorithms. The convergence comparison between Monte Carlo algorithm and temporal-difference algorithm and the effect of the learning rate on the temporal-difference algorithm is analyzed. The analysis of the experiment result shows that temporal-difference algorithm is found to converge faster than Monte Carlo algorithm. The increase of learning rate improves the convergence rate of temporal-difference algorithm.
Key words: reinforcement learning; dynamic programming; Monte Carlo methods; temporal-difference method; value function
0 引言
強化学习(reinforcement learning:RL)又称为增强学习或再励学习,是一种从环境空间状态到动作空间映射的学习,通过试错法不断与环境交互,期望动作从中获得的累积奖赏值最大[1,7,8],它是以环境反馈作为输入的机器学习方法,也是近年来自动控制和人工智能领域的研究热点之一。
1 强化学习理论
1.1 强化学习基本原理
强化学习是基于动物学习心理学的“试错法”原理,智能体在与环境交互的过程中根据评价性反馈信号实现从环境状态到动作状态的学习,使得行为策略能够从环境中得到最大的累积奖赏值,最终收敛到最优策略,实现马尔科夫决策过程的优化,解决了优化控制问题[2,6,7,8]。
在强化学习过程中,智能体的任务就是学习获得一个最优控制策略π*:S→A(其中S状态集,A为动作集)。也就是找到一个从状态到动作的映射,以得到最大化期望奖赏值的总和。强化学习框架模型如图1所示。
在策略π*:S→A指导下,智能体与外界环境不断进行试探交互,根据策略智能体选择动作a作用于环境,该环境接受动作后产生一个强化信号r反馈给智能体,然后智能体再根据强化信号正负和当前状态的策略选择下一个动作。如果智能体与外界环境交互接受的强化信号为正,则为奖赏信号。这个奖赏信号通常是一个标量,它反映了某一时刻动作所作出的即时评价,也就是立即奖赏。由于选择的动作不仅影响立即奖赏值,而且还影响智能体迁移到的下一状态以及最终奖赏回报。因此,智能体选取动作时,其原则是要能够获得环境最大的奖赏。
[Agent][环境] [奖赏r][状态s] [动作a]
图1 强化学习模型
定义1 在t时刻,从任意初始状态st起按照任一策略π选择动作,从环境中获得的累积值称为累积回报,用Vπ(st)表示。则状态值函数Vπ(st)定义形式[7]如式⑴。
⑴
式⑴为无限水平折扣模型,智能体仅仅考虑未来获得的期望回报,并以某种形式的折扣累积在值函数中,其中rt是智能体从st到st+1所获得的立即回报,γ称为折扣因子,是用来确定长期回报和立即回报的相对比例,反映了学习系统对未来回报的重视度。γ取值越小,表示越重视短期回报,当γ取值为0时,表示只看重下一时刻的回报;当γ取值越大,表示重视长期回报,当γ取值为1时,表示对未来的所有回报是同等对待的。
策略的優劣是通过状态值函数进行判断的,故最优状态值函数对应的就是最优策略。由方程最优性原理知最优状态值函数为
⑵
所求得的最优策略可以表示为
⑶
1.2 马尔科夫决策过程
通常假定环境是马尔科夫型的,将满足马尔可夫性质的强化学习任务称为马尔可夫决策过程[1,3,4,7](Markov Decision Process,MDP)。强化学习的研究主要集中于马尔科夫问题的处理。
定义2 (马尔可夫决策过程MDP)设存在一个四元组
MDP本质[1,5,7,8]是:当前状态向下一状态迁移的概率和所获得的奖赏值仅仅取决于当前状态和选择的动作,而与历史状态和历史动作无关。因此在已知状态转移概率函数T和奖赏函数R的环境模型下,一般采用动态规划技术求解最优策略。而强化学习着重研究在T函数和R函数未知的情况下,智能体如何获得最优动作策略。这就需要智能体通过试探,从环境中获得立即回报从而学习状态值函数。在试探过程中,智能体为了获得环境的立即回报,必须采取一定的动作来改变当前的环境状态。
强化学习系统中常用动作选择机制有ε-greedy贪婪机制和Boltzmann分布机制。ε-greedy动作选择机制是优先按概率1-ε(0?ε<1)选择使动作值最大的动作,当该动作未被选中时,则以概率ε选择动作集A中其他动作执行。Boltzmann分布动作选择机制,是按照每个动作值的大小来给该动作赋予一个选择概率。
2 强化学习的基本方法
解决强化学习问题的基本方法有动态规划方法、蒙特卡罗方法和时间差分学习方法。这些方法都能很好的解决强化学习中存在的一系列问题。但是近年来对强化学习算法的研究已由算法本身逐渐转向研究经典算法在各种复杂环境中的应用,如Q学习算法,Sarsa算法,Dyan算法等。
2.1 动态规划
动态规划(Dynamic Programming,DP)是由Bellman于1957年提出,并证明了动态规划方法可以用来解决很广泛的问题。动态规划其主要思想是利用状态值函数搜索好的策略,在文献[1]中都证明了动态规划方法就是利用值函数来搜索好的策略。
动态规划方法是由Bellman方程转化而来,通过修正Bellman方程的规则,提高所期望值函数的近似值。常用算法有两种:值迭代(Value Iteration)和策略迭代(Policy Iteration)。
假设环境是一个有限马尔可夫集,对任意策略π,如果环境的动态信息已知,即策略π、T函数和R函数已知,可以用值迭代法来近似求解。则状态值函数更新规则如式⑷。
⑷
在任意策略π下的任意状态值函数V满足Bellman方程的式⑴与式⑷两种形式。值迭代算法就是将Bellman方程转换成更新规则,利用Bellman方程求解MDP中所有状态值函数。则状态值函数V'(s)满足Bellman最优方程,表示为:
⑸
由于值迭代算法直接用可能转到的下一步s'的V(s')来更新当前的V(s),所以算法不需要存储策略π。值迭代是在保证算法收敛的情况下,缩短策略估计的过程,每次迭代只扫描(sweep)了每个状态一次。而策略迭代算法包含了一个策略估计的过程,而策略估计则需要扫描(sweep)所有的状态若干次,其中巨大的计算量直接影响了策略迭代算法的效率。所以说,不管采用动态规划中的哪种算法方法都要用到两个步骤:策略估计和策略改进。
动态规划方法通过反复扫描整个状态空间,对每个状态产生可能迁移的分布,然后利用每个状态的迁移分布,计算出更新值,并更新该状态的估计值,所以计算量需求会随状态变量数目增加而呈指数级增长,从而造成“维数灾”问题[4,7.8]。
2.2 蒙特卡罗方法
蒙特卡罗方法(Monte Carlo methods:MC)是一种模型无关(model free)的,解决基于平均样本回报的强化学习问题的学习方法[7-8]。它用于情节式任务(episode task),不需要知道环境状态转移概率函数T和奖赏函数R,只需要智能体与环境从模拟交互过程中获得的状态、动作、奖赏的样本数据序列,由此找出最优策略。MC方法具有一个很重要的优点就是该方法对环境是否符合马尔可夫属性要求不高。
假定存在终止状态,任何策略都以概率1到达终止状态,而且是在有限时间步内到达目标。MC方法通过与环境交互过程中来评估值函数的,从而发现最优(较优)策略的。MC方法总是通过平均化采样回报来解决强化学习问题。正是由于MC方法的这个特点,要求要解决的问题必须是可以分解成情节(episode)。而MC算法的状态值函数更新规则为:
⑹
其中Rt为t时刻的奖赏值,α为步长参数(0<α<1)。MC算法只有在每个学习情节到达终止状态并获得回报值时才能更新当前状态的值函数。所以相对那些学习情节中包含较多步数的任务,对比TD算法,MC算法的学习速度就非常慢。这也是MC算法的一个主要缺点。
2.3 时间差分学习方法
时间差分(Temporal-Difference,TD)学习方法是一种模型无关的算法,它是蒙特卡罗思想和动态规划思想的结合,一方面可以直接从智能体的经验中学习,建立环境的动态信息模型,不必等到最终输出结果产生之后,再修改历史经验,而是在学习过程中不断逐步修改。正因为这个特点使得TD方法处理离散序列有很大的优势[1,4,6,7]。另一方面TD方法和动态规划一样,可以用估计的值函数进行迭代。
最简单的TD方法为TD(0)算法,这是一种自适应的策略迭代算法。文献[1]指出TD(0)算法是由Sutton在1988年提出的,并且证明了当系统满足马尔科夫属性,α绝对递减条件下,TD算法必然收敛。TD(0)算法是指智能体获得立即回报值仅向后退一步,也就是说迭代仅仅修改了相邻状态的估计值,则TD(0)算法的值函数更新规则为:
⑺
其中α称为学习因子或学习率(也称为步长参数,0<α<1),γ称为折扣因子(0?γ?1)。由于TD(0)算法利用智能体获得即时回报值,修改相邻状态值函数估计值,因此会出现收敛速度慢的情况。Singh等人对TD(0)算法进行改进,将智能体获得的立即奖赏值由仅回退一步扩展到可以回退任意步,形成了TD(λ)算法。
TD(λ)算法比TD(0)算法具有更好的泛化性能,0?λ?1是资格迹的衰减系数。TD(λ)算法是一个经典的函数估计方法,每一个时间步的计算复杂度为Q(n),其中n为状态特征的个数。当学习因子α或者资格跟踪参数λ选得不合适时,TD(λ)甚至会发散的。
3 基于栅格问题仿真实验
3.1 栅格模型
柵格问题是一类经典的人工智能问题,常被用来验证强化学习算法的有效性。一般用二维网格世界来描述,每个网格代表智能体的一种状态。S表示开始状态,G表示终止状态。智能体的任务是从起始点出发,寻找一条最优的路径,到达终点处。智能体在任意状态下能执行的动作有向上、向下,向左和向右。如果移动后的状态是边界,智能体状态保持不变,否则执行动作后智能体将迁移到相应的邻近状态。智能体到达目标状态前的每一步状态迁移的立即奖赏均为r=0,迁移到目标状态G的立即奖赏r=1。
实验主要关注状态空间维度分别为5×5和20×20两种情况,含三个方面的内容:①智能体通过学习获得的最短路径轨迹;②在相同的学习因子,智能体在MC算法与TD算法下学习过程的收敛情况;③若学习率α的取值不同,TD算法值函数估计误差的比较以及算法的收敛情况。
本文实验选用ε-greedy贪婪机制选取动作,设置ε=0.1,选取动作时选择最大动作值对应的动作概率为1-ε=0.9,选择其他动作概率为ε=0.1。折扣因子γ(0?γ?1)反映了学习系统对未来回报的重视度。实验中学习算法的参数设置为:探索因子ε=0.1,折扣因子γ=0.9,学习率α=0.1。
[\&\&\&\&\&\&\&\&G\&\&\&\&\&\&\&\&\&\&\&\&S\&\&\&\&\&]
图2 栅格问题示意图
3.2 实验结果与算法收敛分析
在MDP环境模型已知的情况下,使用动态规划的值迭代算法更新求解最优策略。根据已知模型先验知识进行初始化,实验时采用贪心策略的状态值函数估计,根据式⑺动态规划值迭代更新规则计算值函数,每一次迭代过程中更新所有状态的值,在值迭代过程中不断逼近最优值,当所有状态的值函数的更新误差Δ小于设定的阈值ε=0.005时,值迭代算法收敛。
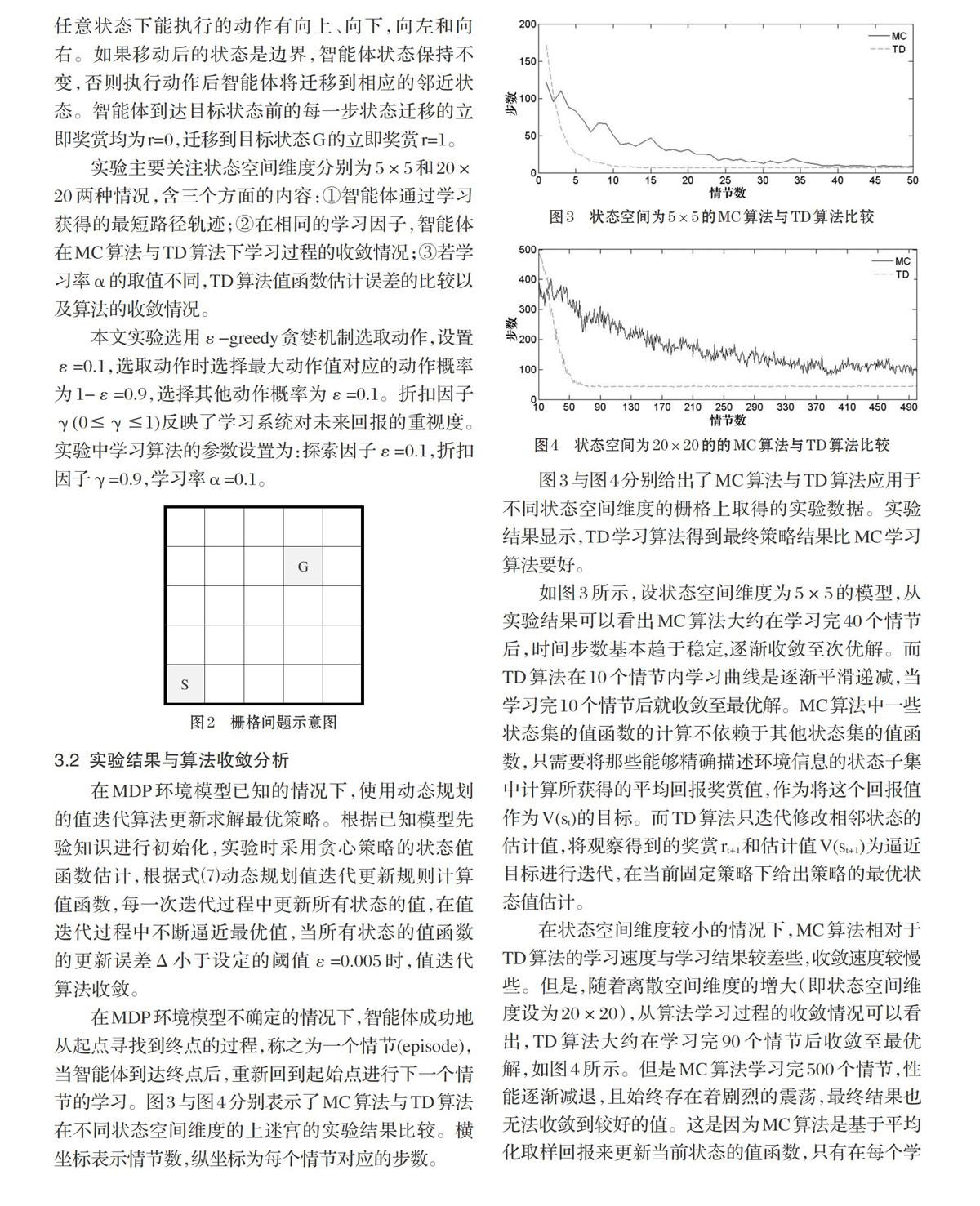
在MDP环境模型不确定的情况下,智能体成功地从起点寻找到终点的过程,称之为一个情节(episode),当智能体到达终点后,重新回到起始点进行下一个情节的学习。图3与图4分别表示了MC算法与TD算法在不同状态空间维度的上迷宫的实验结果比较。横坐标表示情节数,纵坐标为每个情节对应的步数。
图3与图4分别给出了MC算法与TD算法应用于不同状态空间维度的栅格上取得的实验数据。实验结果显示,TD学习算法得到最终策略结果比MC学习算法要好。
如图3所示,设状态空间维度为5×5的模型,从实验结果可以看出MC算法大约在学习完40个情节后,时间步数基本趋于稳定,逐渐收敛至次优解。而TD算法在10个情节内学习曲线是逐渐平滑递减,当学习完10个情节后就收敛至最优解。MC算法中一些状态集的值函数的计算不依赖于其他状态集的值函数,只需要将那些能够精确描述环境信息的状态子集中计算所获得的平均回报奖赏值,作为将这个回报值作为V(st)的目标。而TD算法只迭代修改相邻状态的估计值,将观察得到的奖赏rt+1和估计值V(st+1)为逼近目标进行迭代,在当前固定策略下给出策略的最优状态值估计。
在状态空间维度较小的情况下,MC算法相对于TD算法的学习速度与学习结果较差些,收敛速度较慢些。但是,随着离散空间维度的增大(即状态空间维度设为20×20),从算法学习过程的收敛情况可以看出,TD算法大约在学习完90个情节后收敛至最优解,如图4所示。但是MC算法学习完500个情节,性能逐渐减退,且始终存在着剧烈的震荡,最终结果也无法收敛到较好的值。这是因为MC算法是基于平均化取样回报来更新当前状态的值函数,只有在每个学习情节到达终止状态并获得返回值时,才能更新当前状态的值函数。在大空间状态下批量更新,MC算法由于采样一次学习所获得的立即奖赏值,然后多次学习逼近真实的状态值函数,而每次学习必须要等到当前情节(episode)终止时才能够进行。MC算法得到的是训练样本集上具有最小均方差的估计值。而TD算法不必等到最终输出结果产生之后再修改以往学到的经验,而是在学习过程中逐步修改。TD算法得到的估计值是马尔科夫过程最大似然模型得到的精确值。因此,TD算法比MC算法收敛更快。
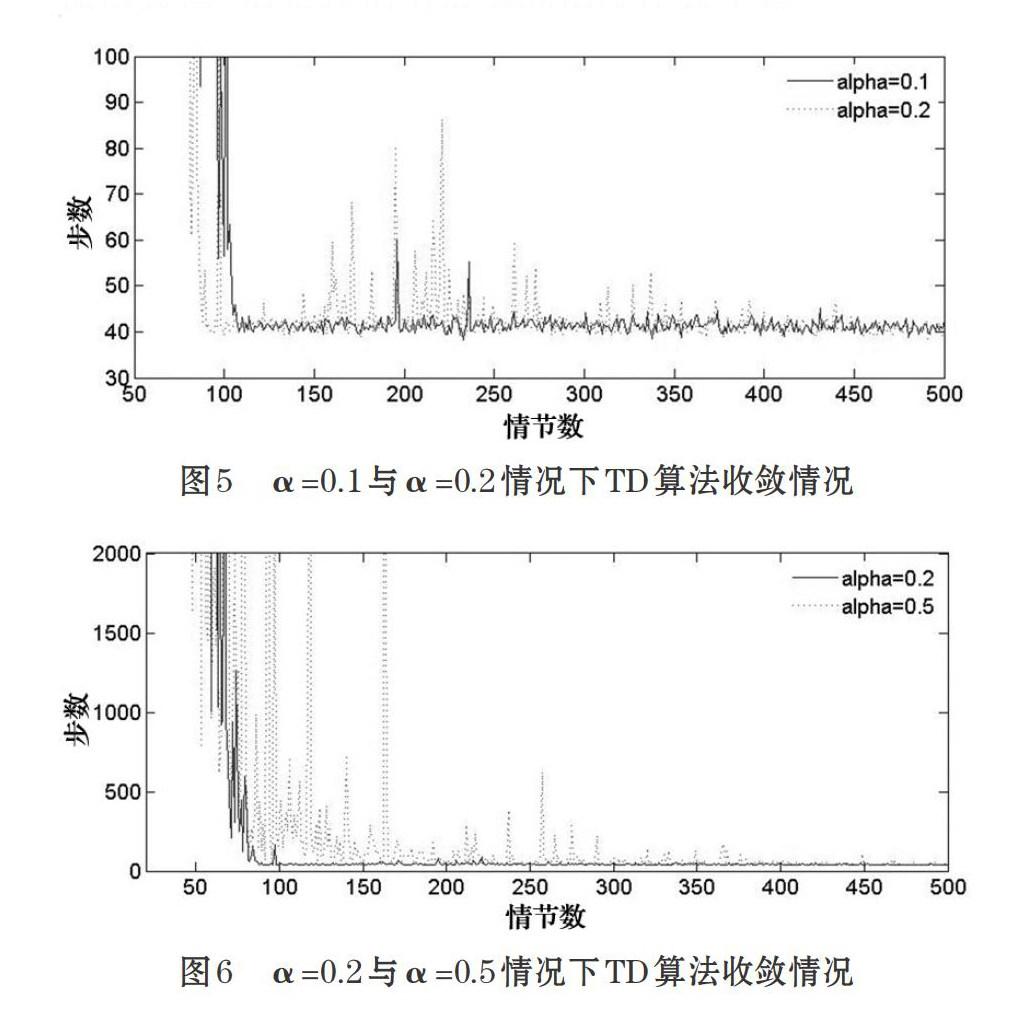
Sutton在1988年提出并证明了TD(0)算法的收敛性,即TD(0)算法在最小化均方差(Mean Square Error:MSE)意义下的收敛性。虽然存在收敛速度慢的问题。但是当系统满足马尔科夫属性,学习因子α绝对递减条件下,TD(0)算法必然收敛。图5和图6分别给出了学习因子α取值不同时,TD学习速度收敛的情况。实验中TD算法根据ε-greedy贪心策略确定动作,探索因子ε=0.1, 折扣因子γ=0.9,学习因子分别设为α=0.1,α=0.2,α=0.5。在状态空间维度20×20的迷宫模型验证。从实验结果可以看出,选取较大的α值时,TD算法能够较快收敛,但是不够平稳,需要较长时间才能平稳;选取较小的α值时,TD算法收敛速度较慢,但是在情节数多的情况比较平稳。
4 结束语
基于查询值表(Lookup-table)的TD方法是强化学习中一個经典的值函数预测方法,即只评估某个稳定策略下的值函数,解决了强化学习中根据时间序列进行预测的问题。
离散的马尔可夫决策过程是强化学习研究的重要理论基础,已知状态转移概率T和奖赏函数R的前提下,可以采用动态规划的值迭代过程得到最优策略。
动态规划中的值迭代算法是通过在各种策略下计算状态值函数,找出最优状态值对应的最优策略。但是,这种方法每次迭代计算相对简单、计算量小,但是所需的迭代次数可能较大。
MC方法是从样本情节形式的经验中学习值函数和逼近最优策略,解决基于平均样本回报的强化学习问题的方法。
本文主要是针对小规模的、离散状态空间问题,分析比较了MC算法与TD算法的收敛性。近年来,基于值函数逼近的强化学习方法越来越多地被用于模式识别、工业制造等领域,具有大规模连续动作空间的强化学习问题成为研究的热点。这也是下一阶段学习和研究的任务。
参考文献(References):
[1] Sutton R S, Barto A G. Reinforcement learning: An
introduction[M]. Cambridge: MIT Press,1998.
[2] Busoniu L, Babuska R, De Schutter B, et al. Reinforcement
learning and dynamic programming using function approximators[M]. USA: CRC Press,2010.
[3] 高阳,陈世福,陆鑫.强化学习研究综述[J].自动化学报,
2004.33(1):86-99
[4] Kaelbing L p, Littman M l, Moore A W. Reinforcement
learning: a survery[J]. Journal of Artificial Intelligence Rearch,1996.4:237-285
[5] Ratitch B. On characteristics of Markov decision processes
and reinforcement learning in large domains[D]. PhD thesis, The School of Computer Science McGill University,Montreal,2005.
[6] Konidaris G. A framework for transfer in reinforcement
learning[C]. In:ICML-2006 Workshop on Structural Knowledge Transfer for Machine Learning,2006.
[7] Wiering M, Van Otterlo M. Reinforcement Learning:
state-of-the-Art[M].Heidelberg Berlin: Springer,2012.
[8] 陈学松,杨宜民.强化学习研究综述[J].计算机应用研究,
2010.27(8):2834-2838
