面向企业决策问题的软运筹学方法比较研究——网络分析法与模糊认知地图法

张 凌，乔晓东，朱礼军，张瑞军，吕鹏辉

（1．武汉科技大学管理学院，湖北武汉430081；2．中国科学技术信息研究所，北京100038；3．武汉大学信息管理学院，湖北武汉430072）

管理者或决策者在企业中总是面临各种各样的决策问题，为处理非结构化问题或劣构问题所采用的方法，称之为问题构建方法（PSM），或者称之为软科学方法。

一般来说，运筹学是对实际问题进行优化的科学，而对于那些结构不清楚、目标不明确的问题，也叫“议题”，通常会采用软运筹学方法。相对处理结构化问题和具有明确数学模型问题的硬运筹学而言，软运筹学使用了更多的方法和手段，有些来自于人的灵感和直觉，是具有很强干预性的动态调整自适应方法[1]。软运筹学将人的“心智”与计算机的高性能结合起来。“心智”分为“性智”和“量智”两部分，“性智”是一种从定性的、宏观的角度对总的方面巧妙加以把握的智慧，与经验积累、形象思维有密切关系；“量智”是一种定量的、微观的分析，是概括与推理的智慧，与严格的训练和逻辑思维有密切的联系，它是人们通过科学技术领域的实践与训练得以形成的[2]。因此我们也可以说软运筹学方法是通过定性与定量数据相结合来解决复杂问题的方法。

本文所介绍的网络分析法（Analytic Network Process，ANP）和模糊认知地图法（Fuzzy Cognitive Map，FCM）都属于软运筹学方法，因为这些方法都需要使用者注入自己的理念、经验和偏好，才能真正地被用来解决实际问题。在以往的研究当中，大多是对这两种方法的应用，只有少数研究将这两种软运筹学方法进行了联系。由于这两种软运筹学方法有一定的相似性和差异性，因此本文着重从决策模型的结构构建、生成矩阵的赋值、计算方法等方面对这两种决策方法进行比较，最后通过一个案例对比两种决策方法的分析结果，以方便管理者在不同的决策情境中选择合适的决策方法。

一、ANP与FCM方法概述

1．ANP方法的相关描述

ANP法是美国著名运筹学家Saaty继层次分析法（Analytic Hierarchy Process，AHP）之后提出的又一种决策分析方法。AHP的应用研究已有30多年的历史，它在各行各业中得到了广泛应用，为人们所熟知，而ANP产生较晚，其应用研究在国外还远不如AHP广泛和深入，在国内则更为少见。

与AHP相似，ANP通过定性分析与定量计算相结合，把决策者的主观判断和推理紧密联系起来，对决策者的推理过程进行量化描述，因而可应用于求解多准则、结构复杂且不易量化的决策问题，提供科学的决策依据。卢厚清等人认为，AHP以及ANP都需要使用者注入自己的理念、经验和偏好，可以真正地被用来解决实际问题，这些方法也就是具有柔性的运筹学方法[2]。

然而，ANP将问题分解成许多不同类别的群组，各个群组中包含许多元素，群组与元素彼此相关，使用图形方式分析构成群组（clusters）和元素（element）间的关系与交互影响，形成彼此相关的网状图。ANP是以两个实体之间存在相互作用的双向关联为前提，因而能更准确地描述复杂的实体关系，在具有非线性网络关系的决策问题中，具有较高的应用价值。而常规的AHP将系统划分为层次，只考虑上一层元素对下一层元素的支配和影响，是单向作用关系和简单的递阶层次结构。可以认为传统的AHP法只是ANP法的特例[3]。ANP的典型结构如图1所示：

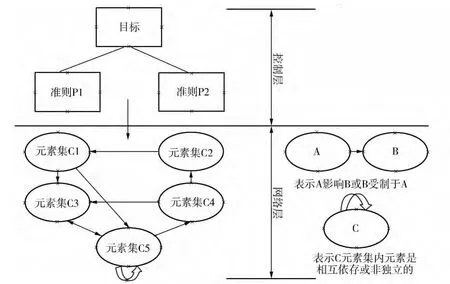
图1 ANP的典型结构[4]

从图1可以看出，所谓ANP的网络是由成分（元素集）以及连接成分之间的影响组成，成分又由组成成分的元素组成，元素之间也可以存在相互影响，一个成分的元素可以与另外一个成分的元素之间发生相互影响关系，各种相互影响关系均用“→”来表示，而“A→B”表示成分（或者元素）A受成分（或者元素）B的影响，或者成分（或者元素）B影响成分（或者元素）A，其中成分本身对自己的影响关系称为反馈关系。ANP中的网络结构用两种形式来表示，一种是图形形式，一种是矩阵形式。图形形式定性地表示组成网络的各个成分之间的相互影响关系以及反馈关系，而矩阵形式定量地表示相互影响或者反馈的程度或者大小[5]。

2．FCM方法

由于FCM属于软科学范畴，像其他的软运筹学方法一样，它所研究的议题有些是本身存在争议的问题，除了使用理性工具中的数学模型，还包括为理清思路引入的概念模型，追求的是满意解或可行且满意的行动方案[6]。在决策过程中，由于采用期望值的方式，所以它不是决策最后的实际益损值，故而与实际情况发生时有一定出入，这就要求决策人还要有一定“主观判断”的能力。目前很多国外学者都利用认知地图软运筹的特点，构造了一些认知模型。

Kwahk K和Kim Y给出了自己创造的模型——两阶段认知模型（Two－phase cognitive modeling，TCM），并且也提供了可以应用于解决实际问题的工具（Two－phase cognitive modeling facility，TCMF）。作者综述了用于解决企业中决策问题的各种不同的认知模型方法和工具，这些模型都使用了认知地图，强调了图形的表示和分析，有些甚至包括评价算法用来计算认知地图的因果强度，有的还介绍了图形的合并或解决各种图的差异问题，同时为解决问题给出评价结果和建议，各类认知模型见表1。

表1中，A－Pool模型是在互联网上基于认知地图的分布型决策过程模型，尽管此模型建议根据一些指标给出决策，然而因果值在分析的时候早已假设给出了[8]；COCOMAP支持群认知的过程以及通过认知映像进行组织学习，它强调了使用加以符号的认知地图作为知识表达方案，而不是问题解决工具[9]；MIND是一个设计用影响图－认知地图来支持复杂企业政治和问题计划的工具，尽管它基于一些衡量算法评估和分析了元素间的路径，然而它不能为解决一个具体问题提供指导并且它使用的是直接尺度值[10]；SODA主要是鼓励组织的成员积极定义他们的策略，通过群体决策，使用COPE软件或者Decision Explorer去获取和管理数据。这个模型有很多应用领域，例如策略发展、组织学习、需求获取等，并且被广大的实践者和学者用于分析定性研究数据以及基于计算机进行群决策，但是它没有给予衡量计算方法即问题解决的指引[11]。TCM模型最初用于支持企业过程重组，通过分析最有效路径和值，尽量通过配对比较使用特征向量方法自动抽取因果值，支持多认知地图聚合。TCM有两个步骤，一是识别因果关系，二是评价每个关系并识别最有效的因果路径。

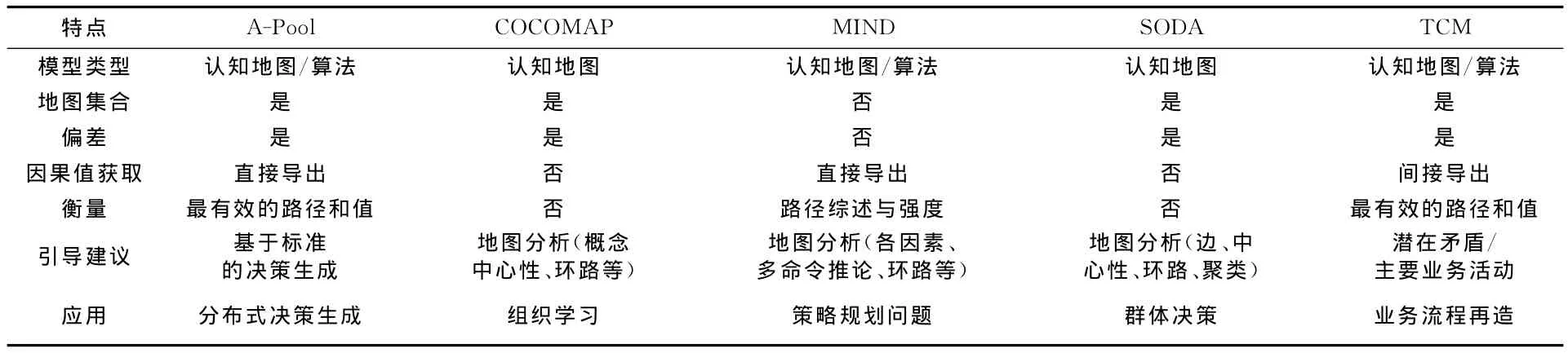
表1 用于企业决策问题的各种不同的认知模型方法和工具[7]

一个认知地图中包括三个部分：因果概念、因果值、因果联系，主要的难点是如何决定因果值，因为它是一个定性的值，反映了参与者的认知地位，不能直接进行估量，而大多数用于认知建模的方法和系统都是使用直接尺度值。然而这些直接的定义方法有很多局限性，使得过程不是系统的，结果很大程度上依赖分析员或者参与者的主观评价。在TCM方法中，特征向量的方法通过成对比较，更加系统化地决定了因果值。

二、ANP与FCM决策方法比较分析

1．ANP和FCM法的相同点

（1）ANP和FCM都是具有柔性的软运筹学方法，都需要使用者注入自己的理念、经验和偏好才能真正地被用来解决问题，都结合定量和定性方法进行决策，都可以通过人们非结构化数据得到结果。人们经常通过头脑风暴法、问卷调查法、面对面访谈等方法收集数据、绘图和权重取值。

ANP是一种通过它的结构来帮助多方达到一个满意的决策结果的技术，如果合理地执行，可以被用于作为一个一致性建构的工具。FCM同样可以收集很多人的思想去构建地图，例如，Scavarda A等给出一个新的方法可以构建一个协作因果图，收集不同人的观点[12]。

（2）人类的思维图式是网状的，ANP和FCM都帮助提升管理理解和模型技术的透明度，人们在思考选择概念和概念之间的关系时，都可以通过网状形式进行表达。一些学者表明，ANP建模过程代替了固定的网络关系所表示的层次标准，还涵盖了元素和聚类的类别之间的关系，所以问题的表达与现实生活更加贴近。因此很多专家认为ANP相比AHP在处理不确定问题和动态决策上更有优势[13－15]。

FCM的主体框架也采用了网状结构，这种网状结构使该模型的环境适应性较强，能够把内部、外部环境的各种影响因素都考虑进来，有利于复杂问题的系统思考和寻求解决策略[16]，而FCM的重要特点就在于它的动态反馈回路。

（3）ANP和FCM都是使用事实构建层次，层次建构对于构建实际中的很多复杂系统是很普遍的方法，是一个对于复杂问题的自然的解决范式。研究发现，ANP中元素之间有线性关系，且允许元素之间有交互关系[17]，如图2所示。为构建一个问题，FCM中的想法概念均是层次上的结构，如目标、关键成功因子、行为（见图3）。

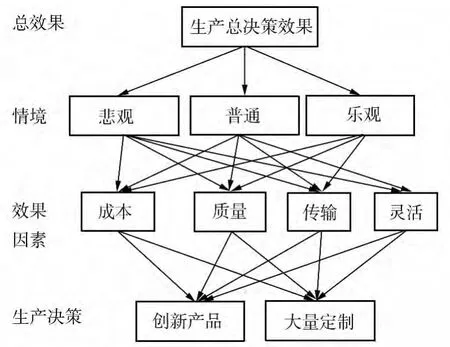
图2 ANP的层次结构

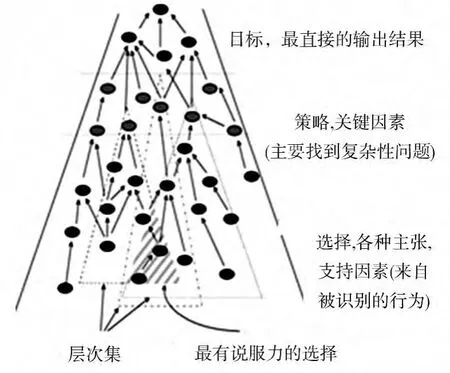
图3 FCM的层次结构

（4）在计算方法上，两种方法都是要构建关系矩阵，在绘制网络结构时，都要为概念之间的关系赋予权重值，权重值代表了网络层次上的指标关系。

2．ANP与FCM法的区别

（1）在矩阵中的赋值上，ANP都是列向量权值相加为1，权重为正数，层次关系明显；FCM列向量的赋值不一定加起来为1，权重有正负，取值属于[－1，1]区间，没有那么明显的层次关系，同时，不像ANP那样，FCM矩阵中对角线向量也不为零。

（2）在ANP中，判断抽取完全采用分解方法，可以减少决策错误。而很多人抱怨在构建FCM过程中没有一个科学的方法去选择概念，FCM依靠初始矩阵得到最终权重结果，错误的初始矩阵或专家错误的评判方法都会导致算法的错误。

（3）ANP和FCM有不同算法，ANP明显的特点是使用超矩阵，但是FCM需要初始加权矩阵和使用人工智能网络算法。

（4）在计算结果上，ANP可以根据目标问题直接计算出所有指标的重要性比重值，可以判断影响度，从而选择最优的方案，而FCM则是根据目标问题，通过迭代算法得出指标的变化从而得出结论，说明指标的影响程度，它并不是一个具体值，这点与ANP不同。

三、案例分析

本文的数据源自Suwignjo[18]和Joseph[19]的论文，他们利用ANP方法对企业单位总成本的影响因素进行分析。ANP结构如图4所示。

图4 单位总成本影响因素及之间的关系

初始矩阵W是节点i到节点j的关系权值，即表2所示影响因素之间的关系；最终的极限超矩阵见表3。

本文采用FCM解决相同的问题，设初始向量A＝（A1＝0．5，A2＝0．5，A3＝0．2，A4＝0．3，A5＝0．3，A6＝0．2，A7＝0．3，A8＝0．3，A9＝0．4，A10＝0．5，A11＝0．2）。将向量A1的值代入FCM迭代公式进行运算：

通过认知地图的推理公式：

经由Matlab编程并计算，可以得到第一次迭代值、第二次迭代值，……，基于此规则进行类推，发现迭代到第五次的时候，达到均衡状态。FCM的迭代过程及均衡状态见表4。

结果表明单位固定成本（FCU）、单位可变成本（VCU）、人员相关成本（PEO）对于目标问题单位总成本（TCU）的影响程度最高，这个结果与使用ANP得到的结果是一样的，但不同之处是利用ANP得到的结论，加班率（OT）对单位总成本的影响程度比FCM得到的结果要大一些，而物资供应成本（MAT）对单位总成本的影响程度相对FCM得到的结论要小一些。

表2 初始矩阵W

表3 最终的极限超矩阵

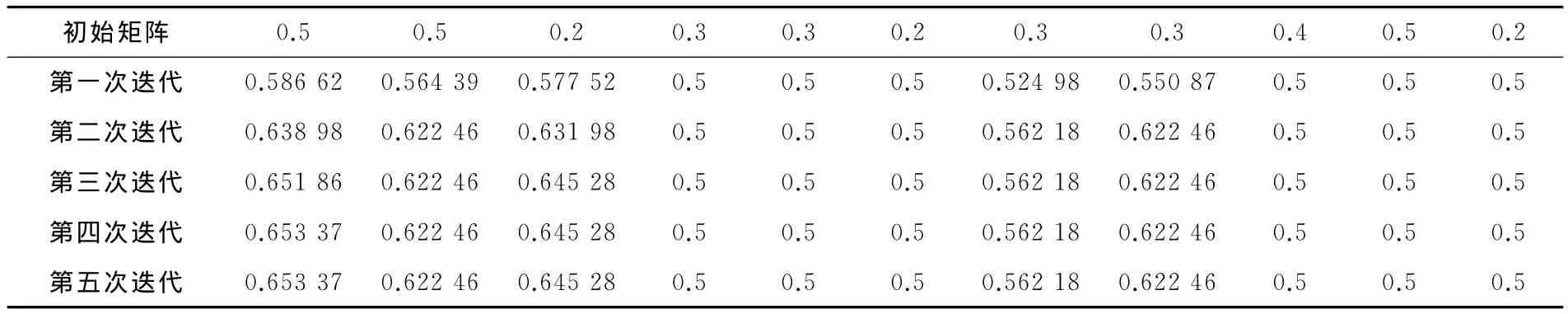
表4 FCM迭代结果

四、结论

本文认为对于企业决策问题，应该因问题特点和情境而选择不同的决策方法，这需要认清ANP与FCM各自的优势和特点，从而选择最优的方案。例如ANP要考虑内部循环相互支配的层次关系，现实中因素间往往存在较复杂的依赖关系和反馈关系，ANP以两个实体之间存在相互作用的双向关联为前提，因而能更准确地描述复杂的实体关系，在具有非线性网络关系的决策问题中具有较高的应用价值。由于网络结构模型远比层次结构模型复杂，因此在权重合成方面，ANP应用到了更加高深的数学知识，其中比较重要的概念是超矩阵的应用和分析。ANP复杂的计算过程可以通过ANP的专门计算机软件Super Decisions实现，得到各个指标的权重。

FCM的建立方便，表现问题直观，能与领域专家头脑中的知识结构形成很好的映射关系，能够自然、直接地表达人类习惯使用的逻辑含义。FCM是一种加权有向图，其理论涉及神经网络、模糊逻辑等。从拓扑结构上看，FCM是一种加权有向图，而加权有向图与神经网络具有很大的相似性，可以看作神经网络的一种形式；另外，它在因果影响关系上引入了模糊测度，从而使FCM这一技术与计算智能有着诸多的结合点，为它的深化研究提供了契机。

[1]于景元，涂元季．从定性到定量综合集成方法——案例研究[J]．系统工程理论与实践，2002，22（5）：127．

[2]卢厚清，蔡志强，贾林枫，等．软运筹学研究的回顾与展望[J]．运筹与管理，2003，12（4）：68－72．

[3]钱政．基于ANP方法的物流网络绩效评价模型[J]．中国集体经济，2008（9）：37－38．

[4]赵国杰，邢小强．ANP法评价区域科技实力的理论与实证分析[J]．系统工程理论与实践，2004（5）：41－45．

[5]唐小丽，冯俊文．ANP原理及其运用展望[J]．统计与决策，2006（12）：138．

[6]李琦．运筹学在系统工程理论中的地位及应用[J]．商场现代化，2008（32）：396．

[7]Kwahk K，Kim Y．Supporting business process redesign using cognitive maps[J]．Decision Support Systems，1999，25（2）：155－178．

[8]W R Zhang，W Wang，R S King．A－Pool：an agent－oriented open system shell for distributed decision process modeling[J]．Journal of Organizational Computing，1994，4（2）：127－154．

[9]S Lee，J F Courtney，R M O’Keefe．A system for organizational learning using cognitive maps[J]．O－mega：The International Journal of Management Science，1992，20（1）：23－36．

[10]A Ramaprasad，E A Poon．A computerized interactive technique for mapping influence diagrams MIND[J]．Strategic Management Journal，1985（6）：377－392．

[11]C Eden，F Ackermann．Strategic options development and analysis SODA—using a computer to help with the management of strategic vision[M]／／G Doukidis，F Land，G Miller．Knowledge－based Management Support Systems．London：Ellis Horwood，1989：198－207．

[12]Scavarda A，Chameeva T，Goldstein S，et al．A methodology for constructing collective causal maps[J]．Decision Sciences，2006，37（2）：263－283．

[13]Saaty T L．Decision making with dependence and feedback：the analytic network process[M]．Pittsburgh：RWS Publication，1996．

[14]Saaty T L．Theory and applications of the analytic network process：decision making with benefits，opportunities，costs，and risks[M]．Pittsburg：RWS Publications，2005．

[15]Saaty T L．Decision making with dependence and feedback：the analytic network process[M]．Pittsburgh：RWS Publications，2001．

[16]马捷，靖继鹏．知识转化模型分析与评价[J]．情报科学，2006，24（3）：359．

[17]Tran L T，Knight C G，O’Neill R V，et al．Integrated environmental assessment of the mid－Atlantic region with analytical network process[J]．Environ Monit Assess，2004，94（1－3）：263－277．

[18]Suwignjo P，Bititci U S，Carrie A S．Quantitative models for performance measurement system[J]．International Journal of Production Economics，2000（64）：231－241．

[19]Joseph Sarkis．Quantitative models for performance measurement systems—alternate considerations[J]．International Journal of Production Economics，2003（86）：81－90．