油液磨粒超声回波信号双树复小波自适应降噪最优分解层数的研究

2015-04-26李一宁张培林徐超杨玉栋张云强吕纯

机床与液压 2015年19期

李一宁，张培林，徐超，杨玉栋，张云强，吕纯

(1．军械工程学院七系，河北石家庄 050003;2．武汉军械士官学校四系，湖北武汉 430075)

0 前言

机械设备在运行过程中，各零部件之间由于相互摩擦会发生磨损，磨损导致润滑油中磨粒逐渐增多［1］，磨粒携带反映机械设备磨损状态的信息。对润滑油磨粒进行检测，能够有效地判断机械设备的磨损状况［2］。随着科技的不断进步，机械设备越来越精密，同时，由于生产要求，一些机械设备需要连续不停机的运行，因此，针对机械设备磨损状态分析的油液磨粒在线检测技术越来越受到人们的重视［3］。

油液磨粒超声在线检测技术相比于其他检测手段，具有检测灵敏度高、穿透力强、费用低等诸多优点［4］，因此，文中采用超声型油液磨粒在线检测技术。在检测过程中，由于测量系统和环境噪声的影响，回波信号被严重污染，尤其是很小的磨粒回波信号，信噪比很低，甚至信号被噪声完全淹没，严重影响设备磨损状态判断，因此，磨粒回波信号降噪十分重要。

目前，信号降噪的方法有很多，如经验模态分解［5-7］、匹配追踪［8］和双树复小波变换［9］等。双树复小波变换是一种新兴的技术，良好的平移不变性和完美重构优于经验模态分解等时频分析方法;有限的冗余性和良好的鲁棒性，使其具有较高的运算效率优于匹配追踪等方法［10］。在双树复小波变换分解过程中，分解层数的选取对于降噪结果尤为重要。因此，本文作者首先基于粒子群优化算法选取最优分解层数，并对最优分解层数选择进行评判，然后将最优分解层数应用到油液磨粒回波信号双树复小波自适应降噪中，结合一种渐近半软阈值函数和一种自适应阈值选取方法，采用信噪比和均方根误差作为判断指标，取得了良好的效果。

1 双树复小波理论

双树复小波变换是新兴的信号处理方法，具有近似平移不变性、良好的鲁棒性等优点，降低了计算的复杂性。双树复小波变换为复小波函数形式，公式如下［11］

双树复小波变换的分解与重构由两颗并行的实小波变换树组成，如图1所示。

图1 双树复小波变换分解与重构过程

2 阈值分析方法

2．1 阈值函数

传统的阈值函数分为硬阈值和软阈值函数2种，硬阈值函数中间不连续，降噪后会出现振荡;软阈值函数降噪后的小波系数与真实值存在误差，降噪结果不准确。针对软阈值和硬阈值函数存在的问题，采用一种渐近半软阈值函数［12］，公式如下:

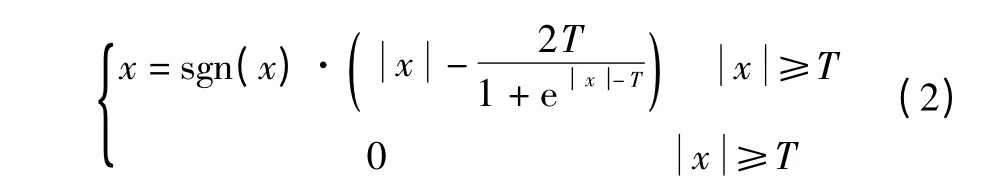
式中:x为小波系数，T为阈值。

文中采用的渐近半软阈值函数与硬阈值函数相比，在T处是连续的，不会产生振荡现象;与软阈值函数相比，随着小波系数的增加，采用渐近半软阈值函数处理后的小波系数逐渐逼近真实小波系数，能够消除小波系数偏差;同时，文中采用的渐近半软阈值函数是高阶可导函数，能够更好地应用于信号降噪中。

2．2 自适应阈值选取方法

阈值的选取直接影响信号降噪的效果，选取的阈值过大，造成有用信息被当成噪声滤掉，选取的过小，信号中包含的噪声不能完全去除。基于以上问题，采用一种自适应的阈值选取方法［13］，该方法选取的阈值能够随着噪声小波系数的变化而自适应的变化，公式如下:

式中:j为分解尺度，阈值T随着分解层数的变化自适应的调整。

3 基于粒子群优化算法的分解层数寻优

3．1 粒子群优化算法

粒子群优化算法的原理为［14］:初始化一个粒子群包含m个粒子，某时刻粒子的位置为Xi=(xi1，xi2，…，xiN)，其速度对应为Vi=(vi1，vi2，…，viN)，粒子经过的最优位置为Pi=(pi1，pi2，…，piN)，粒子群最优位置为Pgbest=(pg1，pg2，…，pgN)，通过式(4)不断更新粒子的速度和位置［15］，求解最优值。

式中:c1、c2为学习因子，ω为惯性权重，r1、r2为(0，1)中的随机量。

3．2 分解层数寻优方法

文中引入粒子群优化算法优化双树复小波自适应降噪分解层数，搜寻最优分解层数，以达到提高降噪效果的目的，分解层数寻优方法的流程图如图2所示。

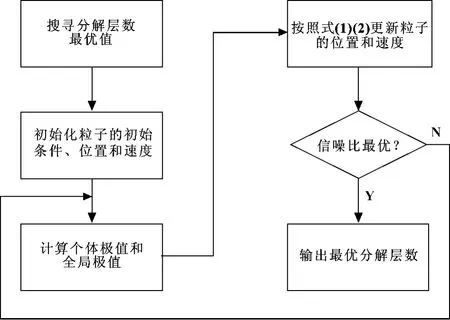
图2 方法流程图

4 仿真分析

为了验证文中提出方法的有效性，采用含噪超声散射回波模型进行仿真分析，首先采用粒子群优化算法求解最优分解层数，对比分析不同分解层数得到的信噪比;然后将最优分解层数代入自适应降噪算法中，利用文中提出的降噪方法对不同信噪比的仿真信号进行降噪;最后对仿真结果进行分析。

文中采用加入高斯白噪声的仿真信号模拟含噪超声回波信号，如图3所示，信噪比(SNR)为10 dB。

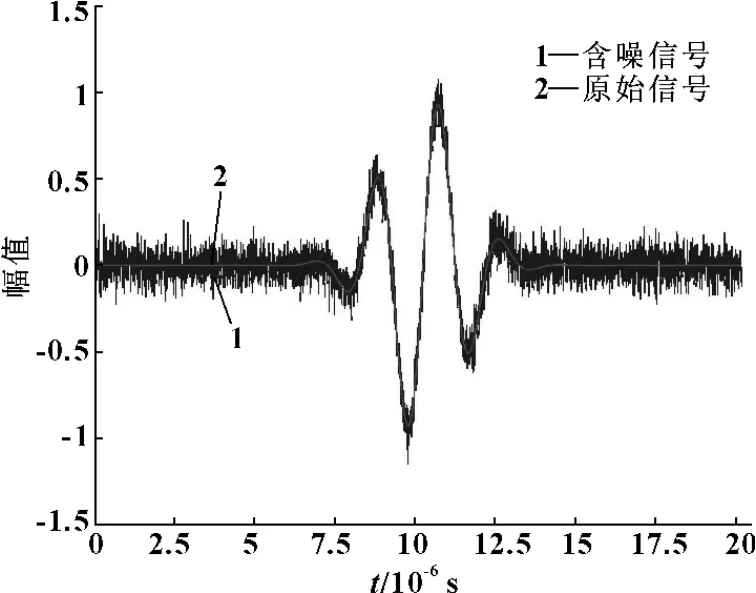
图3 含噪仿真信号

粒子群优化中设置种群数量为50，ωmax=0．9，ωmin=0．4，迭代次数为100，学习因子c1=c2=2。构造适应度函数为降噪后信号的信噪比，公式为:

通过粒子群优化算法寻优得到的最优分解层数如表1所示。

表1 PSO算法获得的最优分解层数

为了进一步验证所求最优分解层数的有效性，选取不同分解层数对磨粒超声回波信号进行降噪，以信噪比为判断指标，得到的信噪比随分解层数变化如图4所示。

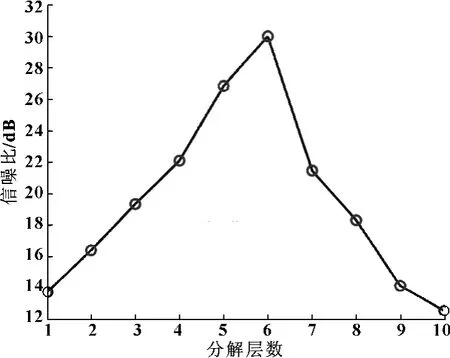
图4 不同分解层数下的信噪比

由图4可以看出，相同的仿真条件下，当分解层数为6层时信噪比最高，因此，通过粒子群优化算法得到的分解层数为最优解。

将最优分解层数代入降噪算法，验证所提出的油液磨粒超声回波信号自适应降噪方法的有效性，文中仿真对象为10组加入不同信噪比高斯白噪声的超声回波信号，并采用信噪比(SNR)和均方根误差(RMSE)作为判断降噪效果的依据。

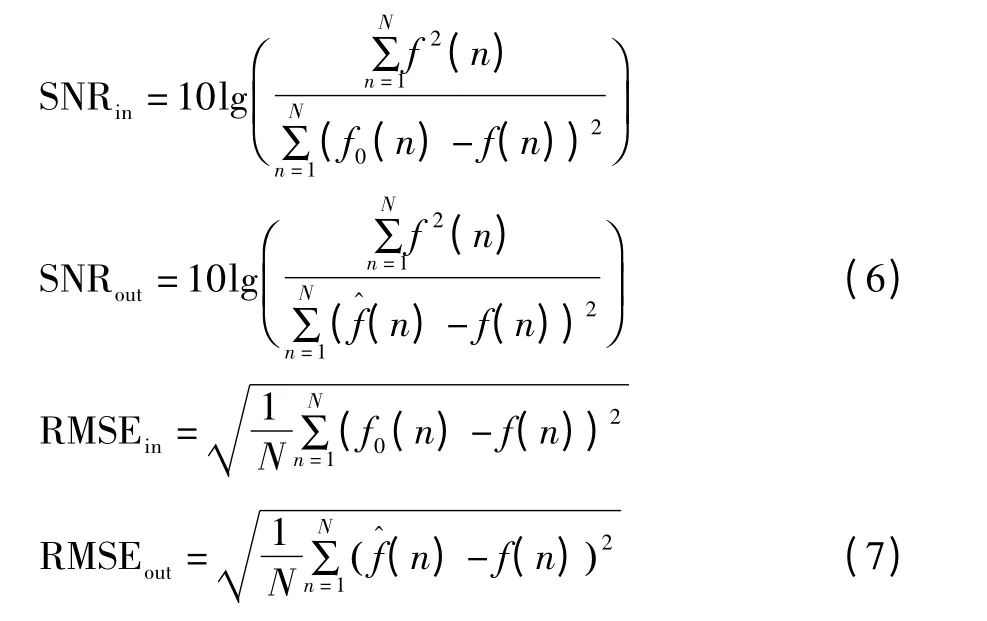
式中:f(n)表示原始信号，f0(n)表示降噪前信号，表示降噪后信号。

经过文中方法降噪后，不同信噪比条件下信号的信噪比和均方根误差如表2所示。由表中的数据可以看出，超声回波信号经过文中方法降噪后，信噪比有较大提高，并且信噪比较低的信号提高较为明显，信噪比提高的平均值达到19．956 1 dB;降噪后信号的均方根误差相对较低，提高了9．941 3倍。表明了文中提出降噪方法的有效性。

表2 10种不同信噪比信号降噪后结果

4 实验分析

为了验证文中通过粒子群优化算法得到的最优分解层数和双树复小波自适应降噪方法在实测超声回波信号中的应用效果。搭建了磨粒超声在线检测实验系统，如图5所示。循环泵将含有磨粒的润滑油从油池中抽出通过超声传感器，检测到的磨粒超声回波信号通过工控机显示并储存。

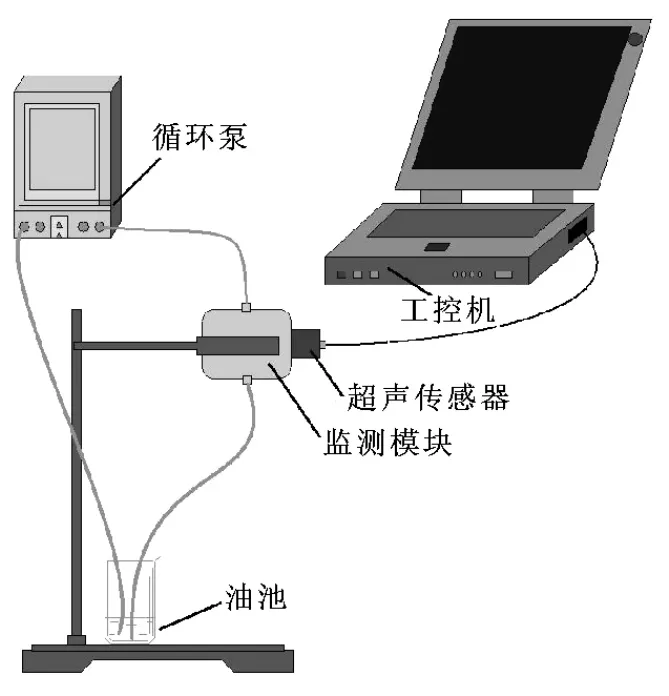
图5 磨粒测试实验系统

当含有磨粒的润滑油通过超声传感器时，磨粒会产生回波信号，回波信号能够反映磨粒的尺寸、形状和材质等信息，同时，机械设备在运行过程中，润滑油会产生大量气泡，区分磨粒与气泡是机械设备磨损状态分析一个十分重要的环节。因此，清晰准确的磨粒回波信号对于机械设备磨损状态监测十分重要。但是在实验过程中，磨粒和气泡的回波信号均被噪声污染，如图6所示。严重影响了后续的信号特征提取与磨损状态分析。

图6 实测磨粒和气泡含噪信号

将粒子群优化算法得到的最优分解层数代入双树复小波自适应降噪方法中，然后对磨粒和气泡回波信号进行降噪处理，结果如图7所示，噪声基本被清除干净，能够还原真实的磨粒和气泡回波信号。

图7 实测磨粒和气泡去噪信号

综上所述，通过粒子群优化算法求解的分解层数最优值结合双树复小波自适应降噪算法能够有效地消除磨粒和气泡回波信号中的噪声，为下一步的信号特征提取与磨损状态分析奠定了基础。

5 结论

基于粒子群优化算法求解得到了最优分解层数为6层，将得到的最优分解层数代入双树复小波自适应降噪算法，降噪效果更佳。仿真与实验分析说明，基于粒子群优化算法求解的最优分解层数信噪比最高，结合最优分解层数的双树复小波自适应降噪算法基本上去除了信号中的噪声，提高了信噪比，降低了均方根误差，还原了真实波形，为下一步的特征提取与磨损状态分析打下了良好基础。

［1］张培林，何忠波，吕建刚，等．车辆结构与原理［M］．北京:国防工业出版社，2007．

［2］明廷锋，朴甲哲，张永祥．磨损颗粒的监测与测量［J］．煤矿机械，2003(11):34-36．

［3］黎琼炜．新型油液在线监控技术［J］．测控技术，2005，24(4):6-10．

［4］明廷锋，朴甲哲，张永祥，等．超声波磨粒监测方法的研究［J］．内燃机学报，2004，22(4):357-362．

［5］王文波，张晓东，汪祥莉．脉冲星信号的经验模态分解模态单元比例的萎缩消噪算法［J］．物理学报，2013，62(6):069701 1-9．

［6］王文波，张晓东，汪祥莉．基于独立成分分析和经验模态分解的混沌信号降噪［J］．物理学报，2013，62(5):050201 1-8．

［7］董烈乾，李振春，刘磊，等．基于经验模态分解的曲波阈值去噪方法［J］．吉林大学学报，2012，42(3):838-844．

［8］李城华，王悦民，朱龙翔，等．改进匹配追踪法在导波检测信号处理中的应用［J］．振动、测试与诊断，2012，32(1):111-115．

［9］王芳，季忠，彭承琳．基于双树复小波变换的心电信号去噪研究［J］．仪器仪表学报，2013，34(5):1160-1166．

［10］李辉，郑海起，唐力伟．基于改进双树复小波变换的轴承多故障诊断［J］．振动、测试与诊断，2013，33(1):53-59．

［11］艾树峰．基于双树复小波变换的轴承故障诊断研究［J］．中国机械工程，2011，22(20):2446-2451．

［12］周西峰，朱文文，郭前岗．基于渐进半软阈值函数的超声信号去噪方法［J］．探测与控制学报，2011，33(2):35-39．