计算机专业离散数学教学研究

张剑妹，郭咏梅，赵秀梅

（长治学院 计算机系，山西 长治 046011）

1 引言

作为计算机专业的专业基础课[1-3]，离散数学是学生后续学习和工作的理论基础。对该课程的学习有利于提高学生的抽象思维、逻辑思维和计算思维能力，培养学生分析问题和解决问题的能力。但由于离散数学内容广、概念多、逻辑性与理论性强、高度抽象等特点，应用型本科院校计算机专业的学生将其列为最不感兴趣的课程之一。基于学生相对较弱的学习能力和追求实用的心理，教师必须突破原有的“定义-定理-证明”的教学模式，创造一种突出专业应用背景的更容易被学生接受的教学方法，以激发学生的学习兴趣，提高离散数学的教学效率。

2 课程定位与教学内容

长期以来，离散数学课程一直被作为一门纯数学课程讲解，始终未能摆脱“定义-定理-证明”的教学模式。课程定位和教学内容以定义的讲解和定理的证明为主，与专业应用背景相脱节，与应用型人才培养目标不相符。于是，应用型本科院校的教师开始思考学生应该学习离散数学的哪些内容，如何提高学生学习离散数学的兴趣，如何让离散数学成为提高学生的抽象思维和逻辑思维能力、培养学生用数学方法分析问题和解决问题能力的工具等一系列的问题。

按照《高等学校计算机科学与技术专业核心课程教学实施方案》[4]，应用型本科院校计算机专业的离散数学教学内容分为三个层次：核心知识单元、推荐知识单元和可选知识单元。核心知识单元包括数理逻辑、集合、关系、函数和图论初步；推荐知识单元包括证明技术和特殊的图；可选知识单元包括代数系统、基本计数和初等数论。在长治学院计算机专业的离散数学教学中，把核心知识单元作为主要内容进行详细讲解，对推荐知识单元中特殊图（包括欧拉图、哈密尔顿图、平面图和二部图）的定义和判定定理做详细讲解，对其典型应用作了引导性讲解。证明技术中的逻辑演算法是数理逻辑的重点内容，其他的证明方法融入到核心知识单元的集合、关系、图与树等相关章节中进行讲解。例如，在“集合代数”中应用多种方法证明集合恒等式及相关概念，在该章“典型例题”的讲解中又对所用证明方法进行了总结复习，以便学生熟练地掌握常用的证明技术。对推荐知识单元的内容进行了精心选择，基本计数中的包含容斥原理应用于集合中元素的计数已在“集合代数”中进行了详细讲解，代数系统的基本概念部分做了详细讲解，对半群、群、环、域、格等几种特殊代数系统的概念做了简要讲解，其他相关内容引导有余力的学生自学。

3 离散数学教学的改进思路与措施

3.1 利用简洁的语言，把复杂定义简单化

教学语言的简单化是指以简单易懂的语言把晦涩难懂的知识阐述明白。在离散数学中有很多用数学公式和数学语言给出的形式化定义，应用型本科院校的计算机专业学生理解这样的定义非常困难。为此，在离散数学教学中，我们通常将定义的内涵用简单的教学语言表达出来，以求达到通俗易懂的效果。例如，离散数学中关系闭包的定义是这样阐述的：“设R是非空集合A上的关系，R的自反闭包（对称闭包或传递闭包）是A上的关系R',且R'满足以下条件：①R'是自反的（对称的或传递的）；②R⊆R'；③对A上的任何包含R的自反关系（对称或传递关系）R''都有R'⊆R''。”在教学中我们通过三个条件内涵的简单阐述，引导学生得出这样一个概括性的定义，即“R的自反闭包（对称闭包或传递闭包）R'是A上的、包含R的、最小的自反关系（对称关系或传递关系）”。又比如，离散数学中对图同构的定义是：“设两个无向图G1=,G2=，如果存在双射函数θ:V1→V2，使得对于任意的e=(vi,vj)∈E1当且仅当e'=(θ(vi),θ(vj))∈E2，并且e与e'的重数相同，则称G1与G2是同构的，记作G1≌G2。”课堂教学中，我们用一个具体的图同构例子得出如下的图同构定义，即“如果两个图同构，这两个图实际上一个图的两种不同表现形式。”用这种简单通俗的语言概括出来的定义，也许不太准确，但却大大减轻了学生理解的难度，还可以借机教会学生使用公式描述概念的方法。

3.2 用计算机专业学生的思维教离散数学中的证明

应用型本科院校计算机专业学生的抽象思维能力较差，数学基础薄弱，这一点决定了他们不喜欢也不容易理解复杂的数学证明。在离散数学课中有大量的公式和定理需要证明，因此，如何用计算机专业学生习惯的、容易接受的方法教离散数学证明是一个颇具有挑战性的问题。文献[5]给出了几种利用计算机专业学生的知识背景教授数学证明的方法，笔者通过仔细研读、探索和补充，将其应用于离散数学的教学实践中，取得较好的教学效果。

（1）利用真值表进行数学证明是最容易被计算机专业学生所接受的。在离散数学教学中，我们将真值表应用于等值式的证明中。例如，量词否定等值式﹁∃xP(x)⇔∀x﹁P(x)的证明过程可用表1给出的真值表证明。

表1 ﹁∃xP(x)⇔∀x﹁P(x)真值表

（2）在计算机科学中，图是一个非常重要的工具，如果能将某些数学证明用图示的方法表示出来，一定能取得良好的教学效果。如，在集合恒等式中德.摩根律～(A∪B)=～A∩～B的证明可以用图1所示的文氏图表示出来，其中，图1a中阴影部分为(A∪B)，图1b中十字交叉部分为～A∩～B，通过这个文氏图，学生很容易理解该恒等式的真正内涵，也便于学生接受和记忆。

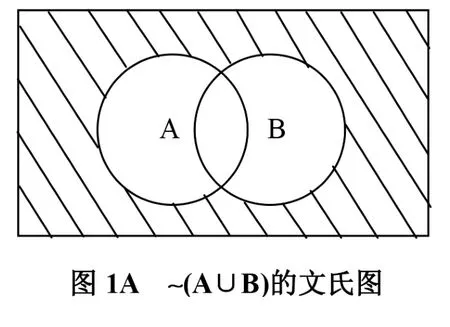
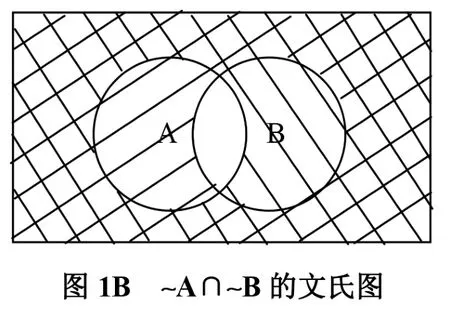
（3）计算机专业的学生非常熟悉算法这个概念，并且很多学生热衷于写算法和编程序，他们认为只要学会了写算法和程序就等于学会了计算机。鉴于学生的这种心理，笔者试图将算法用到了离散数学的证明中。如在证明主范式的存在性定理时，首先概括出求取主析取范式的算法步骤，然后再证明算法的正确性和完备性，最后，建议有余力的学生课后编程实现这个算法。通过这种方法，不仅解决了范式存在性定理的证明问题，同时也将离散数学和计算机科学结合起来，使学生认识到离散数学确实是计算机科学的基础，从而激发了学生的主动性。

3.3 使用计算机语言把离散数学和计算机科学联系起来

应用型本科院校计算机专业学生更注重专业技能的获得，他们对理论课的学习兴趣较弱。在他们心目中，只有计算机语言和程序才是计算机科学（这种观念在低年级学生中尤为普遍）。借鉴文献[6]的思想，离散数学课堂教学中，我们力求用计算机语言把离散数学和计算机科学联系起来。例如，在讲解关系运算和集合运算时，引入了关系数据库和SQL查询语言，针对学生管理数据库中的学生表S和课程表C设计了如下例子，要求学生用连接运算和集合运算完成，并鼓励学生在课外上机验证，以激发学生的学习兴趣。

例1．完成下列SQL查询。

①查询物理系和计算机系的所有学生的姓名；

②查询既选修C1和C3课程的学生的姓名；

③查询选修C1但不选修C3课程的学生的姓名；

④查询没有选修C2和C3课程的学生的姓名；这些查询实例有助于学生很好的理解逻辑运算和集合运算之间的关系。如①的两种SQL查询语句分别如下：

I.SELECT S.SNAME FROM S WHERE DEP=“物理系”and DEP=“计算机系”

II.SELECT S.SNAME FROM S WHERE DEP=“物理系”

UNION SELECT S.SNAME FROM S WHERE DEP=“计算机系”

例2.显示下列SQL语句的执行结果，分析该结果的正确性及其原因。

SELECT S.SNAME,C.CNAME FROM S,C

该例子的查询结果是表S和表C的笛卡尔积，无论学生与课程之间是否有选课关系，都会将学生名和课程名联接起来。

通过引入这些教学实例，不仅使学生理解了关系的定义和关系运算的内涵，而且让学生看到了离散数学在计算机科学中的应用，从而激发了学生的学习兴趣，调动学生学习的积极性。

3.4 引入实践教学环节，让学生理解离散数学在计算机科学中的应用

鉴于我校应用型人才培养目标，适当增加与计算机应用密切相关的实践学时，对学生较感兴趣或应用性较强的内容增课外开放性实验项目，以实验小组的形式延续课堂教学内容。在离散数学实践教学中作了如下尝试。

（1）通过布置课外开放性实验项目延伸课堂教学内容，揭示离散数学与计算机科学的关系，从而激发学生的学习积极性和主动性。

（2）通过网络课程教学平台延伸课堂教学内容。有限的课堂教学学时不足以让学生充分理解离散数学中较深较难的知识点，老师也不可能把离散数学的应用实例全部搬到课堂教学中。为此，课题组开发了离散数学学习网站，通过学习网站，学生不仅可以复习课堂教学的重点难点，进行在线测试，还可以通过知识拓展模块了解离散数学各知识点的应用，自行设计并完成相应的研究性实验项目，从而激发学生的学习兴趣。

4 结束语

几年的教学实践表明，以上教学方法对激发学生的学习兴趣、提高学生学习的积极性和主动性、增强教学效果是非常有效的。文中提到的教学实例仅是我们用于教学实践中的一部分，限于篇幅，不能一一列举。但是对离散数学教学方法的研究刚刚开始，还需要在教学实践中进行不断的研究和充实，以使其更好地服务于应用型本科院校计算机专业人才的培养。

［1］The Joint IEEE Computer Society/ACM Task Force on Computing Curricula Computing Curricula 2001 Computer Science［DB/OL］.http://WWW.acm.org/education/curric_vols/cc2001.pdf，2001.

［2］ACM/IEEE-CSJoint Task Force on Computing Curricula.2013.Computer Science Curricula2013［DB/OL］.ACM Press and IEEE Computer Society Press.DOI:http://dx.doi.org/10.1145/2534860.

［3］中国计算机科学与技术学科教程2002研究组.中国计算机科学与技术学科教程2002［M］.北京：清华大学出版社，2002.

［4］教育部高等学校计算机科学与技术教学指导委员会.高等学校计算机科学与技术专业核心课程教学实施方案［M］.北京:高等教育出版社，2009.

［5］Hongbiao Zeng,Keyu Jiang.Teaching Mathematical Proofs to CS Major Students in the Class of Discrete Mathematics［J］.Journal of Computing Sciencesin Colleges,2010,25(5):326-332.

［6］Anja Remshagen.Making Discrete Mathematics Relevant［C］.In:Proceedings of the 48th Annual Southeast Regional Conference,2010.