船—缆拖曳系统操纵性能分析

孙洪波，施朝健，林文锦

（1上海海事大学商船学院，上海200135；2集美大学航海学院，福建厦门361021；3中海油服，天津300450）

船—缆拖曳系统操纵性能分析

孙洪波1，2，施朝健1，林文锦3

（1上海海事大学商船学院，上海200135；2集美大学航海学院，福建厦门361021；3中海油服，天津300450）

为获取拖船在拖曳时的操纵性的变化规律。文章采用MMG船舶运动数学模型的建模思想，建立了六自由度拖船运动数学模型，采用有限差分法，建立了拖缆模型。然后，在此基础上建立将船-缆耦合起来以形成整个系统的运动数学模型,并分别采用龙格库塔方法对船舶运动积分求解，采用后向差分法对拖缆运动进行求解。通过对比仿真计算分析了水面拖船在拖带过程中的加速性能、旋回性能及偏转抑制性能。仿真结果表明在拖船与拖缆的相互影响下，拖船的加速性能和旋回性能有所下降而偏转抑制性能有所增强。

船舶运动数学模型；有限差分；加速性能；旋回性能；偏转抑制性能

0 引言

在各种海洋资源勘探及海底电缆铺设活动中，拖船拖曳是不可避免的环节。在海上，相比水下拖缆部分，水面拖船和拖缆上端靠近水面的部分受到风、波浪和海流的影响很大；而且水面拖船、拖缆之间存在着极为复杂的相互作用，构成了一个复杂的动态响应系统。对这个动态系统的动态特性进行研究，不仅可以更好地对拖缆进行控制，保证拖曳系统设备的可靠性和安全性，而且对保证拖船的安全操纵与航行具有理论上的指导作用和重要的工程应用价值。

国内外已有很多学者分别针对拖船和拖缆的运动建模与仿真预报进行了大量的理论研究。对于水面船体的研究，从上世纪50年代野本[1]建立了描述系统输入输出关系的响应模型、上世纪60年代以Abkowitz[2]为代表的整体建模理论的提出，以及上世纪70年代以小川阳弘等[3]为代表的MMG模型的提出，发展到现阶段，船舶运动模型虽然在某些方面的模型精度还有提高的空间，但已能满足工程及船员培训的需要，并得到广泛的应用。国内的贾欣乐、杨盐生[4]对船舶运动建模进行了详细而系统的总结与研究。水下拖缆自身运动的基础研究,早在上世纪60年代就已广泛地展开。拖缆水动力模型建模方法主要包括:集中质量法、有限元法、有限差分法和直接积分法等。例如：Walton和Polchaton[5]首先采用集中质量法研究了海军武器试验中水下锚链的二维运动响应，并给出详细的求解算法和公式。中岛俊夫等[6]建立了船舶系留锚链的三维集中质量法模型，并给出了详细的算例。Ablow等[7]在建立拖缆运动控制微分方程的基础上，采用有限差分法求解其的三维动态运动，与集中质量法相比空间与时间步长的选择具有更大的灵活性。有限元法和直接积分法更适用于拖缆静力分析，而不适合描述非定常状态下拖缆水动力性能[8]。国内的王飞、朱军等[9-10]在拖缆的建模与仿真方面，分别对集中质量法和有限差分法进行了详细的总结和研究；文献[11]采用了考虑拖缆弯矩和扭矩的有限差分法，可以对拖缆在低应力情况下进行计算。

通常，拖曳系统由水面拖曳母船、水下拖缆及一些缆载设备等组成，必需考虑船缆之间的相互影响才能准确预报其在各种情况下的运动响应特性。但现有的众多相关研究，考虑到拖缆相对于拖船质量比较小而忽略了船缆之间的相互作用，这必定会对整个系统的预报精度产生影响。文献[12]采用数值模拟手段，详细分析了拖缆对四自由度拖曳船舶操纵性能的影响；文献[13]采用集中质量法，对三自由度船舶与拖缆完全耦合的运动响应做了详细分析。本文在此基础上，首先采用MMG建模思想建立六自由度船舶运动模型，采用有限差分法建立拖缆模型，然后建立船缆相互作用，并考虑风浪影响的船缆拖带系统模型，最后，对该系统的动态响应进行仿真分析。

1 拖船和拖缆系统运动数学模型

研究船舶和拖缆在水中的运动时，一般采用两种坐标系统：惯性坐标系统和附体坐标系统，如图1所示。图中，o0x0y0z0为固定于地球表面的惯性坐标系统，规定x0指向正北，y0指向正东，z0垂直于地表指向上；ogxyz是原点位于船舶重心的附体坐标系。规定x指向船首，y指向右舷，z垂直于龙骨指向上；octnb是原点位于拖缆上的附体坐标系，规定t为拖缆切向，n和b为拖缆的两个法向；Θ、Φ、ψ为船舶在ogxyz坐标系下的欧拉角，θ、φ为拖缆在octnb坐标系下的欧拉角；vw、ψw、J和ψc分别为风速、风向、流速和流向。

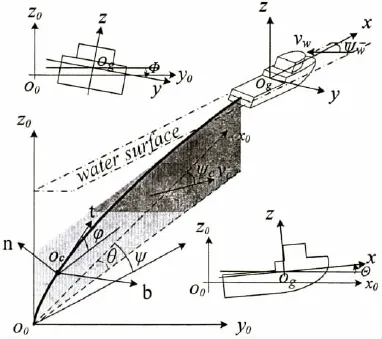
图1 拖船和拖缆坐标系统Fig.1 Ship and cable coordinates system

1.1 船舶运动数学模型

船舶的实际运动是一个具有6个自由度的复杂的运动。对于大多数情况下的船舶运动及控制而言，可以忽略船舶垂荡、横摇和纵摇运动，为了尽可能准确地反应船舶实际的运动姿态，本文采用考虑风、流、浪影响的六自由度船舶运动数学模型，其动力学方程如公式（1）。式中：X、Y、Z、K、M、N分别为作用于船体的力和力矩；m、mx、my、mz分别为船舶质量和各船舶附体坐标轴方向上的附加质量；I、Ia结合下角标分别为绕各船舶附体坐标轴的转动惯量和附加转动惯量。下角标H、P、R、cable、wind、current和wave分别表示船体、螺旋桨、舵、缆、风、流和波浪。公式（1）中各参数及力的详细计算可参考文献[4，14]。

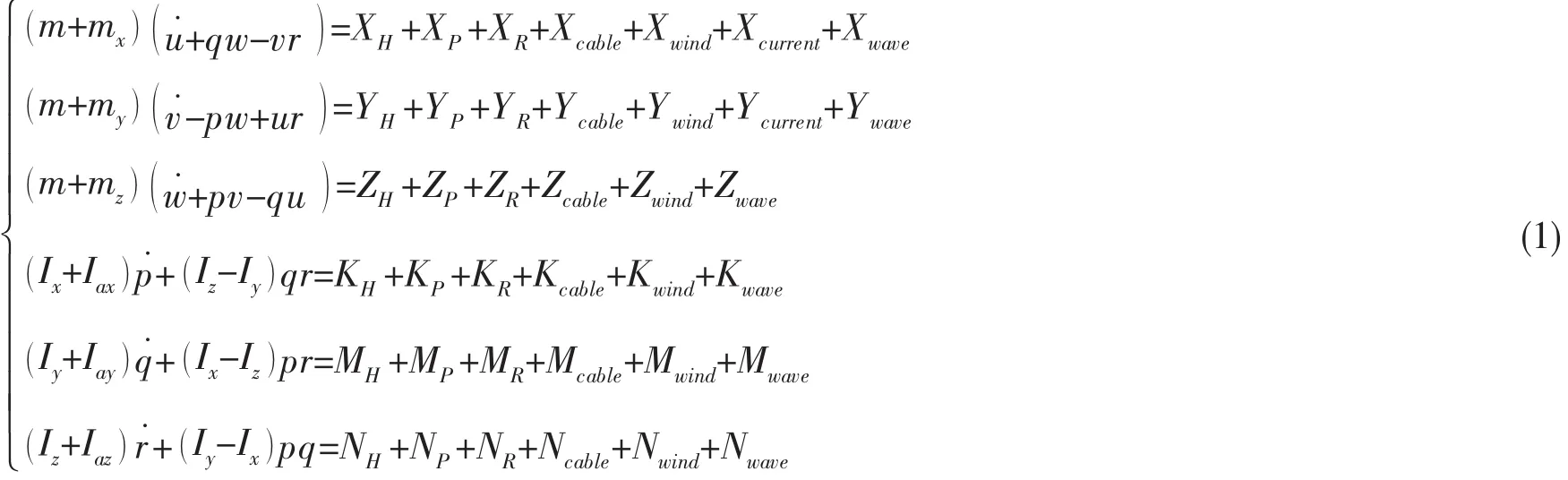
其中：u、v、w、p、q、r分别为船舶在ogxyz坐标系下的纵向、横向和垂向速度和绕各船舶附体坐标轴的角速度，与惯性坐标系内船舶运动学物理量之间的关系分别为公式（2）和（3）。

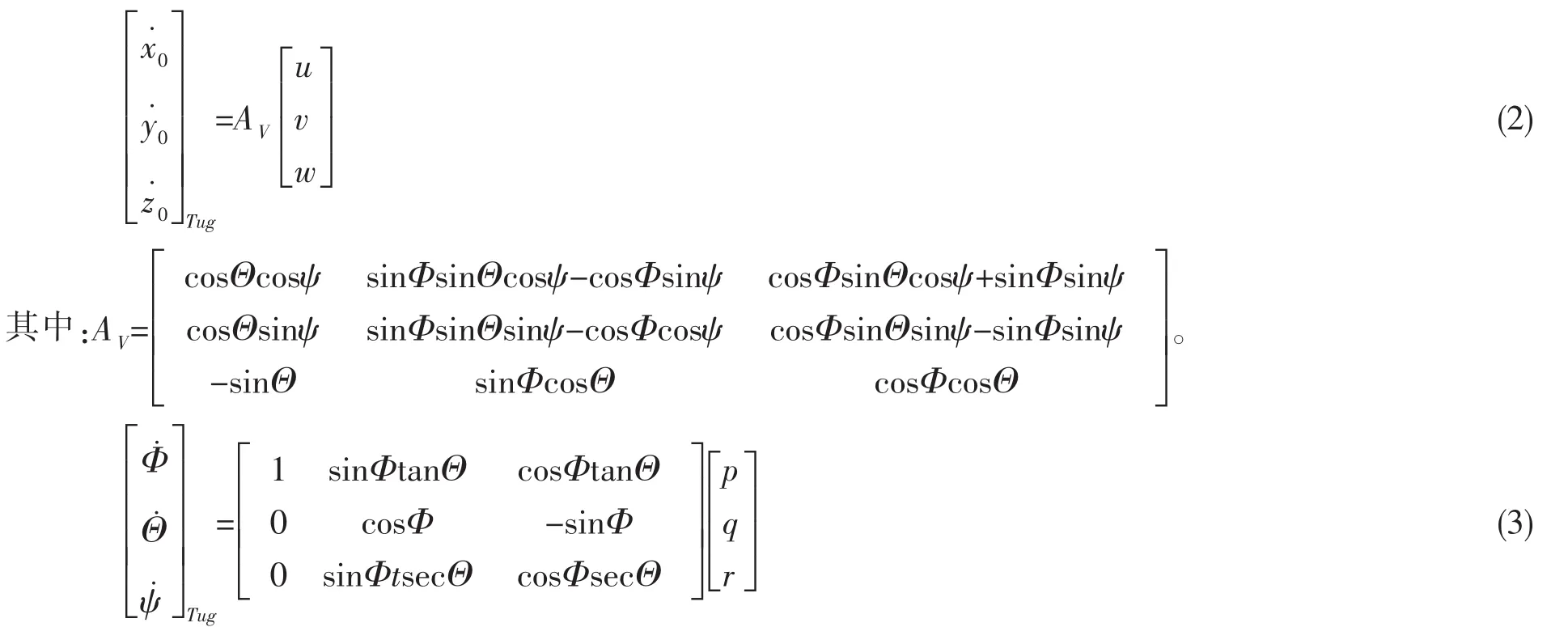
1.2 拖揽运动数学模型

设拖缆是细长、柔性和圆柱形状。拖缆上受重力、水动力和惯性力作用，由拖船拖动前进，不考虑拖缆所受的扭矩。拖缆微元Δs在t时刻所受张力、惯性力、水中重力和流体力分别为和以s表示未拉伸的拖缆长度，S是拉伸后的拖缆长度。考虑一般拖缆材料的拉伸特性有S′=坠S/坠s=1+eT，其中e=1/EA，E为拖缆弹性模量；A为拖缆横截面积。由于拖缆几乎全部位于水面以下，因此忽略了拖缆所受波浪力的影响。根据牛顿第二定律，拖缆微元的动力平衡方程如下：

同时联立方程（4）和（6），并将其在附体坐标系下展开，可分离得到6个独立的分量方程。这样，可以由6个变量T、Vt、Vn、Vb、θ和φ描述拖缆的三维运动。最终可以将拖缆系统的6个分量方程写成如下矩阵形式，其具体推导过程祥见文献[15]。

其中：ρ为海水密度；g为重力加速度；A为拖缆横截面积；m为每米拖缆质量；ρA为每米拖缆的附加质量；w=（m-ρA）g为水中每米缆质量；d=（1+eT）1/2d0为拉伸后缆的直径，d0为未拉伸缆的直径；Ct、Cn和Cb为拖缆的水动力系数；考虑均匀流的影响可知Ut=Vt+Jt，Un=Vn+Jn，Ub=Vb+Jb。

2 船—揽拖曳系统运动数学模型

为求解拖缆的三维动态运动，采用有限差分方法离散方程组（7）。设缆总长为s，把缆分成n段，节点数为n+1，然后将方程组按空间和时间两个方向上作向后差分，得到由6n个含有6n+6个未知变量方程组成的差分方程组。差分方程组只有6n个，故需补充拖曳系统端点边界条件使方程组得到封闭。

2.1 拖缆自由端边界条件

在拖缆自由端，即s=0处，拖缆张力与欧拉角的变化率均为零。因此，在自由端的边界条件可以直接表示为：

2.2 随船拖带点边界条件

拖带点处的边界条件由在惯性坐标系中，拖缆拖带端的三个速度分量VCx0、VCy0和VCz0与拖船上系固点的三个速度分量VTx0、VTy0和VTz0相等得到。前者具体形式可由公式（6）得到。而后者可根据拖船拖带点P（xP，yP，zP）距船舶重心的位置，通过解算船舶运动模型得到，其具体表达如下：

2.3 船—缆耦合条件

在拖曳系统运动过程中，拖船与拖缆是相互作用、相互影响的。拖船提供张力拖带着拖缆向前运动，反过来拖缆也影响了拖船的运动。因此，为进一步提高船缆拖曳系统在不同情况下的预报精度，必须将拖船和拖缆视为一个相互影响的整体进行考虑。船—缆耦合的主要方法有两种，一种是文献[16]采用的方法，即将拖船的运动方程离散成拖缆的方程形式，然后联立成方程组一并求解。该方法虽然能够保证船与缆之间的相互影响在时间步长上的同步性，但使整个系统的运动方程复杂化，并降低了解算效率。

本文的做法是将拖船与拖缆两个部分分别求解。拖船部分采用龙格库塔法，而拖缆部分采用有限差分法。这种处理方法思路清楚，物理意义明确，求解算法简单明了。虽然在解算过程中，是将拖缆前一时刻的张力作为作用在拖船上的影响力，但对于船缆拖曳这种低频运动系统，在较小的时间步长下仍能保证足够的精度。

具体的方法是根据（7）、（8）式和（9）式离散后的拖缆非线性运动方程组，在给定了拖点速度条件下采用Newton迭代法解算[15]，求得拖缆的形态及张力。在拖带点P（xP，yP，zP）已知的情况下，将求得的拖点张力经惯性坐标和船体坐标变换后，得到各船体坐标轴上的力和力矩，如下式：

将（10）式代入到（1）式中，用龙格库塔法解算（1）式的非线性微分方程组，从而得到拖船在拖缆影响下的操纵性能。缆索的动力学方程式（7）是一个一阶的非线性偏微分方程组。对其数值求解采用后向差分格式，如以i和j分别表示时间节点和空间节点，先在时域内对该方程利用后向差分格式进行离散，再在空间域内对方程仍采用中心差分格式离散。最后整理可得后向差分格式为：

对此非线性代数方程组（11），利用Newton-Raphson迭代法在时域内求解，即可求出任意时刻水中拖缆的运动姿态。

3 仿真计算

拖缆运动的计算涉及解算大型差分方程组，利用MATLAB软件结合并行算法对所建船—缆拖曳系统进行求解仿真。仿真所用拖船及拖缆的主尺度如表1和表2。

表1 拖船主尺度Tab.1 Towing ship main dimensions

表2 拖缆主尺度Tab.2 Towed cable main dimensions

为获取拖船在拖曳时的操纵性的变化规律，以及进一步提高水下拖曳系统在不同情况下的预报精度，分别对船—缆拖曳系统进行了加速、旋回和改向仿真试验。仿真结果如图2～4所示。

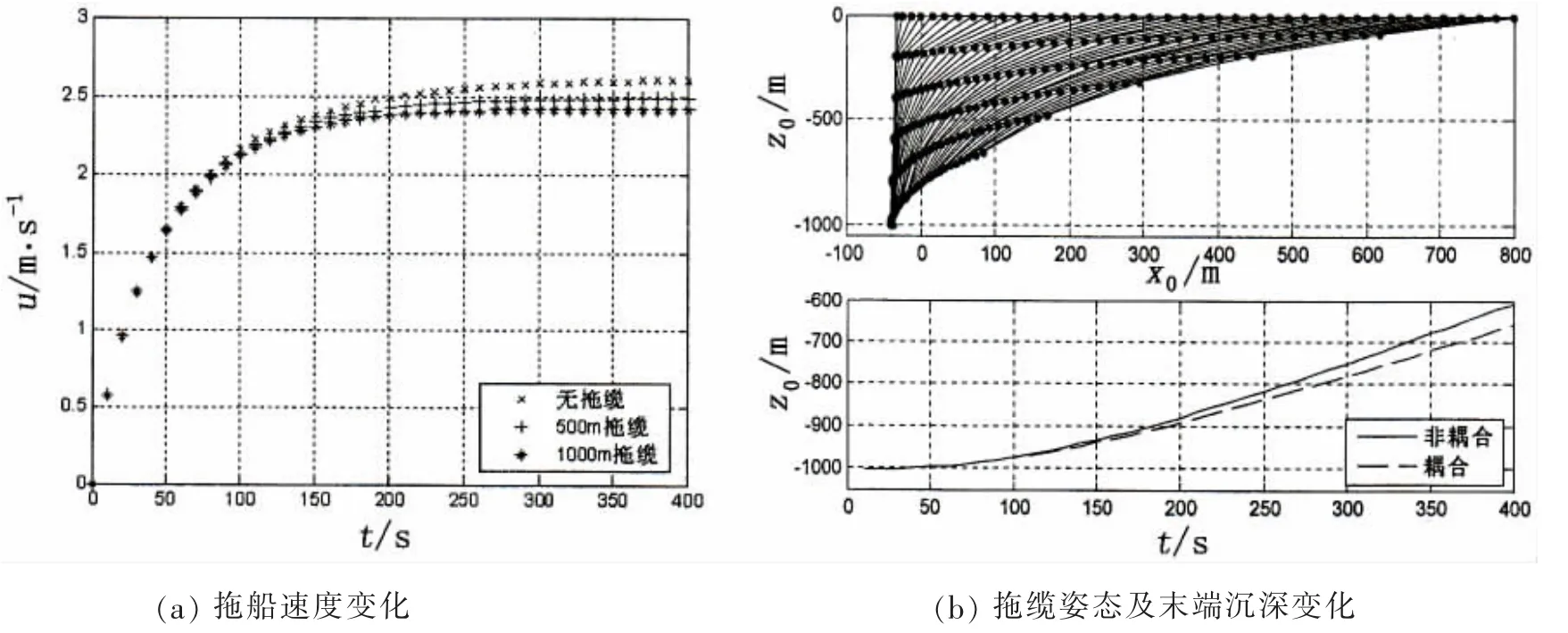
图2 系统加速过程仿真Fig.2 Acceleration simulation of towing system

变速性能是度量船舶惯性的技术指标，其包括加速、减速、停船和倒航性能，本文仅对拖曳系统的加速性能进行仿真。图2为系统仿真初始速度为零，螺旋桨RPM为50的仿真结果。从图2（a）中可以看出在拖缆的影响下，与无拖缆拖船相比，在相同的400 s加速过程中，随拖缆长度的增加，拖船的最终速度有所减小。图2（b）为1 000 m拖缆分为5段，6个节点的加速过程中的姿态变化。可以看出，随拖船速度的增加，各节点的浸水深度逐渐减小。图2（b）也给出了拖缆末端的沉深变化，同时可以看出船缆相互作用对拖缆末端沉深的影响随船速的增加差异越明显，加速末期，拖缆末端沉深相差近30 m。因此，为提高水下拖曳系统的预报精度，在加速阶段必须考虑船缆相互影响。

船舶的旋回性是船舶最基本的重要操纵性能之一，通常采用旋回初径DT与船长L之比DT/L，即相对旋回初径来衡量。图3为系统仿真初始速度为12 kns，螺旋桨RPM为124的仿真结果。从图3（a）中可以看出在拖缆的影响下，随拖缆长度的增加，拖船的旋回圈增大，且旋回舵角越小差异越明显，横距比进距变化明显。相对旋回初径如表3所示。

图3 系统旋回过程仿真Fig.3 Turning simulation of towing system

表3 拖带系统相对旋回初径Tab.3 Relative tactical diameter of towing system

图3（b）为500 m拖缆20°舵角旋回过程中的姿态变化。可以看出，由于拖船在旋回过程中存在明显的降速，因此，随拖带点速度的下降，各节点的浸水深度逐渐增加。图3（b）给出了拖缆末端的沉深变化，变化幅度近150 m，如直接认为旋回过程中速度不变，这显然是不符合实际情况的，将会引起不小的误差。同时可以看出船缆相互作用对拖缆末端沉深的影响，由于旋回过程中，拖船在有拖缆的情况下，由于船尾在拖缆的拉力及力矩的作用下降速明显。因此，旋回末期受拖缆影响减小，但相对于加速过程，拖缆末端的沉深有近5 m的差异。

为分析拖缆对拖船偏转抑制性即保向性的影响，本文采用10°/10°Z形仿真试验。系统仿真初始速度为12 kns，螺旋桨RPM为124，仿真结果如图4。从图4（a）中可以看出，无拖缆情况下的航向超越角与拖带500 m拖缆的情况差别不大，而与拖带1 000 m拖缆的情况差别明显。根据Z形仿真试验结果，可以方便地计算出上述三种仿真试验工况下拖船的旋回性指数K和追随性指数T，具体计算方法见文献[17]。计算结果如表4所示，其中：K′=KL/Vs；T′=KVs/L为K和T的无量纲化，L为船长，Vs为船速。计算结果表明拖船在拖缆的影响下，旋回性指数K减小说明拖船的旋回性能变差，且拖缆越长旋回性越差。这一点同旋回仿真试验的结果是一致的；追随性指数T减小说明船舶应舵快，易于保向。总体来说，拖船的旋回性变差，追随性变好，但操舵后，虽然应舵较快，但定常旋回角速度小，旋回圈大。

从图4（b）中可以看出，由于拖船在改向时存在降速而引起的拖缆末端沉深的变化。同时可以看出船缆相互作用对拖缆末端沉深的影响比较明显，Z形仿真试验末期，拖缆末端沉深相差近2.5 m。

图4 系统改向过程仿真Fig.4 Altering course simulation of towing system

表4 拖带系统操纵性指数Tab.4 Maneuverability indices of towing system

4 结论

本文为获取拖船在拖曳时的操纵性的变化规律，以及进一步提高水下拖曳系统在不同情况下的预报精度，将水面拖船和水下拖缆视为一个相互影响的整体进行考虑。其中，水面拖船的运动采用六自由度的MMG模型，而水下拖缆则采用有限差分法进行建模，在此基础上建立了考虑拖船与拖缆的相互影响船-缆拖曳系统运动数学模型，并采用四阶龙格库塔方法和后向差分法对拖船与拖缆两个部分分别求解。最后，分析了包括水面拖船在内的整个系统的操纵运动响应。仿真试验结果表明，受拖缆影响，拖船加速性能下降，拖缆长度越长速度下降越明显；拖船的旋回直径增大，旋回性能随缆长的增加而下降，且旋回舵角越小差异越明显；拖船的偏转抑制性有所增强。此外，由于拖船在旋回和改向过程中存在降速的影响，拖缆的姿态变化更为符合实际的运动特征。

[1]野本謙作,田口賢士,本田啓之輔,平野進.船の操性に就いて(1)[J].日本造船協会论文集,1956,99:75-82. Nomoto Kensaku,Taguchi Kenshi,Honda Keinosuke,Hirano Susumu.On the steering qualities of ships(1)[J].The Japan Society of Naval Architects and Ocean Engineers,1956,99:75-82.

[2]Abkowitz M A.Lectures on ship hydrodynamics steering and manoeuvability[R].Hydro-and Aerodynamics Laboratory Report No.Hy-5,Lyngby,Denmark.1964.

[3]小川陽弘,小山健夫,貴島勝郎.MMG报告-I操縱運動の数學モデルにつぃて[J].日本造船學會志,1977,575:192-198. Ogawa Youko,Koyama Keno,Takashima Katsuro.MMG Rep-1 mathematical model for motions of ships[J].Journal of The Society of Naval Architects of Japan,1977,575:192-198.

[4]贾欣乐,杨盐生.船舶运动数学模型—机理建模与辨识建模[M].大连:大连海事大学出版社,1999:234-246. Jia Xinle,Yang Yansheng.Ship motion mathematical model[M].Dalian:Press of Dalian Marine University,1999:234-246.

[5]Walton T S,Polachech H.Calculation of transient motion of submerged cables[J].Mathematics of Computation,1960,14: 27-46.

[7]Ablow C M,Schechter S.Numerical simulation of undersea cable dynamics[J].Ocean Engineering,1983,10(6):443-457.

[8]苑志江,金良安,田恒斗,卢祎斌.海洋拖曳系统的水动力理论与控制技术研究综述[J].科学技术与工程,2013,13 (2):408-420. Yuan Zhijiang,Jin Liang’an,Tian Hengdou,Lu Yibin.Comments on the research of hydrodynamic and controltechnology of underwater towed system[J].Science Technology and Engineering,2013,13(2):408-420.

[9]王飞.海洋勘探拖曳系统运动仿真与控制技术研究[D].上海:上海交通大学,2007. Wang Fei.Simulation and control research of marine towed seismic system[D].Shanghai:Shanghai Jiao Tong University, 2007.

[10]朱军,熊鹰,王志国.拖缆系统直线定常运动仿真计算[J].海军工程大学学报,2001,13(2):17-20. Zhu Jun,Xiong Ying,Wang Zhiguo.Towed cable behaviour during straight moving[J].Journal of Naval University of Engineering,2001,13(2):17-20.

[11]Liu Tao,Zhang Weijing,Ma Jie,Zhang Guanglei.Transient dynamic analysis of towed low-tension cable with experimental verification[J].Journal of Ship Mechanics,2013,17(3):197-213.

[12]朱军,黄若波,胡忠平.拖曳系统对舰船操纵性影响计算[J].船海工程,2002,145(2):5-10. Zhu Jun,Huang Ruobo,Hu Zhongping.Calculation of towing system effects on ship maneuvering[J].Ship&Ocean Engineering,2002,145(2):5-10.

[13]王飞,黄国樑,伍生春.水下拖曳系统缆-船耦合运动模拟[J].上海:上海交通大学学报,2011,45(4):571-575. Wang Fei,Huang Guoliang,Wu Shengchun.Dynamic research on the coupling response of cable-towing ship system[J]. Journal of Shanghai Jiao Tong University,2011,45(4):571-575.

[14]李积德.船舶耐波性[M].哈尔滨:哈尔滨船舶工程学院出版社,1991. Li Jide.Seakeeping[M].Harbin:Press of Harbin Engineering University,1991.

[15]邓德衡,黄国樑,楼连根.拖曳线列阵阵形与姿态数值计算[J].海洋工程,1999,17(1):18-26. Deng Deheng,Huang Guoliang,Lou Liangen.Numerical calculation of towed array shape and attitude[J].Ocean Engineering,1999,17(1):18-26.

[16]李英辉,连琏.拖曳声纳系统仿真运算研究[C].第十二届中国海岸工程学术讨论会论文集,2005. Li Yinghui,Lian Lian.The towed sonar system simulation computing research[C].The 12th Academic Conference on China Coastal Engineering,2005.

[17]古文贤.船舶操纵[M].大连:大连海事大学出版社,1993:53-55. Gu wenxian.Ship Handling[M].Dalian:Press of Dalian Marine University,1993:53-55.

Analysis of maneuverability of towing cable ship system

SUN Hong-bo1,2,SHI Chao-jian1,LIN Wen-jin3
(1.Merchant Marine College,Shanghai Maritime University,Shanghai 200135,China;2.Navigation College, Jimei University,Xiamen 361021,China;3.COSL,Tianjin 300450,China)

For obtaining the regular rules of a cable towing vessel,the following methods are adopted.According to the MMG ship motion mathematical modeling theory,a 6dof ship motion mathematical model was built.And a 6dof cable motion mathematical model was established with finite difference method.Then,a coupling ship-cable system model was established.Finally,the system motion simulations containing acceleration,turning and zigzag maneuvering were carried out,and the results indicate that the abilities of acceleration and turning are decline,but yaw checking ability is enhanced.

ship motion mathematical model;finite difference method;acceleration ability; turning ability;yaw checking ability

U661.33

A

10.3969/j.issn.1007-7294.2015.11.005

1007-7294（2015）11-1325-09

2015-06-13

国家自然科学基金资助项目（51109090）；李尚大集美大学学科建设基金资助项目（ZC2010011）

孙洪波（1977-），男，讲师，博士研究生，E-mail：sunhongbo1977@126.com；

施朝建（1951-），男，教授，博士生导师。