基于MIMO法的行星齿轮减速器的模态试验
2015-04-26张坤于洋余晓辉
张坤,于洋,余晓辉
(中国船舶重工集团公司第七〇三研究所,哈尔滨150078;2海军驻哈尔滨七〇三所军事代表室,哈尔滨150078)
基于MIMO法的行星齿轮减速器的模态试验
张坤1,于洋2,余晓辉1
(中国船舶重工集团公司第七〇三研究所,哈尔滨150078;2海军驻哈尔滨七〇三所军事代表室,哈尔滨150078)
针对行星齿轮减速器,采用MIMO方法进行模态试验,将方案一(弹性绳悬挂)和方案二(弹性绳和充气轮胎混合支撑)两种形式下高频信号和低频信号得到的六组试验数据用LMS模态分析软件进行处理,得到七阶模态频率及其振型,及各阶模态的模态质量、模态刚度和模态阻尼等信息。最后分别对两种方案进行模态可信度和有效性分析,分析结果表明,两种方案在模态参数估计上都能取得相对合理的结果,方案二在获取低频模态信息方面效果较好,而方案一在获取高频模态信息方面效果较好,具体应用时应根据所关心的频段和模态参数选取不同方案的数据进行参考。
行星齿轮减速器;模态试验;LMS;最小二乘复指数法
0 引言
模态参数对于机械系统的故障诊断、结构修改及优化设计、振动噪声控制等领域有着广泛的应用。目前,模态分析技术已日趋成熟和完善,各种试验方法和处理手段越来越多,这对保证各种机械产品和工程结构的高性能指标、高使用安全性和高可靠性起着重要作用[1]。常用的试验模态分析方法有SIMO、MISO和MIMO,其中SIMO为单输入多输出,即单点激励多点响应,MISO为多输入单输出,即多点激励单点响应,MIMO为多输入多输出,即多点激励多点响应[2]。MIMO时域模态分析是测试模态参数比较理想的手段,与频域模态分析相比,它有计算精度高,且不易丢失模态的优点[3]。为保证能激励出行星减速器2 000 Hz内的所有固有频率,试验决定采用多输入多输出的模态参数识别方法,即MIMO方法。对于试验模态分析,影响因素较多,边界条件的设定,激励点数量与布置位置的选择,响应点数量与分布位置的选择,激振力大小的确定等,都会给试验模态带来一定的难度。本次行星减速器模态试验采用MIMO方法,在两种支承形式下共采集到了六组试验数据,经后续分析得到的模态参数可为行星减速器的应用提供指导,并可为今后的结构动力学改进设计提供参考依据。
1 模态试验原理
基本原理是人为给机械加激振力,同时测出其响应。接着将信号经数据采集系统进行采样,然后输入到计算机,用分析软件将数据经快速FFT变换,算出激振点与响应点的传递函数[4]。
模态分析计算如图1所示。

图1 模态分析计算原理图Fig.1 Principle diagram of modal analysis
2 模态试验内容
2.1 悬挂条件
使被测设备处于何种状态是试验准备工作的一个重要方面,较为常用的一种试验状态是自由状态,即使试验对象自由悬浮在空中。这种状态下有六个刚体模态:三个平移模态和三个转动模态。如有可能,应该使悬挂点尽可能靠近模态变形最小的节点。
为了使各组试验所测的数据尽可能客观地反映自由状态下行星减速器的模态及振型,根据试验件的结构特点,本试验共设计两套方案:
方案一:
采用弹性绳悬挂减速器,同时用尼龙绳对减速器进行保护。本方案没有限制基座的侧向位移,减速器处于完全自由状态。试验装置如图2,图3所示。
方案二:
弹性绳和弹性橡胶垫(即充气轮胎)的混合支承方案。把减速器放置在充气轮胎上,可充分利用其弹性大并能较好控制重心偏移的优势,同时采用弹性绳悬挂承载部分拉力,可帮助控制试验过程中可能出现的减速器重心偏移、侧向位移过大等问题。

图2 悬挂及保护装置实物Fig.2 Material object of suspension and protective device

图3 方案一装置效果图Fig.3 Device effect picture of scheme 1
2.2 试验设备
行星减速器频响函数测量基本框图如图4所示。

图4 频响函数测量基本框图Fig.4 Measure elemental box of frequency response function
由于本试验的频带相对较宽,试验共分低频和高频两组带宽进行。低频组测试时带宽设置为0~512 Hz,分辨率为0.25 Hz;高频组带宽设置为2 048~2 560 Hz,分辨率为0.312 5~0.5 Hz。由于试验过程中主要干扰信号为高频信号,而高频组测试的结果同样包含低频信号成分,模态分析时可将低频信号进行分离。本次试验低频组针对两种支承方式各进行一组测试,高频组针对两种支承方式共进行四组测试。试验在两个激励点各采用随机激励和猝发随机激励方式,原理如前所述。选择保存频响函数中的动态刚度和相关函数,经系统调试选取好量程后便可开始测量。
2.3 激振点位置选取和激励方式选取
对于质量大的研究对象,单点激励不能将完整的结构模态特性激励出来,而多点激励才能将结构的模态特性激励出来[5]。为保证能激励出2 000 Hz内的所有模态参数,试验决定采用多输入多输出的模态参数识别方法MIMO法。激振器的激振点的选择应遵循以下两点:(1)选在刚度较大且便于激励的地方;(2)应避开结构模态节点或者支撑点,因此不宜选在对称的平面上[6]。同时试验应当保证激振器能提供足够的能量使各测试点所测得的信号有足够大的信噪比,但又不至于由于激励力过大而引起局部信号失真;同时还要考虑到激振器的安装和固定等问题。试验针对上述要求进行了大量测试,最终的激励位置示意如图5,图6所示。选择位于不同侧的两个位置进行激励,可以保证能提供足够的能量激励出所有的模态,使各测点所测的信号具有较好的信噪比,又能避免由于激励位置距离太近而引起靠近激振点位置处振动信号过大,而远离激振点位置振动信号微弱的问题。同时对试件进行两个方向的激励,尽可能避免出现模态丢失现象。本试验对象质量较大,激振器附加质量的影响可忽略不计。

图5 激振器位置简图Fig.5 Position sketch of vibration exciter

图6 激振器位置模型示意图Fig.6 Scheme of vibration exciter position model
2.4 模态试验
方案一和方案二所采集得到的信号数据如表1和表2所示的结果。

表1 由方案一所得模态参数Tab.1 Mode parameter of scheme 1

表2 由方案二所得模态参数Tab.2 Mode parameter of scheme 2
将计算得到的所有模态数据采用最小二乘法进行拟合,最终可得到表3-5的模态参数。

表3 行星齿轮减速器整体频率Tab.3 Frequency of planetary gear reducer

表4 行星齿轮减速器整体阻尼Tab.4 Damp of planetary gear reducer

表5 行星齿轮减速器模态参数Tab.5 Mode parameter of planetary gear reducer
3 两种方案模态可信度和有效性分析对比
3.1 方案一模态可信度分析
由模态分析理论可知,系统各模态间应相互正交,即任意两组模态的相关系数为0。但由于试验过程不可能在理论的假设条件下进行,所采集的信号将不可避免地偏离真实信号,这将直接导致试验所得的结果与理论出现偏差。经过分析计算,方案一的自相关函数数据如表6所示。柱状图中对角线值为各阶模态的自相关系数,由于是其自身的比较,故都为100%;柱状图各非对角线上的元素为各阶模态之间的相关函数值,可以看出,低阶模态间相似程度相对较高,高阶模态间相似度较差,几乎可以忽略,低阶模态与高阶模态间的相似度也很低。总体来说,方案一所得到的各阶模态基本符合模态正交理论。

表6 由方案一所得模态自相关函数表Tab.6 Mode autocorrelation function table of scheme 1
3.2 方案一模态有效性分析
在某一测点给结构附加一质量,会降低所有模态的有阻尼固有频率。这一理论特性构成评价模态振型向量的一个判据。对于每一测点而言,各固有频率对该测点质量增加的灵敏度是可以求出的,且应该是负值。对应某一阶模态(k)的“模态超复性”MOV定义为在该测点附加质量后,固有频率确实降低的这种测点所占的加权百分比,即:

其中:wi为加权因子,取wi=1(不加权)或,若是对于第k阶模态而言,在测点i附近附加质量后的固有频率灵敏度为负值;aik=0其他情况[7]。
经过对方案一中一组低频信号和三组高频信号进行分析,并对比各组数据后对模态参数进行了修正,最终得到如表7所示的函数值。

表7 由方案一所得相关函数值Tab.7 Correlation function value of scheme 1
表7中,MOV代表模态超复性,MPC代表模态相位共线性,MPD代表平均相位偏移,MP代表模态参预。
由前述MPC和MPD函数意义可知,方案一所得模态低阶部分MPC都具有较高值,前两阶模态MPC值甚至接近100%;同时MPD值也较低,即同一模态各个复数的模态振型系数之间共线性较好,近似同相。这表明低阶部分模态清晰,模态置信度很高,且都为实正则模态。而高阶部分MPC值明显较低阶部分小,均在80%左右,且MPD值表明各模态振型间共线性相对较差。这主要是因为试验环境相对较差,高阶信号干扰较多,同时高阶部分局部模态较为密集,不利于对整体模态进行筛选。
总体讲,方案一所得数据在低频段具有较好的可信度,同时对多组数据分析发现方案一所得模态参数在低频段具有很高的可重复性。而对于高阶频段部分,由于试验中不可避免存在各种干扰和误差,导致方案一高频段模态数据可信度较低频段差,不适用于系统的整体模态分析,此处列出主要用于和方案二作对比分析用。
方案二模态自相关函数数据列表如表8所示。

表8 由方案二所得模态自相关函数表Tab.8 Mode autocorrelation function table of scheme 2
3.3 方案二模态可信度分析
由MAC函数可以看出,由方案二所得的自相关函数值低频部分相对较高,其中所得的第二阶模态和第三阶模态相似度最高,高达76%。可知第二组试验进行过程中受到了较强的低频信号干扰,同时也可能是由于支承方式的改变引起了模态参数的变化和信号的失真。除此之外,其他模态间相似度较低,高阶模态之间相似度均在5%之内,说明此时高频段内受到的干扰信号较小,模态选取时参数设置得当。另外高阶模态与低阶模态间相似度都在10%以内,即本方案整体讲能很好地排除高频段信号干扰,但由于支承方式的改变同时放大了低频段的干扰信号。
3.4 方案二模态有效性分析
经过对方案二中一组低频信号和一组高频信号进行分析,对比两组数据后所得到的相关数据对模态参数进行了修正,最终得到如表9所示的MOV值。
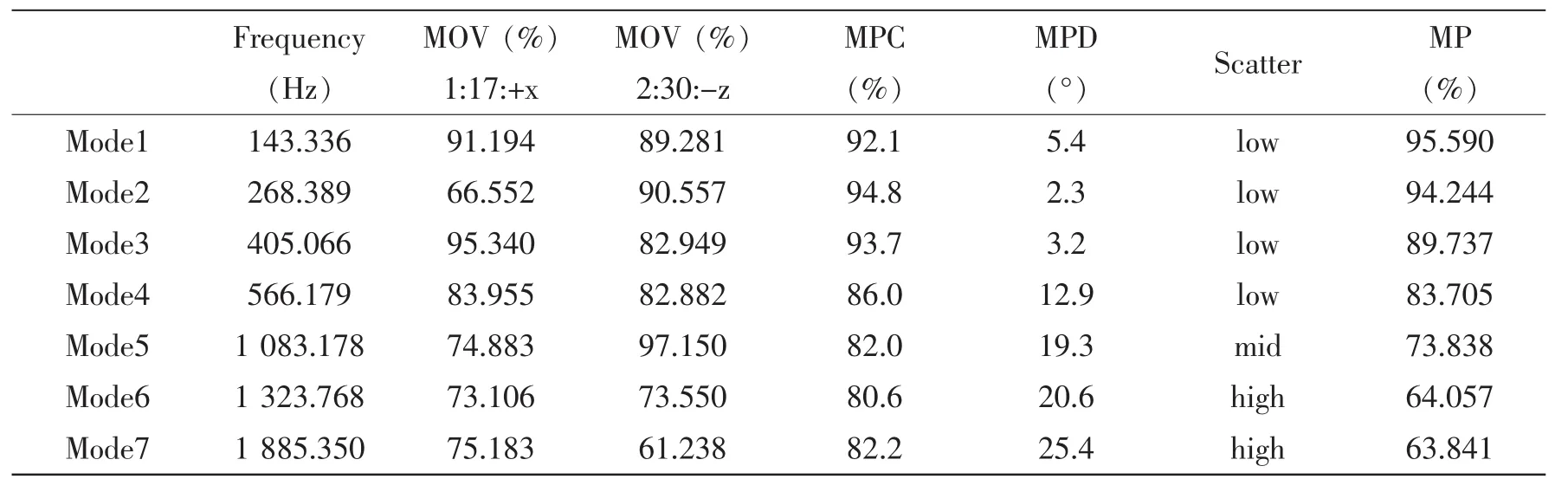
表9 由方案二所得相关函数值Tab.9 Correlation function value of scheme 2
由表9可以看出,方案二所得到的模态相位共线性MPC和平均相位偏离MPD平均值相对稳定。低频部分四阶模态MPC值均在90%左右,且平均相位差较小,即低频部分模态共线性较好。相对低频部分,高频段所提取的三阶模态整体效果略差,模态相位共线性MPC值均在80%附近,且平均相位偏离较大,表明模态共线性相对较差。表明方案二虽然在处理噪声干扰方面有较大优势,但由于近似处于完全自由状态,在减小高频段信号干扰的同时低频段信号的干扰得到了放大。
整体上看,两种方案在模态参数估计上都能取得相对合理的结果,但方案一整体效果比方案二好。两种方案在提取系统模态频率和振型方面差别不大,但在阻尼的方面方案二比方案一所得数据更接近真实值。在模态刚度,模态质量和模态阻尼方面,两种方案所得结果在数量级上差别不大,都能满足要求。方案二在获取低频模态信息方面效果较好,而方案一在获取高频模态信息方面效果较好。具体应用时应根据所关心的频段和模态参数选取不同方案的数据进行参考。
4 结论
本次行星减速器模态试验采用MIMO方法,在两种支承形式下共采集到了六组试验数据,运用LMS模态分析软件对所得数据进行分析,共得到七阶模态参数。经分析,所得各阶模态数据均具有较高的置信度,可为行星减速器的应用提供指导。
[1]Yao C C,Chang K C,Lee C C.Damage diagnosis of steel frames using vibrational signature analysis[J].Engineering Mechanics(ASCF),1992,118(9):1949-1960.
[2]张新玉,张文平,李全,王芝秋.圆柱形薄壳结构的试验模态分析方法研究[J].哈尔滨工程大学学报,2006,27(1): 20-25. ZhangXinyu,ZhangWenping,Li Quan,Wang Zhiqiu.Experimental modal analysis method of cylindrical thin shell structures[J].Journal of Harbin Engineering University,2006,27(1):20-25.
[3]陈朝阳,石琴,钱锋,温千虹,张翔.驱动桥壳多输入/多输出时域模态分析[J].合肥工业大学学报,2000,23(4): 468-472. Chen Chaoyang,Shi Qin,Qian Feng,Wen Qianhong,Zhang Xiang.MINO experimental modal analysis in time domain for drive axle housing[J].Journal of Hefei University of Technology,2000,23(4):468-472.
[4]范秀杰,赵宇.某发动机低压涡轮轴模态试验研究[J].科技创新导报,2014,32:36. Fan Xiujie,Zhao Yu.Experimental modal analysis for low pressure turbine shaft of engine[J].Science and Innovation Herald,2014,32:36.
[5]焦安超,冯咬齐.‘天宫一号’目标飞行器结构模态试验方法[J].航天器环境工程,2011,28(6):593-596. Jiao Anchao,Feng Yaoqi.Method of structural modal test for Tiangong-1 target spacecraft[J].Spacecraft Environment Engineering,2011,28(6):593-596.
[6]张华鑫,童敏勇.某轿车白车身模态试验分析研究[J].机械研究与应用,2014,27(3):107-109. Zhang Hanxin,Tong Minyong,Modal test analysis and research for body-in-white[J].Mechanical Research and Application,2014,27(3):107-109.
[7]傅志方,华宏星.模态分析理论与应用[M].上海:上海交通大学出版社,2000. Fu Zhifang,Hua Hongxing.Modal analysis theory and application[M].Shanghai:Press of Shanghai Jiaotong University, 2000.
Modal test of planetary gear reducer based on MIMO method
ZHANG Kun1,YU Yang2,YU Xiao-hui1
(1.The 703 Research Institute of CSIC,Harbin 150078,China;2.Military Delegate Office in Harbin 703 Research Institute,Harbin 150078,China)
Multiple Input Multiple Output(MIMO)method was applied to experimental modal analysis methods on planetary gear reducer for modal test and analysis.Six groups test data under high frequency signal and low frequency signal in scheme 1(suspension of elastic rope)and scheme 2(mixed supports of inflation tire)two support forms were processed by using LMS test.Lab 10a test software.System seven-order mode frequency and shapes,mode mass,mode stiffness,mode damp,and so on were obtained.Finally, mode reliability and validity were analyzed between scheme 1 and scheme 2.Analysis results show that both scheme 1 and scheme 2 have relatively logical results,scheme 2 has better effect in obtaining low frequency mode information and scheme 1 has better effect in obtaining high frequency mode information.Frequency range and mode parameter should be taken over when applying.
planetary gear reducer;modal test;LMS;the Least Square Complex Exponent method
TH132.4
A
10.3969/j.issn.1007-7294.2015.11.011
1007-7294(2015)11-1377-08
2015-09-24
张坤(1985-),女,工程师,E-mail:zhangkun19851027@163.com;
于洋(1982-),男,工程师。
