一种斜导面码垛机器人结构静力学分析研究

郑秀宏，李锻能，姚松亮

(广东工业大学机电工程学院，广东广州510006)

0 前言

目前，工业机器人正呈现出爆发式增长态势，世界各地纷纷掀起使用工业机器人热潮。我国工业机器人研究和应用始于20 世纪70年代，受当时经济体制等因素的制约，发展比较缓慢，导致研究和应用水平均比较低。而国外工业码垛机器人以其在适用范围、工作性能、功耗、负载等方面的优势大量应用于国内各类生产线上，并逐步占领市场，但价格居高不下［1－2］。

本作者在综合分析国内外并联与串联机器人结构特点的基础上，对比多种结构的各自优点，研制出一种新型串并混联斜导面码垛机器人，具备工作范围大、承载能力强等特点。在完成整机功能结构设计后，进行整机结构静力学分析研究，试图改进整机结构，使其静力学性能得到进一步提升，为工业应用提供参考。

1 斜导面机器人结构简介

该码垛机器人的独特之处是其大臂沿与水平呈斜角的导向面直线移动，构成机器人的关节运动。机器人主要由底座、腰部、末端执行器、小臂、大臂、小臂驱动臂、斜面滑块以及平行保持架这8 个部分组成 (见图1)，能实现底座旋转、大臂前后运动、前臂上下运动和末端执行器的回转运动。

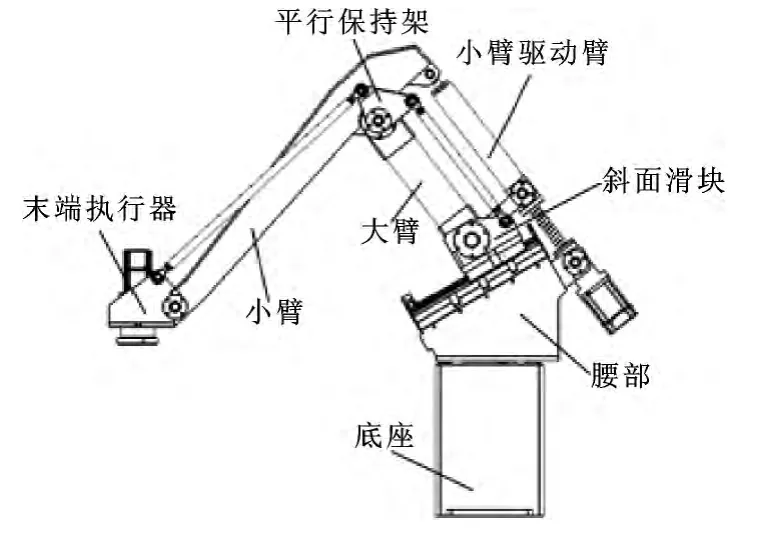
图1 码垛机器人结构简图

机器人的运动关节采用减速机+ 电机组合或者丝杆+ 电机组合进行驱动，构成4 轴驱动。小臂驱动臂结构通过采用关节球轴承与丝杆、丝杆套筒联合装置，使其受力始终沿轴向，提升了力的传递效率。一直处于拉伸态的小臂驱动臂丝杆在工作过程中承受了较大的轴向力，符合细长杆件的受力结构。

该结构机器人斜导向面的倾斜角θ 是影响大臂受力以及整机承载变形的重要参数 (见图2)。假设L1为水平导轨，L2为改进后的斜面导轨，可见到在空间差异不大的情况下，L2＞L1，即倾斜的导轨有利于增大滑块的移动范围，扩大机器人的运动空间。同时大臂作用在水平导轨L1上的力F1分解为F1x和F1y，F1y由导轨承担，F1x则对丝杆产生不利的轴向力，严重影响丝杆、丝杆轴承及轴承座的寿命。改进后，导轨与水平面夹角变为θ，则大臂作用在斜面导轨L2上的力F2在x2方向分量趋于0，此时丝杆受到的轴向力大大减小，一定程度上延长丝杆及其附件寿命，并保证丝杆的传动精度。

图2 导轨面改进前后受力简图

2 典型位姿系列斜面倾角机器人静力学分析

机器人静力分析是计算在固定不变载荷作用下重要部件的位移、应力，最终达到提高其整机末端静刚度、位置精度的目的，因此静力分析为机器人的结构改进提供重要参考［3］。进行静力学分析前，将已用SolidWorks 建好的三维模型进行简化 (去螺纹孔及其他一些不重要的特征)，这些简化对分析结果的影响可忽略不计［4］。

该构型机器人在水平位姿 (反向悬臂位姿)和竖直位姿 (最大高度位姿)两种状态稳定性较差，而处于最小包络体积位姿 (收拢状态)时稳定性好［5］。故而选择机器人不同斜导面倾角情况下的竖直、水平两种典型姿态，进行整机静力学分析。

通过SolidWorks 的有限元模块SolidWorks Simulation 对不同斜导面倾角的整机进行静力学分析，得到整机在最大载荷情况下工作空间内应力、位移场的分布特性。

材料设置:底座、腰部、大臂、平行保持架的材料为普通碳钢，小臂驱动臂 (含丝杆)、斜面滑块(含丝杆)的材料为合金钢，小臂、末端执行器的材料为2024 合金，材料的详细信息如表1 所示。

表1 材料明细表

边界条件与载荷约束:斜面码垛机器人各构件由轴和轴承或丝杆连接，可将各构件间的连接方式设置为销钉连接或滑移面连接，并添加接触面摩擦因系数为0.05。将底座安装板设置为固定几何体约束，添加引力，同时在末端执行器上施加1 000 N的载荷。

网格划分:实体网格的划分采用标准网格器，单元大小为设置20 mm，公差为1 mm，雅可比点设置为4 点。

2.1 水平位姿情况下不同倾角的有限元分析

分别选取θ =15°、20°、25°、30°、35°、40°作为系列斜面倾角进行整机的执行件最远端 (水平位姿)静力学分析，得到水平位姿机器人系列斜面倾角应力、位移云图，部分云图如图3 所示。

图3 水平位姿机器人系列斜面倾角应力云图

分析发现，水平位姿机器人系列斜面倾角的最大位移均发生于末端执行器上，变形范围为0.804 ～1.04 mm;最大应力均发生于斜面滑块上，θ =25°时整机所受最大应力最小，为68.2 MPa，但这个值不一定最优。接着在θ =25°附近利用“最小二乘法”理论，相隔0.5°建立一个结构简化模型，进行有限元分析，逐步逼近最优值，进而找到最优解(精度控制为0.5°)。

通过综合分析，最终找到机器人水平位姿斜面最优倾角θ =26°，此时最大应力66.9 MPa，出现在大臂与腰部滑块接触端。水平位姿最大应力、位移出现位置及随斜面倾角变化趋势如图4 所示。

图4 水平位姿最大应力位移出现位置、随斜面倾角变化趋势

2.2 竖直位姿情况下不同倾角的有限元分析

同理，通过类似分析可得竖直位姿的码垛机器人斜面处于不同倾角时整机以及各部件受力的具体情况，进而找到最大应力以及最大位移发生处以及相对应的应力随倾角变化的趋势。分析发现，竖直位姿机器人系列斜面倾角最大位移均发生于末端执行器上，变形范围0.734 ～0.819 mm，θ =25°时整机所受最大应力最小，为49.2 MPa，但这个值不一定最优。接着在θ =25°附近利用“最小二乘法”理论，相隔0.5°建立一个结构简化模型，进行有限元分析，逐步逼近最优值，进而找到最优解(精度为0.5°)。通过综合分析，最终找到机器人水平位姿斜面最优倾角θ=25.5°，此时最大应力48.9 MPa，出现在小臂上。竖直位姿最大应力随斜面倾角变化趋势如图5 所示。

图5 竖直位姿最大应力位移出现位置、随斜面倾角变化趋势

2.3 斜面码垛机器人最优倾角的选取

综合上述分析可得，机器人水平位姿斜面最优倾角θ =26°，此时最大应力66.9 MPa，出现在斜面滑块上;竖直位姿斜面最优倾角θ =25.5°，此时最大应力48.9 MPa，出现在小臂上。水平位姿所受最大应力为竖直位姿的1.37 倍，作用效果更明显，优选考虑水平位姿的应力状态，故最优斜面倾角取θ =26°。

3 机器人最优斜面倾角整机有限元分析与改进

通过选取系列斜面倾角进行整机静力学分析，已找到最优斜面倾角θ =26o。接下来，对最优斜面倾角机器人整机进行水平、竖直典型位姿的结构有限元分析及改进。图4、图5 的结果显示，斜面滑块与小臂分别为整机水平、竖直位姿的最大应力处，而末端执行器为整机最大位移处，故斜面滑块、小臂和末端执行器三者均为整机的危险部位［6］，需对结构作进一步改进。

结构改进前，斜面滑块与大臂接触面积偏小、两侧护翼比较薄弱;小臂与驱动臂接触端强度不够且小臂为实心结构，导致码垛机器人在实现高速运转—急停这个动作时产生较大的惯性力，影响机器人的定位精度及稳定性;末端执行器与平行保持架联接处强度不够，且末端执行器前端过于薄弱。因此，加筋强化斜面滑块;加厚小臂与驱动臂接触端，抽空小臂内端并加强筋;加筋强化末端执行器前端并加厚末端执行与平行保持架接触端，同时抽空力学要求不高的部位，以达到减轻质量同时增加刚度的目的。

对相应结构进行改动后，运用SolidWorks Simulation 有限元模块对整机进行静力学对比分析，根据应力、位移分布云图，在正确位置加筋或抽空。由于篇幅所限，仅给出整机结构改进前后水平位姿最大应力分布对比云图，如图6 所示。

图6 整机改进前后水平位姿最大应力分布对比云图

通过对结构的有限元分析及改进，整机水平位姿最大应力由66.9 MPa 变为58.3 MPa，最大位移由0.837 mm 变为0.792 mm;竖直位姿最大应力由49.1 MPa 变为47.6 MPa，最大位移由0.738 mm 变为0.702 mm;整机质量减轻13.2 kg。

4 结论

该码垛机器人腰部采用斜面结构形式能增大导轨有效行程、改善整机受力结构。在对系列斜面倾角(θ =15°、20°、25°、30°、35°、40°)进行择优录取的过程中，精度控制为0.5°时，得到最优斜面倾角θ=26°。运SolidWorks 的有限元模块SolidWorks Simulation对最优倾角整机进行结构有限元分析及改进，结果表明，水平位姿最大应力、最大位移分别减小12.9%、5.4%;竖直位姿最大应力、最大位移分别减小3.1%、4.9%;整机质量减轻3.8%，效果较为显著。

研究结果为工业机器人整机的设计及结构参数有限元分析及改进研究提供了一种较为有效的参考。

［1］陈祝权，梁晓合，林粤科，等．六自由度串联机器人结构设计及有限元分析优化［J］．机床与液压，2013，41(23):97－101．

［2］赵臣，王刚．我国工业机器人产业发展的现状调研报告［J］．机器人技术与用，2009(2):9－13．

［3］蔡自兴．机器人学［M］．北京:清华大学出版社，2009:122－125．

［4］楼向明，曹家鑫，梅江平，等．采用SolidWorks 的高速重载码垛机器人的静力学分析和结构优化［J］．现代制造工程，2012(10):158－161．

［5］程丽，刘玉旺，骆海涛，等．165 kg 焊接机器人有限元模态分析［J］．机械设计与制造，2012(1):147－149．

［6］赵伟，殷国富，陈航，等．基于SolidWorks 和Ansys 的机器人手臂性能分析与优化设计［J］．机器人技术，2009(12):48－49．