改进的LS－SVM数学模型的交通流量预测分析

吴一凡

(江苏食品药品职业技术学院基础教学部，江苏 淮安 223003)

引言

随着城市化规模和交通网络的日益增大，导致交通网络管理工作的繁重程度急剧上升，交通事故频发。为了保证交通资源的合理分配，高质量的交通流量预测对交通网络的规划、管理和设计具有重要的理论意义和实际价值。

雷霆［1］等人将小波变换理论和神经网络技术相结合提出一种基于小波神经网络的交通流量预测模型，通过小波变换提取交通流量的细节特征和整体特征，将提取出来的交通流量特征作为神经网络的输入，并将实际交通流量作为输出，仿真结果表明预测精度较高，但其稳定性有待于进一步提高。

Guo Wen［2］等人针对BP神经网络局部最优的问题，运用PSO算法的全局寻优的优点对BP网络进行改进，并将其应用于交通流量预测，改进后模型的预测精度和收敛速度优于传统的BP神经网络，缺点是PSO存在早熟问题，容易陷入局部最优。

刘渊［3］等人将混沌理论引入小波神经网络进行网络改进，仿真结果说明混沌小波神经网络的预测误差远远小于RBF神经网络的交通流量预测，但对小波基函数的选择和确定难度较大。

杨光［4］等人结合小波核函数的多分辨率特性，提出一种基于小波核LS-SVM的交通流量预测，通过实际数据的预测验证，说明该方法具有一定的优越性，但参数的选择需要靠经验确定。

针对交通流量数据的非平稳和非线性的特点，本文结合EMD和FOA算法对LS-SVM核参数和惩罚系数进行自适应优化，提出一种基于EFLS-SVM算法的交通流量预测模型。通过EMD提取交通流量的细节特征和趋势特征，构建出基于EFLS-SVM的交通流量预测模型的输入和输出，实现交通流量的预测，为交通网络资源的优化配置提供科学合理决策的依据。

1 果蝇优化算法

果蝇优化算法(Fruit Fly Optimization Algorithm，FOA)由潘文超［5］于2011年提出的一种全新的演化式计算方法。该算法具有控制参数少、收敛速度快和收敛精度高的优点，目前被广泛地应用于函数最优化、SVM参数优化、背包问题以及神经网络权值和阈值的优化等。

果蝇优化算法具体流程如下［5］:

(1)设置果蝇优化算法的果蝇群体大小popsize和最大迭代次数Iteration，随机初始化果蝇群体位置，初始化结果分别用X_begin和Y_begin表示。

(2)根据公式(1)和公式(2)计算果蝇个体进行寻优的随机方向和距离;

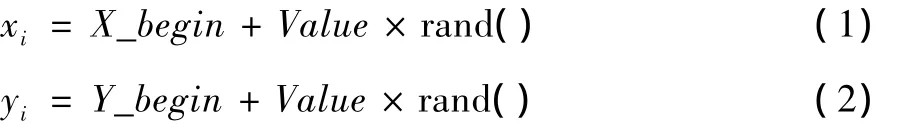
其中，Value表示果蝇的搜索距离;xi和yi分别表示果蝇个体的下一时刻的位置。

(3)根据式(3)估计果蝇个体和原点之间的距离di，之后运用式(4)计算果蝇个体的味道浓度si:

(4)味道浓度si代入式(5)味道浓度判定函数，计算出该果蝇个体当前位置的味道浓:

(5)找到果蝇群体中最佳味道浓度值和最佳位置，最佳味道浓度由Smellb表示，最佳位置由xb和yb表示。

(6)保留并记录果蝇最佳位置和最佳味道浓度，最佳味道浓度Smellbest=Smellb，果蝇初始位置X_begin=xb，Y_begin=yb，同时果蝇群体朝着该最佳位置搜寻过去。

(7)进入迭代寻优，重复迭代步骤(2)～(5)，同时判断味道浓度是否好于前一迭代味道浓度;若成立，则执行步骤(6)。

2 经验模态分解

经验模态分解吸取了小波变换多分辨的优点，同时克服了小波变换中小波基选择和分解尺度很难确定的缺点，因此EMD非常适合分析交通流量序列，因为交通流量序列是非线性、非平稳序列。

交通流量时间序列的EMD分解过程可分为［6］:

(1)识别交通流量时间序列数据中的所有极大值点，并计算拟合出其上包络线eup(t)。

(2)提取交通流量时间序列数据中的极小值点，并计算拟合出其下包络线elow(t)，在上下包络线的基础上，计算上下包络线的平均值m1(t)

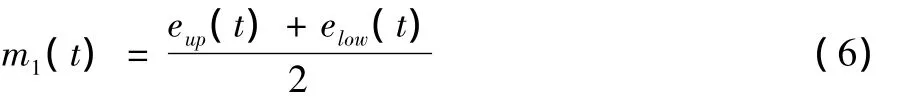
(3)将交通流量数据序列x(t)减去m1(t)，得到h1(t)，将h1(t)看成新的交通流量数据x(t)，重复步骤(1)，经过k次筛选，直至h1(t)=x(t)-1(t)满足IMF条件，令c1(t)=h1(t)，那么c1(t)则为交通流量数据的IMF1分量。

重复以上步骤，最后交通流量数据序列x(t)可被分解成为:

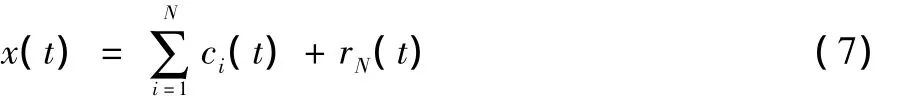
3 EFLS-SVM交通流量预测模型

3.1 LS－SVM支持向量机

Suykens提出的LS-SVM可转化为［7-8］:

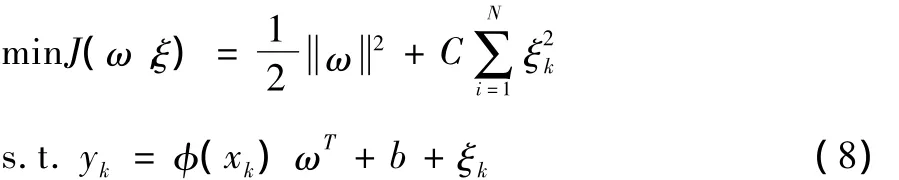
其中，ξk≥0，k=1，2，…，N，C 为惩罚因子。

通过拉格朗日法可将式(8)转化成:

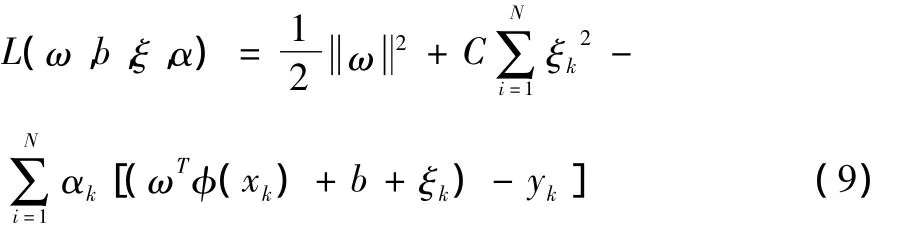
其中，αk(k=1，2，…，N)表示拉格朗日乘子。

对式(9)进行 ω、b、ξ、α 求偏导，并令其等于零，则有:

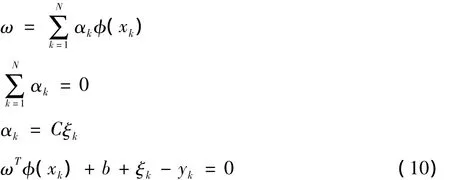
依据Mercer条件，k(xi，xj)核函数可以表示为:

本文运用RBF核函数实现预测，表达式为:

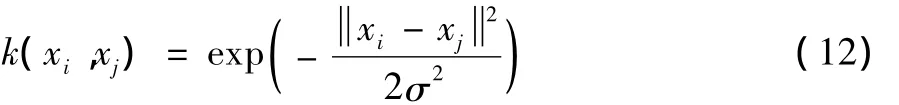
因此，LS-SVM交通流量预测模型为:

由式(13)可知，LS-SVM的性能主要受γ，σ影响，为了实现γ，σ的自适应选择，本文运用FOA算法进行γ，σ进行自适应优化。

3.2 EFLS－SVM网络预测模型

由于LS-SVM需要优化的参数为γ，σ，因此其优化的数学模型:

通过优化，在确保预测精度最优的情况下，实现γ，σ参数的自适应选择，其适应度函数可进行定义。假设t时刻的实际交通流量为y(t)，预测交通流量(t)，那么实际交通流量y(t)和预测交通流量(t)的差值e(t)公式［10］:

针对交通流量预测的非线性问题，实际交通流量数据样本为n，运用FOA优化LS-SVM的核参数和惩罚系数，使得LS-SVM的实际交通流量输出和预测交通流量之间的差值的平方和最小，适应度函数公式:

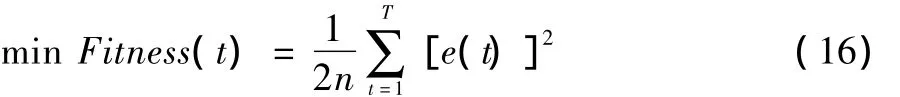
3.3 算法步骤

基于EFLS-SVM的交通流量预测流程如图1所示，算法步骤如下:

Step1:归一化交通流量数据。

Step2:EMD分解归一化的交通流量数据，提取交通流量数据的细节特征和趋势特征，构建出训练样本和测试样本。

Step3:设定FOA算法的最大迭代次数max gen，种群大小popsize。

Step 4:将构建出的训练样本输入LS-SVM，根据适应度函数式(16)计算粒子的适应度函数值，寻找粒子个体和全局最优粒子的位置和最优值。

Step 5:粒子速度和位置的更新。

Step6:计算评估适应度大小并更新粒子的位置和速度。

Step7:若gen＞max gen，保存最优解;反之gen=gen+1，转到 Step4。

Step8:根据粒子的最优位置所对应的最优参数γ，σ实现交通流量的预测。

图1 基于EFLS－SVM的预测流程图

4 仿真实验

4.1 数据来源

本文数据来源于某交通监控站监测数据，收集自2015年9月7日～21日一共15天的数据为研究对象，每天每间隔1小时采集一次车流量数据，一共采集15×24=360组数据，交通流量的原始交通流量数据及其EMD分解情况如图2所示。

4.2 数据处理

实际交通流量数据序列进行EMD分解，依次可以分解出不同的IMF分量。由图2(b)～图2(f)可知，原始交通流量数据被分解成4个波动较小的分量和1个剩余分量。根据IMF分量的分析结果，运用FOA优化LSSVM的核参数和惩罚系数的模型进行交通流量预测。

4.3 评价指标

为了验证本文算法进行交通流量预测的有效性，本文采用均方误差来评价交通流量预测效果的评价指标，评价公式:

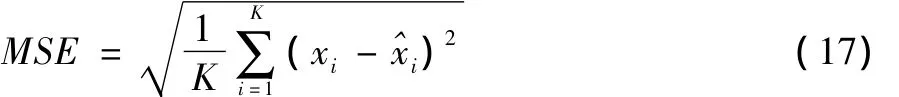
其中，xi、分别表示实际交通流量和预测交通流量。

4.4 实验结果

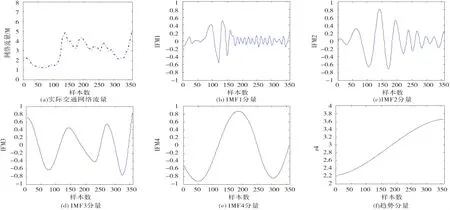
图2 实际交通流量和EMD分解结果图

将收集的360组交通流量数据分成训练样本和测试样本，将前336组数据作为训练数据，用于建立预测模型;后面24组作为测试数据，用于验证预测结果的好坏。设定FOA算法的最大迭代次数为100，种群大小为20，其预测结果如图3～图6所示，分别表示单步预测、3步预测、5预测和7步预测。

图3 基于EFLS－SVM算法的单步交通流量预测

由EFLS-SVM算法的单步预测、3步预测、5步预测和7步预测结果可知，随着预测步长的增加，EFLSSVM算法的预测精度不断提高，效果较好。图7表示FOA算法优化LS-SVM的适应度收敛曲线。

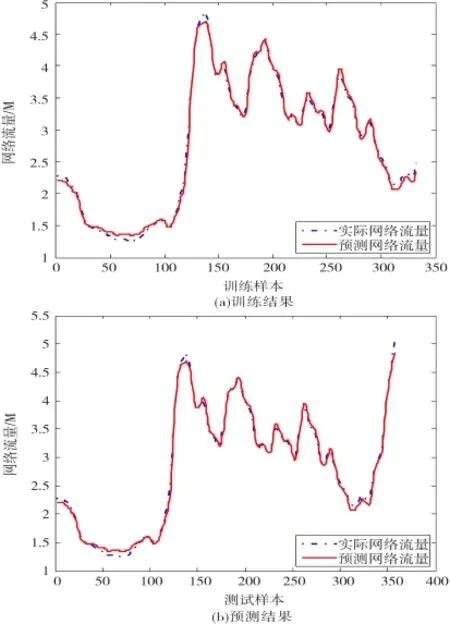
图4 基于EFLS－SVM算法的3步交通流量预测

为了验证EFLS-SVM算法的优越性，将EFLSSVM算法、FOA-LSSVM和LS-SVM三者的预测结果进行对比，运行10次，其对比结果见表1。

由表1中EFLS-SVM算法、FOA-LSSVM和LSSVM三者预测的MSE误差对比结果可知，EFLS-SVM算法的预测效果最好，优于FOA-LSSVM和LS-SVM模型，其次FOA-LSSVM的预测效果优于LS-SVM。

由表2中EFLS-SVM算法、FOA-LSSVM和LSSVM三种模型预测时间对比结果可知，EFLS-SVM算法的预测时间最短快于FOA-LSSVM和LS-SVM模型，而FOA-LSSVM的预测时间短于LSS-VM。

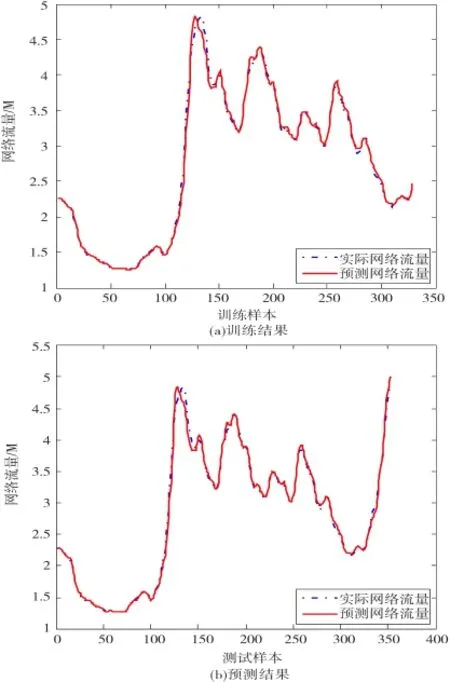
图5 基于EFLS－SVM算法的5步交通流量预测

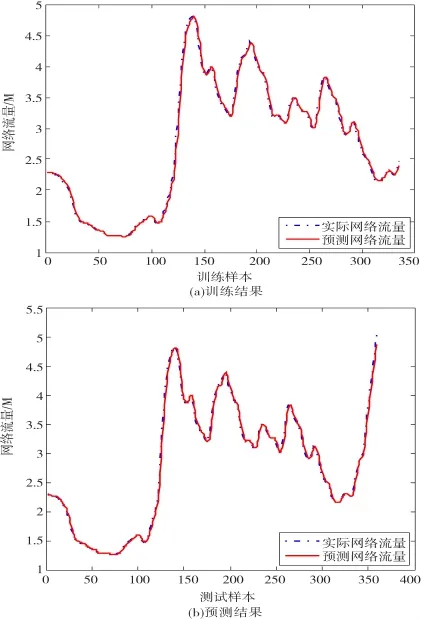
图6 基于EFLS－SVM算法的7步交通流量预测

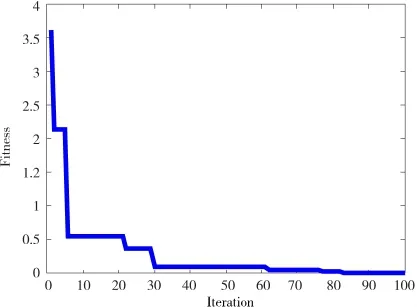
图7 FOA优化LS－SVM的适应度收敛曲线图

表1 EFLS－SVM算法、FOA－LSSVM和LS－SVM三种模型预测MSE误差对比

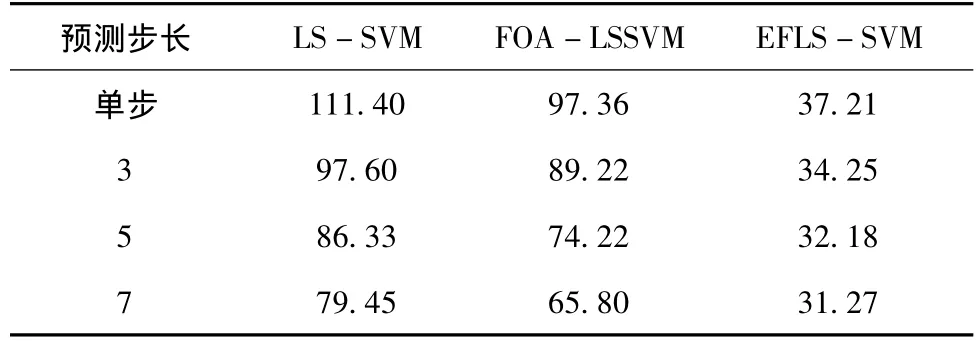
表2 EFLS－SVM算法、FOA－LSSVM和LSSVM三种模型预测时间对比(单位:s)

为了进一步验证本文算法的有效性和可靠性，选择CUDA标准测试数据库为研究对象［11-12］，进行交通流量预测。将前276组数据作为训练数据，后面92组作为测试数据。设定FOA算法的最大迭代次数为100，种群大小为20，其预测结果如图8所示。

由图8可知，本文算法的预测精度较高，预测平均相对误差6.71%，可以进行实际交通流量预测，不过存在个别点预测精度较低的缺点，可能受到其他影响因素的制约，如算法的性能、交通流量实际影响因素等。

图8 CUDA标准数据集预测结果

5 结束语

针对LS-SVM核参数和惩罚系数选择的随机性，本文运用FOA算法对LS-SVM核参数和惩罚系数进行优化，同时结合EMD提取交通网络流量的细节特征和趋势特征，构建出基于EFLS-SVM的交通网络流量预测模型，分别进行单步、3步、5步和7步预测。通过对不同交通网络流量预测模型预测均方误差和预测时间发现，EFLS-SVM算法的预测精度和预测效率均优于其他模型，从而为交通网络资源的合理配置提供科学决策的依据。

[1] 雷霆,余镇危.一种交通流量预测的小波神经网络模型[J].计算机应用,2012,26(3):526-528.

[2] Guo Wen,Qiao Yizheng,Hou Haiyan.BP neural network optimized with PSO algorithm and its application in forecasting[C]//Proceedings of the IEEE international Conference on Information Acquisition,Weihai,China,January 1,2011:617-621.

[3] 刘渊,戴悦,曹建华.基于小波神经网络的流量混沌时间序列预测[J].计算机工程,2012,34(16):105-110.

[4] 杨光,张国梅,刘星宇.基于小波核LS-SVM的交通流量预测[J].微机发展,2011,15(12):125-128.

[5] Pan W T.A new fruit fly optimization algorithm:Taking the financial distress model as an example[J].Knowledge-Based Systems,2012,26:69-74.

[6] 王西锋,高岭,张晓孪.自相似交通网络流量预测的分析和研究[J].计算机技术与发展,2010,17(11):42-45.

[7] 冯海亮,林青家,陈涤,等.一种基于神经网络的交通网络流量组合预测模型[J].计算机应用,2010,26(9):2206-2208.

[8] Cervellera C,Wen A H,Chen V C P.Neural network and regression spline value function approximations for stochastic dynamic programming[J].Computer&Operations Research,2012,34(1):70-90.

[9] Li Junfeng,Yang Aiping,Dai Wenzhan.Modeling mechanism of Grey Neural Network and its application[C]//Proceedings of 2007 IEEE International Conference on Grey Systems and Intelligent Services,Nanjing,November 18-20,2009:404-408.

[10] 李宗福,邓琼波,李桓.Kohonen SOFM神经网络及其演化研究[J].计算机工程与设计,2013,25(10):1729-1830.

[11] Wang H,Liu Y,Zeng S Y.A Hybrid Particle Swarm Algorithm with Cauchy Mutation[C]//Proceeding of IEEE Swarm Intelligence Symposium(SIS),Honolulu,HI,April 1-5,2011:356-360.

[12] Wang H,Liu Y,Wu Z,et al.An improved particle swarm optimization with adaptive jumps[C]//Proceedings of IEEE International Conference on Evolutionary Computation,Brisbane,Australia,June 10-15,2012:392-397.